Изобретение относится к области волоконно-оптической связи, в частности к оптимизации параметров DWDM (Dense Wavelength Division Multiplexing -плотное мультиплексирование с разделением по длине волны) систем терабитного класса в гетерогенных ВОЛС (волоконно-оптические линии связи).
Из уровня техники известен способ оптимизации параметров DWDM систем связи путем численного решения нелинейных волновых уравнений для распространения световых сигналов, вариации мощности на выходе передатчика и коэффициентов усиления усилителей, построение зависимостей параметров качества (Q-фактора) от мощности передатчика и коэффициентов усиления усилителя и нахождении оптимальных параметров, обеспечивающих максимальную дальность работы системы связи (Редюк А.А. и др., Математическое моделирование экспериментального прототипа высокоскоростной линии связи на основе дифференциального фазового формата модуляции без возвращения к нулю. Квантовая электроника. 2011. Т. 41. № 10. с. 929-933).
Основной недостаток известного технического решения состоит в огромном объеме вычислений, которые нужно провести для его реализации. Объем вычислений особенно сильно возрастает при оптимизации DWDM систем терабитного класса в мультиформатных гетерогенных ВОЛС, что делает его неприменимым для проведения практической оптимизации проектных решений.
Наиболее близким к заявленному техническому решению - прототипом -является способ оптимизации параметров DWDM систем терабитного класса в гетерогенных волоконно-оптических линиях связи (ВОЛС), содержащих передатчик, многопролетную ВОЛС из N пролетов, где N - целое число не менее 2, в конце каждого из которых за исключением последнего расположен линейный оптический усилитель, и приемник, заключающийся в измерении потерь в каждом из пролетов и установку вычисленных с учетом измеренных потерь оптимальной мощности сигналов на выходе передатчика P и оптимальных коэффициентов усиления gk линейных оптических усилителей (Трещиков В.Н., Листвин В.Н. DWDM-системы, 4-е издание. М.: ТЕХНОСФЕРА. 2021. с. 383-397). В отличие от аналога, прототип позволяет существенно уменьшить количество вычислений.
К недостаткам прототипа следует отнести область его применения, ограниченную системами передачи информации с периодической компенсацией дисперсии, тогда как в волоконно-оптических системах передачи информации без периодической компенсации дисперсии кардинально меняется характер распространения оптических сигналов и характер нелинейных искажений. Нелинейные искажения оптического сигнала в многопролетных когерентных ВОЛС с большой канальной скоростью (терабитного класса) можно описать как формирование нелинейного интерференционного шума. Такие линии связи без компенсации дисперсии на физическом уровне были ранее исследованы авторами (V.A. Konyshev et al. Accumulation of nonlinear noise in coherent communication lines without dispersion compensation. Optics Communications, Volume 349, 15 August 2015, Pages 19-23), введена функция корреляции нелинейных шумов последовательных пролетов и экспериментально измерены зависимости функции корреляции от разности накопленных дисперсий на входах в пролеты. Обнаружено, что при определенных условиях коэффициент корреляция уменьшается и становится меньше 1. Это означает, что нелинейные шумы от соседних пролетов частично компенсируют друг друга.
С учетом изложенного проблему, решаемую заявленным техническим решением, можно охарактеризовать, как обеспечение учета декорреляции нелинейных шумов при оптимизации параметров DWDM систем терабитного класса в мультиформатных гетерогенных ВОЛС.
Технический результат состоит в расширении области применения способа оптимизации параметров DWDM систем терабитного класса в мультиформатных гетерогенных ВОЛС за счет его применимости в системах передачи информации без периодической компенсации дисперсии.
Проблема решается, а заявленный технический результат достигается тем, что в способе оптимизации параметров DWDM систем терабитного класса в гетерогенных ВОЛС, содержащих передатчик, многопролетную ВОЛС из N пролетов, где N целое число не менее 2, в конце каждого из которых за исключением последнего расположен линейный оптический усилитель, и приемник, заключающемся в измерении потерь в каждом из пролетов и установку вычисленных с учетом измеренных потерь оптимальной мощности сигналов на выходе передатчика P и оптимальных коэффициентов усиления gk линейных оптических усилителей, дополнительно определяют коэффициент корреляции нелинейных шумов линии ε и коэффициенты нелинейности пролетов ηk а оптимальные значение мощности сигналов на выходе передатчика Р и коэффициентов усиления gk вычисляют согласно следующему:
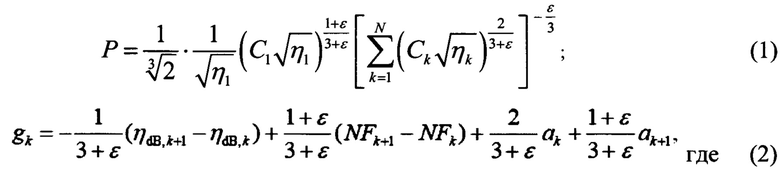
k - номер пролета от 1 до N;
Ck=AM⋅hvBAkFk - введенный расчетный коэффициент;
AM - эксплуатационный запас по OSNR;
h - постоянная Планка;
v - несущая частота;
B - референсная частота;
Ak - потери мощности сигнала в k-том пролете;
Fk - шум-фактор усилителя, расположенного в конце k-го пролета;
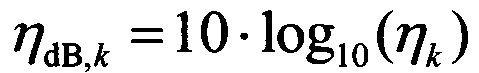 - коэффициент нелинейности k-го пролета в децибельном представлении;
- коэффициент нелинейности k-го пролета в децибельном представлении;
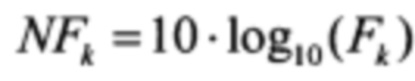 - шум-фактор усилителя, расположенного в конце k-го пролета, в децибельном представлении;
- шум-фактор усилителя, расположенного в конце k-го пролета, в децибельном представлении;
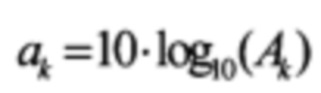 - потери мощности сигнала в k-том пролете в децибельном представлении.
- потери мощности сигнала в k-том пролете в децибельном представлении.
Вычисленные по формулам (1) и (2) оптимальное значение мощности сигнала на выходе передатчика P и оптимальные коэффициенты усиления линейных оптических усилителей gk обеспечивают максимальную дальность с сохранением работоспособности ВОЛС для любого значения коэффициента корреляции е, который в разных ВОЛС может изменяться от 1 до 0. Это существенно увеличивает область применения предлагаемого способа по сравнению со способом оптимизации, описанным в прототипе, который пригоден для оптимизации только ВОЛС с компенсацией дисперсии, в которых ε=1. Изобретение поясняется изображениями, где:
- на Фиг. 1 схематично показана многопролетная DWDM система терабитного класса;
- на Фиг. 2 представлены зависимости диапазона допустимых входных канальных мощностей DWDM сигнала от длины многопролетной линии с периодической компенсацией дисперсии и без компенсации дисперсии (закрашена область допустимых входных мощностей);
- на Фиг. 3 представлена диаграмма усиления для k-го пролета;
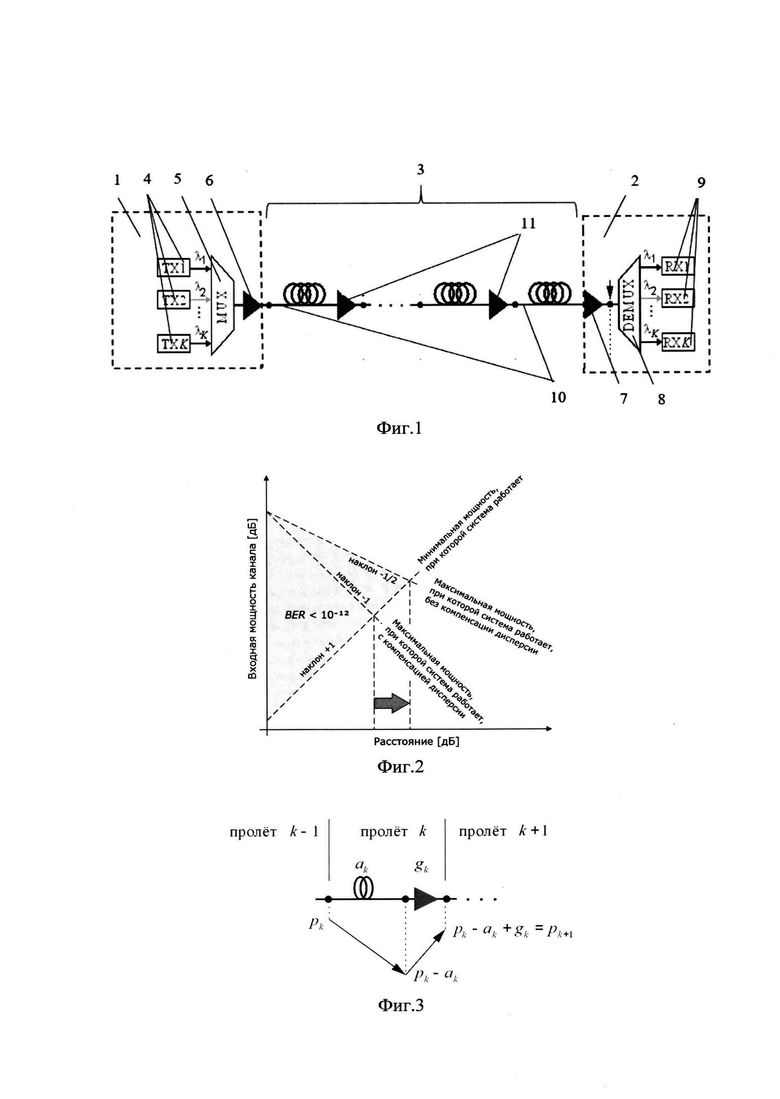
- на Фиг. 4 представлена зависимость числа пролетов от мощности, вводимой в пролеты (линия состоит из одинаковых пролетов длиной 100 км, километрическим затуханием 0.2 дБ/км, шум-факторы усилителей 5 дБ, коэффициент нелинейности пролета 140 Вт-2), коэффициент корреляции нелинейных шумов линии ε=0.5, OSNRBTB=12дБ, в отсутствии эксплуатационного запаса (AM=1);
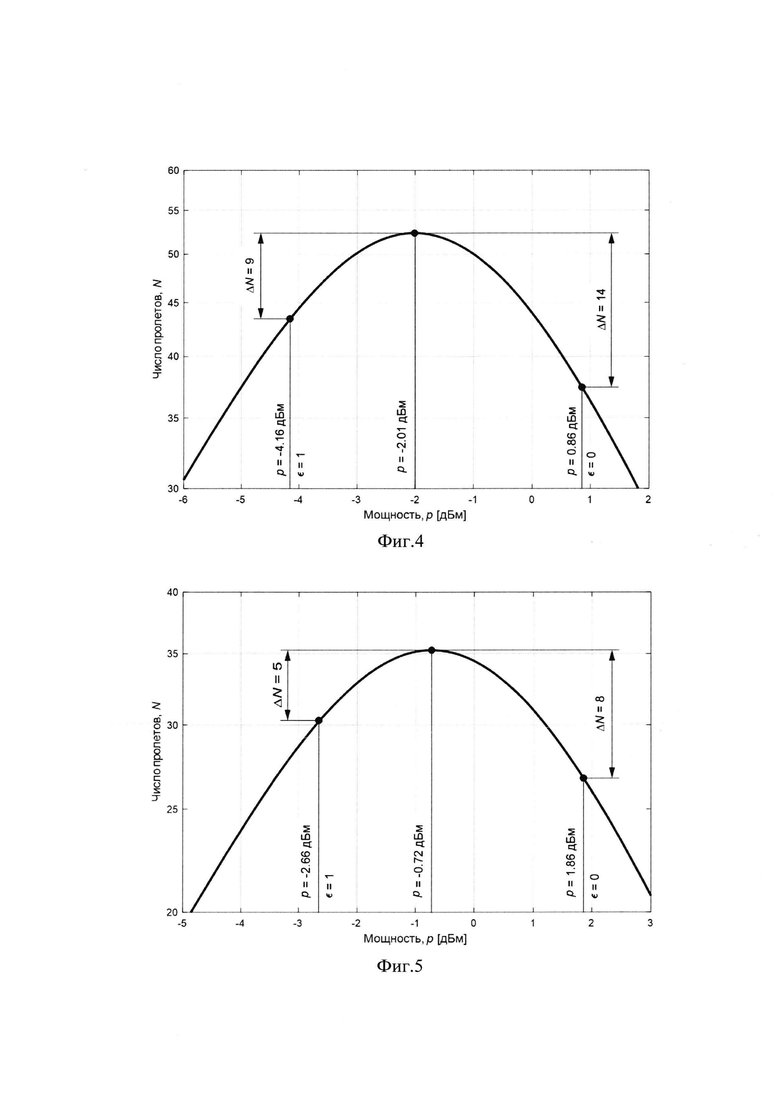
- на Фиг. 5 представлена зависимость числа пролетов от мощности, вводимой в пролеты (линия состоит из одинаковых пролетов длиной 100 км, километрическим затуханием 0.2 дБ/км, шум-факторы усилителей 5 дБ, коэффициент нелинейности пролета 140 Вт-2), коэффициент корреляции нелинейных шумов линии ε=0.5, OSNRBTB=12дБ, при наличии эксплуатационного запаса (AM=2).
Цифровые позиции, указанные на изображениях, означают следующее:
1 - передатчик;
2 - приемник;
3 - волоконно-оптическая линия связи (ВОЛС);
4 - передатчики абонентов;
5 - мультиплексор;
6 - усилитель передающего модуля (бустер);
7 - усилитель принимающего модуля;
8 - демультиплексор;
9 - приемники абонентов;
10 - пролеты;
11 - линейные оптические усилители.
Изобретение основано на следующем. Проведенные экспериментальные и теоретические исследования показали, что в линиях без оптической компенсации дисперсии накопление нелинейных искажений происходит значительно медленнее, чем в традиционных линиях связи с периодической компенсацией дисперсии. Это приводит к тому, что длина многопролетных линий связи без периодической компенсации дисперсии может быть значительно больше длины традиционных линий. Принципиальная схема стандартной многопролетной линии связи представлена на Фиг. 1, носит исключительно иллюстрирующий характер и дополнительных пояснений не требует. На Фиг. 2 показаны зависимости диапазона допустимых входных канальных мощностей DWDM - сигнала от длины многопролетной линии. Более медленный рост величины нелинейного штрафа при увеличении длины линии без компенсации дисперсии объясняется изменением характера нелинейных искажений. В длинных линиях нелинейные эффекты проявляются в форме нелинейных шумов. В этом случае работу системы связи можно описать простой корректировкой выражения для OSNR (Optical Signal to Noise Ratio - отношение оптического сигнала к шуму):

Как следует из формулы (3) избыточный нелинейный шум мощностью PNL суммируется с шумом PASE усиленного спонтанного излучения. Коэффициент ошибок BER зависит от скорректированного OSNR также, как в линейном режиме от 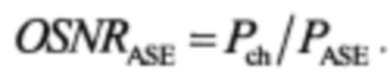 В традиционных линиях с компенсацией дисперсии нелинейный штраф растет быстро, т.к. шумы складываются когерентно (коэффициент корреляции ε=1). В линиях без компенсации дисперсии или с частичной компенсацией дисперсии нелинейный штраф растет медленнее, т.к.
В традиционных линиях с компенсацией дисперсии нелинейный штраф растет быстро, т.к. шумы складываются когерентно (коэффициент корреляции ε=1). В линиях без компенсации дисперсии или с частичной компенсацией дисперсии нелинейный штраф растет медленнее, т.к.
коэффициент корреляции шумов от разных пролетов уменьшается (становится меньше 1).
Установлено, что в линиях без компенсации дисперсии (или с частичной компенсацией), характеризующихся определенным значением ε, возможна оптимизация мощности сигналов Р на выходе передатчика 1 и оптимальных коэффициентов усиления gk линейных оптических усилителей 11 по формулам (1) и (2). Поскольку полученные значения Р и gk зависят от ε, значение коэффициента корреляции нелинейных шумов линии ^ (в интервале от 0 до 1) должно быть измерено или рассчитано. Расчет коэффициентов корреляции нелинейных шумов линии s (равно, как и коэффициент нелинейности пролетов ηk) не является предметом настоящего изобретения и подробно не рассматривается, поскольку может быть произведен с использованием известных методик (см., например, P. Poggiolini et al, The GN-Model of Fiber Non-Linear Propagation and its Applications, JOURNAL OF LIGHTWAVE TECHNOLOGY, VOL. 32, NO. 4, FEBRUARY 15, 2014, c.694 - 721).
Максимальная дальность достигается при достижении максимума OSNR, то есть при достижении минимума обратного OSNR, имеющего вид
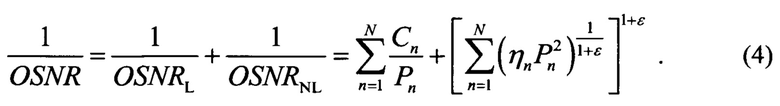
где коэффициенты Cn определены при описании формулы (1) с учетом запаса по OSNR, как это делается при проектировании.
Максимум OSNR достигается при значениях мощностей Р1,Р2,…,PN, таких, что выражение (4) достигает минимума. Для их нахождения сделаем замену переменных

Тогда выражение (4) примет вид: 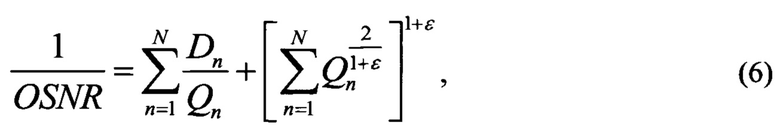
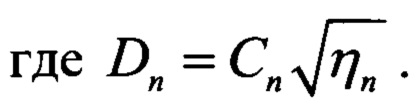
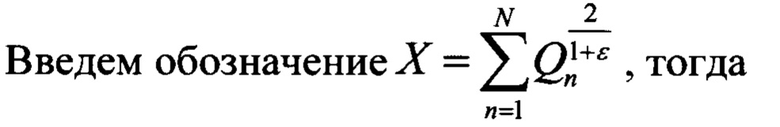

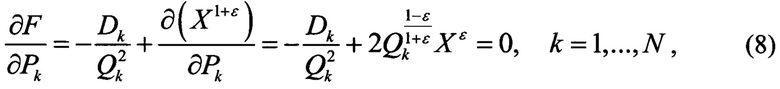
или 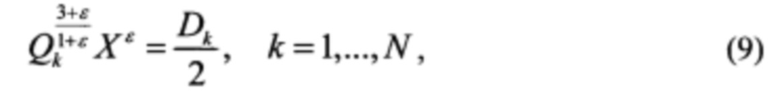
или
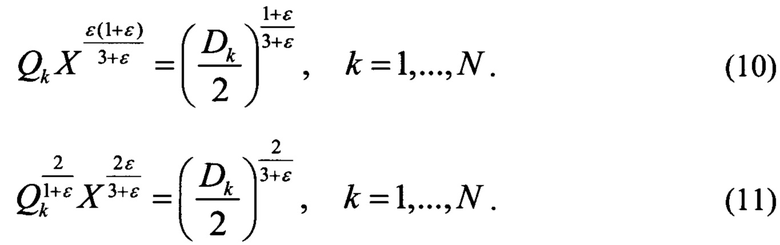
Просуммировав (11) по k;, получаем или или 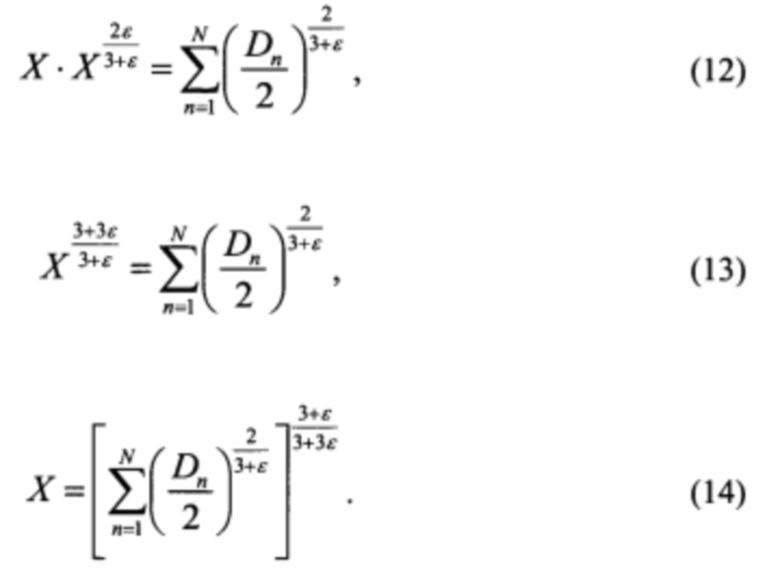
подставляя.X в (10), получаем: 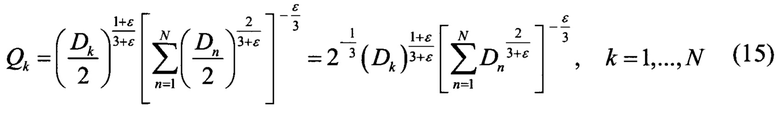
и с учетом соотношения (5) получаем формулу для мощностей, вводимых в каждый пролет
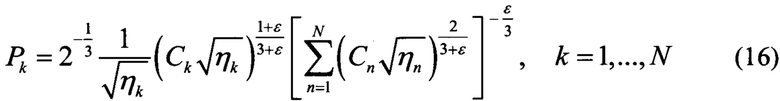
Мощность, вводимая в первый пролет (k=1) совпадает с формулой (1). Мощности, вводимые во второй и следующие пролеты устанавливаются путем выбора оптимальных коэффициентов усиления gk линейных усилителей. С использованием соотношения gk=pk+1 - pK+aK, связывающего коэффициенты усиления gk линейных усилителей, потери в пролетах и мощности на входе в пролеты pk(см. Фиг. 3) получаем формулу (2).
Если волокна в пролетах одного типа и длины пролетов больше чем Leff, то нелинейные коэффициенты пролетов одинаковые η1=η2=…ηN=η. Также если допустить, что шум-факторы усилителей одинаковые NF1=NF2=…=NFN, формула (2) принимает вид:
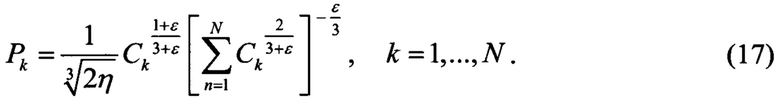
в децибельном представлении:
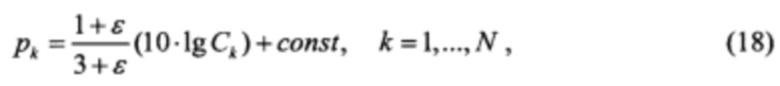
или
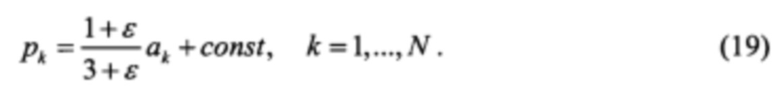
Примеры реализации заявленного способа моделировались в DWDM системе терабитного класса мультиформатной гетерогенной ВОЛС на основе оборудования «Волга» компании Т8. Исходные параметры:
ε - коэффициент корреляции (ε=0.5 [относительных единиц]);
ηk - коэффициент нелинейности пролета (ηk=140 [Вт-2]);
h - постоянная Планка (h=6.626 -10-34 [Вт х с2]);
v - несущая частота (v=193.1-1012 [Гц]);
Β -референсная частота (Β=12.5⋅109[Гц]);
α - километрическое затухание в пролете (α=0.2 [дБ/км]);
Результаты реализаций наглядно представлены на Фиг. 4 и Фиг. 5.
На Фиг. 4 показано, что в отсутствии запаса (AM=1) при оптимизации ВОЛС предложенным способом дальность работы системы связи увеличивается на 900 км по сравнению с дальностью, получаемой при оптимизации по способу, описанному в прототипе. Также показано, что при оптимизации ВОЛС предложенным способом дальность работы системы связи увеличивается на 1400 км по сравнению с дальностью, получаемой при оптимизации по способу, соответствующему отсутствию корреляции шумов соседних пролетов. Изложенное свидетельствует, что заявленным способом оптимум достигнут однозначно, а результаты, полученные по прототипу, оптимумом для систем передачи информации без периодической компенсации дисперсии не являются.
Аналогично, на Фиг. 5 показано, что при запасе AM=2 при оптимизации ВОЛС предложенным способом дальность работы системы связи увеличивается на 500 км по сравнению с дальностью, получаемой при оптимизации по способу, описанному в прототипе. Также показано, что при оптимизации ВОЛС предложенным способом дальность работы системы связи увеличивается на 800 км по сравнению с дальностью, получаемой при оптимизации по способу, соответствующему отсутствию корреляции шумов соседних пролетов. Изложенное свидетельствует, что заявленным способом оптимум достигнут однозначно, а результаты, полученные по прототипу, оптимумом для систем передачи информации без периодической компенсации дисперсии не являются.
Изложенное позволяет сделать вывод о том, что выявленная проблема - обеспечение учета корреляции нелинейных шумов при оптимизации параметров DWDM систем терабитного класса в мультиформатных гетерогенных ВОЛС -решена, а заявленный технический результат - расширение области применения способа оптимизации параметров DWDM систем терабитного класса в мультиформатных гетерогенных ВОЛС за счет его применимости в системах передачи информации без периодической компенсации дисперсии - достигнут.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОНТРОЛЯ СИСТЕМОГО ЗАПАСА ПО ОТНОШЕНИЮ ОПТИЧЕСКИЙ СИГНАЛ/ШУМ И КОГЕРЕНТНОЕ ПРИЕМНОЕ УСТРОЙСТВО | 2015 |
|
RU2677263C2 |
| ВОЛОКОННО-ОПТИЧЕСКАЯ СИСТЕМА СВЯЗИ | 2014 |
|
RU2572363C1 |
| ВОЛОКОННО-ОПТИЧЕСКАЯ СИСТЕМА СВЯЗИ | 2014 |
|
RU2576667C1 |
| Способ измерения запаса по OSNR в линии связи со спектральным уплотнением DWDM и кодированием сигнала с исправлением ошибок FEC | 2017 |
|
RU2695775C1 |
| ЛОГАРИФМИЧЕСКИЙ КОНТРОЛЛЕР ЗАЩИТЫ МНОГОПРОЛЕТНЫХ ВОЛОКОННО-ОПТИЧЕСКИХ ЛИНИЙ | 2016 |
|
RU2617726C1 |
| ВЫСОКОСКОРОСТНАЯ ОПТИЧЕСКАЯ ЛИНИЯ, ЗАЩИЩЕННАЯ ОТ ПРОСЛУШИВАНИЯ КВАНТОВЫМ ШУМОМ | 2012 |
|
RU2520419C1 |
| СПОСОБ КОНТРОЛЯ ФУНКЦИОНИРОВАНИЯ КАНАЛОВ И СИСТЕМА ОПТИЧЕСКОЙ СВЯЗИ | 2016 |
|
RU2696560C2 |
| УСТРОЙСТВО ДЛЯ СТАБИЛИЗАЦИИ ФАЗЫ ПЕРЕДАВАЕМОГО ПО ВОЛС ВЫСОКОЧАСТОТНОГО АНАЛОГОВОГО СИГНАЛА | 1997 |
|
RU2119719C1 |
| ЦИФРОАНАЛОГОВЫЙ ПРЕОБРАЗОВАТЕЛЬ С ЛИНИЕЙ ПЕРЕДАЧИ | 2010 |
|
RU2420866C1 |
| Однопролетная волоконно-оптическая линия связи | 2024 |
|
RU2841363C1 |
Изобретение относится к области волоконно-оптической связи. Технический результат состоит в увеличении дальности с сохранением работоспособности ВОЛС (волоконно-оптические линии связи), что расширяет область применения способа оптимизации параметров DWDM (Dense Wavelength Division Multiplexing – плотное мультиплексирование с разделением по длине волны) систем терабитного класса в гетерогенных ВОЛС, который может применяться в системах передачи информации без периодической компенсации дисперсии. Технический результат достигается тем, что в способе оптимизации параметров DWDM-систем терабитного класса в гетерогенных ВОЛС, содержащих передатчик 1, многопролетную ВОЛС 2 из N пролетов 10, где N – целое число не менее 2, в конце каждого из которых за исключением последнего расположен линейный оптический усилитель 11, и приемник 2, измеряют потери в каждом из пролетов и устанавливают вычисленные с учетом измеренных потерь оптимальной мощности сигналов на выходе передатчика Р и оптимальных коэффициентов усиления gk линейных оптических усилителей, причем оптимальные значения мощности сигналов на выходе передатчика Р и коэффициентов усиления gk вычисляют с использованием дополнительно определенных коэффициента корреляции нелинейных шумов линии ε и коэффициентов нелинейности пролетов ηk. 5 ил.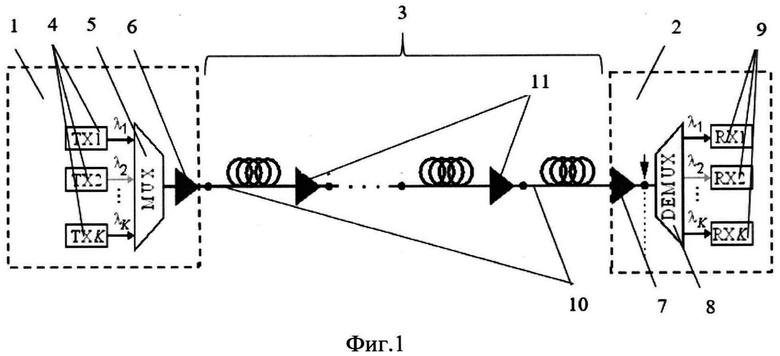
Способ оптимизации параметров DWDM систем терабитного класса в гетерогенных ВОЛС, содержащих передатчик, многопролетную ВОЛС из N пролетов, где N - целое число не менее 2, в конце каждого из которых за исключением последнего расположен линейный оптический усилитель, и приемник, заключающийся в измерении потерь в каждом из пролетов и установку вычисленных с учетом измеренных потерь оптимальной мощности сигналов на выходе передатчика Р и оптимальных коэффициентов усиления gk линейных оптических усилителей, отличающийся тем, что дополнительно определяют коэффициент корреляции нелинейных шумов линии и коэффициенты нелинейности пролетов ηk а оптимальные значение мощности сигналов на выходе передатчика Р и коэффициентов усиления gk вычисляют согласно следующему:
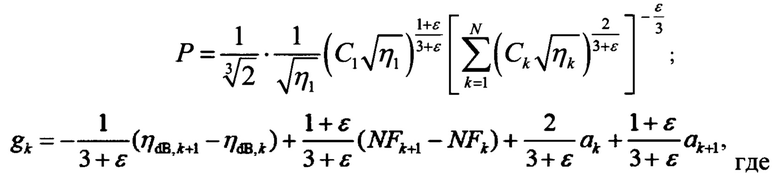
k - номер пролета от 1 до N;
Ck=AM⋅hνBAkFk - введенный расчетный коэффициент;
AM - эксплуатационный запас по OSNR;
h - постоянная Планка;
ν - несущая частота;
B - референсная частота;
Ak - потери мощности сигнала в k-м пролете;
Fk - шум-фактор усилителя, расположенного в конце k-го пролета;
ndB,k=10⋅log10(ηk) - коэффициент нелинейности k-го пролета в децибельном представлении;
NFk=10⋅log10(Fk) - шум-фактор усилителя, расположенного в конце k-го пролета, в децибельном представлении;
a k=10⋅log10(Ak) - потери мощности сигнала в k-м пролете в децибельном представлении.
| Трещиков В.Н., Листвин В.Н | |||
| DWDM-системы, 4-е издание | |||
| М.: ТЕХНОСФЕРА | |||
| Способ регенерирования сульфо-кислот, употребленных при гидролизе жиров | 1924 |
|
SU2021A1 |
| Передвижная комнатная печь | 1922 |
|
SU383A1 |
| US8055129 B2, 08.11.2011 | |||
| US20150304035 A1, 22.10.2015 | |||
| CN110336609 A, 15.10.2019 | |||
| US9413455 B2, 09.08.2016 | |||
| US20110038627 A1, 17.02.2011 | |||
| US9002200 B2, 07.04.2015 | |||
| CN114124214 B, 17.02.2023 | |||
| Р.Ибрагимов и др: "Зависимость пропускной способности DWDM-линий с | |||
Авторы
Даты
2024-03-28—Публикация
2023-06-14—Подача