Изобретение относится к способам и устройствам для анализа ионов по энергиям, массам, зарядам с использованием электрических и магнитных полей и расчетам по результатам анализа плотности ионов плазмы и может быть использовано для определения характеристик, например, потоков плазмы рабочего вещества технологических ускорителей плазмы и плазменных двигателей.
Известен способ измерения плотности положительно заряженных ионов с помощью электрического зонда (зонда Ленгмюра) [Langmuir I. and Mott-Smith H. Studies of Electric Discharges in Gases at Low Pressures. Part I // General Electric Review, 1924. - V. 27, No. 7. - P. 449-455; Шотт Л. Электрические зонды. - В кн. Методы исследования параметров плазмы / Под ред. В. Лохте-Хольтгревена, М.: Мир, 1971. - 552 с.; Козлов О.В. Электрический зонд в плазме // М.: Атомиздат, 1969. - 291 с.].
Известный способ реализуется следующим образом:
1) электрический зонд заданной конфигурации (плоский, цилиндрический или сферический) помещают в область плазмы, где нужно определить плотность ионов;
2) от внешнего источника постоянного тока подают на зонд отрицательный потенциал;
3) изменяют величину потенциала до тех пор, пока ионный ток на зонд перестает изменяться - достигается его максимальное значение - ток насыщения Iis;
4) вычисляют плотность ионов из формулы для ионного тока насыщения на плоский зонд:
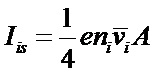 ,
,
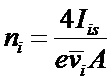 ,
,
где
е - заряд электрона,
ni - плотность ионов в предположении квазинейтральной плазмы, когда плотность ионов ni равна плотности электронов ne,
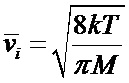 - средняя скорость ионов,
- средняя скорость ионов,
Т - температура ионов,
Mi - масса иона;
k - постоянная Больцмана;
А - площадь поверхности зонда.
Признаками известного способа, совпадающими с существенными признаками заявляемого способа, являются:
1) вычисляют плотность ионов.
Недостатками известного способа являются:
1) зонд помещается в плазму, что приводит к эмиссии заряженных частиц с поверхности зонда и, как следствие, к изменению тока на зонд - погрешности измерения плотности ионов;
2) ток на зонд в плазме с магнитным полем зависит от ориентации собирающей поверхности зонда относительно направления магнитного поля;
3) плотность ионов измеряется косвенным методом: по ионному току насыщения на зонд Iis; измерив Iis, плотность ионов рассчитывается по формуле
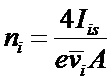 ;
;
для расчета ni необходимо независимым способом измерить температуру ионов Т, которая определяет среднюю скорость 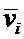 :
:
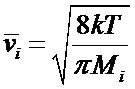 ;
;
4) в случае многокомпонентной плазмы масса ионов Mi становится неопределенной, поэтому необходимо независимо определять парциальный вклад ионов разных масс, вводить понятие эффективной массы Meff.
Известен способ измерения плотности ионов [Patent No.: US 11,735,397 B2. Hyo Chang Lee, Jung Hyung Kim, Hee Jung Yeon. Device for measuring plasma ion density and apparatus for diagnosing plasma using the same].
Известный способ реализуется следующим образом:
1) приемо-передающие антенны выбранной конструкции размещают в области плазмы, где нужно определить плотность ионов;
2) включают микроволновой генератор электромагнитных колебаний и изменяют его частоту, например, в диапазоне 100 кГц - 500 МГц;
3) регистрируют сигнал приемной антенной и выделяют частоту отсечки fcut-off - частоту, при которой плазма перестает быть прозрачной для излучения и сигнал на приемную антенну резко падает по амплитуде;
4) конвертируют значение частоты отсечки в плотность ионов, используя соотношения:
fcut
-
off
= fpi = 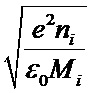 ,
,
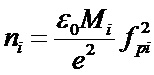 ,
,
где
fpi - ионная плазменная частота;
ε 0 - диэлектрическая постоянная;
Mi - масса иона плазмообразующего (рабочего) газа.
Признаками известного способа, совпадающими с существенными признаками заявляемого способа, являются:
1) вычисляют плотность ионов.
Недостатками известного способа являются:
1) плотность ионов измеряется косвенным методом: по ионной плазменной частоте fpi; 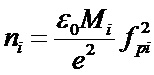 ;
;
2) в случае многокомпонентной плазмы масса ионов Mi в формуле
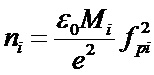
становится неопределенной, поэтому необходимо независимо определять парциальный вклад ионов разных масс, вводить понятие эффективной массы Meff.
Известен способ измерения плотности положительно заряженных ионов [Афросимов В.В. Методы корпускулярной диагностики высокотемпературной плазмы / В кн. Диагностика плазмы. Выпуск 3. М.: Атомиздат, 1973. - 560 с.; Tokamak plasma diagnostics. Equipe TFR // Nuclear Fusion, 1978. - V. 18, No. 5. - Р. 647-731; Никишин А.В., Иванов И.А., Баткин В.И., Бурдаков А.В., Куклин К.Н., Меклер К.И., Поступаев В.В., Ровенских А.Ф. Многохордовая пучковая диагностика плазмы на установке ГОЛ-NB // Физика плазмы, 2022. - Т. 48, №3. - С. 212-221].
Известный способ реализуется следующим образом:
1) создают диагностический пучок нейтральных частиц требуемого типа и энергии;
2) пропускают пучок через плазму с линейным размером l;
3) регистрируют прошедший через плазму пучок нейтралов;
4) определяют отношение плотности тока J ослабленного пучка к плотности тока J0 исходного пучка;
5) определяют линейную плотность ионов nl, используя соотношение
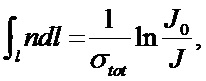
где
σtot - полное сечение потерь частиц диагностического пучка;
6) зная длину l взаимодействия пучка с плазмой, определяют плотность ионов n.
Недостатками известного способа являются:
1) За ослабление моноэнергетического пучка атомов, пересекающего плазму, ответственны следующие процессы:
- обмен зарядом с ионами плазмы;
- ионизация ионами плазмы;
- ионизация электронами плазмы;
- упругое рассеяние на ионах и электрона плазмы и нейтральным газом;
- обдирка на нейтральном газе;
- обмен зарядом и ионизация примесными ионами.
Каждый из k процессов характеризуется своим сечением σka взаимодействия частиц плазмы с нейтральными атомами диагностического пучка. Ослабление пучка атомов с начальной плотностью na можно записать так:
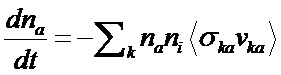
(усреднение производится по функции распределения соответствующих частиц),
где
vka - относительная скорость сталкивающихся частиц;
σka - сечение процесса;
nk - плотность соответствующего типа частиц.
Плотность тока пучка, прошедшего через плазму, при учете трех основных процессов рассчитывается по формуле:
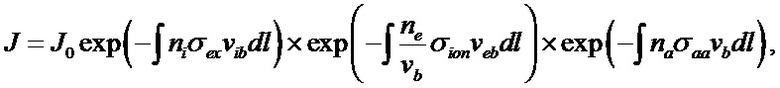
где
σех - сечение перезарядки,
σion - сечение ионизации электронным ударом,
σаа - сечение обдирки на атомах.
Таким образом, для определения плотности ионов многокомпонентной плазмы необходимо знать функции распределения ионов и электронов плазмы и сечения процессов, вносящих вклад в ослабление диагностического пучка. Это приводит к существенному понижению точности измерения ni. В связи с этим, данный метод находит применение лишь когда плазма находится в области сильного магнитного поля и поэтому вывод ионов из плазмы в систему регистрации невозможен из-за «запирания» ионов магнитным полем в плазменном объеме.
Прототипом заявляемого способа является способ по [Strokin N.A., Kazantsev A.V., Bardakov V.M., Thang The Nguyen, and Kuzmina A.S. Jumping the anode layer in the zone of the E×B discharge // Physics of Plasmas, 2019. - V. 26, No. 7. - 073501].
Способ по прототипу реализуется следующим образом:
1) измеряют вольт-амперную характеристику - кривую задержки
Ii = f(Uан)
для ионов, покидающих плазму, с помощью Энергоанализатора с Задерживающим Потенциалом (ЭЗП),
где
Ii - ток ионов, изменяющийся от максимального значения - полный ток при Uан = 0, до 0 при Uан = еWмакс;
Wмакс - максимальная энергия анализируемых ионов;
Uан - напряжение на анализирующей сетке ЭЗП;
2) дифференцируют зависимость Ii = f(Uан) - получают зависимость 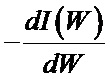 , характеризующую распределение ионов по энергии - энергетический спектр ионов;
, характеризующую распределение ионов по энергии - энергетический спектр ионов;
3) рассчитывают функцию распределения ионов по энергии:
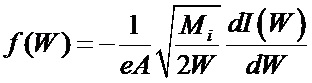 ;
;
4) рассчитывают плотность ионов как интеграл от функции распределения в диапазоне энергий от 0 до Wмакс:
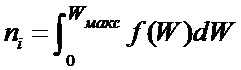 .
.
Признаками способа по прототипу, совпадающими с существенными признаками заявляемого способа, являются:
1) измеряют вольт-амперную характеристику - кривую задержки
Ii = f(Uан)
для ионов, покидающих плазму, с помощью энергоанализатора с задерживающим потенциалом,
где
Ii - ток ионов, изменяющийся от максимального значения - полный ток при Uан = 0, до 0 при Uан = еWмакс;
Wмакс - максимальная энергия анализируемых ионов
Uан - напряжение на анализирующей сетке ЭЗП;
2) дифференцируют зависимость Ii = f(Uан) - получают зависимость 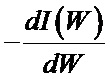 , характеризующую распределение ионов по энергии - энергетический спектр ионов;
, характеризующую распределение ионов по энергии - энергетический спектр ионов;
3) рассчитывают функцию распределения ионов по энергии:
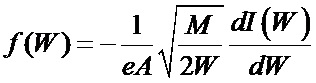 ,
,
4) численными методами рассчитывают плотность ионов как интеграл от функции распределения в диапазоне энергий от 0 до Wмакс:
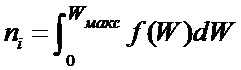 .
.
Недостатком способа по прототипу является:
1) при работе с многокомпонентной плазмой существует неопределенность в выборе массы иона М в формуле 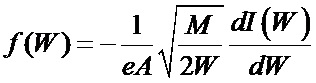 , что приводит к ошибкам в определении плотности ионов.
, что приводит к ошибкам в определении плотности ионов.
При создании способа поставлена задача разработать способ, в котором остаются все положительные качества способа по прототипу и обеспечена возможность определения плотности ионов многокомпонентной плазмы с более высокой точностью.
Технический результат достигается тем, что в способе измерения плотности ионов многокомпонентной плазмы, включающем измерение кривой задержки Ii = f(Uан) ЭЗП для ионов, покидающих плазму, получение зависимости 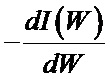 , характеризующей энергетический спектр ионов, расчет функции распределения ионов по энергии
, характеризующей энергетический спектр ионов, расчет функции распределения ионов по энергии 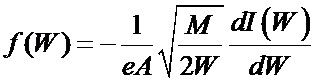 , расчет плотности ионов
, расчет плотности ионов 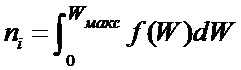 , согласно изобретению определяют эффективную массу ионов Meff с учетом парциальных вкладов ионов всех масс, содержащихся в исследуемой плазме, парциальные вклады ионов разных масс определяют по соотношениям наиболее сильных атомарных линий излучения соответствующих масс, расчет функции распределения ионов по энергии проводят по формуле
, согласно изобретению определяют эффективную массу ионов Meff с учетом парциальных вкладов ионов всех масс, содержащихся в исследуемой плазме, парциальные вклады ионов разных масс определяют по соотношениям наиболее сильных атомарных линий излучения соответствующих масс, расчет функции распределения ионов по энергии проводят по формуле 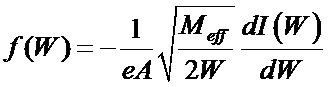 , плотность ионов рассчитывают как
, плотность ионов рассчитывают как 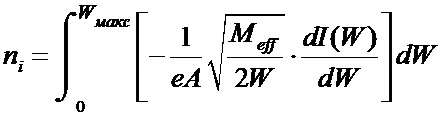 .
.
Преимуществом заявляемого способа определения плотности ионов, по сравнению с прототипом, является повышение точности определения плотности ионов, что позволяет рассматривать заявляемый способ в новом качестве - как способ определения плотности ионов многокомпонентной плазмы.
Заявляемый способ поясняется чертежами, приведенными на Фиг. 1-13.
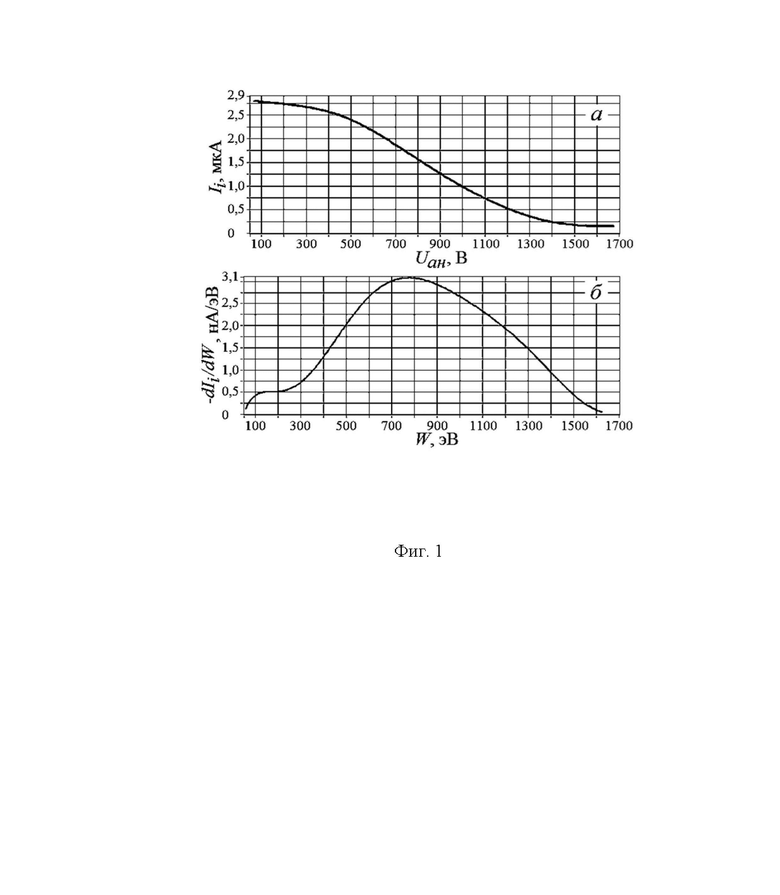
На Фиг. 1 приведен пример кривой задержки (а), и энергетический спектр 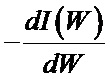 (б), которые получены при разрядном напряжении на аноде УАС UA = 1700 В, радиальной компоненте магнитного поля на аноде УАС BrA = 970 Гс, рабочем давлении Р = 1,5⋅10-4 торр; рабочая среда - смесь газов неона (Ne), аргона (Ar) и криптона (Kr) со скоростями напуска qNe = qAr = qKr = 6 sccm.
(б), которые получены при разрядном напряжении на аноде УАС UA = 1700 В, радиальной компоненте магнитного поля на аноде УАС BrA = 970 Гс, рабочем давлении Р = 1,5⋅10-4 торр; рабочая среда - смесь газов неона (Ne), аргона (Ar) и криптона (Kr) со скоростями напуска qNe = qAr = qKr = 6 sccm.
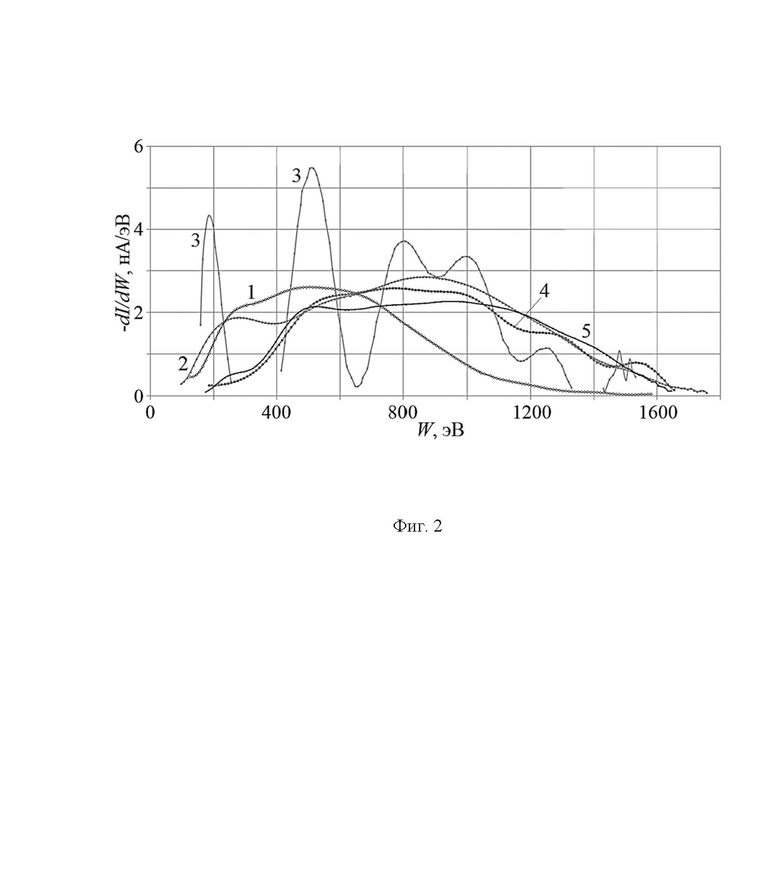
На Фиг. 2 показана эволюция распределения ионов по энергии при изменении величины индукции магнитного поля в разрядной камере УАС. Условия эксперимента: UA = 1700 В, Р = 1,5⋅10-4 торр; однокомпонентная рабочая среда: криптон, qKr = 13 sccm; спектр 1 получен при BrA = 340 Гс, 2 - 660 Гс, 3 - 820 Гс, 4 - 910 Гс, 5 - 980 Гс.
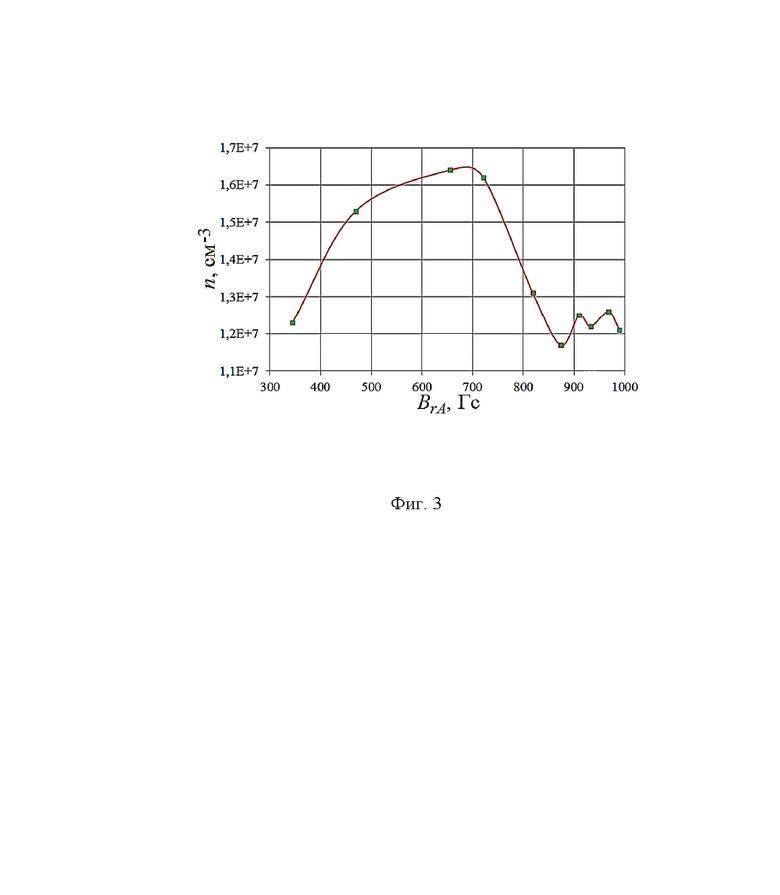
На Фиг. 3 приведен график n = f(BrA) зависимости плотности ионов от индукции магнитного поля, который получен из спектров, показанных на Фиг. 2. Условия эксперимента: UA = 1700 В, Р = 1,5⋅10-4 торр; однокомпонентная рабочая среда: криптон, qKr = 13 sccm; спектр 1 получен при BrA = 340 Гс, 2 - 660 Гс, 3 - 820 Гс, 4 - 910 Гс, 5 - 980 Гс.
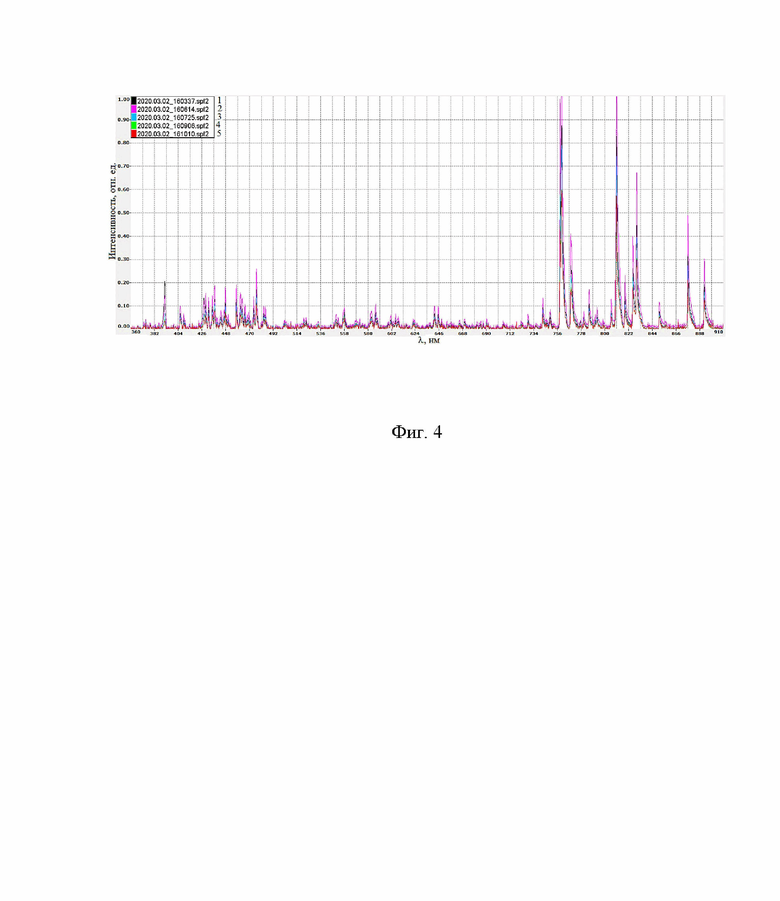
На Фиг. 4 показаны спектры излучения плазмы, которые соответствуют распределениям ионов по энергии, приведенным на Фиг. 2; по оси х - длина волны в нм, по оси y - интенсивность I линий в относительных единицах, нормированная на 1.
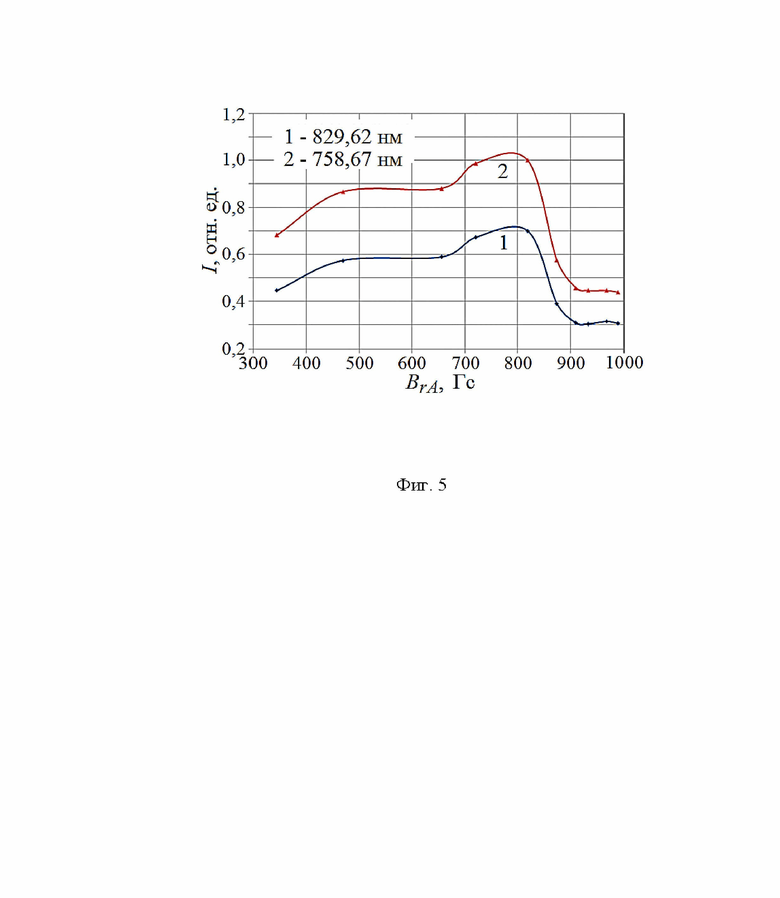
На Фиг. 5 приведены зависимости интенсивности I = f(BrA) сильных атомарных линий криптона: кривая 1 длина волны 829,62 нм, кривая 2 - 758,67 нм; данные линии есть (излучаются плазмой) при все магнитных полях, которые устанавливались в эксперименте.
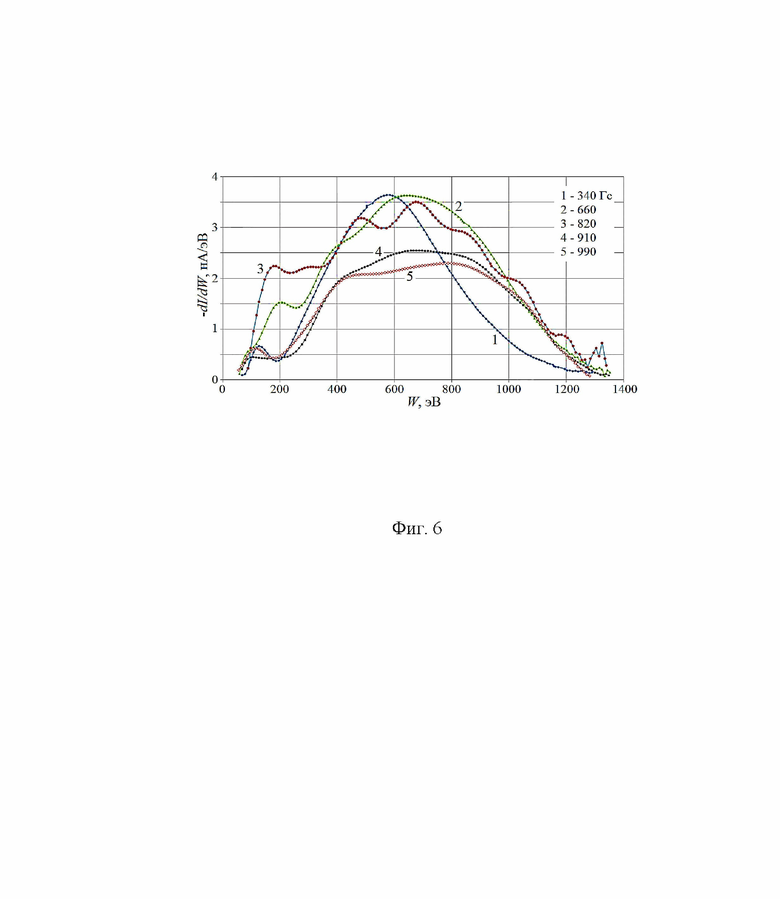
На Фиг. 6 даны спектры ионов по энергии в случае двухкомпонентной рабочей среды: аргон плюс криптон; BrA = 340÷ 990 Гс; UA = 1300 В; Р = 1,8⋅10-4 торр; qAr = qKr = 5 sccm.
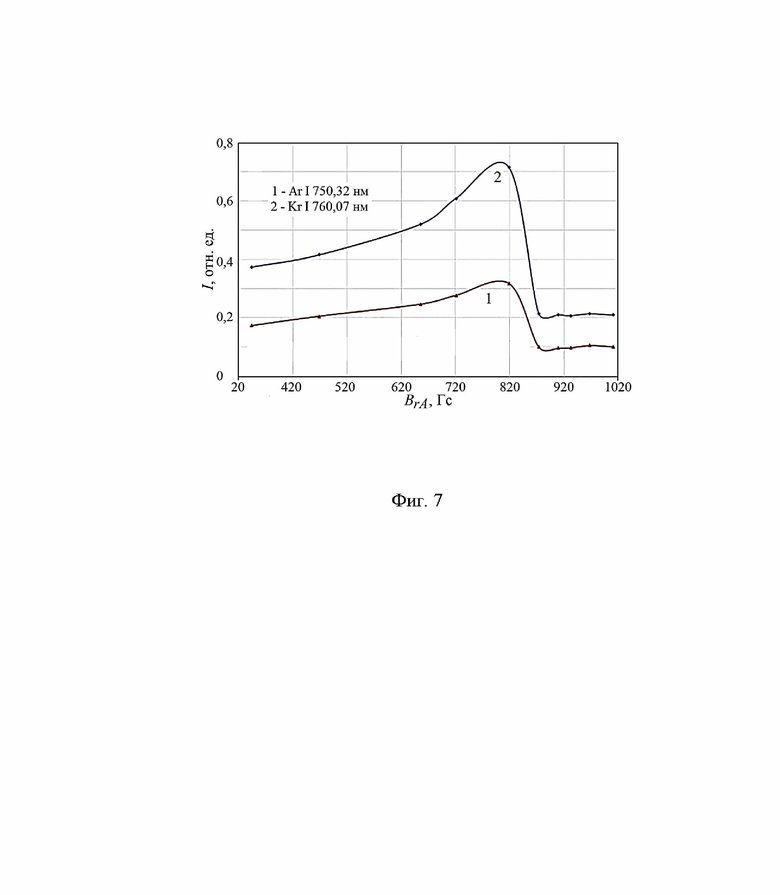
На Фиг. 7 приведены графики изменения интенсивности атомарных линий аргона Ar I 750,32 нм (кривая 1) и криптона Kr I 760,07 нм (кривая 2). Условия эксперимента: рабочая среда: аргон плюс криптон; BrA = 340 ÷ 990 Гс; UA = 1300 В; Р = 1,8⋅10-4 торр; qAr = qKr = 5 sccm.
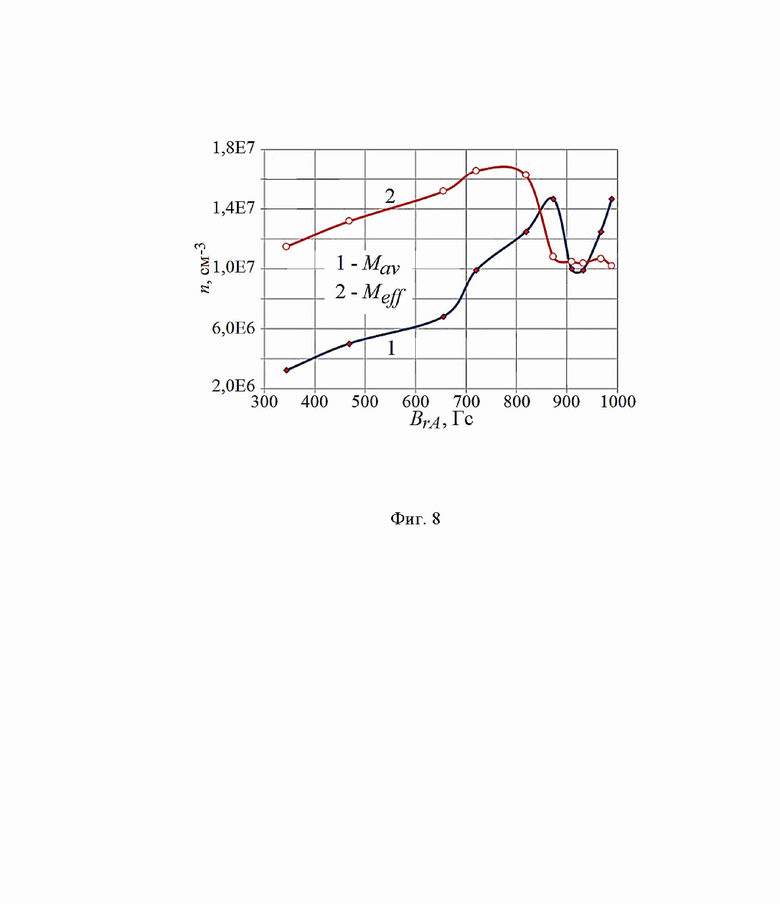
На Фиг. 8 приведены графики n = f(BrA): кривая 1 - когда расчет плотности проводился по средней массе ионов M = Мav = (МAr + MKr)/2; кривая 2 - M = Мeff. Условия эксперимента: рабочая среда: аргон плюс криптон; BrA = 340 ÷ 990 Гс; UA = 1300 В; Р = 1,8⋅10-4 торр; qAr = qKr = 5 sccm.
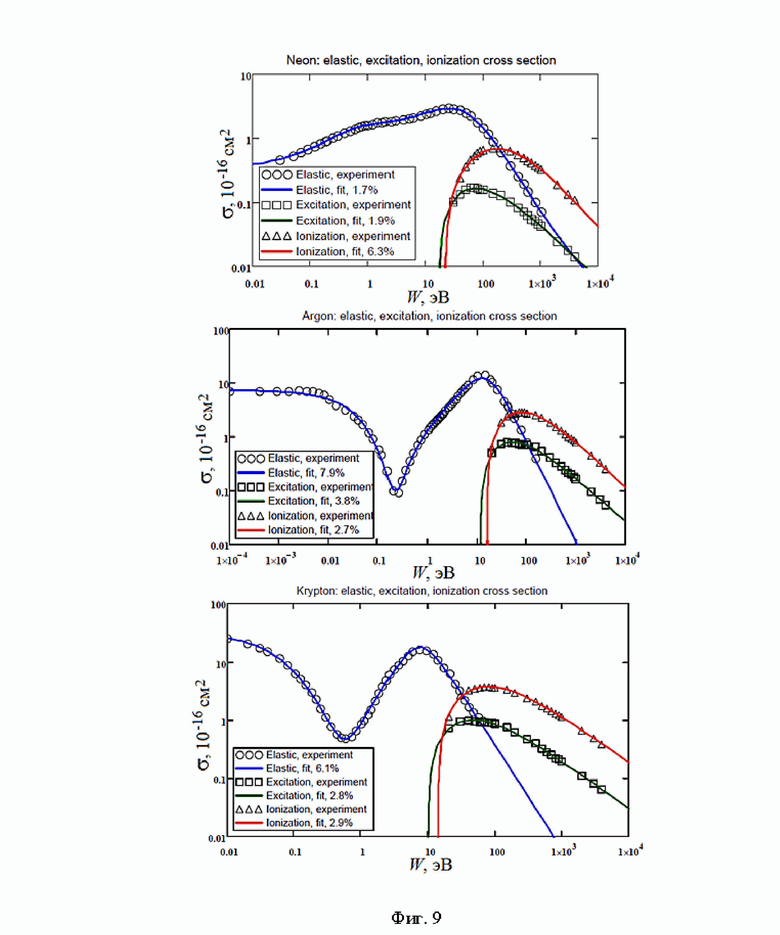
На Фиг. 9 приведены результаты аналитической аппроксимация сечений столкновений электронов с атомами инертных газов, которые адаптированы из статьи [Успехи прикладной физики, 2021. - Т. 9, №4. - С. 298-309; рис. 2-4].
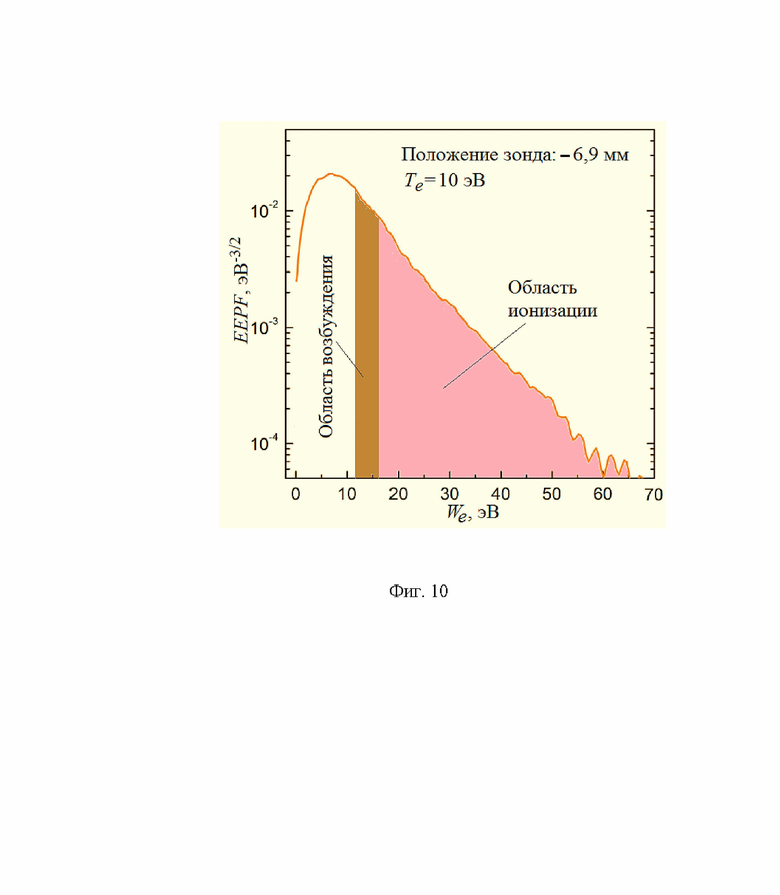
На Фиг. 10 приведена измеренная функция распределения электронов по энергии (вероятность) в камере плазменного ускорителя с протяженной зоной ускорения, где горит несамостоятельный разряд в скрещенных электрическом и магнитном полях [адаптирован рис. 4 из работы Tichy M., Petin A., Kudrna P., Horky M., and Mazouffre S. Electron energy distribution function in a low-power Hall thruster discharge and near-field plume // Physics of Plasmas, 2018. - V. 25. - 061205].
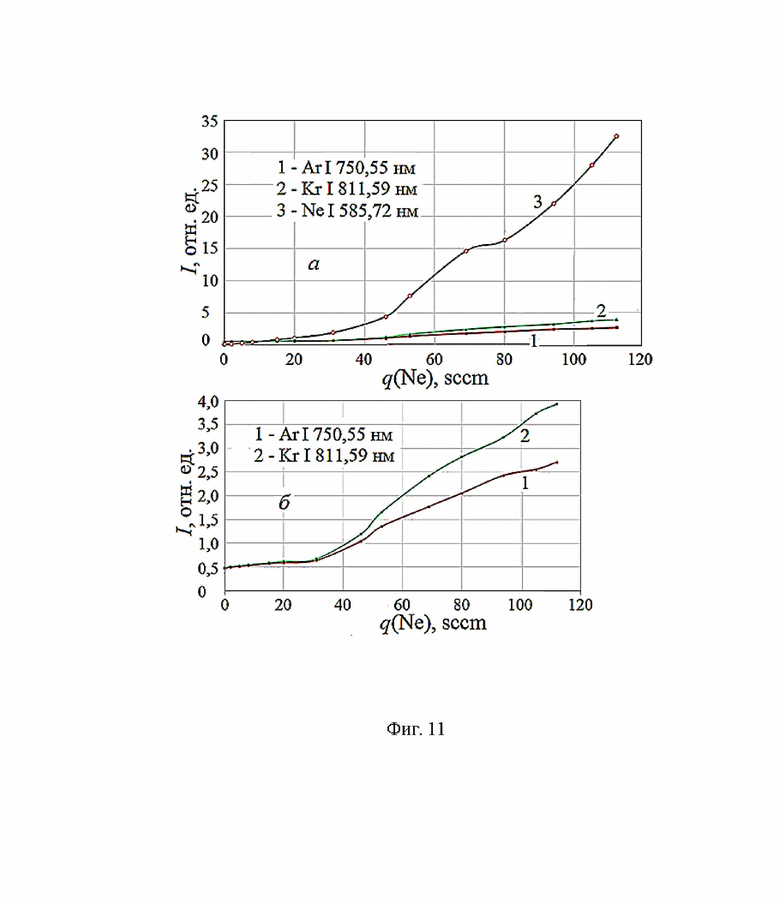
На Фиг. 11 иллюстрируется изменение интенсивностей линий трех возбужденных атомов: (а) - криптона Kr I 811,59 нм (кривая 1), аргона Ar I 750,55 нм (2) и неона Ne I 585,72 нм (3); (б) - аргона Ar I 750,55 нм (кривая 1) и криптона Kr I 811,59 нм (2). Условия эксперимента: qAr = qKr = 2 sccm; UA = 1100 В; BrA = 470 Гс.
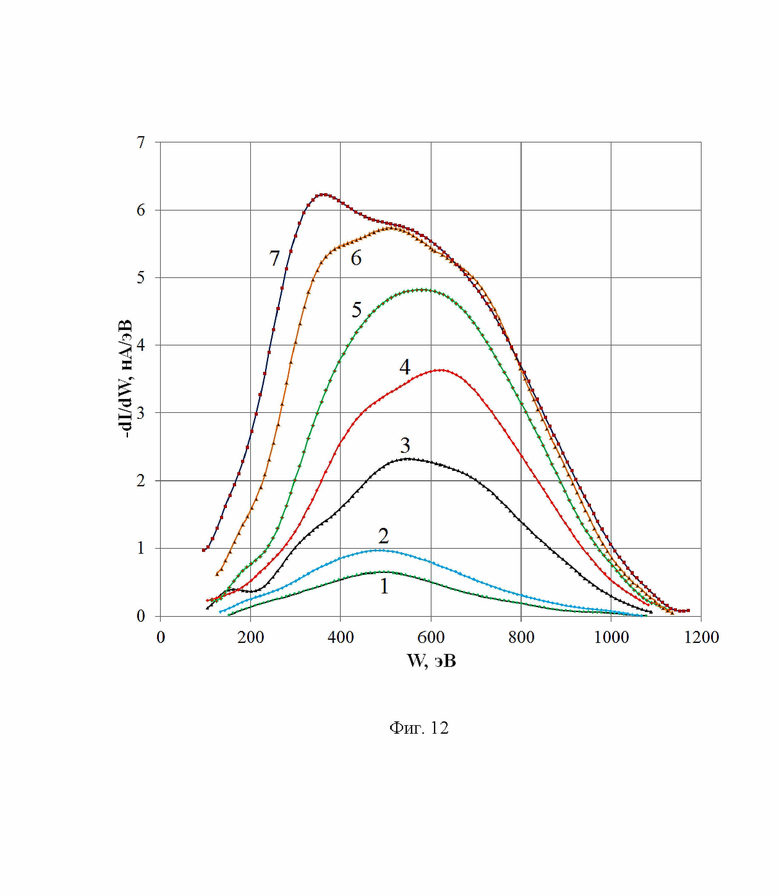
На Фиг. 12 демонстрируется эволюция энергетических спектров ионов при росте скорости напуска неона: кривая 1 qNe = 0 sccm, 2 - 20, 3 - 46, 4 - 58, 5 - 69, 6 - 94, 7 - 112. Условия эксперимента: qAr = qKr = 2 sccm; UA = 1100 В; BrA = 470 Гс.
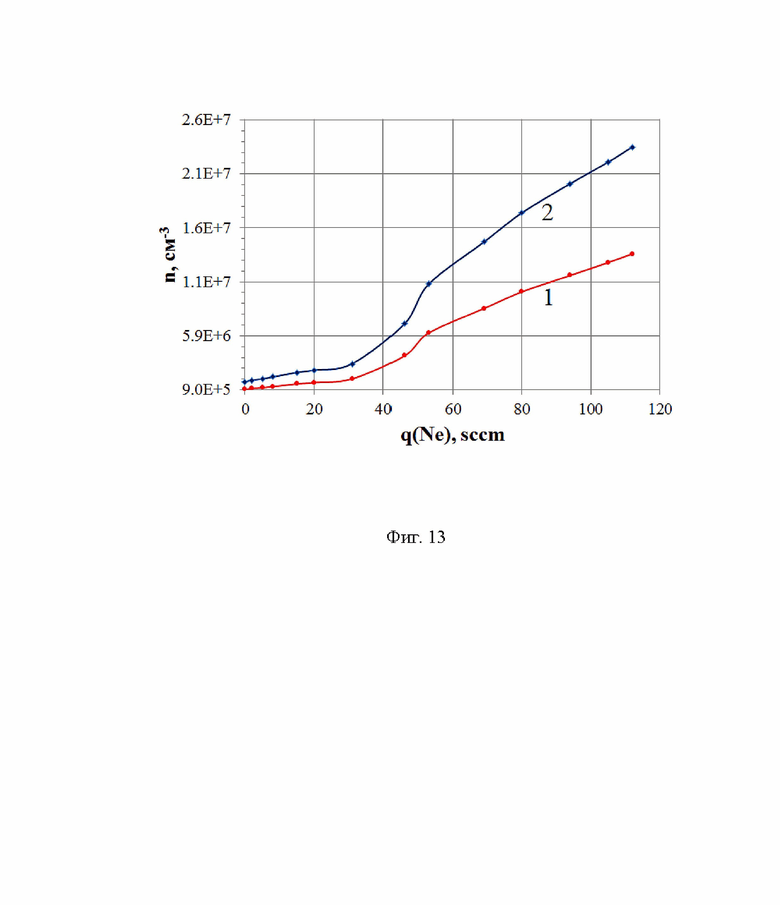
На Фиг. 13 приведены зависимости плотности ионов, рассчитанные по энергетическим спектрам, приведенным на Фиг. 12, от скорости напуска неона: кривая 1 - M = MNe; кривая 2 - M = Meff. Условия эксперимента: qAr = qKr = 2 sccm; UA = 1100 В; BrA = 470 Гс.
Опишем использование заявляемого способа на примере измерения плотности одно-, двух- и трехкомпонентного потока ионов инертных газов (неон, аргон, криптон) из плазменного Ускорителя с Анодным Слоем (УАС), в котором горит самостоятельный стационарный разряд в скрещенных электрическом и магнитном полях.
Энергоанализатор с задерживающим потенциалом устанавливается вблизи кольцевого отверстия в катоде УАС - на выходе УАС. Изменяя напряжение Uан на анализирующей сетке УАС и измеряя суммарный по всем типам ионов ток, приходящий на коллектор УАС, получают кривую задержки Ii = f(Uан). На Фиг. 1а приведен пример кривой задержки, на Фиг. 1б - энергетический спектр 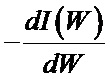 , когда разрядное напряжение на аноде УАС UA = 1700 В, радиальная (основная в разрядном промежутке УАС) компонента магнитного поля на аноде УАС BrA = 970 Гс, рабочее давление Р = 1,5⋅10-4 торр, рабочая среда - смесь газов неона (Ne), аргона (Ar) и криптона (Kr) со скоростями напуска qNe = qAr = qKr = 6 стандартных кубических сантиметров в минуту (sccm).
, когда разрядное напряжение на аноде УАС UA = 1700 В, радиальная (основная в разрядном промежутке УАС) компонента магнитного поля на аноде УАС BrA = 970 Гс, рабочее давление Р = 1,5⋅10-4 торр, рабочая среда - смесь газов неона (Ne), аргона (Ar) и криптона (Kr) со скоростями напуска qNe = qAr = qKr = 6 стандартных кубических сантиметров в минуту (sccm).
Целью научных исследований, обычно, является получение сведений о поведении заданного плазменного параметра, в нашем случае - плотности ионов при изменении внешних воздействий в максимально широком диапазоне значений. На Фиг. 2 приведен пример эволюции распределения ионов по энергии при изменении величины индукции магнитного поля в разрядной камере УАС. Условия эксперимента: UA = 1700 В, Р = 1,5⋅10-4 торр, рабочая среда - криптон (однокомпонентная), qKr = 13 sccm; спектр 1 получен при BrA = 340 Гс, 2 - 660 Гс, 3 - 820 Гс, 4 - 910 Гс, 5 - 980 Гс. Распределения ионов по энергии при росте BrA сдвигаются как целое в сторону высоких энергий, проходя через неустойчивый (много-пучковый спектр - кривая 3) режим разряда.
Полученные спектры ионов по энергии позволяют одним из численных методов при известной площади коллектора и диапазоне энергий, предварительно (обычно) выполнив аппроксимацию кривой задержки (сплайнами или полиноминальную), рассчитать плотность ионов по формуле: 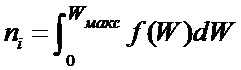 . На Фиг. 3 приведен график n = f(BrA) зависимости плотности ионов от индукции магнитного поля, который получен из спектров, показанных на Фиг. 2.
. На Фиг. 3 приведен график n = f(BrA) зависимости плотности ионов от индукции магнитного поля, который получен из спектров, показанных на Фиг. 2.
Одновременно с измерением энергетического спектра ионов осуществляется регистрация спектров излучения плазмы, которые, для иллюстрации, приведены на Фиг. 4 и соответствуют распределениям ионов по энергии, которые приведены на Фиг. 2; по оси х - длина волны в нм, по оси y - интенсивность I линии в относительных единицах, нормированная на 1. Выбрав сильные атомарные линии криптона, например, с длиной волны 758,67 и 829,62 нм, которые есть при все магнитных полях, можно построить зависимости I = f(BrA), которые приведены на Фиг. 5.
Ход зависимостей n = f(BrA) и I = f(BrA) можно сравнить между собой. Видно, что плотность ионов и интенсивность излучения возбужденных атомов коррелируют между собой.
Приведем пример двухкомпонентной плазмообразующей среды: аргон плюс криптон; qAr = qKr = 5 sccm; UA = 1300 В; Р = 1,8⋅10-4 торр; магнитное поле - изменяется в диапазоне 340 ÷ 990 Гс. На Фиг. 6 даны спектры ионов по энергии, на Фиг. 7 - соответствующие им графики изменения интенсивности атомарных линий аргона Ar I 750,32 нм (кривая 1) и криптона Kr I 760,07 нм (2).
Дальше необходимо, рассчитав функцию распределения 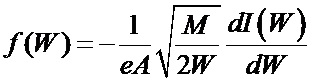 , проинтегрировав f(W), посмотреть ход плотности при изменении магнитного поля. Но возникает вопрос: какую массу подставлять в формулу для f(W). И число атомов Ar и Kr в рабочем объеме (при одинаковой скорости напуска) разное, и потенциалы ионизации разные: ϕAr = 15,68 эВ; ϕKr = 14 эВ. На Фиг. 8 (кривая 1) приведен график n = f(BrA) при средней массе Мav = (МAr + MKr)/2. С учетом вышесказанного, есть недоверие к такой величине массы и, следовательно, зависимости n = f(BrA).
, проинтегрировав f(W), посмотреть ход плотности при изменении магнитного поля. Но возникает вопрос: какую массу подставлять в формулу для f(W). И число атомов Ar и Kr в рабочем объеме (при одинаковой скорости напуска) разное, и потенциалы ионизации разные: ϕAr = 15,68 эВ; ϕKr = 14 эВ. На Фиг. 8 (кривая 1) приведен график n = f(BrA) при средней массе Мav = (МAr + MKr)/2. С учетом вышесказанного, есть недоверие к такой величине массы и, следовательно, зависимости n = f(BrA).
Анализируя атомарные спектры излучения, можно определить соотношение интенсивностей линий излучения различных атомов. Так для интенсивности линий излучения, приведенных на Фиг. 7, значения соотношений интенсивностей даны в таблице 1.
Средняя величина [I(KrI)/I(ArI)]ср ≈ 2,13; максимальное отклонение от средней величины составляет около 6%.
Можно предложить ввести эффективную массу Meff, в которую массы аргона и криптона будут входить в соотношениях, равных отношениями интенсивностей излучения линий аргона и криптона при тех же экспериментальных условиях. Такое предложение основывается на ожидаемом свойстве: число ионов каждой компоненты газовой смеси прямо пропорционально числу возбужденных атомов того же типа. Базой для такого предложения является одинаковая функциональная зависимость сечений возбуждения σex и ионизации σion [Голятина Р.И., Майоров С.А. Аналитическая аппроксимация сечений столкновений электронов с атомами инертных газов // Успехи прикладной физики, 2021. - Т. 9, №4. - С. 298-309; рис. 2-4], которые приведены на Фиг. 9.
Кроме того, распределение электронов плазмы по энергии в разряде в скрещенных электрическом и магнитном полях имеет одинаковую функциональную зависимость в диапазоне энергий электронов, осуществляющих столкновительное возбуждение нейтралов, и рядом - когда происходит ионизация атомов электронным ударом; сохраняется постоянное соотношение между возбужденными и ионизованными атомами при измерении внешних параметров разряда. Это можно проиллюстрировать Фиг. 10, на которой приведена измеренная функция распределения электронов по энергии (вероятность) в камере плазменного ускорителя с протяженной зоной ускорения, где горит несамостоятельный (есть дополнительный внешний источник электронов) разряд в скрещенных электрическом и магнитном полях [адаптированный рис. 4 из работы Tichy M., Petin A., Kudrna P., Horky M., and Mazouffre S. Electron energy distribution function in a low-power Hall thruster discharge and near-field plume // Physics of Plasmas, 2018. - V. 25. - 061205].
Учитывая сказанное, Фиг. 8, где уже приведен график n = f(BrA), построенный для случая M = Mav = 61,9 а.е.м. (кривая 1), дополнена кривой 2, для которой M = Meff = 70,1 а.е.м..
Сравнивая данные, показанные на Фиг. 7 и Фиг. 8, можно сделать вывод о том, что функциональные зависимости плотности ионов и интенсивности излучения одинаковые в случае использования M = Meff .
Приведем пример определения зависимости плотности ионов от давления трехкомпонентного (Ne, Ar, Kr) плазмаобразующего газа, которое изменяется при росте скорости напуска одного из газов - неона: n = f(qNe); при этом qAr = qKr = 2 sccm; UA = 1100 В; BrA = 470 Гс. Для расчета парциальных коэффициентов при каждом из значений qNe при определении Meff использовались сильные линии излучения Ne I 585,72 нм; Ar I 750,55 нм; Kr I 811,59 нм. Например, при qNe = 53 sccm эффективная масса рассчитывалась так: Meff = I(Ne)⋅MNe + I(Ar)⋅MAr + I(Kr)⋅MKr = 14,45⋅20,179 + 13,07⋅39,498 + 5,11⋅83,8 = 32,63 а.е.м., где I(Ne), I(Ar) и I(Kr) - относительные интенсивности линий неона, аргона и криптона. Изменение интенсивностей линий трех возбужденных атомов иллюстрируется Фиг. 11 (а - три газа; б - без неона - аргон и криптон).
На Фиг. 12 показана эволюция энергетических спектров ионов при росте скорости напуска неона: кривая 1 qNe = 0 sccm, 2 - 20, 3 - 46, 4 - 58, 5 - 69, 6 - 94, 7 - 112. Площадь под спектрами монотонно растет с опережающим ростом числа сравнительно низкоэнергетичных (W ≤ 400 эВ) ионов.
По спектрам Фиг. 12 вычислены и построены зависимости плотности ионов от скорости напуска неона, которые приведены на Фиг. 13: кривая 1 - M = MNe; кривая 2 - M = Meff. Зависимости 1 и 2 расходятся: разность [n(MNe) - n(MNe)] с ростом qNe - уменьшением парциального вклада аргона и криптона в давление смеси нейтральных газов, растет. Это неочевидный эффект, требующий изучения, в том числе, и с учетом возможного влияния метастабильного возбужденного состояния неона, потенциал возбуждения которого ϕex.m ≈ 16,7 эВ больше потенциалов ионизации ϕAr, ϕKr.
Как следует из приведенного обоснования, есть прямой способ определения плотности ионов - как интеграла от функции распределения ионов по энергии. Непосредственное измерение плотности ионов в низкотемпературной плазме со степенью ионизации меньшей 100 %, без магнитного поля и с магнитным полем, величина которого недостаточна для замагничивания ионов (ларморовский радиус ионов много больше характерных размеров области разряда), возможно с помощью, например, энергоанализатора с задерживающим потенциалом. Однако ЭЗП дает суммарный спектр ионов в случае многокомпонентной плазмы, интегрируя который нельзя с достаточной точностью вычислить суммарную плотность ионов из-за невозможности учесть парциальные вклады ионов всех плазмообразующих газов. Как было выяснено в процессе работы над заявляемым изобретением, зависимости интенсивностей сильных линий излучения возбужденных атомов и энергетические спектры ионов подобным образом зависят от величины индукции магнитного поля, рабочих давления и разрядного напряжения. Причем отношение интенсивностей I сильных линий возбужденных атомов остается с точностью ~ 10% постоянным во всем диапазоне изменения магнитной индукции в используемом УАС (на аноде BrA = 340 ÷ 1100 Гс; на катоде - в области генерации эмиссионных электронов изменяется, соответственно, от 1360 до 4000 Гс). Оценивать парциальный вклад ионов в формирование кривой задержки ЭЗП можно по отношению интенсивностей сильных линий возбужденных атомов. В таком случае при вычислении плотности ионов по функции распределения ионов по энергии нужно вводить «эффективную массу» ионов в соответствии с их парциальным вкладом в суммарную интенсивность выбранных линий, например, в трехкомпонентной плазме: Meff = I(Ne)⋅MNe + I(Ar)⋅MAr + I(Kr)⋅MKr, где I(Ne), I(Ar) и I(Kr) - относительные интенсивности линий неона, аргона и криптона.
Затруднений с получением спектров излучения нет. Техника спектроскопии излучения плазмы развита хорошо: выпускается ряд спектрометров, например, с оптоволоконными каналами регистрации, измерения которыми можно проводить одновременно со снятием энергетических спектров ионов и выделять в спектрах излучения наиболее сильные линии возбужденных атомов.
Таким образом, заявляется способ определения плотности ионов в многокомпонентной плазме в рамках прямого измерения распределений ионов по энергии и определения плотности в процессе численного интегрирования функции распределения, вводя в расчетную формулу эффективную массу ионов с учетом парциального вклада ионов всех масс, формирующий рабочий плазмаобразующий газ.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ анализа ионов по энергиям, массам и зарядам и устройство для его осуществления | 2019 |
|
RU2708637C1 |
| Способ формирования пучка ионов плазмооптического масс-сепаратора и устройство для его осуществления | 2017 |
|
RU2681524C1 |
| СПОСОБ ОБРАБОТКИ ПОДЛОЖКИ | 2006 |
|
RU2410341C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭЛЕМЕНТНОГО СОСТАВА И ТОЛЩИНЫ ПОВЕРХНОСТНОЙ ПЛЕНКИ ТВЕРДОГО ТЕЛА ПРИ ВНЕШНЕМ ВОЗДЕЙСТВИИ НА ПОВЕРХНОСТЬ | 2012 |
|
RU2522667C2 |
| СПОСОБ АНАЛИЗА ЗАРЯЖЕННЫХ ЧАСТИЦ ПО МАССАМ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2431214C1 |
| СПОСОБ ПОЛУЧЕНИЯ ИЗНОСОСТОЙКИХ СВЕРХТВЕРДЫХ ПОКРЫТИЙ | 2007 |
|
RU2360032C1 |
| СПОСОБ ПАНОРАМНОЙ ПЛАЗМЕННОЙ МАСС-СЕПАРАЦИИ И УСТРОЙСТВО ПАНОРАМНОЙ ПЛАЗМЕННОЙ МАСС-СЕПАРАЦИИ (ВАРИАНТЫ) | 2011 |
|
RU2469776C1 |
| Способ модифицирования поверхности высокомодульного углеродного волокнистого материала | 2018 |
|
RU2689584C1 |
| Способ определения характеристик ионизованной среды | 1991 |
|
SU1805350A1 |
| Масс-спектрометрический способ анализа твердых тел | 1982 |
|
SU1105962A1 |
Изобретение относится к способам и устройствам для анализа ионов по энергиям, массам, зарядам с использованием электрических и магнитных полей и расчетам по результатам анализа плотности ионов плазмы и может быть использовано для определения характеристик, например потоков плазмы рабочего вещества технологических ускорителей плазмы и плазменных двигателей. Технический результат - повышение точности определения плотности ионов многокомпонентной плазмы. В способе измерения плотности ионов многокомпонентной плазмы измеряют оптический спектр излучения многокомпонентной плазмы для выделения в спектре наиболее сильных атомарных линий излучения атомов всех масс из исследуемого потока, определения парциальных вкладов ионов разных масс и эффективной массы ионов, на поток ионов, поступающих в энергоанализатор с задерживающим потенциалом, воздействуют электрическим полем, тормозящим ионы, для измерения кривой задержки I=f(Uaн), определения функции распределения ионов многокомпонентного потока по энергии и плотности ионов многокомпонентного потока по расчетной формуле. 13 ил.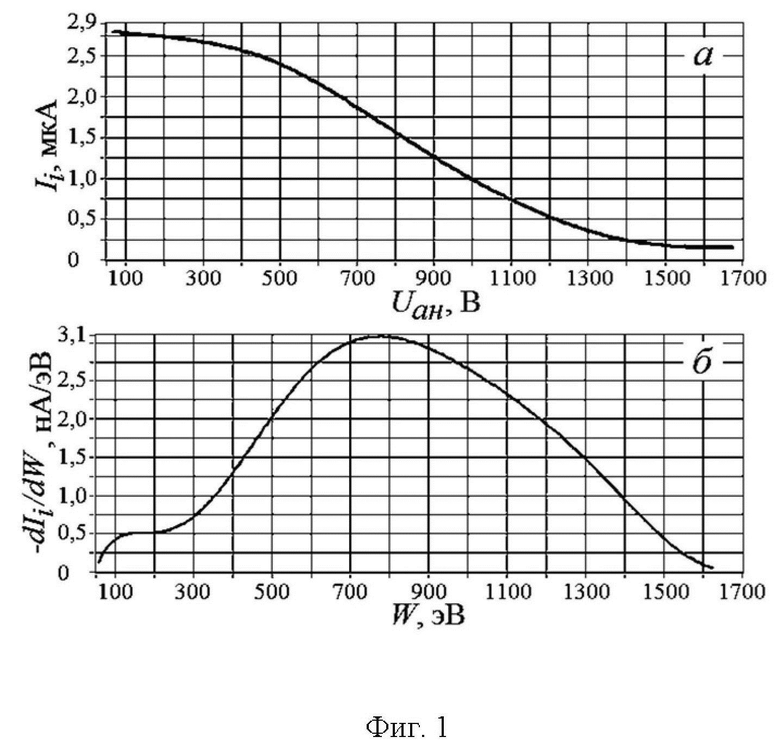
Способ измерения плотности ионов многокомпонентной плазмы, заключающийся в том, что на поток ионов, поступающих в энергоанализатор с задерживающим потенциалом, воздействуют электрическим полем, тормозящим ионы, для измерения кривой задержки I=ƒ(Uaн), определения функции распределения ионов по энергии 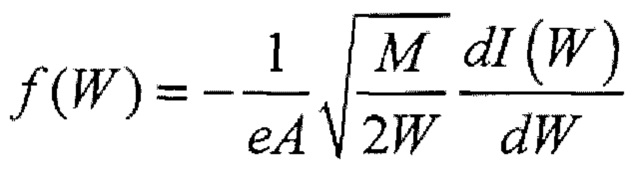 и плотности ионов
и плотности ионов 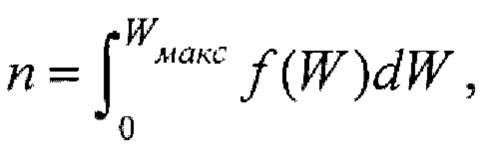 отличающийся тем, что измеряют оптический спектр излучения многокомпонентной плазмы для выделения в спектре наиболее сильных атомарных линий излучения атомов всех масс из исследуемого потока, определения парциальных вкладов ионов разных масс и эффективной массы ионов Мeƒƒ, на поток ионов, поступающих в энергоанализатор с задерживающим потенциалом, воздействуют электрическим полем, тормозящим ионы, для измерения кривой задержки I=ƒ(Uaн), определения функции распределения ионов многокомпонентного потока по энергии
отличающийся тем, что измеряют оптический спектр излучения многокомпонентной плазмы для выделения в спектре наиболее сильных атомарных линий излучения атомов всех масс из исследуемого потока, определения парциальных вкладов ионов разных масс и эффективной массы ионов Мeƒƒ, на поток ионов, поступающих в энергоанализатор с задерживающим потенциалом, воздействуют электрическим полем, тормозящим ионы, для измерения кривой задержки I=ƒ(Uaн), определения функции распределения ионов многокомпонентного потока по энергии 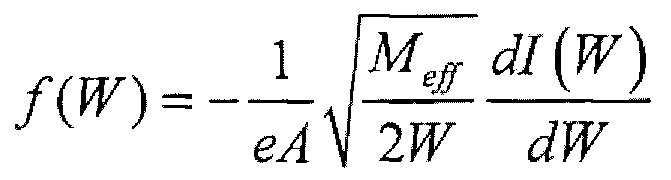 и плотности ионов многокомпонентного потока
и плотности ионов многокомпонентного потока 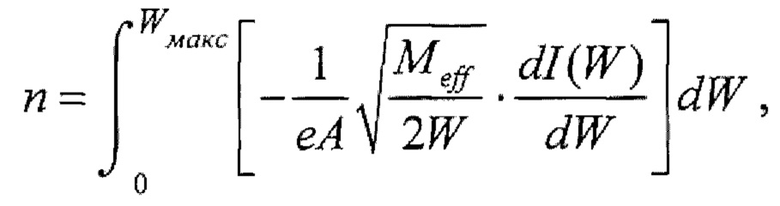
где I - ток ионов, А;
Uан - тормозящее ионы напряжение на анализирующей сетке энергоанализатора с задерживающим потенциалом, В;
W - энергия ионов, Дж;
Wмакс - максимальная энергия ионов из исследуемого диапазона энергий, Дж;
ƒ(W) - функция распределения ионов по энергии, относительных единиц;
е - заряд электрона, Кл;
М - масса иона, кг;
Meƒƒ - эффективная масса иона, кг;
n - плотность ионов, м-3;
А - площадь коллектора энергоанализатора с задерживающим потенциалом, м2.
| STROKIN N.A | |||
| Jumping the anode layer in the zone of the E'B discharge, Physics of Plasmas, 2019, v | |||
| Прибор для получения стереоскопических впечатлений от двух изображений различного масштаба | 1917 |
|
SU26A1 |
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| US 11735397 В2, 22.08.2023 | |||
| US 2019242838 A1, 08.08.2019 | |||
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ КОНЦЕНТРАЦИИ ЗАРЯЖЕННЫХ ЧАСТИЦ | 2009 |
|
RU2515207C2 |
| US 2008000585 A1, 03.01.2008 | |||
| НИКИШИН А.В | |||
| Многохордовая пучковая диагностика плазмы на установке ГОЛ-NB, Физика плазмы, 2022, т | |||
| Приспособление для автоматической односторонней разгрузки железнодорожных платформ | 1921 |
|
SU48A1 |
Авторы
Даты
2024-04-16—Публикация
2023-10-11—Подача