Заявленное изобретение относится к средствам для работы с документами. В повседневной жизни часто возникает необходимость оцифровки документов. Ранее эта задача решалась при помощи сканеров и систем распознавания. С распространением мобильных телефонов изображения, полученные с камеры, стали более популярны, чем отсканированные изображения. Системы распознавания, запускаемые на таких изображениях, могут испытывать трудности. Например, образ документ (а значит, и текст на документе) может быть проективно искажен, так что нельзя рассчитывать на высокое качество распознавания систем, рассчитанных на сканеры. Поэтому перед распознаванием необходим дополнительный этап - получение ректифицированного изображения - изображение документа, как если бы он отсканирован на планшетном сканере. При получении ректифицированного изображения необходимо, чтобы содержимое документа не было никаким образом искажено (не было разрывов изображения, была сохранена горизонтальность строк и т.д.). Зачастую бывает так, что деловые документы хранятся в сложенном виде. Поэтому, когда возникает необходимость их оцифровать, нужно решить задачу ректификации документа, сложенного пополам.
Из уровня техники известны различные способы для получения ректифицированных изображений физически искаженных документов (см. документы Michael S Brown and W Brent Seales. Image restoration of arbitrarily warped documents. IEEE Transactions on pattern analysis and machine intelligence, 26(10):1295-1306, 2004 (1); Shaodi You, Yasuyuki Matsushita, Sudipta Sinha, Yusuke Bou, and Katsushi Ikeuchi. Multiview rectification of folded documents. IEEE transactions on pattern analysis and machine intelligence, 40(2):505-511, 2017 (2); Hao Feng, Yuechen Wang, Wengang Zhou, Jiajun Deng, and Houqiang Li. Doctr: Document image transformer for geometric unwarping and illumination correction. arXiv preprint arXiv: 2110.12942, 2021 (3); Gaofeng Meng, Chunhong Pan, Shiming Xiang, Jiangyong Duan, and Nanning Zheng. Metric rectification of curved document images. IEEE transactions on pattern analysis and machine intelligence, 34(4):707-722, 2011 (4)), однако они не предназначены для решения задачи развертки сложенных пополам документов по одному изображению, полученному с камеры мобильного телефона: в (1) предлагается использовать внешнее дополнительного оборудование, в работе (2) необходимо наличие нескольких изображений на входе, нейросетевой подход (3) не учитывает проективных искажений, возникающих при съемке камерой, в работе (4) накладывается существенное ограничение на модель документа - он должен быть представлен гладкой цилиндрической поверхностью с направляющими, параллельными текстовым строкам. Из источника информации (5) (см. Sagnik Das, Gaurav Mishra, Akshay Sudharshana, and Roy Shilkrot. The common fold: utilizing the four-fold to dewarp printed documents from a single image. In Proceedings of the 2017 ACM Symposium on Document Engineering, pages 125-128, 2017) известен способ для развертки документов, сложенных в несколько раз - это статья. Однако в (5), во-первых, не учитываются проективные искажения, возникающие при съемке камерой, а во-вторых, при детекции каждой части документа по отдельности и последующей склейке возникает разрыв контента на местах склейки.
Предложенный способ позволяет решать задачу развертки сложенных документов по одному изображению, полученному с камеры мобильного телефона и обладает следующими преимуществами:
- не требует дополнительного оборудования в отличие от (1).
- принимает на вход одно изображение в отличие от (2).
- учитывает проективные искажения в отличие от (3), (5).
- гарантирует отсутствие разрыва на сгибе в отличие от (5).
Помимо этого, важными деталями является то, что предложенный способ подходит для запуска на мобильном телефоне, а также устойчив к частичной окклюзии края документа - например, если его часть скрыта рукой.
Задачей заявленного изобретения является устранение недостатков известного уровня техники. Технический результат заключается в обеспечении способа получения ректифицированных изображений документов, сложенных пополам, который позволяет обеспечить повышение качества развертки сложенных документов по одному изображению, полученному с камеры мобильного телефона и при этом представленный способ не требует дополнительного оборудования, принимает на вход одно изображение, учитывает проективные искажения, обеспечивает отсутствие разрыва на сгибе, подходит для запуска на мобильном телефоне, а также устойчив к частичной окклюзии края документа - например, если его часть скрыта рукой.
Поставленная задача решается, а заявленный технический результат достигается посредством заявленного способа получения ректифицированных изображений документов, сложенных пополам.
Заявленный способ получения ректифицированных изображений документов, сложенных пополам заключается в поступлении на вход модели предъявления документа, причем верхняя половина изображения содержит большую часть верхней половины документа, а нижняя половина изображения содержит большую часть нижней половины документа, при этом высота больше ширины, при этом исходное изображение I делится пополам на верхнюю часть It и нижнюю часть Ib, строится грубое приближение половин документа двумя четырехугольниками, для этого к обеим половинам применяется алгоритм локализации четырехугольников, основанный на детекции границ и прямых, выходом которого является набор четырехугольников, отсортированных по их контурной оценке, таким образом получается множество четырехугольников Qt, расположенных на It и множество четырехугольников Qb, расположенных на Ib, при этом каждая пара четырехугольников используется для того, чтобы составить шестиугольник, который бы представлял внешние границы сложенного документа на изображении, к каждому сформированному и уточненному шестиугольнику применяется алгоритм коррекции, после этого шестиугольники сортируются по их контурной оценке и тот, у которого самая высокая контурная оценка является выходом из этапа локализации, последним этапом является отображение входного изображения, определяемого двумя проективными преобразованиями.
На фигурах представлены:
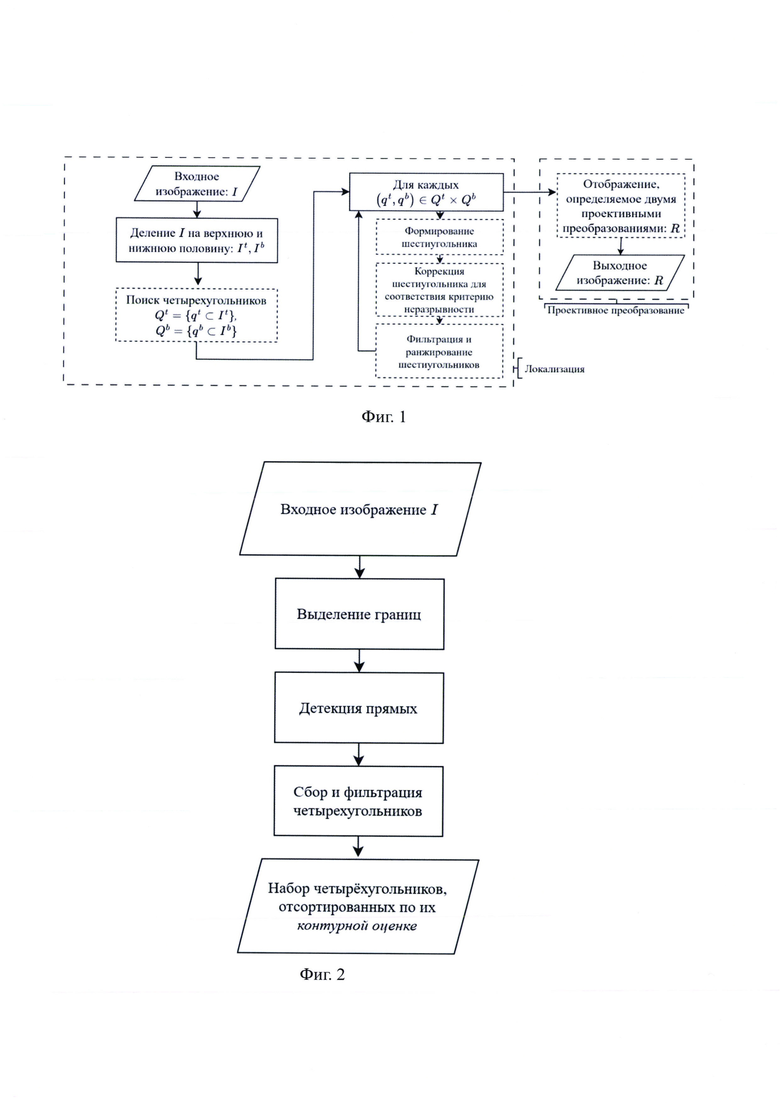
Фиг. 1: Блок-схема алгоритма, использованного в предлагаемом методе
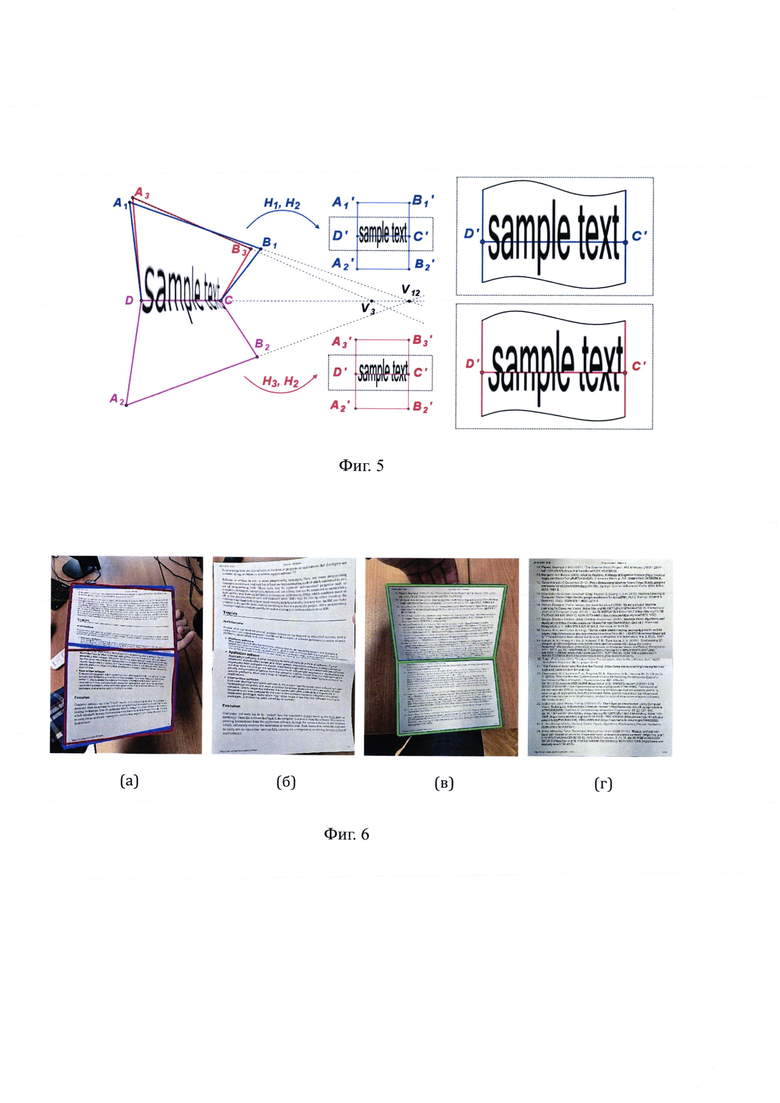
Фиг. 2: Блок-схема алгоритма детекции набора четырехугольников
Фиг. 3: (а) Горизонтальные (зеленые) и вертикальные (красные) границы на “общей” карте границ, (б) детектированные прямые (красные и зеленые) и синяя линия, разделяющая изображение пополам, (в) пара четырехугольников (верхний изображен голубым, нижний изображен желтым), истинная линия сгиба (зеленая) и линия сгиба, получена пересечением вертикальных отрезков (красная), (г) ломаная ABCD, аппроксимирующая излом границы на треке, выделенном штрихованным прямоугольником на (а), (д) локализованный шестиугольник, (е) границы, лежащие вдоль детектированного шестиугольника, (ж) ректифицированное изображение
Фиг. 4: Блок-схема алгоритма формирования шестиугольников
Фиг. 5: Примеры непрерывного (Н1, Н2) и разрывного (Н3, Н2) преобразования
Фиг. 6: Примеры неудовлетворительной и удовлетворительной ректификации: (а) входное изображение с детектированным шестиугольником (синий) и его корректировкой (красная), которая признана невалидной, (б) ректификация по красному шестиугольнику, (в) входное изображение с детектированным шестиугольником (синий) и его корректировкой (зеленая), которая признана валидной, (г) ректификация по зеленому шестиугольнику
Фиг. 7: Пример работы алгоритма: (а) Исходное изображение, (б) детектированные границы, (в) детектированные прямые, (г) найденные четырехугольники, (д) построенный и скорректированный шестиугольник, (е) ректифицированное изображение
Фиг. 8: Пример работы алгоритма: (а) Исходное изображение, (б) детектированные границы, (в) детектированные прямые, (г) найденные четырехугольники, (д) построенный и скорректированный шестиугольник, (е) ректифицированное изображение
Для использования предложенного метода необходимо:
- камера для получения входного изображения, например, камера смартфона;
- вычислительное устройство с любым современным процессором архитектуры ARM или x86, например, настольный компьютер или смартфон.
Пусть дано изображение, на котором находится документ формата А4, которое было получено при съемке камерой. Этот лист сложен пополам таким образом, что линия сгиба параллельна короткой стороне этого документа (далее - сложенный документ). Необходимо восстановить изображение этого документа, как если бы он был отсканирован на планшетном сканере. Далее это изображение будем называть ректифицированным, а саму задачу называть задачей ректификации.
В качестве метода решения задачи ректификации сложенного документа предлагается детектировать шестиугольник его внешней границы и проективно преобразовать каждую его половину по отдельности. Для реализации этого способа предлагается использовать следующий алгоритм.
Рассмотрим схему на фиг. 1. Предполагается, что модель предъявления документа такова, что верхняя половина изображения содержит большую часть верхней половины документа, а нижняя половина изображения содержит большую часть нижней половины документа, при этом высота больше ширины. Поэтому сначала исходное изображение I делится пополам на верхнюю часть It и нижнюю часть Ib, и строится грубое приближение половин документа двумя четырехугольниками. Для этого к обеим половинам применяется алгоритм локализации четырехугольников (раздел 1), основанный на детекции границ и прямых, выходом которого является набор четырехугольников, отсортированных по их контурной оценке. Таким образом получается множество четырехугольников Qt расположенных на It и множество четырехугольников Qb, расположенных на Ib.
Каждая пара четырехугольников используется для того, чтобы составить шестиугольник, который бы представлял внешние границы сложенного документа на изображении. Для того, чтобы составить такой шестиугольник, используются специальные уточняющие техники (раздел 2). К каждому сформированному и уточненному шестиугольнику применяется алгоритм коррекции (раздел 3) для того, чтобы он соответствовал критерию неразрывности. После этого шестиугольники сортируются по их контурной оценке и тот, у которого самая высокая контурная оценка является выходом из этапа локализации (раздел 4).
Последним этапом алгоритма является отображение входного изображения, определяемое двумя проективными преобразованиями. Полученное таким образом изображение является выходом предложенного алгоритма. Рассмотрим детально все блоки схемы на фиг. 1, выделенные пунктиром.
1. Поиск четырехугольников
На Фиг. 2 представлена блок-схема алгоритма детекции набора четырехугольников.
Рассмотрим ее этапы.
1.1. Выделение границ
Здесь и далее будем говорить, что вектор и имеет горизонтальное направление, если угол между ним и направляющим вектором горизонтального направления на изображении лежит во множестве , иначе - что он имеет преимущественно вертикальное направление. Поиск границ на изображении начинается с выполнения морфологических операций. Изображение увеличивается на δm (=5) в каждую сторону повторением граничных пикселей (Здесь и далее все параметры предложенного алгоритма, настраиваемые вручную, обозначаются греческими буквами, их значения представлены в скобках. Единицы измерения метрического расстояния совпадают с расстоянием, порождаемым сеткой размером 1 пиксель.). Затем проводится операция морфологического замыкания с размером окна ω (=3) пикселей. После этого производится размытие фильтром Гаусса с вертикальной дисперсией σe (=0.83) и нулевой горизонтальной дисперсией. На размытом изображении считается производная вдоль вертикального направления вычислением модулей разности соседних пикселей. Вышеописанная операция выполняется поканально, после чего результаты работы усредняются и получается серое изображение границ. На нем выполняется подавление немаксимумов - те пиксели, рядом с которыми есть более яркие или значение которых меньше θ (=2), зануляются, а остальные заполняются фиксированным значением. После этого ненулевые пиксели объединяются в компоненты 8-связности, содержащие не более одного пикселя в каждом столбце изображения. Такие компоненты связности далее будут называться треками. Треки фильтруются по количеству пикселей: если его длина меньше, чем ρe (=10%) от длины самого длинного трека, то все пиксели в нем также зануляются. Полученную карту горизонтальных границ обозначим Eh. Аналогично происходит детекция вертикальных границ и вводится соответствующая карта границ Ev. Карты границ Ev и Eh наложены на входное изображение на фиг. 3. а.
, иначе - что он имеет преимущественно вертикальное направление. Поиск границ на изображении начинается с выполнения морфологических операций. Изображение увеличивается на δm (=5) в каждую сторону повторением граничных пикселей (Здесь и далее все параметры предложенного алгоритма, настраиваемые вручную, обозначаются греческими буквами, их значения представлены в скобках. Единицы измерения метрического расстояния совпадают с расстоянием, порождаемым сеткой размером 1 пиксель.). Затем проводится операция морфологического замыкания с размером окна ω (=3) пикселей. После этого производится размытие фильтром Гаусса с вертикальной дисперсией σe (=0.83) и нулевой горизонтальной дисперсией. На размытом изображении считается производная вдоль вертикального направления вычислением модулей разности соседних пикселей. Вышеописанная операция выполняется поканально, после чего результаты работы усредняются и получается серое изображение границ. На нем выполняется подавление немаксимумов - те пиксели, рядом с которыми есть более яркие или значение которых меньше θ (=2), зануляются, а остальные заполняются фиксированным значением. После этого ненулевые пиксели объединяются в компоненты 8-связности, содержащие не более одного пикселя в каждом столбце изображения. Такие компоненты связности далее будут называться треками. Треки фильтруются по количеству пикселей: если его длина меньше, чем ρe (=10%) от длины самого длинного трека, то все пиксели в нем также зануляются. Полученную карту горизонтальных границ обозначим Eh. Аналогично происходит детекция вертикальных границ и вводится соответствующая карта границ Ev. Карты границ Ev и Eh наложены на входное изображение на фиг. 3. а.
1.2. Детекция прямых
После вычисления карт границ Eh и Ev происходит поиск прямых горизонтального и вертикального направления соответственно. Для вертикального направления карта границ разделяется на две (горизонтально пополам): 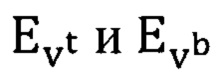 . Изображения
. Изображения  размываются при помощи фильтра Гаусса с дисперсией σh (=1) и получаются размытые карты границ
размываются при помощи фильтра Гаусса с дисперсией σh (=1) и получаются размытые карты границ 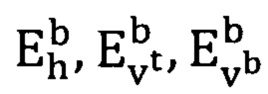 . К изображениям
. К изображениям  применяется быстрое преобразование Хафа (6). Для вертикальных границ находится глобальный максимум М на хаф-образе по обоим изображениям, после чего на каждом из них находится по νmax (=15) локальных максимумов, значения в которых составляют не менее ρ1 (=20%) от М, и в круге радиуса δ1 (=10) от которого нету более ярких локальных максимумов. Для горизонтальных границ аналогично находятся νmax локальных максимумов на изображении
применяется быстрое преобразование Хафа (6). Для вертикальных границ находится глобальный максимум М на хаф-образе по обоим изображениям, после чего на каждом из них находится по νmax (=15) локальных максимумов, значения в которых составляют не менее ρ1 (=20%) от М, и в круге радиуса δ1 (=10) от которого нету более ярких локальных максимумов. Для горизонтальных границ аналогично находятся νmax локальных максимумов на изображении  . Найденные локальные максимумы переводятся в прямые покоординатно с помощью обратного БПХ. Три множества прямых - два набора вертикальных
. Найденные локальные максимумы переводятся в прямые покоординатно с помощью обратного БПХ. Три множества прямых - два набора вертикальных  и один наборгоризонтальных прямых Lh - являются результатом работы данного этапа. На фиг. 3.б представлен результат работы данного этапа.
и один наборгоризонтальных прямых Lh - являются результатом работы данного этапа. На фиг. 3.б представлен результат работы данного этапа.
1.3. Сбор и фильтрация четырехугольников
Обозначим линию, разделяющую изображение I пополам Is. В каждой половине формируется множество четырехугольников  . Каждый четырехугольник qt формируется пересечением четырех прямых: одной горизонтальной прямой Ih ∈ Lh, прямой Is и двух вертикальных прямых
. Каждый четырехугольник qt формируется пересечением четырех прямых: одной горизонтальной прямой Ih ∈ Lh, прямой Is и двух вертикальных прямых  . Для формирования множества Qt формируются все такие возможные четырехугольники, полностью лежащие в It. Каждому четырехугольнику ставится в соответствие его контурная оценка s(qt), предложенная в (7) (ее аналог будет рассмотрен в разделе 4), после чего все четырехугольники сортируются в порядке убывания этой оценки.
. Для формирования множества Qt формируются все такие возможные четырехугольники, полностью лежащие в It. Каждому четырехугольнику ставится в соответствие его контурная оценка s(qt), предложенная в (7) (ее аналог будет рассмотрен в разделе 4), после чего все четырехугольники сортируются в порядке убывания этой оценки.
Аналогично формируется множество Qb четырехугольников, полностью лежащих в Ib.
2. Построение шестиугольников
На Фиг. 4 представлена блок-схема алгоритма формирования шестиугольников по двум четырехугольников. Рассмотрим ее этапы.
Здесь и далее под точками сгиба мы понимаем точки, в которых линия сгиба пересекает внешнюю границу документа (точка F на Фиг. 3. а)
Рассмотрим пару четырехугольников qt ∈ Qt, qb ∈ Qb. Чтобы сформировать шестиугольник, используются все отрезки этих четырехугольников, кроме тех, которые лежат на прямой Is. Можно было бы подумать, что для получения шестиугольника достаточно пересечь соответствующие вертикальные сегменты qt и qb. Однако поскольку в общем случае половины документа не плоские и их контуры не являются прямыми линиями, эти пересечения могут не соответствовать точкам сгиба (Фиг. 3. в). В связи с этим мы анализируем контуры, а не прямые. Рассмотрим карту границ Ev. Каждому вертикальному отрезку четырехугольников qt, qb ставится в соответствие трек с карты границ и рассматривается далее.
А именно, для каждого трека ev вычисляется число его пикселей на удалении не более, чем 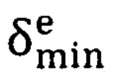 (=3) от данного отрезка s. После этого выбирается трек с наибольшим таким числом и считается соответствующим отрезку s:
(=3) от данного отрезка s. После этого выбирается трек с наибольшим таким числом и считается соответствующим отрезку s:
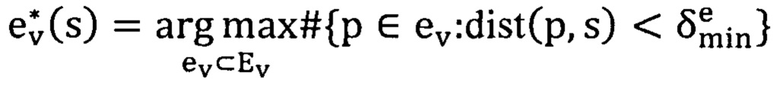
Если это число для 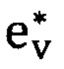 больше, чем ρmin (=50%) длины s, то такой трек считается валидным.
больше, чем ρmin (=50%) длины s, то такой трек считается валидным.
После того, как вертикальным отрезкам сопоставлены валидные треки (если были найдены), проверяется, есть ли пара вертикальных отрезков st ∈ qt, sb ∈ qb, таких что  . Будем обозначать такой
. Будем обозначать такой 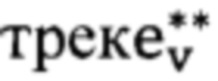 и будем говорить, что он соответствует двум вертикальным отрезкам. Если такая пара отрезков есть и с левой, и с правой стороны изображения, создается до четырех шестиугольников - вариантов положения документа - по рассматриваемой паре четырехугольников (qt, qb). Для их формирования мы используем два примитива: угол, аппроксимирующий излом границы, вызванный складыванием бумаги (раздел 2.1) и линию сгиба (раздел 2.2). Варианты определяются этими примитивами следующим образом: h1 определяется двумя углами, h2 - левым углом и линией сгиба, h3 - правым углом и линией сгиба, h4 - одной линией сгиба.
и будем говорить, что он соответствует двум вертикальным отрезкам. Если такая пара отрезков есть и с левой, и с правой стороны изображения, создается до четырех шестиугольников - вариантов положения документа - по рассматриваемой паре четырехугольников (qt, qb). Для их формирования мы используем два примитива: угол, аппроксимирующий излом границы, вызванный складыванием бумаги (раздел 2.1) и линию сгиба (раздел 2.2). Варианты определяются этими примитивами следующим образом: h1 определяется двумя углами, h2 - левым углом и линией сгиба, h3 - правым углом и линией сгиба, h4 - одной линией сгиба.
2.1. Поиск точек сгиба
Рассмотрим 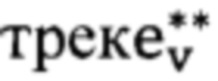 общий для двух вертикальных отрезков st, sb (например, красный трек внутри области, отмеченной пунктиром на Фиг. 3. а). Нашей целью является поиск точки сгиба (F на том же фиг.) как точки с наибольшим изломом границы.
общий для двух вертикальных отрезков st, sb (например, красный трек внутри области, отмеченной пунктиром на Фиг. 3. а). Нашей целью является поиск точки сгиба (F на том же фиг.) как точки с наибольшим изломом границы.
Чтобы найти точку сгиба, построим трехзвенную ломаную ABCD с центральным отрезком ВС и внешними отрезками АВ и CD на треке. Занумеруем точки 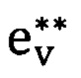 от 0 до N
от 0 до N 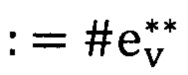 сверху вниз и обозначим индекс произвольной точки p трека
сверху вниз и обозначим индекс произвольной точки p трека  как i(p). Начиная с произвольной точки
как i(p). Начиная с произвольной точки  , построим оптимальную ломаную следующим образом. Рассмотрим произвольную точку
, построим оптимальную ломаную следующим образом. Рассмотрим произвольную точку 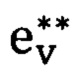 как точку В для ломаной ABCD. Сначала считая, что
как точку В для ломаной ABCD. Сначала считая, что 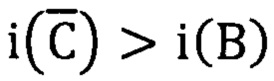 , построим кратчайший отрезок
, построим кратчайший отрезок 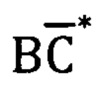 , такой, что линейная регрессия, построенная по точкам между ними, будет иметь квадратичную ошибку, превышающую εc(=0.2) и после этого возьмем точку C*, как точку, предшествующую
, такой, что линейная регрессия, построенная по точкам между ними, будет иметь квадратичную ошибку, превышающую εc(=0.2) и после этого возьмем точку C*, как точку, предшествующую 
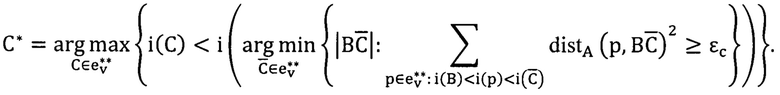
Здесь distA обозначает алгербаическое рассстояние между точкой и прямой.
обозначает алгербаическое рассстояние между точкой и прямой.
После этого, считая, что i(В) > i(А), формируется отрезок А*В максимальной длины таким образом, что аналогичная регрессия будет иметь квадратичную ошибку не более εo(=1). Аналогично, считая, что i(С*) < i(D), строится отрезок С*D* (Фиг. 3. г). Угол, соответствующий данной ломаной, строится по отрезкам А*В и С*D*, как наибольший угол между прямыми, содержащими эти отрезки. Вершиной угла является точка пересечения отрезков А*В и С*D*. Если эти прямые не пересекаются, вершиной угла считается середина отрезка ВС*.
После того, как для каждой точки  построена такая ломаная, на треке находится
построена такая ломаная, на треке находится
точка с наименьшим углом, построенным для нее. Если этот угол превосходит  (=170 градусов), то считается, что искомый излом на треке не был найден. В противном случае вершина угла является выходом алгоритма поиска точек сгиба на треке.
(=170 градусов), то считается, что искомый излом на треке не был найден. В противном случае вершина угла является выходом алгоритма поиска точек сгиба на треке.
2.2. Детекция прямой сгиба
Альтернатива h2 использует левую точку сгиба и линию сгиба, альтернатива h3 использует правую точку сгиба и линию сгиба, альтернатива h4 использует только линию сгиба. Сначала для каждого варианта опишем алгоритм определения линии сгиба, а затем - алгоритм определения координат недостающих вершин.
Линия сгиба для h2 и h3 выбирается из множества Lh, в котором содержатся все горизонтальные прямые. Искомая линия сгиба выбирается как ярчайшая (в терминах БПХ-образа) прямая среди тех прямых, которые находятся на расстоянии не более  (=15) от точки сгиба. Если прямых в окрестности рассматриваемой точки нет, то варианты h2, h3 далее не рассматриваются.
(=15) от точки сгиба. Если прямых в окрестности рассматриваемой точки нет, то варианты h2, h3 далее не рассматриваются.
Для h4 прямая сгиба находится следующим образом. Сначала вычисляются точки пересечения  прямых, содержащих горизонтальные отрезки qt и qb, с левой и правой границей изображения. Затем для каждой прямой из набора горизонтальных прямых находятся пересечения с теми же границами изображения. После чего выбираются те прямые, для которых пересечение с левой границей лежит между
прямых, содержащих горизонтальные отрезки qt и qb, с левой и правой границей изображения. Затем для каждой прямой из набора горизонтальных прямых находятся пересечения с теми же границами изображения. После чего выбираются те прямые, для которых пересечение с левой границей лежит между  на удалении хотя бы
на удалении хотя бы 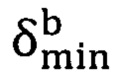 (=10) от каждого, а с правой - между
(=10) от каждого, а с правой - между  с аналогичными минимальными расстояниями от них.
с аналогичными минимальными расстояниями от них.
Из выбранных прямых выбирается та, которой соответствует самое большое значение на БПХ-образе, она и будет являться искомой линией сгиба. После этого мы рассматриваем треки (их может быть больше одного), соответствующие линии сгиба, у которых длина составляет хотя бы  (=40%) ширины изображения. Установление того, какой трек соответствует линии сгиба, производится тем же способом, что и в разделе 2. После этого для каждого такого трека проводится проверка на то, что не менее
(=40%) ширины изображения. Установление того, какой трек соответствует линии сгиба, производится тем же способом, что и в разделе 2. После этого для каждого такого трека проводится проверка на то, что не менее  (=90%) его длины лежит внутри
(=90%) его длины лежит внутри  . Если для какого-то из найденных треков это не так, то он больше не участвует в рассмотрении.
. Если для какого-то из найденных треков это не так, то он больше не участвует в рассмотрении.
После этого мы увеличиваем оставшиеся треки, добавляя β(=3) пикселя слева в той же строке изображения, что и его самая левая точка и β пикселей справа в той же строке изображения, что и его самая правая точка. После этого они пересекаются с  Если трек, общий для пары вертикальных отрезков есть и слева, и справа, то ищется пересечение с левым треком. Точка пересечения (если она нашлась) теперь рассматривается как вершина шестиугольника.
Если трек, общий для пары вертикальных отрезков есть и слева, и справа, то ищется пересечение с левым треком. Точка пересечения (если она нашлась) теперь рассматривается как вершина шестиугольника.
Для вариантов h2, h3, h4 известны пять вершин (все, кроме одной вершины на линии сгиба) и линия сгиба. Без ограничения общности предположим, что известна левая вершина. Чтобы достроить правую вершину линия сгиба пересекается с правыми вертикальными отрезками qt and qb. После этого берется середина отрезка между этими пересечениями, и она считается правой внутренней вершиной.
3. Коррекция шестиугольника для соответствия критерию неразрывности
Когда используется отображение, определяемое двумя проективными преобразованиями для того, чтобы ректифицировать шестиугольник, отвечающий внешнему контуру документа - верхняя половина проективно преобразовывается на верхнюю половину ректифицированного изображения, нижняя половина проективно преобразовывается на нижнюю половину ректифицированного изображения -существует возможность того, что текст будет разрезан в месте соединения половин (красная часть Фиг. 5).
Оказывается, для отсутствия разрыва имеет место следующий критерий. Пусть на плоскости даны два четырехугольника: A1B1CD и A2B2CD, смежные по стороне CD и лежащие в разных полуплоскостях относительно нее, и прямоугольники А1'В1'С'D' и А2'B2'С'D' со смежной стороной С'D' в разных полуплоскостях относительно нее. Пусть Н1 - проективное преобразование из A1B1CD в А1'В1'С'D', а Н2 - проективное преобразование из A2B2CD в А2'В2'С'D'. Пусть Н - преобразование, равное H1 на полуплоскости, в которой лежит A1B1CD и равное Н2 на полуплоскости, в которой лежит A2B2CD. Тогда H корректно определено тогда и только тогда, когда прямые А1В1, А2В2 и CD пересекаются в одной точке (синяя часть Фиг. 3).
Преобразуем в соответствии с критерием каждый из вариантов расположения документа. Для трех горизонтальных отрезков шестиугольника применяется алгоритм (8), вычисляющий три прямые, проходящие через одну точку и приближающие эти отрезки. После того, как были получены эти прямые, вершины шестиугольника пересчитываются: результирующие верхние и нижние прямые пересекаются с соответствующими вертикальными прямыми. Результирующая линия сгиба пересекается с верхними вертикальными отрезками. Обозначим оператор преобразования шестиугольника к модели единой горизонтальной точки схода V. Таким образом из шестиугольника h получается новый, h'=V(h).
4. Фильтрация и ранжирование шестиугольников
Для каждого шестиугольника из множества {h} вычисляется его контурная оценка, являющаяся количественной мерой яркости шестиугольника. Для этого карты границ  размываются фильтром Гаусса с дисперсией σ(=1.83). При вычислении контурной оценки рассматриваются семь отрезков: стороны шестиугольников и отрезок на линии сгиба. Для каждого из них вычисляются следующие значения: сумма пикселей pm вдоль отрезка и количество нулевых пикселей rm вдоль отрезка. Количество нулевых пикселей вдоль каждого отрезка суммируется и делится на длину всех отрезков l, в результате чего получается отношение
размываются фильтром Гаусса с дисперсией σ(=1.83). При вычислении контурной оценки рассматриваются семь отрезков: стороны шестиугольников и отрезок на линии сгиба. Для каждого из них вычисляются следующие значения: сумма пикселей pm вдоль отрезка и количество нулевых пикселей rm вдоль отрезка. Количество нулевых пикселей вдоль каждого отрезка суммируется и делится на длину всех отрезков l, в результате чего получается отношение  Также мы вычисляем значение штрафа q, предложенном в (7). Рассмотрим вершину шестиугольника vn, расположенную не на сгибе. К q добавляется сумма βp(=10) ближайших к vn пикселей, лежащих вне h вдоль сторон, пересекающихся в vn. В случае вершины, лежащей на линии сгиба vc вычисялется сумма βp(=10) ближайших к vc пикселей, лежащих вне h вдоль линии сгиба (Фиг. 3. е). Тогда контурной оценкой шестиугольника называется число
Также мы вычисляем значение штрафа q, предложенном в (7). Рассмотрим вершину шестиугольника vn, расположенную не на сгибе. К q добавляется сумма βp(=10) ближайших к vn пикселей, лежащих вне h вдоль сторон, пересекающихся в vn. В случае вершины, лежащей на линии сгиба vc вычисялется сумма βp(=10) ближайших к vc пикселей, лежащих вне h вдоль линии сгиба (Фиг. 3. е). Тогда контурной оценкой шестиугольника называется число

Из множества шестиугольников {h'} выбирается такой h'*, что

где 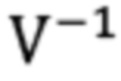 (h') - шестиугольник h, из которого h' был получен под действием оператора V, Rt(h') и Rb(h') _ соотношения сторон (9) верхней и нижней половины шестиугольника h*, вычисленные в модели камеры-обскуры с фокусным расстоянием λ(=0.705) и принципиальной точкой в центре исходного изображения, R0 - истинное соотношение сторон, равное
(h') - шестиугольник h, из которого h' был получен под действием оператора V, Rt(h') и Rb(h') _ соотношения сторон (9) верхней и нижней половины шестиугольника h*, вычисленные в модели камеры-обскуры с фокусным расстоянием λ(=0.705) и принципиальной точкой в центре исходного изображения, R0 - истинное соотношение сторон, равное  для бумаги формата А4.
для бумаги формата А4.
После этого вычисляются расстояния между соответствующими вершинами h'* и h* = 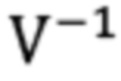 (h'*), а также углы между старыми и новыми отрезками. Если какой-то из этих углов превосходит
(h'*), а также углы между старыми и новыми отрезками. Если какой-то из этих углов превосходит 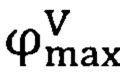 (=2.56 градусов), или какое-то из этих расстояний больше, чем
(=2.56 градусов), или какое-то из этих расстояний больше, чем  (=1%) высоты изображения, то в таком случае мы считаем, что коррекция шестиугольника при приведении его к модели единой точки схода может повредить горизонтальность текста, такой шестиугольник считается невалидным и вывод алгоритма локализации пустой.
(=1%) высоты изображения, то в таком случае мы считаем, что коррекция шестиугольника при приведении его к модели единой точки схода может повредить горизонтальность текста, такой шестиугольник считается невалидным и вывод алгоритма локализации пустой.
Необходимость такой проверки продиктована следующим. Рассмотрим Фиг. 6. На ней изображены результаты работы алгоритма на двух различных изображениях. В обоих случаях найденные шестиугольники (изображены синим на Фиг. 6. а, в) отвечают истинным расположениям документа. Однако, документа на первом изображении не соответствует модели двух плоскостей, так что шестиугольник h* сильно изменяется под действием оператора V и ректификация по скорректированному шестиугольнику h'* (изображен красным на Фиг. 6. а) неудовлетворительная (Фиг. 6. б). Документ на втором изображении соответствует модели двух плоскостей, так что шестиугольник h* (изображен зеленым на Фиг. 6. в) считается валидным и ректификация удовлетворительная (Фиг. 6. г).
5. Проективное преобразование
Если выбранный шестиугольник h'* признан невалидным, то возвращается исходное изображение. В противном случае каждая половина шестиугольника проективно преобразуется (с использованием билинейной интерполяции (10)) на соответствующую половину ректифицированного изображения (2100 × 2970). Это изображение является выходом алгоритма.
Примеры реализации способа представлены на фиг. 7 и 8.
Описанный алгоритм может быть расширен и адаптирован для локализации и проективной нормализации сложенных один раз документов с прямой сгиба, непараллельной коротким сторонам документа, пересекающей обе длинные стороны документа.
В таком случае документ на изображении может быть представлен шестиугольником и для его детекции предлагается использовать алгоритм из этапов 1 и 2.
Пусть детектирован шестиугольник h. Для того, чтобы проективно нормализовать его верхний и нижний четырехугольники, необходимо определить, в каких отношениях линия сгиба делит боковые стороны листа бумаги на ректифицированном изображении. Эти отношения могут быть вычислены при помощи алгоритма (11) восстановления образа прямоугольника на изображении, применяя его к одной из частей детектированного шестиугольника как образу прямоугольника с соотношением сторон R0(см. п. 4).
Критерий отсутствия разрыва при конкатенации образов верхнего и нижнего четырехугольников может быть переформулирован следующим образом.
Пусть на плоскости даны два четырехугольника: A1B1CD и A2B2CD, смежные по стороне CD и лежащие в разных полуплоскостях относительно нее, точка V1=А1В1  CD, точка V2=А2В2
CD, точка V2=А2В2  CD и прямоугольник А1'В1'В2'А2', разделенный прямой С'D' таким образом, что точка С' лежит на стороне А1'А2' и делит ее в отношении x1, а точка D' лежит на стороне В1'В2 и делит ее в отношении xr. Пусть Н1 - проективное преобразование из A1B1CD в А1'В1'С'D', а Н2 - проективное преобразование из A2B2CD в А2'В2'С'D'. Пусть Н - преобразование, равное Н1 на полуплоскости, в которой лежит A1B1CD и равное Н2 на полуплоскости, в которой лежит A2B2CD. Тогда Н корректно определено тогда и только тогда, когда выполняется соотношение
CD и прямоугольник А1'В1'В2'А2', разделенный прямой С'D' таким образом, что точка С' лежит на стороне А1'А2' и делит ее в отношении x1, а точка D' лежит на стороне В1'В2 и делит ее в отношении xr. Пусть Н1 - проективное преобразование из A1B1CD в А1'В1'С'D', а Н2 - проективное преобразование из A2B2CD в А2'В2'С'D'. Пусть Н - преобразование, равное Н1 на полуплоскости, в которой лежит A1B1CD и равное Н2 на полуплоскости, в которой лежит A2B2CD. Тогда Н корректно определено тогда и только тогда, когда выполняется соотношение

Данное соотношение, подобно условию существования единой точки схода в п. 3, накладывает ограничение  на взаимное расположение отрезков
на взаимное расположение отрезков 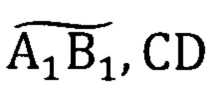 и
и  . Зафиксировав положение отрезка CD, можно найти такие
. Зафиксировав положение отрезка CD, можно найти такие  и
и  , суммарное квадратное отклонение которых от соответствующих отрезков минимально и при этом соблюдается ограничение L (существование обеспечивается тем фактом, что семейство искомых параметров двухпараметрическое, а количество накладываемых условий равно трем).
, суммарное квадратное отклонение которых от соответствующих отрезков минимально и при этом соблюдается ограничение L (существование обеспечивается тем фактом, что семейство искомых параметров двухпараметрическое, а количество накладываемых условий равно трем).
После приведения отрезков А1В1, А2В2 к соответствию критерию отсутствия разрыва при конкатенации проективно нормализованных четырехугольников предлагается применить этап 4 без учета проверки соотношения сторон в выборе лучшего шестиугольника, после чего проективно исправить лучший шестиугольник, отобразив его четырехугольники на соответствующие четырехугольники ректифицированного изображения.
Таким образом, заявленный способ позволяет достичь следующих технических результатов:
- получение изображения документов, как если бы они были отсканированы на планшетном сканере, без применения последних, с использованием лишь камеры и вычислительного устройства;
- обеспечение возможности запуска на ректифицированных изображениях сложенных пополам документов систем распознавания, предназначенных для изображений, полученных с планшетного сканера. Такие системы являются менее ресурсоемкими и легковесными, чем системы распознавания, предназначенные для фотографий;
- обеспечение возможности получения ректифицированных изображений на одном устройстве, оснащенном камерой, например, на смартфоне, что позволяет не терять время на передачу данных между устройствами. При этом не требует мощного вычислителя (видеокарты) для быстрой работы на конечных пользовательских устройствах;
- обеспечение возможности хранить и использовать физические документы, предназначенные для оцифровки системами распознавания, в сложенном пополам виде;
- обеспечение возможности отсекать случаи, когда документ на изображении не удовлетворяет модели предъявления (две плоские половины страницы формата А4);
- обеспечение возможности находить и ректифицировать документы, частично скрытые рукой. Возможность держать документ в руках при съемке значительно повышает пользовательский опыт;
- алгоритм не требует информации о заполнении документа для его геометрической нормализации.
Список литературы
(1) Michael S Brown and Brent Seales. Image restoration of arbitrarily warped documents. IEEE Transactions on pattern analysis and machine intelligence, 26(10):1295-1306, 2004.
(2) Shaodi You, Yasuyuki Matsushita, Sudipta Sinha, Yusuke Bou, and Katsushi Ikeuchi. Multiview rectification of folded documents. IEEE transactions on pattern analysis and machine intelligence, 40(2):505-511, 2017.
(3) Hao Feng, Yuechen Wang, Wengang Zhou, Jiajun Deng, and Houqiang Li. Doctr: Document image transformer for geometric unwarping and illumination correction. arXiv preprint arXiv:2110.12942, 2021.
(4) Gaofeng Meng, Chunhong Pan, Shiming Xiang, Jiangyong Duan, and Nanning Zheng. Metric rectification of curved document images. IEEE transactions on pattern analysis and machine intelligence, 34(4):707-722, 2011.
(5) Sagnik Das, Gaurav Mishra, Akshay Sudharshana, and Roy Shilkrot. The common fold: utilizing the four-fold to dewarp printed documents from a single image. In Proceedings of the 2017 ACM Symposium on Document Engineering, pages 125-128, 2017
(6) Martin L Brady. A fast discrete approximation algorithm for the radon transform. SIAM Journal on Computing, 27(1):107-119, 1998.
(7) Natalya Skoryukina, Dmitry P Nikolaev, Alexander Sheshkus, and Dmitry Polevoy. Real time rectangular document detection on mobile devices. In Seventh International Conference on Machine Vision (ICMV 2014), volume 9445, pages 458-463. SPIE, 2015.
(8) Julia Shemiakina, Ivan Konovalenko, Daniil Tropin, and Igor Faradjev. Fast projective image rectification for planar objects with manhattan structure. In Twelfth International Conference on Machine Vision (ICMV 2019), volume 11433, pages 450-458. SPIE, 2020.
(9) Zhengyou Zhang and Li-Wei He. Whiteboard scanning and image enhancement. Digital signal processing, 17(2):414-132, 2007.
(10) Anton Trusov and Elena Limonova. The analysis of projective transformation algorithms for image recognition on mobile devices. In Twelfth International Conference on Machine Vision (ICMV 2019), volume 11433, pages 250-257. SPIE, 2020.
(11) Daniil V. Tropin, Ivan A. Konovalenko, Natalya S. Skoryukina, Dmitry P. Nikolaev and Vladimir V. Arlazarov. Improved algorithm of ID card detection by a priori knowledge of the document aspect ratio. In Thirteenth International Conference on Machine Vision (ICMV 2020), volume 11605, pages 407-415. SPIE, 2021.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения копии документа по цветному изображению документа | 2024 |
|
RU2840263C1 |
| Способ измерения дальности до вагона на прямолинейном участке железнодорожного пути | 2021 |
|
RU2769453C1 |
| Способ измерения дальности до вагона с помощью видеокамеры | 2023 |
|
RU2811525C1 |
| Способ детектирования голографической защиты на документах в видеопотоке | 2021 |
|
RU2771005C1 |
| Способ валидации ответов систем локализации и идентификации документов с помощью глобальных особенностей | 2023 |
|
RU2826893C1 |
| Способ поиска машиночитаемой зоны документа на изображении с помощью ИНС, содержащей прямое и транспонированное преобразования Хафа | 2024 |
|
RU2833293C1 |
| Способ определения (распознавания) факта предъявления цифровой копии документа в виде пересъемки экрана | 2021 |
|
RU2774058C1 |
| Способ измерения дальности от маневрового тепловоза до вагона на прямолинейном участке железнодорожного пути | 2020 |
|
RU2750364C1 |
| Способ детектирования пальцев на изображениях документов, снятых в неконтролируемых условиях | 2024 |
|
RU2831508C1 |
| СПОСОБ И УСТРОЙСТВО ОБРАБОТКИ СТЕРЕОИЗОБРАЖЕНИЙ | 2016 |
|
RU2623806C1 |




Изобретение относится к области обработки оцифрованных документов. Технический результат заключается в повышении качества развертки сложенных документов с устойчивостью к окклюзии края документа. Технический результат достигается тем, что верхняя половина изображения содержит большую часть верхней половины документа, а нижняя половина изображения содержит большую часть нижней половины документа, при этом высота больше ширины, при этом исходное изображение I делится пополам на верхнюю часть It и нижнюю часть Ib, строится грубое приближение половин документа двумя четырехугольниками, для этого к обеим половинам применяется алгоритм локализации четырехугольников, основанный на детекции границ и прямых, выходом которого является набор четырехугольников, отсортированных по их контурной оценке, таким образом получается множество четырехугольников Qt, расположенных на It, и множество четырехугольников Qb, расположенных на Ib, при этом каждая пара четырехугольников используется для того, чтобы составить шестиугольник, который бы представлял внешние границы сложенного документа на изображении, к каждому сформированному и уточненному шестиугольнику применяется алгоритм коррекции, после этого шестиугольники сортируются по их контурной оценке. 27 ил.
Способ получения ректифицированных изображений документов, сложенных пополам, заключающийся в поступлении на вход модели предъявления документа, причем верхняя половина изображения содержит большую часть верхней половины документа, а нижняя половина изображения содержит большую часть нижней половины документа, при этом высота больше ширины, отличающийся тем, что исходное изображение I делится пополам на верхнюю часть It и нижнюю часть Ib, строится грубое приближение половин документа двумя четырехугольниками, для этого к обеим половинам применяется алгоритм локализации четырехугольников, основанный на детекции границ и прямых, выходом которого является набор четырехугольников, отсортированных по их контурной оценке, таким образом получается множество четырехугольников Qt, расположенных на It, и множество четырехугольников Qb, расположенных на Ib, при этом каждая пара четырехугольников используется для того, чтобы составить шестиугольник, который бы представлял внешние границы сложенного документа на изображении, к каждому сформированному и уточненному шестиугольнику применяется алгоритм коррекции, после этого шестиугольники сортируются по их контурной оценке и тот, у которого самая высокая контурная оценка, является выходом из этапа локализации, последним этапом является отображение входного изображения, определяемого двумя проективными преобразованиями.
| СПОСОБ И СИСТЕМА ИСПРАВЛЕНИЯ ПЕРСПЕКТИВНЫХ ИСКАЖЕНИЙ В ИЗОБРАЖЕНИЯХ, ЗАНИМАЮЩИХ ДВУХСТРАНИЧНЫЙ РАЗВОРОТ | 2016 |
|
RU2631765C1 |
| US 20170076169 A1, 16.03.2017 | |||
| US 10991081 B1, 27.04.2021 | |||
| CN 111353961 A, 30.06.2020 | |||
| US 7463772 B1, 09.12.2008. | |||
Авторы
Даты
2024-06-07—Публикация
2023-11-24—Подача