Изобретение относится к спинтронике, более конкретно к спиновым полупроводниковым наногетероструктурам, используемым для изготовления СВЧ спиновых гетеротранзисторов на квантовых точках, монолитных интегральных схем, а также элементов спиновой памяти и логики с различными способами управления спиновым током, с улучшенными энергетическими параметрами, частотными характеристиками и быстродействием, устойчивым спиновым переносом тока и увеличенным диапазоном рабочих температур.
Известен аналог «Электронный аналог электрооптического модулятора» [Supriyo Datta and Biswajit Das, Electronic analog of the electro-optic modulator, Appl. Phys. Lett, v. 56, №7, p. 665-667, 1990], в котором рассмотрена возможность разработки спинового полевого транзистора, основанного на релятивистском эффекте. Спиновый полевой транзистор содержит ферромагнитные исток и сток, а также полупроводниковый затвор. В случае баллистического (без рассеяния) переноса носителей с субрелятивистской дрейфовой скоростью около 1% от скорости света в вакууме (vdr≥3⋅106 м/с) в соответствии с теорией электромагнитного поля у движущегося электрона появляется эффективное магнитное поле, изменяющее направление спинов электронов, что приводит к изменению плотности спин-поляризованного тока в канале спинового транзистора. Прецессия спина возникает вследствие спин-орбитального взаимодействия и с учетом приложенного напряжения затвора. С помощью напряжения затвора можно управлять величиной тока спинового транзистора.
Недостатком аналога является отсутствие причинно-следственной связи состава ферромагнитного материала транзистора с субрелятивистской скоростью дрейфа носителей, а также с температурой Кюри ферромагнетика. Другим недостатком аналога является отсутствие аналитического выражения для спин-поляризованного тока, который должен включать спиновую и орбитальную составляющие тока, быть инвариантным релятивистским преобразованиям Лоренца и матрице вращательных преобразований волновых функций (спиноров).
При установлении причинно-следственной связи состава ферромагнитного материала спин полевого транзистора Датта-Даса с субрелятивистской скоростью дрейфа носителей vdr следует обратить внимание на температуру Кюри, при которой области спонтанного намагничения распадаются и материал утрачивает свои ферромагнитные свойства.
Согласно уровню науки и техники при достижении температуры Кюри (Тс) тепловая скорость электронов ферромагнитного материала значительно возрастает до значения

где k - постоянная Больцмана;
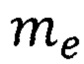 - масса электрона. Температура Кюри находится по формуле [Р. Фейнман, Р. Лейтон, М. Сэндс.Фейнмановские лекции по физике. Т. 7. Физика сплошных сред. - М.: Мир, 1977, 287 с. С. 157]
- масса электрона. Температура Кюри находится по формуле [Р. Фейнман, Р. Лейтон, М. Сэндс.Фейнмановские лекции по физике. Т. 7. Физика сплошных сред. - М.: Мир, 1977, 287 с. С. 157]

где 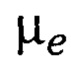 - спиновый магнитный момент электрона,
- спиновый магнитный момент электрона, 
е - электрический заряд электрона;
 - постоянная Планка;
- постоянная Планка;
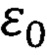 - электрическая постоянная;
- электрическая постоянная;
с - скорость света в вакууме;
N - число, зависящее от плотности и атомной массы вещества,
N = плотность • N/атомная масса;
NA - число Авогадро;
λ - подгоночный параметр (постоянная молекулярного поля Вейсса).
Постоянная λ - величина неизвестная. Однако известно, что магнитное взаимодействие между движущимися зарядами является релятивистским эффектом. При этом магнитная сила слабее кулоновской на множитель 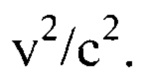 Очевидно, что при соотношении
Очевидно, что при соотношении  материал утрачивает свои ферромагнитные свойства, а для соотношения
материал утрачивает свои ферромагнитные свойства, а для соотношения 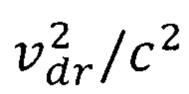 ферромагнитные свойства материала восстанавливаются. На основании изложенного выше полагаем
ферромагнитные свойства материала восстанавливаются. На основании изложенного выше полагаем

В частном случае  , где
, где 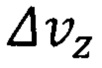 - неопределенность скорости электрона на внешней орбите атома ферромагнитного вещества группы железа с порядковым номером Z Периодической системы элементов. Неопределенность скорости
- неопределенность скорости электрона на внешней орбите атома ферромагнитного вещества группы железа с порядковым номером Z Периодической системы элементов. Неопределенность скорости 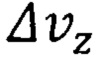 находится следующим образом. Согласно микроскопических флуктуационных подходов уравнение движения электрона в центральном поле для случая отрицательного собственного значения энергии Е имеет вид [Плахотник А.С. Электронные приборы сверхвысокой частоты. Классические и микроскопические флуктуационные методы повышения энергетических и качественных показателей: монография. - Владивосток: ТОВМИ им. СО. Макарова ВУНЦ ВМФ «ВМА», 2011, 220 с. С. 207-209; Плахотник А.С.Основы микроскопической флуктуационной теории. Избранные труды Всероссийской конференции по проблемам науки и технологий. - Москва.: РАН, 2011, 154 с. С. 122-123; патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл.№8]:
находится следующим образом. Согласно микроскопических флуктуационных подходов уравнение движения электрона в центральном поле для случая отрицательного собственного значения энергии Е имеет вид [Плахотник А.С. Электронные приборы сверхвысокой частоты. Классические и микроскопические флуктуационные методы повышения энергетических и качественных показателей: монография. - Владивосток: ТОВМИ им. СО. Макарова ВУНЦ ВМФ «ВМА», 2011, 220 с. С. 207-209; Плахотник А.С.Основы микроскопической флуктуационной теории. Избранные труды Всероссийской конференции по проблемам науки и технологий. - Москва.: РАН, 2011, 154 с. С. 122-123; патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл.№8]:

где  - постоянная Планка;
- постоянная Планка;
 - волновая функция;
- волновая функция;
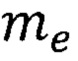 - масса элементарного заряда;
- масса элементарного заряда;
 - оператор Лапласа;
- оператор Лапласа;
Е - собственное значение энергии электрона;
е - заряд электрона;
V(r) - заданная функция, зависящая только от радиуса и определяющая потенциал поля, 
r - радиус траектории движения заряда;
Z - атомный номер;
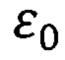 - диэлектрическая постоянная;
- диэлектрическая постоянная;
N - некоторое действительное число.
В радиальных волновых функциях формула (4) принимает вид
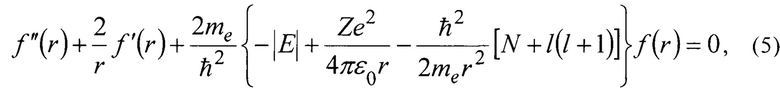
где  - радиальная волновая функция;
- радиальная волновая функция;
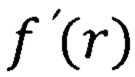 - первая производная радиальной волновой функции;
- первая производная радиальной волновой функции;
 - вторая производная радиальной волновой функции. Решение уравнения (5) дает собственные значения энергии электрона
- вторая производная радиальной волновой функции. Решение уравнения (5) дает собственные значения энергии электрона
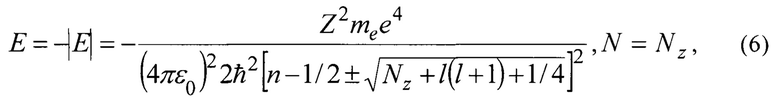
где n - главное квантовое число;
 - орбитальное квантовое число;
- орбитальное квантовое число;
Nz - параметр флуктуации.
Находим параметр флуктуации Nz, приравнивая одно из решений (6) потенциалу ионизации Ez атома элемента Периодической системы,
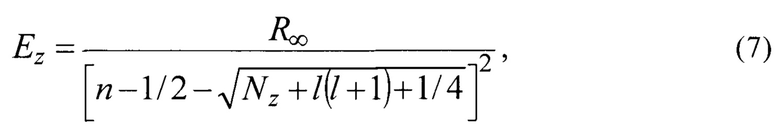
где 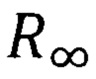 - постоянная Ридберга,
- постоянная Ридберга, 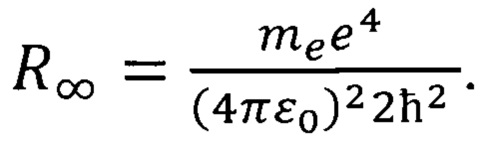
С учетом параметра флуктуации Nz рассчитываем неопределенность скорости электрона на внешней орбите атома любого элемента

где rz - радиус атома с атомным номером Z.
Результатом решения уравнения (7) являются два значения параметра флуктуации 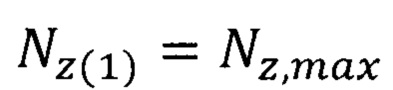 и
и  , то есть
, то есть 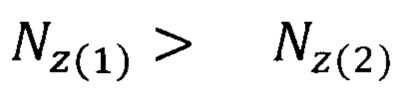 .
.
Соответственно различаются и неопределенности скорости электрона

В формуле (3) для нахождения подгоночного параметра используется неопределенность скорости электрона (10)
используется неопределенность скорости электрона (10) 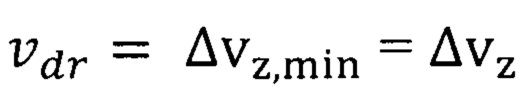 . Подставив в формулу (2) значение параметра λ формула (3) и тепловую скорость
. Подставив в формулу (2) значение параметра λ формула (3) и тепловую скорость  формула (1), получим теоретическое значение температуры Кюри
формула (1), получим теоретическое значение температуры Кюри

где П - некоторая постоянная, 

В частном случае 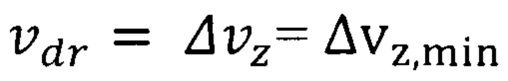 - минимальная неопределенность скорости электрона формула (10).
- минимальная неопределенность скорости электрона формула (10).
Установим причинно-следственную связь некоторых простых ферромагнитных материалов группы железа, скорости дрейфа обобщенных электронов в их кристаллах и температуры Кюри ферромагнетиков.
Исходные данные сведены в таблицы №1 и №2. Кроме того в табл. 1 представлены расчеты параметров флуктуации  по формуле (7).
по формуле (7).

В табл. 2 также представлены исходные данные и расчеты числа N для железа, кобальта и никеля.

Формулы (8), (9) и (10) справедливы при расчете неопределенности скорости  для электрона внешней орбиты свободного атома. При вычислении параметра
для электрона внешней орбиты свободного атома. При вычислении параметра  обобществленного электрона в кристалле металла ферромагнетика по формуле (10) необходимо находить некоторое среднее значение радиуса с учетом не только радиуса атома
обобществленного электрона в кристалле металла ферромагнетика по формуле (10) необходимо находить некоторое среднее значение радиуса с учетом не только радиуса атома 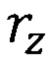 , но также и радиуса иона
, но также и радиуса иона  параметра решетки
параметра решетки 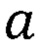 и расстояния
и расстояния  , иллюстрирующего состояние устойчивого равновесия атомов, образующих кристалл.
, иллюстрирующего состояние устойчивого равновесия атомов, образующих кристалл.
Пример 1. Для никеля расстояние  устойчивого равновесия атомов вычисляем по формуле
устойчивого равновесия атомов вычисляем по формуле

Подставив численные значения параметров 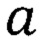 и
и 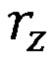 из табл. 1, получим
из табл. 1, получим 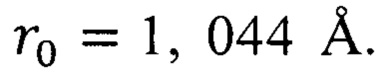 Поскольку
Поскольку  то используем среднее квадратичное значение радиуса атома по формуле
то используем среднее квадратичное значение радиуса атома по формуле

где  - радиус атома;
- радиус атома;
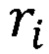 - радиус иона;
- радиус иона;
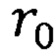 - расстояние устойчивого равновесия атомов.
- расстояние устойчивого равновесия атомов.
С учетом численных значений параметров  и
и  табл. 1, а также вычисленного значения расстояния
табл. 1, а также вычисленного значения расстояния 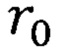 , получим по формуле (13)
, получим по формуле (13)

Неопределенность скорости обобществленного электрона в кристалле никеля находим по формуле (10) с учетом замены радиуса 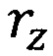 на
на 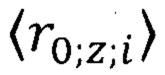
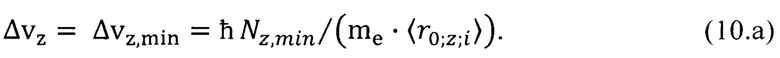
По формуле (10.а) с учетом параметра 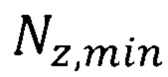 для никеля табл. 1 находим неопределенность скорости
для никеля табл. 1 находим неопределенность скорости 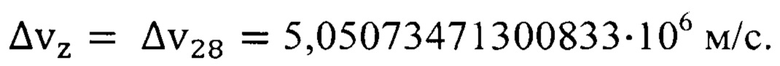
По формуле (11) с учетом числа N для никеля табл.2 и найденного значения 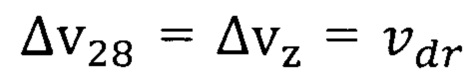 получим теоретическое значение температуры Кюри
получим теоретическое значение температуры Кюри 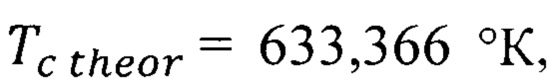 которое с погрешностью 0,37% соответствует
которое с погрешностью 0,37% соответствует 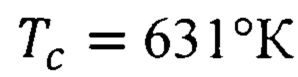 никеля табл. 2.
никеля табл. 2.
Пример 2. Для железа расстояние  устойчивого равновесия атомов, вычисленного по формуле (12), равно
устойчивого равновесия атомов, вычисленного по формуле (12), равно 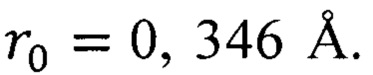 Поскольку
Поскольку  то вычисляем параметр
то вычисляем параметр  по формуле
по формуле

Подставив численные значения параметров 
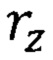 и
и 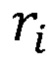 из табл. 1, получим
из табл. 1, получим 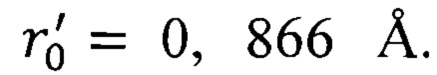 Находим среднее арифметическое значение радиуса по формуле
Находим среднее арифметическое значение радиуса по формуле

Расчет по формуле (15) дает 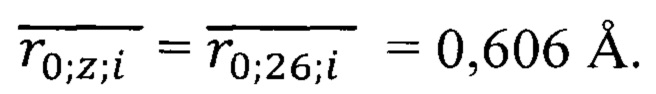
Неопределенность скорости обобществленного электрона в кристалле железа находим по формуле (10) с учетом замены радиуса  на
на 
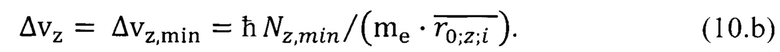
По формуле (10.b) с учетом параметра  для железа табл. 1 находим неопределенность скорости
для железа табл. 1 находим неопределенность скорости 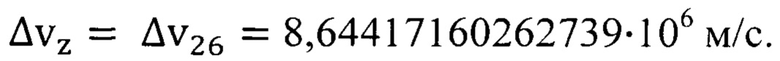
По формуле (11) с учетом числа N для железа табл. 2 и найденного значения 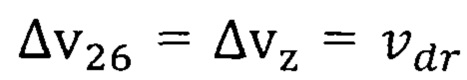 получим теоретическое значение температуры Кюри
получим теоретическое значение температуры Кюри 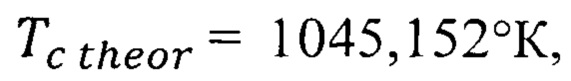 которое с погрешностью 0,21% соответствует
которое с погрешностью 0,21% соответствует  железа табл. 2.
железа табл. 2.
Пример 3. Для кобальта расстояние  устойчивого равновесия атомов, вычисленное по формуле (12), равно
устойчивого равновесия атомов, вычисленное по формуле (12), равно 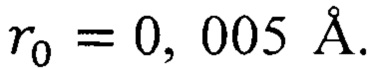 Поскольку
Поскольку  то вычисляем среднее квадратичное значение радиуса атома по формуле
то вычисляем среднее квадратичное значение радиуса атома по формуле

Подставив численные значения параметров  и
и  из табл. 1, получим
из табл. 1, получим 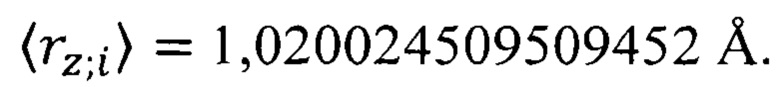 И далее находим параметр
И далее находим параметр 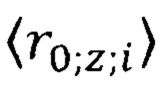

С учетом значения параметра 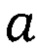 решетки кобальта табл. 1 находим по формуле (17) параметр
решетки кобальта табл. 1 находим по формуле (17) параметр  По формуле (10.а) с учетом параметра
По формуле (10.а) с учетом параметра  для кобальта табл. 1 находим неопределенность скорости
для кобальта табл. 1 находим неопределенность скорости 
По формуле (11) с учетом числа N для кобальта табл.2 и найденного значения  получим теоретическое значение температуры Кюри
получим теоретическое значение температуры Кюри  которое с погрешностью 0,98% соответствует
которое с погрешностью 0,98% соответствует  железа табл. 2. Расчеты в примерах 1-3 сведены в табл. 3.
железа табл. 2. Расчеты в примерах 1-3 сведены в табл. 3.

Различия в расчетах средних значений радиусов объясняются значительной разницей в температурах Кюри и других физических свойств ферромагнитных материалов группы железа, например магнитострикции. Пример 4. Для пермаллоя 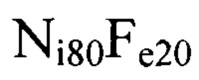 взаимное влияние атомов и решеток никеля и железа учитываем через среднее квадратичное значение радиуса
взаимное влияние атомов и решеток никеля и железа учитываем через среднее квадратичное значение радиуса

Средние значения радиусов атома железа 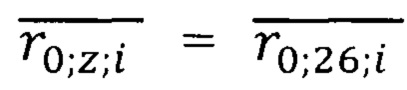 и никеля
и никеля  представлены в табл. 3. Расчет по формуле (18) дает значение
представлены в табл. 3. Расчет по формуле (18) дает значение 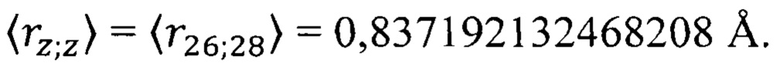
Неопределенность скорости обобществленного электрона в кристалле никеля и железа находим по формуле (10) с учетом замены радиуса  на
на 
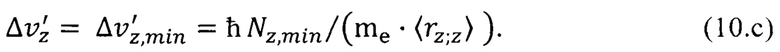
На основании формулы (10.с) с учетом параметров 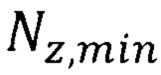 для железа и никеля табл.1 находим соответствующие неопределенности скорости
для железа и никеля табл.1 находим соответствующие неопределенности скорости  и
и 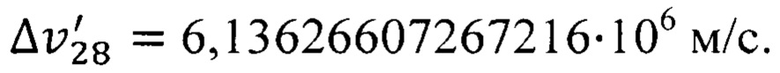
В результате для пермаллоя скорость дрейфа обобществленных электронов определяется по формуле

С учетом численных значений параметров 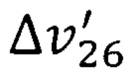 и
и 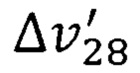 по формуле (19) получим
по формуле (19) получим  Скорость дрейфа электронов для пермаллоя примерно соответствует 2% от скорости света в вакууме. Число N для пермаллоя вычисляется по формуле
Скорость дрейфа электронов для пермаллоя примерно соответствует 2% от скорости света в вакууме. Число N для пермаллоя вычисляется по формуле

С учетом численных значений 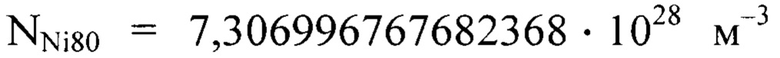 и
и 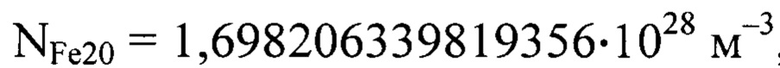 , которые вычислены на основании данных табл.2, по формуле (20) получим
, которые вычислены на основании данных табл.2, по формуле (20) получим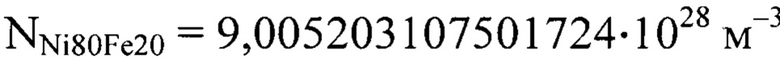
По формуле (11) с учетом числа  и найденного численного значения дрейфовой скорости для пермаллоя, получим теоретическое значение температуры Кюри
и найденного численного значения дрейфовой скорости для пермаллоя, получим теоретическое значение температуры Кюри  которое с погрешностью 0,38% (по модулю) соответствует
которое с погрешностью 0,38% (по модулю) соответствует  пермаллоя табл. 4.
пермаллоя табл. 4.

Тем самым установлена причинно-следственная связь состава ферромагнитного материала спин полевого транзистора Датта-Даса с субрелятивистской скоростью дрейфа носителей, а также с температурой Кюри ферромагнетика.
Другим недостатком спин полевого транзистора Датта-Даса является отсутствие аналитического выражения для спин-поляризованного тока, который должен включать спиновую и орбитальную составляющие тока, быть инвариантным релятивистским преобразованиям Лоренца и матрице вращательных преобразований волновых функций (спиноров).
Согласно уровню науки и техники в релятивистской теории плотность тока (электрона) во внешнем поле выражается в общем виде через векторный (и скалярный) потенциал и волновую функцию [В.Б. Берестецкий, Е.М. Лифшиц, Л.П. Питаевский. Теоретическая физика. Т. 4. Квантовая электродинамика. - М.: Наука, 1989, 723 с. С. 151], что согласуется с выражением для плотности тока из нерелятивистской теории [Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика. Т. 3. Квантовая механика. Нерелятивистская теория. - М.: Наука, 1974, 752 с. С.539]. В обоих выражениях используются разложения по степеням (1/с) и поэтому указанные плотности тока не являются инвариантными преобразованиям Лоренца. В отмеченных выражениях также нет свидетельств о спиновой и орбитальной составляющей тока. В то же время известны, например, потенциалы Льенара и Вихерта, представленные в релятивистском виде и инвариантные преобразованиям Лоренца [Р. Фейнман, Р. Лейтон, М. Сэндс.Фейнмановские лекции по физике. Т. 6. Электродинамика. - М.: Мир, 1977, 347 с. С. 165]. В ряде работ можно найти выражения для плотности тока, в которых имеет место учет только спиновой составляющей тока [M.J. Majid, С.С. Савинский. Особенности временной эволюции локализованных квантовых состояний в графене. // ФТП, 2012, т. 46, вып. 12, с. 1576 - 1580. С. 1577; С.А. Тарасенко, А.В. Пошакинский, Е.Л. Ивченко, И. Степанов, М. Эрсфельд, М. Лепса, Б.Бешотен. Эффект дрожащего движения электронов с расщепленными по спину состояниями. // Письма в ЖЭТФ, 2018, т. 108, вып.5, с. 348-351. С. 350]. Установлено, что движение даже свободного электрона носит сложный характер, поскольку скорость электрона приобретает самостоятельное значение наряду с его импульсом, а движение электрона не является в общем случае «прямолинейным». Еще Шредингер показал, что причиной таких особенностей является наличие у электрона внутренней структуры, которая определяется его спиновым моментом [Г.Ф. Ефремов, Д.А. Петров. О характере движения электрона Дирака в постоянном магнитном поле. Вестник Нижегородского университета им. Н.И. Лобачевского, 2011, №2(1), с. 170-180. С. 170].
Для устранения другого недостатка спин полевого транзистора Датта-Даса воспользуемся формулой вещественной части плотности тока элементарного заряда в одномерном виде [Плахотник А.С.Электронные приборы сверхвысокой частоты. Классические и микроскопические флуктуационные методы повышения энергетических и качественных показателей: монография. - Владивосток: ТОВМИ им. СО. Макарова ВУНЦ ВМФ «ВМА», 2011, 220 с. С 110; Плахотник А.С Основы микроскопической флуктуационной теории. Избранные труды Всероссийской конференции по проблемам науки и технологий. - Москва.: РАН, 2011, 154 с. С. 45]

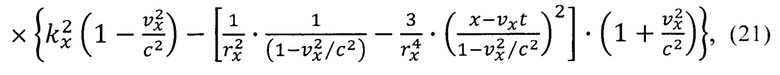
где 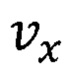 - проекция скорости заряда на ось х;
- проекция скорости заряда на ось х;
е - элементарный электрический заряд;
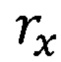 - проекция радиуса-вектора движения заряда на ось х;
- проекция радиуса-вектора движения заряда на ось х;
kx - проекция волнового вектора на ось х, 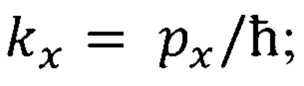
рх - проекция импульса частицы на ось х;
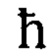 - постоянная Планка.
- постоянная Планка.
В формуле (21) множитель вида  относится к преобразованиям Лоренца, геометрический смысл которых заключается в повороте инерциальной системы отсчета на мнимый угол. Множитель вида
относится к преобразованиям Лоренца, геометрический смысл которых заключается в повороте инерциальной системы отсчета на мнимый угол. Множитель вида 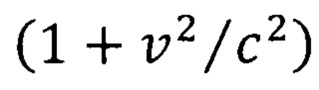 относится к новым преобразованиям [Плахотник А.С. О причинности во втором постулате специальной теории относительности. // 28-я научно-техническая конференция. Тезисы докладов. - Владивосток: ТОВВМУ им. С.О. Макарова, 1984, с. 7-10. С. 10; Плахотник А.С. Электронные приборы сверхвысокой частоты. Классические и микроскопические флуктуационные методы повышения энергетических и качественных показателей: монография. - Владивосток: ТОВМИ им. СО. Макарова ВУНЦ ВМФ «ВМА», 2011, 220 с. С. 112; Плахотник А.С. Основы микроскопической флуктуационной теории. Избранные труды Всероссийской конференции по проблемам науки и технологий. - Москва.: РАН, 2011, 154 с. С 67]
относится к новым преобразованиям [Плахотник А.С. О причинности во втором постулате специальной теории относительности. // 28-я научно-техническая конференция. Тезисы докладов. - Владивосток: ТОВВМУ им. С.О. Макарова, 1984, с. 7-10. С. 10; Плахотник А.С. Электронные приборы сверхвысокой частоты. Классические и микроскопические флуктуационные методы повышения энергетических и качественных показателей: монография. - Владивосток: ТОВМИ им. СО. Макарова ВУНЦ ВМФ «ВМА», 2011, 220 с. С. 112; Плахотник А.С. Основы микроскопической флуктуационной теории. Избранные труды Всероссийской конференции по проблемам науки и технологий. - Москва.: РАН, 2011, 154 с. С 67]
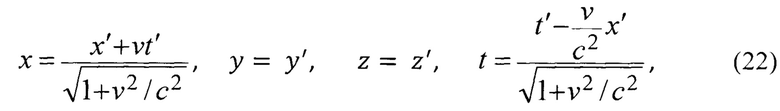
где х, y, z, t - координаты событий в системе отсчета К;
х', у', z', t' - координаты тех же событий в системе отсчета К'.
Геометрическая интерпретация преобразований (22) означает поворот системы отсчета на вещественный угол. Поскольку преобразования (22) иллюстрируют переходы вращающейся системы отсчета (например, спин электрона), то они инвариантны матрице вращательных преобразований волновых функций (спиноров) [Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика. Т. 3. Квантовая механика. Нерелятивистская теория. - М.: Наука, 1974, 752 с. С. 256].
В частном случае формулу (21) можно записать с учетом неопределенности скорости электрона 

В фигурных скобках формулы (23) представлен квадрат полного механического момента электрона. При получении формулы (23) в формуле (21) использовано соотношение

где 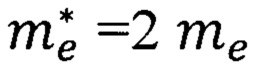 - эффективная масса электрона на внешней орбите свободного атома любого элемента Периодической системы [патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8].
- эффективная масса электрона на внешней орбите свободного атома любого элемента Периодической системы [патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8].
Плотность тока (23) содержит спиновую и орбитальную составляющие, инвариантна преобразованиям Лоренца и матрице вращательных преобразований волновых функций (спиноров), что и требовалось доказать.
Собственный механический момент электрона (спин) в формуле (23) имеет вид

Точность расчетов по формуле (25), а значит и по формулам (21), (23), можно проверить, вычислив, например, аномальный магнитный момент электрона в атоме водорода по релятивистской формуле

где  - магнетон Бора;
- магнетон Бора;
 - максимальное значение неопределенности скорости электрона на внешней орбите атома водорода.
- максимальное значение неопределенности скорости электрона на внешней орбите атома водорода.
С этой целью уточняем параметры флуктуации энергии атома водорода для квантовых состояний n=1; n=2; n-2-j (j=1/2), используя формулы [Плахотник А.С. Основы микроскопической флуктуационной теории. Избранные труды Всероссийской конференции по проблемам науки и технологий. - Москва.: РАН, 2011, 154 с. С. 82]
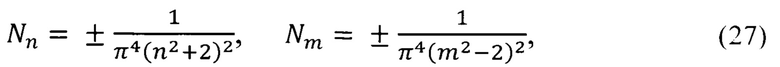
где π=3,141592653589793.
С учетом n=m=1; 2; 2-1/2 получим следующие параметры флуктуации энергии атома водорода  (сравни с поправками Ридберга [Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика. Т. 3. Квантовая механика. Нерелятивистская теория. - М.: Наука, 1974, 752 с. С. 298])
(сравни с поправками Ридберга [Л.Д. Ландау, Е.М. Лифшиц. Теоретическая физика. Т. 3. Квантовая механика. Нерелятивистская теория. - М.: Наука, 1974, 752 с. С. 298])

Для расчета максимального значения неопределенности скорости электрона 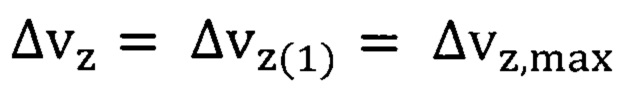 необходимо рассчитать параметр флуктуации
необходимо рассчитать параметр флуктуации 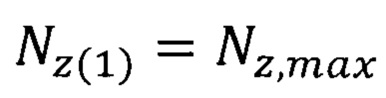 и уточнить радиус
и уточнить радиус 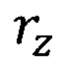 атома водорода. Расчет параметра флуктуации
атома водорода. Расчет параметра флуктуации 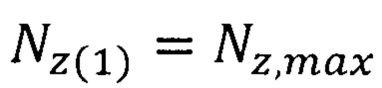 производим, приравнивая решение формула (7) к энергии возбуждения
производим, приравнивая решение формула (7) к энергии возбуждения  для n=2 (в эффекте Лэмба
для n=2 (в эффекте Лэмба  [У.Е. Лэмб, Р.К. Ризерфорд. Тонкая структура водородного атома. // УФН, 1951, т. 45, вып4, с. 553 -615. С. 564])
[У.Е. Лэмб, Р.К. Ризерфорд. Тонкая структура водородного атома. // УФН, 1951, т. 45, вып4, с. 553 -615. С. 564])
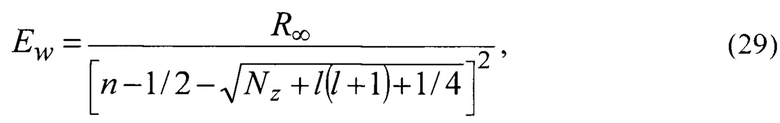
где 
 - энергия ионизации атома водорода,
- энергия ионизации атома водорода,  [X. Кухлинг. Справочник по физике. - М.: Мир, 1982, 519 с. С. 420];
[X. Кухлинг. Справочник по физике. - М.: Мир, 1982, 519 с. С. 420];
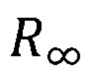 - постоянная Ридберга,
- постоянная Ридберга, 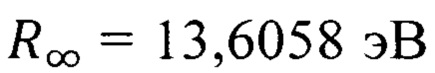 [X. Кухлинг. Справочник по физике. -М.: Мир, 1982, 519 с. С. 418].
[X. Кухлинг. Справочник по физике. -М.: Мир, 1982, 519 с. С. 418].
В результате решения уравнения (29) получим для состояния 2р атома водорода (n=2, 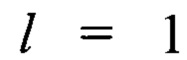 ) следующее значение параметра флуктуации
) следующее значение параметра флуктуации 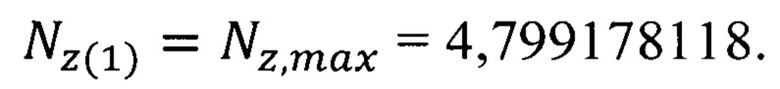
Уточнение радиуса  атома водорода выполняем с помощью параметров формула (28). С учетом того, что в случае водородного атома состояние 2р разрушается и атом переходит в состояние Is с излучением фотона в течение 1,595⋅10-9 с [У.Е. Лэмб, Р.К. Ризерфорд. Тонкая структура водородного атома. // УФН, 1951, т. 45, вып 4, с. 553-615. С .559], за основу берем радиус n=1 орбиты атома водорода
атома водорода выполняем с помощью параметров формула (28). С учетом того, что в случае водородного атома состояние 2р разрушается и атом переходит в состояние Is с излучением фотона в течение 1,595⋅10-9 с [У.Е. Лэмб, Р.К. Ризерфорд. Тонкая структура водородного атома. // УФН, 1951, т. 45, вып 4, с. 553-615. С .559], за основу берем радиус n=1 орбиты атома водорода  Уточненный радиус рассчитываем по формуле
Уточненный радиус рассчитываем по формуле

В формуле (30) параметр  определяется по формуле
определяется по формуле
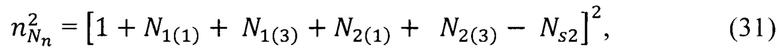
где 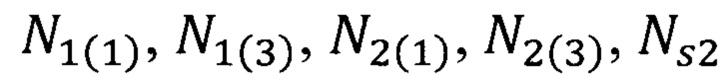 - параметры из формулы (28).
- параметры из формулы (28).
Расчет по формуле (31) дает значение 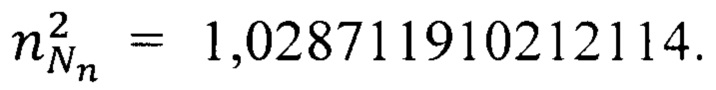 В результате по формуле (30) получим
В результате по формуле (30) получим 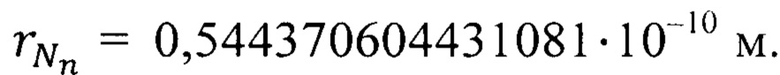 На основании формулы (9) с учетом параметра флуктуации
На основании формулы (9) с учетом параметра флуктуации 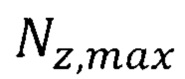 для квантового состояния 2р атома водорода и радиуса атома
для квантового состояния 2р атома водорода и радиуса атома 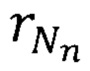 находим неопределенность скорости электрона
находим неопределенность скорости электрона 
На основании формулы (26) с учетом равенства 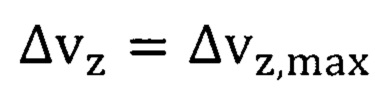 получим соотношение
получим соотношение  которое гораздо точнее результатов в квантовой электродинамике, полученных путем сложных вычислений [В.Б. Берестецкий, Е.М. Лифшиц, Л.П. Питаевский. Теоретическая физика. Т. 4. Квантовая электродинамика. - М.: Наука, 1989, 723 с. С. 582; П. Каш. Магнитный момент электрона. // УФН, т.93, вып.1, с. 159-175. С. 174]. Более того, при вычислении параметра
которое гораздо точнее результатов в квантовой электродинамике, полученных путем сложных вычислений [В.Б. Берестецкий, Е.М. Лифшиц, Л.П. Питаевский. Теоретическая физика. Т. 4. Квантовая электродинамика. - М.: Наука, 1989, 723 с. С. 582; П. Каш. Магнитный момент электрона. // УФН, т.93, вып.1, с. 159-175. С. 174]. Более того, при вычислении параметра  по формуле
по формуле
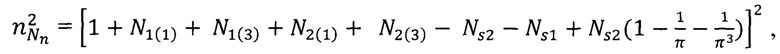 (32) получим соотношение
(32) получим соотношение 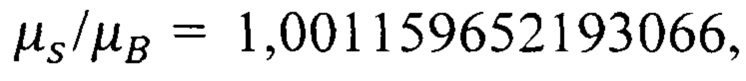 погрешность которого к экспериментальному значению аномального магнитного момента электрона в атоме водорода
погрешность которого к экспериментальному значению аномального магнитного момента электрона в атоме водорода 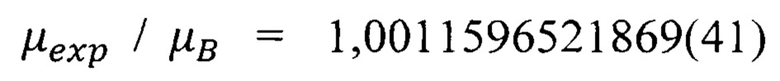 составляет примерно 6,1174⋅10-10 %, что более чем в восемь раз превышает известную на данный момент точность расчета в квантовой электродинамике (1978 год)
составляет примерно 6,1174⋅10-10 %, что более чем в восемь раз превышает известную на данный момент точность расчета в квантовой электродинамике (1978 год)  [wikipedia.org/wiki Лэмбовский сдвиг]. Выполненные расчеты подтверждают, что формулы (23), (25) и (26) отличаются высокой точностью и важны при расчете спиновых устройств.
[wikipedia.org/wiki Лэмбовский сдвиг]. Выполненные расчеты подтверждают, что формулы (23), (25) и (26) отличаются высокой точностью и важны при расчете спиновых устройств.
Известен аналог, в котором вместо ферромагнитных металлов или сплавов используется ферромагнитный полупроводник - монооксид европия EuO. В проводящих слоях (квантовых ямах) EuO сверхрешетки EuO-SrO под действием сильного молекулярного поля, созданного обменным взаимодействием, при Т<Тс, где Тс - температура Кюри, максимальные скорости движения электронов достигают значения 3⋅107 см/с, а подвижность 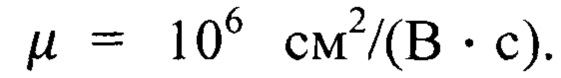 Это обеспечивает «… создание спиновых полевых транзисторов с оптимальными параметрами и наилучшими характеристиками» [Ю.Ф. Головнев, Д.А. Нургулеев, Е.В. Мараева. Спиновые транзисторы на основе гетероструктур EuO-SrO. Известия СПбГЭТУ «ЛЭТИ», №8. 2016, с. 3 - 6. С. 3, 5].
Это обеспечивает «… создание спиновых полевых транзисторов с оптимальными параметрами и наилучшими характеристиками» [Ю.Ф. Головнев, Д.А. Нургулеев, Е.В. Мараева. Спиновые транзисторы на основе гетероструктур EuO-SrO. Известия СПбГЭТУ «ЛЭТИ», №8. 2016, с. 3 - 6. С. 3, 5].
Аналог, в котором проводящим слоем (квантовой ямой) является ферромагнитный полупроводник, выбираем в качестве прототипа. Недостаток прототипа - отсутствие причинно-следственной связи состава ферромагнитного материала транзистора с дрейфовой скоростью носителей 3⋅107 см/с, подвижностью  а также с температурой Кюри ферромагнитного полупроводника. Другим недостатком прототипа является ограничение рабочих температур спинового транзистора температурой Кюри оксида европия
а также с температурой Кюри ферромагнитного полупроводника. Другим недостатком прототипа является ограничение рабочих температур спинового транзистора температурой Кюри оксида европия 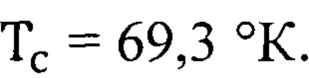
Согласно уровню науки и техники в самой простой теории электронного транспорта Друде дрейфовая скорость носителей пропорциональна электронной подвижности  и обратно пропорциональна эффективной массе
и обратно пропорциональна эффективной массе 
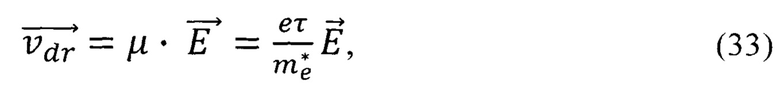
где 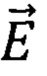 - напряженность электрического поля, в котором помещен полупроводниковый кристалл;
- напряженность электрического поля, в котором помещен полупроводниковый кристалл;
е - заряд электрона;
 - среднее время свободного пробега заряда.
- среднее время свободного пробега заряда.
В канале полевых транзисторов напряженность электрического поля Е превышает 103…104 В/см и дрейфовая скорость электронов достигает своего максимального значения  которое соответствует насыщению тока [Ю.К. Пожела, В.Г. Мокеров. Большое повышение максимальной дрейфовой скорости электронов в канале полевого гетеротранзистора. // ФТП, 2006, том 40, вып.3, с. 362].
которое соответствует насыщению тока [Ю.К. Пожела, В.Г. Мокеров. Большое повышение максимальной дрейфовой скорости электронов в канале полевого гетеротранзистора. // ФТП, 2006, том 40, вып.3, с. 362].
С учетом подвижности 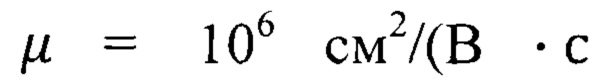 ) и напряженности электрического поля Е=3⋅104 В/см дрейфовая скорость электронов в канале гетеротранзистора теоретически достигает скорости света
) и напряженности электрического поля Е=3⋅104 В/см дрейфовая скорость электронов в канале гетеротранзистора теоретически достигает скорости света  Полагая сильное молекулярное поле в проводящих слоях (квантовых ямах) EuO прототипа Е≥3⋅104 В/см, получим, согласно известным подходам, скорости движения электронов, достигающие и даже превосходящие скорость света в вакууме. Однако в проводящих слоях EuO, как показано в прототипе, максимальные скорости движения электронов достигают значения 3⋅107 см/с, что по порядку величины соответствует максимальному значению дрейфовой скорости электронов
Полагая сильное молекулярное поле в проводящих слоях (квантовых ямах) EuO прототипа Е≥3⋅104 В/см, получим, согласно известным подходам, скорости движения электронов, достигающие и даже превосходящие скорость света в вакууме. Однако в проводящих слоях EuO, как показано в прототипе, максимальные скорости движения электронов достигают значения 3⋅107 см/с, что по порядку величины соответствует максимальному значению дрейфовой скорости электронов 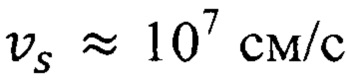 в канале полевого транзистора.
в канале полевого транзистора.
Следовательно, формула (33) не обеспечивает ограничения максимального значения дрейфовой скорости носителей.
С другой стороны в спиновом транзисторе Датта-Даса скорость носителей примерно равна 3⋅106 м/с=3⋅108 см/с, что на порядок выше скорости 3⋅107 см/с. Именно такой порядок дрейфовой скорости носителей ~ 108 см/с имеет место в гетероструктурах на квантовых точках [Ю.К. Пожела, В.Г. Мокеров. Большое повышение максимальной дрейфовой скорости электронов в канале полевого гетеротранзистора. // ФТП, 2006, том 40, вып. 3, с. 362-366; патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8].
Теоретически доказано, что для эффективного гамильтониана электронов проводимости в полупроводниковых квантовых ямах определяющими являются «…материал, кристаллографическая ориентация квантовой ямы, параметры ее потенциала и наличие внешних полей…» [М.М. Глазов. Спиновые флуктуации неравновесных электронов и экситонов в полупроводниках. // ЖЭТФ, 2016, том 149, вып.3, с. 547 - 561. С. 552].
Таким образом, установление причинно-следственной связи состава ферромагнитного материала EuO транзистора с дрейфовой скоростью носителей, а также с температурой Кюри ферромагнитного полупроводника требует вычисления неопределенности скорости обобществленных электронов в решетках кристаллов и эффективных масс носителей.

Исходные данные для европия и кислорода, а также расчеты параметров флуктуации 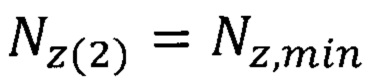 по формуле (7) и неопределенности скорости электронов
по формуле (7) и неопределенности скорости электронов 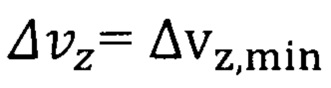 по формуле (10) представлены в табл. 5.
по формуле (10) представлены в табл. 5.
Средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла EuO 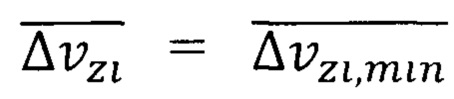 находится по упрощенной формуле
находится по упрощенной формуле
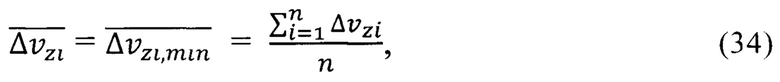
где n - количество элементов ферромагнитного материала квантовой ямы.
Подставив численные значения неопределенности скорости 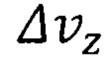 для кислорода и европия из табл. 5, получим
для кислорода и европия из табл. 5, получим  табл. 6, что примерно равно 1% от скорости света в вакууме.
табл. 6, что примерно равно 1% от скорости света в вакууме.
Для оксида европия характерна ширина запрещенной зоны Eg=1,12 эВ [wikipedia.org/wiki Оксид европия]. В связи с этим необходим расчет эффективных масс носителей для европия и кислорода. С этой целью производится расчет эффективных параметров флуктуации 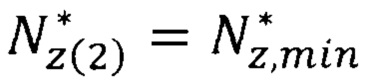 по формуле, тождественной формуле (7)
по формуле, тождественной формуле (7)

где 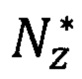 - эффективный параметр флуктуации.
- эффективный параметр флуктуации.
Эффективный параметр флуктуации обобществленного электрона атома европия в решетке кристалла EuO (квантовое состояние 8s, Eg=1,12 эВ) рассчитываем по формуле (35). Численное значение эффективного параметра флуктуации 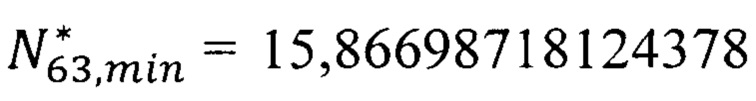 является ближайшим к параметру флуктуации электрона внешней орбиты свободного атома европия (6s, Eg=5,67 эВ)
является ближайшим к параметру флуктуации электрона внешней орбиты свободного атома европия (6s, Eg=5,67 эВ) 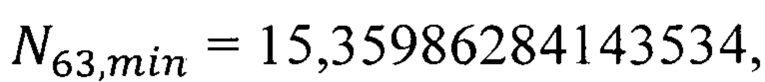 табл. 5.
табл. 5.
При этом эффективная масса носителя (дырки)  рассчитывается по формуле [см. формула (18) патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8]
рассчитывается по формуле [см. формула (18) патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8]

Подставив численные значения параметров  и
и  в формулу (36), получим
в формулу (36), получим  .
.
Эффективный параметр флуктуации обобществленного электрона атома кислорода в решетке кристалла EuO (квантовое состояние 6р, Eg=1,12 эВ) рассчитываем по формуле (35). Численное значение эффективного параметра флуктуации 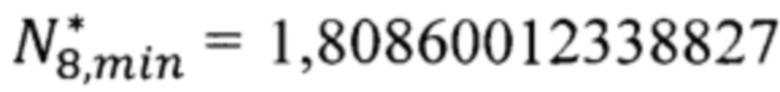 является ближайшим (по модулю) к параметру флуктуации электрона внешней орбиты свободного атома кислорода (2р, Eg=13,61 эВ)
является ближайшим (по модулю) к параметру флуктуации электрона внешней орбиты свободного атома кислорода (2р, Eg=13,61 эВ)  , табл. 5.
, табл. 5.
При этом эффективная масса носителя (электрона)  рассчитывается по формуле [см. формула (16) патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8]
рассчитывается по формуле [см. формула (16) патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8]

Подставив численные значения параметров 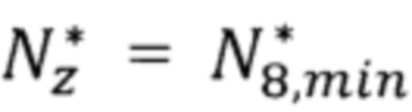 и
и  в формулу (37), получим
в формулу (37), получим 
Средняя эффективная масса носителя в решетке кристалла EuO находится по упрощенной формуле

где n - количество элементов ферромагнитного материала квантовой ямы.
Подставив численные значения параметров 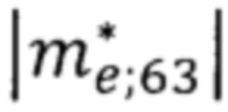 и
и 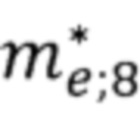 в формулу (38), получим
в формулу (38), получим 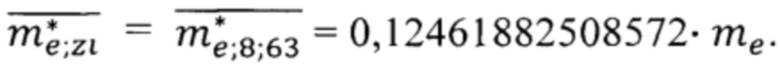
При расчете температуры Кюри ферромагнитного полупроводника используем формулу (11) с учетом средней неопределенности скорости  формула (34) и влияния эффективных масс носителей формула (38)
формула (34) и влияния эффективных масс носителей формула (38)
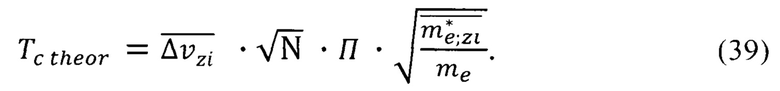
Для оксида европия молярная масса равна 167,96 г/моль, а плотность - 8,2 г/см3 [wikipedia.org/wiki Оксид европия]. На основании этих данных и с учетом числа Авогадро для оксида европия получим число N=2,94007824672541⋅1028 м-3 табл. 6.
По формуле (39) с учетом средней неопределенности скорости 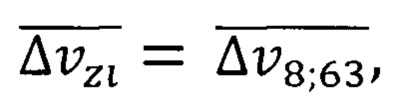 числа N и среднего значения эффективной массы носителя
числа N и среднего значения эффективной массы носителя 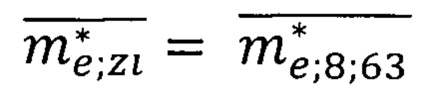 вычислим расчетное значение температуры Кюри оксида европия
вычислим расчетное значение температуры Кюри оксида европия 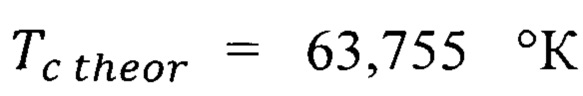 табл. 6, которое с погрешностью 8% соответствует температуре Кюри оксида европия
табл. 6, которое с погрешностью 8% соответствует температуре Кюри оксида европия 
На основании закона сохранения импульса вычисляем дрейфовую скорость носителей в канале квантовой ямы на базе оксида европия по формуле

Подставив в формулу (40) численные значения параметров 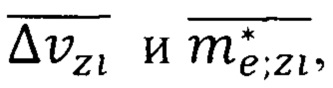 получим значение дрейфовой скорости
получим значение дрейфовой скорости  табл. 6, которое с погрешностью 5,43% соответствует дрейфовой скорости носителей
табл. 6, которое с погрешностью 5,43% соответствует дрейфовой скорости носителей 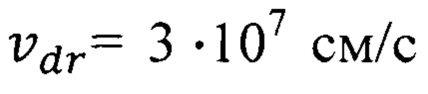 в канале оксида европия [Ю.Ф. Головнев, Д.А. Нургулеев, Е.В. Мараева. Спиновые транзисторы на основе гетероструктур EuO-SrO. Известия СПбГЭТУ «ЛЭТИ», №8. 2016, с. 3 - 6. С. 3, 5].
в канале оксида европия [Ю.Ф. Головнев, Д.А. Нургулеев, Е.В. Мараева. Спиновые транзисторы на основе гетероструктур EuO-SrO. Известия СПбГЭТУ «ЛЭТИ», №8. 2016, с. 3 - 6. С. 3, 5].

Что касается другого недостатка прототипа, а именно ограничения рабочих температур спинового транзистора температурой Кюри оксида европия  то известно о создании ферромагнитного полупроводникового композита EuO:Fe с температурой Кюри
то известно о создании ферромагнитного полупроводникового композита EuO:Fe с температурой Кюри  [О.В. Аношина, В.П. Жуков, А.С. Борухович. Электронная зонная структура и свойства твердого раствора
[О.В. Аношина, В.П. Жуков, А.С. Борухович. Электронная зонная структура и свойства твердого раствора 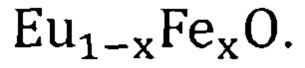 // ФТТ, 2015, т. 57, вып.11, с. 2115-2119. С. 2115]. Кроме ферромагнитных полупроводниковых композитов ожидаются более высокие температуры Кюри, например, в наноструктурах магнитных полупроводников по сравнению с их объемными образцами.
// ФТТ, 2015, т. 57, вып.11, с. 2115-2119. С. 2115]. Кроме ферромагнитных полупроводниковых композитов ожидаются более высокие температуры Кюри, например, в наноструктурах магнитных полупроводников по сравнению с их объемными образцами.
Выше показано, что в ферромагнитных материалах большую роль играет неопределенность скорости обобществленных электронов 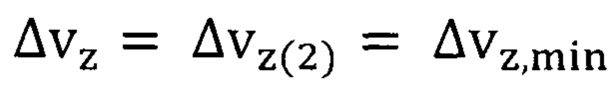 формула (10), в том числе и при нахождении постоянной молекулярного поля Вейсса по формуле (3). А в полупроводниковых гетероструктурах с составной активной областью с квантовыми точками дрейфовая скорость носителей
формула (10), в том числе и при нахождении постоянной молекулярного поля Вейсса по формуле (3). А в полупроводниковых гетероструктурах с составной активной областью с квантовыми точками дрейфовая скорость носителей 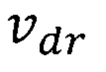 зависит от неопределенности скорости
зависит от неопределенности скорости  электронов внешних орбит атомов элементов, входящих в материал квантовой ямы [патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8]. Однако, имеет физический смысл и неопределенность скорости
электронов внешних орбит атомов элементов, входящих в материал квантовой ямы [патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8]. Однако, имеет физический смысл и неопределенность скорости 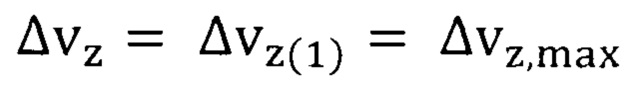 вычисляемая по формуле (9), учет которой важен при расчете спиновых устройств. Точность расчетов с использованием параметра
вычисляемая по формуле (9), учет которой важен при расчете спиновых устройств. Точность расчетов с использованием параметра  проверена при вычислении аномального магнитного момента электрона в атоме водорода по формуле (26).
проверена при вычислении аномального магнитного момента электрона в атоме водорода по формуле (26).
Для спиновых транзисторов также важным параметром является быстродействие [Ю.Ф. Головнев, Д.А. Нургулеев, Е.В. Мараева. Спиновые транзисторы на основе гетероструктур EuO-SrO. Известия СПбГЭТУ «ЛЭТИ», №8. 2016, с. 3 - 6. С. 3, 5]. В основном быстродействие зависит от дрейфовой скорости носителей.
Разработана гетероструктура с высоким числом квантовых точек, в которой максимальная дрейфовая скорость электронов значительно возрастает (примерно на порядок по сравнению с дрейфовой скоростью носителей в объемном образце аналогичного полупроводника) [В. Мокеров, Ю. Пожела, К. Пожела, В. Юцене. Гетероструктурный транзистор на квантовых точках с повышенной максимальной дрейфовой скоростью электронов. // ФТП, 2006, том 40, вып. 3, с. 367].
Известен аналог, в котором указанный выше эффект объясняется использованием такого материала квантовой ямы, состав которого и характеристики, в том числе зонная структура и эффективные массы носителей, обеспечивают повышенную квантово ограниченную дрейфовую скорость носителей 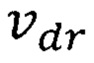 , увеличивающую быстродействие, улучшающие энергетические и частотные параметры гетеротранзистора на квантовых точках [патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8]. В аналоге дрейфовая скорость носителей
, увеличивающую быстродействие, улучшающие энергетические и частотные параметры гетеротранзистора на квантовых точках [патент на полезную модель RU 182092 U1, опубл. 03.08.2018, Бюл. №22; патент на изобретение RU 2681661 С1, опубл. 12.03.2019, Бюл. №8]. В аналоге дрейфовая скорость носителей 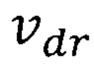 зависит от неопределенности скорости
зависит от неопределенности скорости 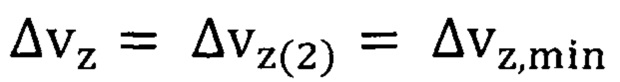 электронов внешних орбит атомов элементов, входящих в материал квантовой ямы, и вычисляется по формуле, тождественной формуле (34). Аналог включает буферный слой из широкозонного полупроводника, или полупроводника с большей шириной запрещенной зоны, чем ширина запрещенной зоны материала составной квантовой ямы. Составная активная область состоит из n - канальных слоев, в каждый из которых входит последовательно слой из материала составной квантовой ямы и слой со сформированными квантовыми точками. Ширина запрещенной зоны материала слоя квантовых точек меньше, чем материала квантовой ямы. Буферный слой может быть выполнен, например, из Si, GaN, AlAs, ZnSe, InAlAs, AlGaAs, AlSb, ZnTe, GaAsSb, AlGaSb, CdS.
электронов внешних орбит атомов элементов, входящих в материал квантовой ямы, и вычисляется по формуле, тождественной формуле (34). Аналог включает буферный слой из широкозонного полупроводника, или полупроводника с большей шириной запрещенной зоны, чем ширина запрещенной зоны материала составной квантовой ямы. Составная активная область состоит из n - канальных слоев, в каждый из которых входит последовательно слой из материала составной квантовой ямы и слой со сформированными квантовыми точками. Ширина запрещенной зоны материала слоя квантовых точек меньше, чем материала квантовой ямы. Буферный слой может быть выполнен, например, из Si, GaN, AlAs, ZnSe, InAlAs, AlGaAs, AlSb, ZnTe, GaAsSb, AlGaSb, CdS.
В спиновой электронике «… одной из трудно решаемых проблем… остается проблема осуществления устойчивого спинового переноса тока при комнатной температуре…» [ВТ. Бамбуров, А.С. Борухович, Н.И. Игнатьева. Спиновый транзистор в контакте EuO:Fe/GaAs. Доклады академии наук, 2011, том 437, №2, с. 173-177. С. 173]. А для гетероструктур на квантовых точках характерна полная температурная стабильность - независимость порового тока от температуры [Ж.И. Алферов. История и будущее полупроводниковых гетероструктур. // ФТП, 1998, том 32, №1, с. 12]. С другой стороны «… интервал энергий, в котором происходят квантовые флуктуации, не зависит от температуры. Это следует из соотношения неопределенности» [В.Ф. Гантмахер, В.Т. Долгополов. Квантовые фазовые переходы «локализованные - делокализованные электроны». // УФН, 2008, том 178, №1, с. 5].
Выполненные выше расчеты подтверждают важность учета неопределенности скорости 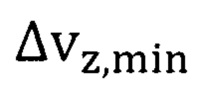 в спиновых гетероструктурах. С другой стороны в гетероструктурах на квантовых точках имеет место дрейфовая скорость носителей ~10 см/с8, что на порядок больше дрейфовой скорости, например, в спиновом транзисторе на оксиде европия. Поэтому актуальны спиновые гетероструктурные транзисторы с введенными барьерами в виде квантовых точек, например, из таких материалов, как InAs, InSb, PbSe, PbS, PbTe, SnTe в составной квантовой яме из ферромагнитного полупроводника.
в спиновых гетероструктурах. С другой стороны в гетероструктурах на квантовых точках имеет место дрейфовая скорость носителей ~10 см/с8, что на порядок больше дрейфовой скорости, например, в спиновом транзисторе на оксиде европия. Поэтому актуальны спиновые гетероструктурные транзисторы с введенными барьерами в виде квантовых точек, например, из таких материалов, как InAs, InSb, PbSe, PbS, PbTe, SnTe в составной квантовой яме из ферромагнитного полупроводника.
В связи с этим целесообразно вычисление повышенной квантово ограниченной температуры Кюри оксида европия и повышенной квантово ограниченной дрейфовой скорости носителей в соответствующем спиновом гетероструктурном транзисторе с квантовыми точками.
Рассмотрим возможность реализации повышенной минимальной квантово ограниченной температуры Кюри оксида европия, зависящей от минимальной неопределенности скорости 
В объемном образце ферромагнитного полупроводника оксида европия дрейфовая скорость носителей приближенно вычислялась по формуле (40), согласно которой дрейфовая скорость зависит от среднего значения эффективной массы носителей  элементов, входящих в состав ферромагнитного материала. Так как в полупроводниковой гетероструктуре с квантовыми точками дрейфовая скорость вычисляется по формуле, тождественной формуле (34), то есть не зависит от эффективных масс, как не зависит от эффективных масс и дрейфовая скорость носителей в ферромагнитных веществах группы железа, то и температура Кюри квантовой ямы из оксида европия со слоем квантовых точек вычисляется по формуле, тождественной формуле (11)
элементов, входящих в состав ферромагнитного материала. Так как в полупроводниковой гетероструктуре с квантовыми точками дрейфовая скорость вычисляется по формуле, тождественной формуле (34), то есть не зависит от эффективных масс, как не зависит от эффективных масс и дрейфовая скорость носителей в ферромагнитных веществах группы железа, то и температура Кюри квантовой ямы из оксида европия со слоем квантовых точек вычисляется по формуле, тождественной формуле (11)
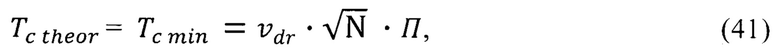
где 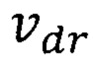 - повышенная минимальная квантово ограниченная дрейфовая скорость носителей ферромагнитного полупроводника квантовой ямы со слоем квантовых точек,
- повышенная минимальная квантово ограниченная дрейфовая скорость носителей ферромагнитного полупроводника квантовой ямы со слоем квантовых точек, 
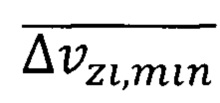 - средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла;
- средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла;
 - повышенная минимальная квантово ограниченная температура Кюри.
- повышенная минимальная квантово ограниченная температура Кюри.
В спиновой гетероструктуре с введенными барьерами в виде квантовых точек в составной квантовой яме из ферромагнитного полупроводника дрейфовая скорость вычисляется по формуле, тождественной формуле (34)

Подставив в формулу (41) численное значение параметра  а также число N из табл.6, получим для квантовой ямы из оксида европия со слоем квантовых точек повышенную минимальную квантово ограниченную температуры Кюри
а также число N из табл.6, получим для квантовой ямы из оксида европия со слоем квантовых точек повышенную минимальную квантово ограниченную температуры Кюри 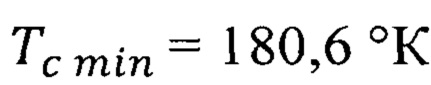 табл. 9.
табл. 9.
При расчете аномального магнитного момента электрона в атоме водорода обоснован физический смысл неопределенности скорости  вычисляемой по формуле (9), учет которой важен при разработке спиновых устройств.
вычисляемой по формуле (9), учет которой важен при разработке спиновых устройств.
Рассмотрим возможность реализации повышенной максимальной квантово ограниченной температуры Кюри оксида европия, зависящей от неопределенности скорости 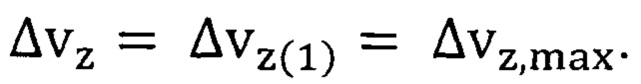
Неопределенность скорости электрона внешней орбиты свободного атома вещества  вычисляется на основании формулы (9) по известному параметру флуктуации
вычисляется на основании формулы (9) по известному параметру флуктуации  , который рассчитывается из формулы (7). Исходные данные и результаты расчета для европия и кислорода представлены в табл. 7.
, который рассчитывается из формулы (7). Исходные данные и результаты расчета для европия и кислорода представлены в табл. 7.

Среднее максимальное значение неопределенности скорости обобществленного электрона решетки кристалла оксида европия вычисляем по формуле, тождественной формуле (34)
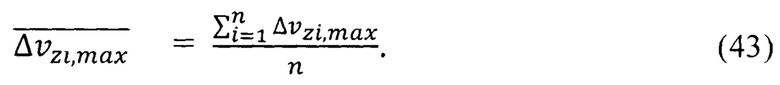
По исходным данным табл.7 на основании формулы (43) находим

Для оксида европия с шириной запрещенной зоны Eg=1,12 эВ достижение максимальных значений неопределенности скорости, указанных в табл. 7, возможно при реализации конкретных квантовых состояний, когда

Эффективный параметр флуктуации обобществленного электрона атома европия в решетке кристалла оксида европия (квантовое состояние n=9; 1=8, Eg=1,12 эВ) рассчитываем по формуле (35). Численное значение эффективного параметра флуктуации  табл. 8 является ближайшим по модулю к параметру флуктуации электрона внешней орбиты свободного атома европия (6s, Eg=5,67 эВ)
табл. 8 является ближайшим по модулю к параметру флуктуации электрона внешней орбиты свободного атома европия (6s, Eg=5,67 эВ) 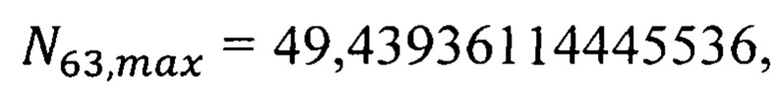 табл. 7. При этом эффективная масса носителя (электрона)
табл. 7. При этом эффективная масса носителя (электрона)  рассчитывается по формуле (37) и равна
рассчитывается по формуле (37) и равна 
Эффективный параметр флуктуации обобществленного электрона атома кислорода в решетке кристалла EuO (квантовое состояние 6s, Eg=1,12 эВ) рассчитываем по формуле (35). Численное значение эффективного параметра флуктуации  табл. 8 является ближайшим к параметру флуктуации электрона внешней орбиты свободного атома кислорода (2р, Eg=13,61 эВ)
табл. 8 является ближайшим к параметру флуктуации электрона внешней орбиты свободного атома кислорода (2р, Eg=13,61 эВ)  табл. 7. При этом эффективная масса носителя (электрона)
табл. 7. При этом эффективная масса носителя (электрона)  рассчитывается по формуле (37) и равна
рассчитывается по формуле (37) и равна 

Средняя эффективная масса носителя в решетке кристалла EuO находится по упрощенной формуле (38). Подставив численные значения параметров 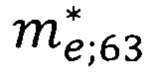 и
и 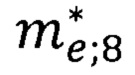 в формулу (38), получим
в формулу (38), получим  табл. 9.
табл. 9.
Повышенная максимальная квантово ограниченная температура Кюри оксида европия, зависящая от максимальных значений неопределенности скорости 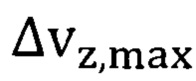 табл. 7, вычисляется по формуле, тождественной формуле (39), с учетом среднего максимального значения неопределенности скорости обобществленного электрона решетки кристалла оксида европия
табл. 7, вычисляется по формуле, тождественной формуле (39), с учетом среднего максимального значения неопределенности скорости обобществленного электрона решетки кристалла оксида европия  формула (43) и средней эффективной массы носителя в решетке кристалла EuO
формула (43) и средней эффективной массы носителя в решетке кристалла EuO  формула (38)
формула (38)
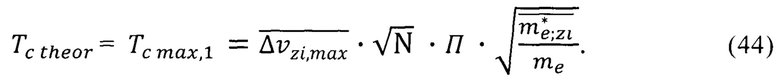
По формуле (44) с учетом параметра  числа N табл.6 и среднего значения эффективной массы носителя
числа N табл.6 и среднего значения эффективной массы носителя 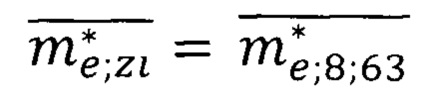 вычисляем расчетное значение повышенной максимальной квантово ограниченной температуры Кюри оксида европия
вычисляем расчетное значение повышенной максимальной квантово ограниченной температуры Кюри оксида европия 

На основании закона сохранения импульса вычисляем дрейфовую скорость носителей в канале квантовой ямы на базе оксида европия по формуле, тождественной формуле (40)

Подставив в формулу (45) численные значения параметров  и
и  получим значение дрейфовой скорости
получим значение дрейфовой скорости 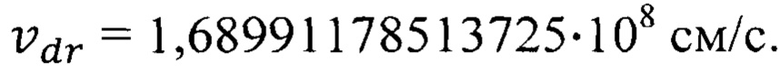
В спиновой гетероструктуре с квантовыми точками при условии  повышенная максимальная квантово ограниченная дрейфовая скорость носителей
повышенная максимальная квантово ограниченная дрейфовая скорость носителей 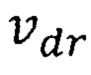 тождественна
тождественна 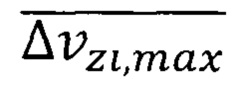 формула (43) и вычисляется по формуле (46)
формула (43) и вычисляется по формуле (46)

где 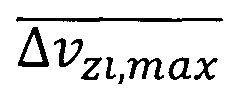 - средняя максимальная неопределенность скорости обобществленного электрона в решетке кристалла.
- средняя максимальная неопределенность скорости обобществленного электрона в решетке кристалла.
Так как в спиновой гетероструктуре с квантовыми точками дрейфовая скорость вычисляется по формуле (46), тождественной формуле (34), то есть не зависит от эффективных масс, как не зависит от эффективных масс и дрейфовая скорость носителей в ферромагнитных веществах группы железа, то и температура Кюри квантовой ямы из оксида европия со слоем квантовых точек вычисляется по формуле, тождественной формуле (11)

где 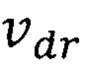 - повышенная максимальная квантово ограниченная дрейфовая скорость носителей ферромагнитного полупроводника квантовой ямы со слоем квантовых точек,
- повышенная максимальная квантово ограниченная дрейфовая скорость носителей ферромагнитного полупроводника квантовой ямы со слоем квантовых точек, 
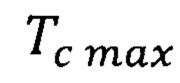 - повышенная максимальная квантово ограниченная температура Кюри.
- повышенная максимальная квантово ограниченная температура Кюри.
Подставив в формулу (47) численное значение параметра 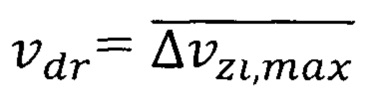 , а также число N из табл.6, получим для квантовой ямы из оксида европия со слоем квантовых точек повышенную максимальную квантово ограниченную температуры Кюри
, а также число N из табл.6, получим для квантовой ямы из оксида европия со слоем квантовых точек повышенную максимальную квантово ограниченную температуры Кюри 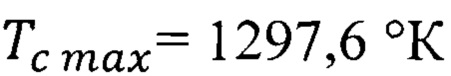 табл. 9.
табл. 9.
С учетом магнитного момента электрона формула (26) для больших дрейфовых скоростей носителей формулу (47) следует записать в виде

В этом случае для квантовой ямы из оксида европия со слоем квантовых точек получим уточненное значение повышенной максимальной квантово ограниченной температуры Кюри 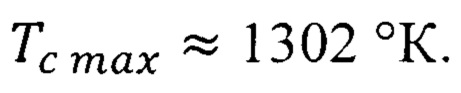
Очевидно, что ферромагнитный полупроводниковый композит EuO:Fe с температурой Кюри 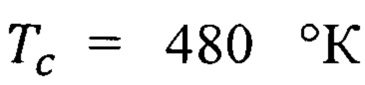 [О.В. Аношина, В.П. Жуков, А.С. Борухович. Электронная зонная структура и свойства твердого раствора Eu1-xFexO. // ФТТ, 2015, т.57, вып.11, с. 2115 - 2119. С.2115] обеспечивает более высокую температуру Кюри, чем Tcmin=180,6°К для спиновой гетероструктуры с составной квантовой ямой из оксида европия с квантовыми точками из полупроводникового материала и зависящей от минимальных значений неопределенности скорости
[О.В. Аношина, В.П. Жуков, А.С. Борухович. Электронная зонная структура и свойства твердого раствора Eu1-xFexO. // ФТТ, 2015, т.57, вып.11, с. 2115 - 2119. С.2115] обеспечивает более высокую температуру Кюри, чем Tcmin=180,6°К для спиновой гетероструктуры с составной квантовой ямой из оксида европия с квантовыми точками из полупроводникового материала и зависящей от минимальных значений неопределенности скорости 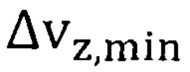 , и даже чем
, и даже чем  зависящей от максимальных значений неопределенности скорости
зависящей от максимальных значений неопределенности скорости 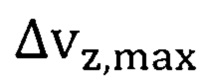 и средней эффективной массы носителя в решетке кристалла EuO. Это означает, что в композите EuO:Fe атомы железа обеспечивают реализацию конкретных квантовых состояний для атомов европия и кислорода, когда эффективные параметры флуктуации электронов внешних орбит этих атомов
и средней эффективной массы носителя в решетке кристалла EuO. Это означает, что в композите EuO:Fe атомы железа обеспечивают реализацию конкретных квантовых состояний для атомов европия и кислорода, когда эффективные параметры флуктуации электронов внешних орбит этих атомов 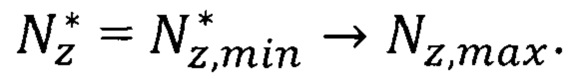
На основании изложенного выше можно заключить, что условием реализации для квантовой ямы из оксида европия или иных ферромагнитных полупроводников, например, EuS, CdCr2Se4, CdCr2S4, HgCr2Se4, CuCr2Se3Br2, GaMnAs, со слоем квантовых точек, повышенной максимальной квантово ограниченной температуры Кюри является использование в качестве слоя квантовых точек конкретного ферромагнитного материала из группы железа: Fe, Со, Ni, Gd, Dy, Tb, Ho, Er, Tm.
Таким образом, установлена причинно-следственная связь состава ферромагнитного материала со скоростью дрейфа носителей, а также с температурой Кюри ферромагнетика.
Установлена физическая сущность постоянной молекулярного поля Вейсса λ, зависящей от неопределенности скорости электрона на внешней орбите атома ферромагнитного вещества группы железа с порядковым номером Z Периодической системы элементов формула (3), или от неопределенности скоростей электронов на внешних орбитах атомов элементов, входящих в состав ферромагнитного полупроводника.
Установлена физическая сущность спина электрона, инвариантного новым преобразованиям (22), иллюстрирующим переходы вращающихся систем отсчета.
Обоснована повышенная квантово ограниченная дрейфовая скорость носителей  , которая в частном случае равна
, которая в частном случае равна 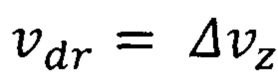 , где
, где - минимальная неопределенность скорости электрона на внешней орбите атома ферромагнитного вещества группы железа с порядковым номером Z Периодической системы элементов формула (10). А для ферромагнитного полупроводника
- минимальная неопределенность скорости электрона на внешней орбите атома ферромагнитного вещества группы железа с порядковым номером Z Периодической системы элементов формула (10). А для ферромагнитного полупроводника  зависит от средней неопределенности скорости обобществленного электрона и средней эффективной массы носителя в решетке кристалла формулы (40), (45). В спиновой гетероструктуре с введенными барьерами в виде квантовых точек в составной квантовой яме из ферромагнитного полупроводника дрейфовая скорость равна средней неопределенности скорости обобществленного электрона в решетке кристалла
зависит от средней неопределенности скорости обобществленного электрона и средней эффективной массы носителя в решетке кристалла формулы (40), (45). В спиновой гетероструктуре с введенными барьерами в виде квантовых точек в составной квантовой яме из ферромагнитного полупроводника дрейфовая скорость равна средней неопределенности скорости обобществленного электрона в решетке кристалла  формула (42) в случае слоя квантовых точек, выполненных из полупроводниковых материалов, и ограничивается сверху
формула (42) в случае слоя квантовых точек, выполненных из полупроводниковых материалов, и ограничивается сверху  формула (46) в случае слоя квантовых точек, выполненных из ферромагнитных металлов группы железа. При расчетах применяются неопределенности скорости
формула (46) в случае слоя квантовых точек, выполненных из ферромагнитных металлов группы железа. При расчетах применяются неопределенности скорости  формулы (9), (10). Поэтому различается повышенная минимальная квантово ограниченная дрейфовая скорость
формулы (9), (10). Поэтому различается повышенная минимальная квантово ограниченная дрейфовая скорость  и повышенная максимальная квантово ограниченная дрейфовая скорость
и повышенная максимальная квантово ограниченная дрейфовая скорость 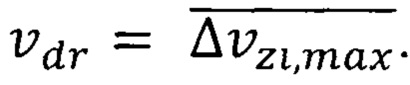
Обоснованная повышенная минимальная квантово ограниченная температура Кюри 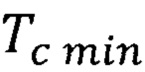 формула (41) и повышенная максимальная квантово ограниченная температура Кюри
формула (41) и повышенная максимальная квантово ограниченная температура Кюри 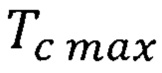 формулы (47) и (48) характерны для любого ферромагнитного полупроводникового материала квантовой ямы, например, EuO, EuS, CdCr2Se4, CdCr2S4, HgCr2Se4, CuCr2Se3Br2, GaMnAs в составе спиновой гетероструктуры с квантовыми точками.
формулы (47) и (48) характерны для любого ферромагнитного полупроводникового материала квантовой ямы, например, EuO, EuS, CdCr2Se4, CdCr2S4, HgCr2Se4, CuCr2Se3Br2, GaMnAs в составе спиновой гетероструктуры с квантовыми точками.
В результате выполненных расчетов доказана возможность улучшения энергетических параметров, частотных характеристик и быстродействия спиновых гетеротранзисторов на квантовых точках, обеспечения устойчивого спинового переноса тока й увеличения диапазона рабочих температур спиновых устройств.
Технической задачей заявленного изобретения является разработка спиновой гетероструктуры с составной активной областью с квантовыми точками, включающей такой ферромагнитный полупроводниковый материал составной квантовой ямы, который обеспечивает повышенную квантово ограниченную дрейфовую скорость носителей vdr, позволяющую значительно увеличить быстродействие, улучшить технические характеристики, такие, как энергетические параметры и частотные свойства, а также обеспечивает возможность реализации повышенной квантово ограниченной температуры Кюри ферромагнитного полупроводника квантовой ямы, что в совокупности с влиянием слоя квантовых точек, выполненных из полупроводниковых материалов или ферромагнитных металлов группы железа, способствует устойчивому спиновому переносу тока и увеличению диапазона рабочих температур устройства.
Реализация указанной технической задачи заявленным изобретением обеспечивает следующий технический результат, являющийся суммой полученных технических эффектов:
- используется ферромагнитный полупроводниковый материал составной квантовой ямы спиновой гетероструктуры с квантовыми точками, состав которого и характеристики, в том числе зонная структура и эффективные массы носителей, обеспечивают повышенную квантово ограниченную дрейфовую скорость носителей  , увеличивающую быстродействие спинового гетеротранзистора на квантовых точках, улучшающие энергетические параметры и частотные свойства;
, увеличивающую быстродействие спинового гетеротранзистора на квантовых точках, улучшающие энергетические параметры и частотные свойства;
- причинно-следственная связь ферромагнитного полупроводникового материала составной квантовой ямы спиновой гетероструктуры с квантовыми точками и его характеристик со скоростью дрейфа носителей в канале спинового гетеротранзистора на квантовых точках определяет квантовое ограничение на минимальное и максимальное значение повышенной дрейфовой скорости носителей в зависимости от материала квантовых точек;
- причинно-следственная связь ферромагнитного полупроводникового материала составной квантовой ямы спиновой гетероструктуры с квантовыми точками и его характеристик с температурой Кюри ферромагнитного полупроводника квантовой ямы определяет квантовое ограничение на минимальное и максимальное значение повышенной температуры Кюри ферромагнитного полупроводникового материала составной квантовой ямы в зависимости от материала квантовых точек;
- причинно-следственная связь ферромагнитного полупроводникового материала составной квантовой ямы спиновой гетероструктуры с квантовыми точками и его характеристик, в том числе зонной структуры, с повышенной квантово ограниченной скоростью дрейфа носителей и повышенной температурой Кюри ферромагнитного полупроводникового материала определяет температуру Кюри в пределах минимального и максимального значения 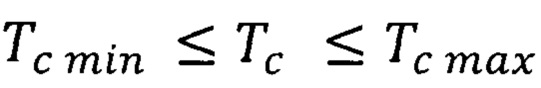 ;
;
- повышенная квантово ограниченная скорость дрейфа носителей и повышенная квантово ограниченная температура Кюри ферромагнитного полупроводникового материала квантовой ямы обеспечивают устойчивый спиновый перенос тока и увеличение диапазона рабочих температур спинового устройства;
- конструктивная особенность спиновой гетероструктуры с составной активной областью с квантовыми точками состоит в использовании п>1 барьеров в виде квантовых точек, введенных в составную квантовую яму, что образует п>1 канальных слоев, в каждый из которых последовательно входит слой из ферромагнитного полупроводникового материала, формирующего квантовую яму и слой квантовых точек, выполненных из полупроводниковых материалов или ферромагнитных металлов группы железа, обеспечивающих повышенную квантово ограниченную скорость дрейфа носителей и повышенную квантово ограниченную температуру Кюри ферромагнитного полупроводникового материала квантовой ямы, а также дополнительное повышение выходной мощности за счет увеличения числа канальных слоев, которые, как и максимальное число п, ограничиваются тепловым режимом работы прибора и/или техническим заданием на выходную мощность.
Для достижения указанного технического результата предложена «Спиновая гетероструктура с составной активной областью с квантовыми точками», содержащая последовательно конкретный ферромагнитный полупроводниковый материал из состава, например, EuO, EuS, CdCr2Se4, CdCr2S4, HgCr2Se4, CuCr2Se3Br2, GaMnAs, формирующий квантовую яму и введенные барьеры в виде квантовых точек из конкретного полупроводникового материала, например, InAs, InSb, PbSe, PbS, PbTe, SnTe или конкретного ферромагнитного металла группы железа, например, Fe, Со, Ni, Gd, Dy, Tb, Ho, Er, Tm в составной квантовой яме.
Принципиальным отличием предлагаемой спиновой гетероструктуры с составной активной областью с квантовыми точками от прототипа является то, что используется составная активная область, в которую входит слой из ферромагнитного полупроводникового материала, формирующего квантовую яму и слой квантовых точек, обеспечивающих повышенную квантово ограниченную скорость дрейфа носителей и повышенную квантово ограниченную температуру Кюри ферромагнитного полупроводникового материала квантовой ямы, при этом повышенная минимальная квантово ограниченная скорость дрейфа носителей  вычисляется по упрощенной формуле (42)
вычисляется по упрощенной формуле (42)

где 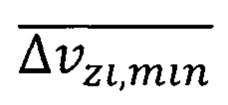 - средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла, формула (34);
- средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла, формула (34);
n - количество элементов материала квантовой ямы;
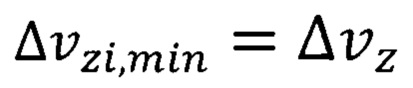 - минимальная неопределенность скорости движения электронов в центральном поле на внешней орбите свободного атома / - го элемента, входящего в состав ферромагнитного полупроводникового материала квантовой ямы, а движение электронов соответствует уравнению движения электрона в радиальных волновых функциях формула (5)
- минимальная неопределенность скорости движения электронов в центральном поле на внешней орбите свободного атома / - го элемента, входящего в состав ферромагнитного полупроводникового материала квантовой ямы, а движение электронов соответствует уравнению движения электрона в радиальных волновых функциях формула (5)

где 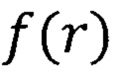 - радиальная волновая функция;
- радиальная волновая функция;
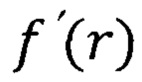 - первая производная радиальной волновой функции;
- первая производная радиальной волновой функции;
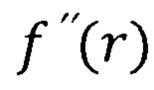 - вторая производная радиальной волновой функции;
- вторая производная радиальной волновой функции;
 - постоянная Планка;
- постоянная Планка;
me - масса элементарного заряда;
Е - собственное значение энергии электрона;
е - заряд электрона;
V(r) - заданная функция, зависящая только от радиуса и определяющая потенциал поля, 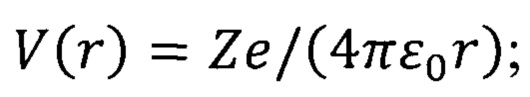
r - радиус траектории движения заряда;
Z - атомный номер;
 - диэлектрическая постоянная;
- диэлектрическая постоянная;
N - некоторое действительное число, решение которого дает собственные значения энергии электрона (6)

где n - главное квантовое число;
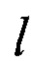 - орбитальное квантовое число;
- орбитальное квантовое число;
Nz - параметр флуктуации,
а одно из решений приравнивается потенциалу ионизации Ez атома элемента Периодической системы (7)
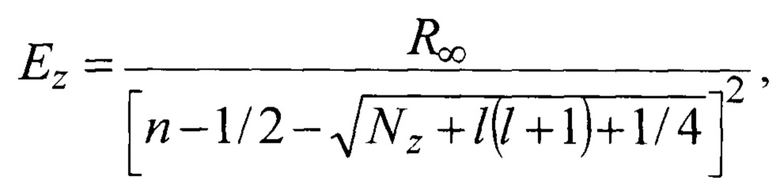
где  - постоянная Ридберга,
- постоянная Ридберга, 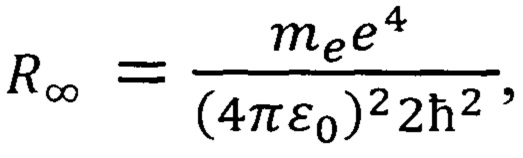
для нахождения параметра флуктуации Nz и соответствующей неопределенности скорости движения электронов на внешней орбите свободных атомов элементов, причем результатом решения являются два значения параметра флуктуации 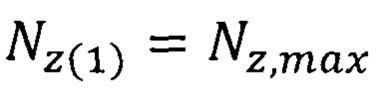 и
и 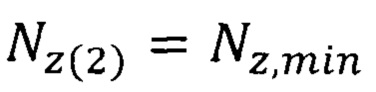 , то есть
, то есть  а для нахождения
а для нахождения 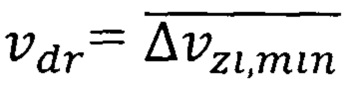 по формуле (42) используется минимальная неопределенность скорости (10)
по формуле (42) используется минимальная неопределенность скорости (10)

где rz - радиус атома с атомным номером Z,
при этом повышенная квантово ограниченная температура Кюри ферромагнитного полупроводника квантовой ямы ограничивается снизу повышенной минимальной квантово ограниченной температурой Кюри 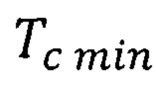 формула (41)
формула (41)
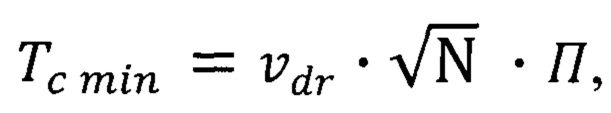
где 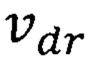 - повышенная минимальная квантово ограниченная дрейфовая скорость носителей формула (42),
- повышенная минимальная квантово ограниченная дрейфовая скорость носителей формула (42), 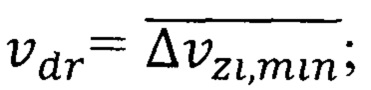
 - средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла, формула (34);
- средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла, формула (34);
N - число, зависящее от плотности и атомной массы вещества, N=плотность ⋅ N/атомная масса;
NA - число Авогадро;
П - некоторая постоянная, 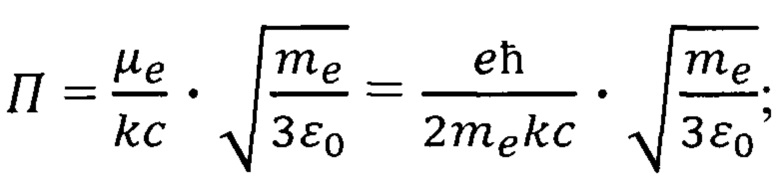
 - спиновый магнитный момент электрона,
- спиновый магнитный момент электрона, 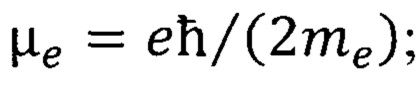
е - электрический заряд электрона;
 - постоянная Планка;
- постоянная Планка;
ε0 - электрическая постоянная;
с - скорость света в вакууме, а дрейфовая скорость носителей  определяет постоянную молекулярного поля Вейсса λ формула (3)
определяет постоянную молекулярного поля Вейсса λ формула (3)

где  - тепловая скорость электронов ферромагнитного материала,
- тепловая скорость электронов ферромагнитного материала, 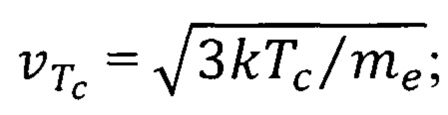 k - постоянная Больцмана;
k - постоянная Больцмана;
Тс - температуры Кюри, 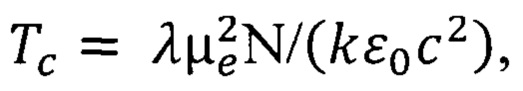 а сверху повышенная квантово ограниченная температура Кюри ферромагнитного полупроводника квантовой ямы ограничивается повышенной максимальной квантово ограниченной температурой Кюри
а сверху повышенная квантово ограниченная температура Кюри ферромагнитного полупроводника квантовой ямы ограничивается повышенной максимальной квантово ограниченной температурой Кюри 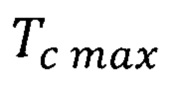 формула (47)
формула (47)
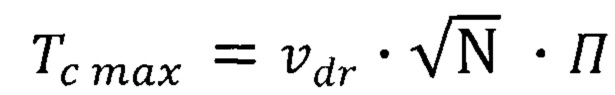
где 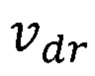 - повышенная максимальная квантово ограниченная дрейфовая скорость носителей формула (46)
- повышенная максимальная квантово ограниченная дрейфовая скорость носителей формула (46)
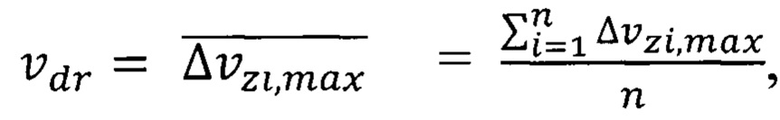
где 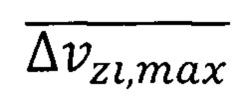 - средняя максимальная неопределенность скорости обобществленного электрона в решетке кристалла, формула (43), а для нахождения параметра
- средняя максимальная неопределенность скорости обобществленного электрона в решетке кристалла, формула (43), а для нахождения параметра 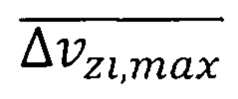 используется максимальная неопределенность скорости (9)
используется максимальная неопределенность скорости (9)

а в случае больших значений дрейфовой скорости носителей  необходимо учитывать магнитный момент электрона по релятивистской формуле (26) и повышенную максимальную квантово ограниченную температуру Кюри
необходимо учитывать магнитный момент электрона по релятивистской формуле (26) и повышенную максимальную квантово ограниченную температуру Кюри  формула (47) следует вычислять по релятивистской формуле (48)
формула (47) следует вычислять по релятивистской формуле (48)

где множитель вида 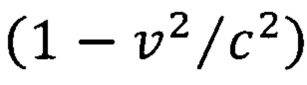 относится к преобразованиям Лоренца, а множитель вида
относится к преобразованиям Лоренца, а множитель вида 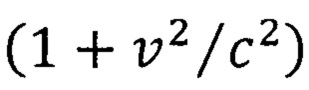 относится к новым преобразованиям формула (22), иллюстрирующим переходы вращающихся систем отсчета
относится к новым преобразованиям формула (22), иллюстрирующим переходы вращающихся систем отсчета

где х, y,z, t - координаты событий в системе отсчета К;
х', y', z', t' - координаты тех же событий в системе отсчета К'.
Дополнительными отличиями является то, что конструктивная особенность спиновой гетероструктуры с составной активной областью с квантовыми точками состоит в использовании n≥1 барьеров в виде квантовых точек, введенных в составную квантовую яму, что образует n≥1 канальных слоев, в каждый из которых последовательно входит слой из ферромагнитного полупроводникового материала, формирующего квантовую яму и слой квантовых точек, выполненных из полупроводниковых материалов или ферромагнитных металлов группы железа, обеспечивающих повышенную квантово ограниченную скорость дрейфа носителей и повышенную квантово ограниченную температуру Кюри ферромагнитного полупроводникового материала квантовой ямы, а также дополнительное повышение выходной мощности за счет увеличения числа канальных слоев, которые, как и максимальное число n, ограничиваются тепловым режимом работы прибора и/или техническим заданием на выходную мощность.
Другими дополнительными отличиями является то, что спиновая гетероструктура с составной активной областью с квантовыми точками включает последовательно буферный слой из широкозонного полупроводника, или полупроводника с большей шириной запрещенной зоны, чем ширина запрещенной зоны следующего далее ферромагнитного полупроводникового материала составной квантовой ямы, из состава, например, Si, GaN, AlAs, ZnSe, InAlAs, AlGaAs, AlSb, ZnTe, GaAsSb, AlGaSb, CdS, а ширина запрещенной зоны полупроводникового материала из состава, например, InAs, InSb, PbSe, PbS, PbTe, SnTe, следующего далее слоя квантовых точек меньше, чем ширина запрещенной зоны ферромагнитного полупроводникового материала квантовой ямы из состава, например, EuO, EuS, CdCr2Se4, CdCr2S4, HgCr2Se4, CuCr2Se3Br2, GaMnAs, причем слой квантовых точек может быть выполнен из конкретного ферромагнитного металла из состава группы железа: Fe, Со, Ni, Gd, Dy, Tb, Ho, Er, Tm. Кроме того в спиновых гетероструктурах с составной активной областью с квантовыми точками могут быть реализованы различные способы управления спиновым током.
Именно наличие в заявленном изобретении общих отличительных и дополнительных отличительных признаков позволяет изготавливать СВЧ спиновые гетеротранзисторы на квантовых точках, монолитные интегральные схемы, а также элементы спиновой памяти и логики с различными способами управления спиновым током, с улучшенными энергетическими параметрами, частотными характеристиками и быстродействием, устойчивым спиновым переносом тока и увеличенным диапазоном рабочих температур.
Составная активная область состоит из n≥1 канальных слоев, в каждый из которых последовательно входит слой из ферромагнитного полупроводникового материала, формирующего квантовую яму и слой квантовых точек, выполненных из полупроводниковых материалов или ферромагнитных металлов группы железа. Толщина слоя из ферромагнитного полупроводникового материала составной квантовой ямы и толщина слоя со сформированными квантовыми точками в пределах единиц нанометров для каждого слоя. Концентрация квантовых точек большая, выше 3⋅1010 см-2. Суммарная толщина составной активной области с квантовыми точками зависит от числа n≥1 канальных слоев, обеспечивающих реализацию повышенной квантово ограниченной дрейфовой скорости носителей, повышенной квантово ограниченной температуры Кюри ферромагнитного полупроводникового материала составной квантовой ямы и дополнительное повышение выходной мощности за счет увеличения числа канальных слоев, которое, как и максимальное значение n, ограничивается тепловым режимом работы прибора или техническим заданием на выходную мощность.
Установленная причинно-следственная связь ферромагнитного полупроводникового материала составной квантовой ямы спиновой гетероструктуры с квантовыми точками и его характеристик со скоростью дрейфа носителей в канале спинового гетеротранзистора на квантовых точках определяет квантовое ограничение на минимальное и максимальное значение повышенной дрейфовой скорости носителей.
Установленная причинно-следственная связь ферромагнитного полупроводникового материала составной квантовой ямы спиновой гетероструктуры с квантовыми точками и его характеристик, в том числе зонной структуры, с повышенной квантово ограниченной скоростью дрейфа носителей и повышенной квантово ограниченной температурой Кюри ферромагнитного полупроводникового материала определяет повышенную температуру Кюри Тс в пределах минимального и максимального значения  .
.
Условием реализации повышенной квантово ограниченной дрейфовой скорости носителей является исключение рассеяния на оптических фононах, снижающего величину дрейфовой скорости, а также исключение влияния эффективных масс носителей ферромагнитного полупроводникового материала составной квантовой ямы на величину дрейфовой скорости. Для этого вводятся в составную квантовую яму барьеры в виде квантовых точек, выполненные из полупроводниковых материалов или ферромагнитных металлов группы железа.
Условием реализации повышенной минимальной квантово ограниченной температура Кюри ферромагнитного полупроводника квантовой ямы является установленная причинно-следственная связь температуры Кюри  формула (41) и повышенной минимальной квантово ограниченной скорости дрейфа носителей
формула (41) и повышенной минимальной квантово ограниченной скорости дрейфа носителей 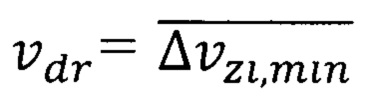 формула (42) за счет введения в составную квантовую яму барьеров в виде квантовых точек, выполненные из полупроводниковых материалов.
формула (42) за счет введения в составную квантовую яму барьеров в виде квантовых точек, выполненные из полупроводниковых материалов.
Условием реализации повышенной максимальной квантово ограниченной температура Кюри ферромагнитного полупроводника квантовой ямы является установленная причинно-следственная связь температуры Кюри 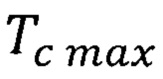 формулы (47), (48) и повышенной максимальной квантово ограниченной скорости дрейфа носителей
формулы (47), (48) и повышенной максимальной квантово ограниченной скорости дрейфа носителей 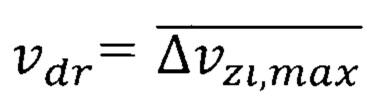 формула (46) за счет введения в составную квантовую яму барьеров в виде квантовых точек, выполненные из ферромагнитных металлов группы железа.
формула (46) за счет введения в составную квантовую яму барьеров в виде квантовых точек, выполненные из ферромагнитных металлов группы железа.
Заявленное изобретение «Спиновая гетероструктура с составной активной областью с квантовыми точками» является новым, не использованным в науке и технике до даты приоритета заявленного изобретения, устройством для изготовления СВЧ спиновых гетеротранзисторов на квантовых точках, монолитных интегральных схем, а также элементов спиновой памяти и логики с различными способами управления спиновым током, с улучшенными энергетическими параметрами, частотными характеристиками и быстродействием, устойчивым спиновым переносом тока и увеличенным диапазоном рабочих температур. Заявленное изобретение обладает следующими достоинствами:
- используется ферромагнитный полупроводниковый материал составной квантовой ямы спиновой гетероструктуры с квантовыми точками, состав которого и характеристики, в том числе зонная структура и эффективные массы носителей, обеспечивают повышенную квантово ограниченную дрейфовую скорость носителей  , увеличивающую быстродействие спинового гетеротранзистора на квантовых точках, улучшающие энергетические параметры и частотные свойства;
, увеличивающую быстродействие спинового гетеротранзистора на квантовых точках, улучшающие энергетические параметры и частотные свойства;
- причинно-следственная связь ферромагнитного полупроводникового материала составной квантовой ямы спиновой гетероструктуры с квантовыми точками и его характеристик со скоростью дрейфа носителей в канале спинового гетеротранзистора на квантовых точках определяет квантовое ограничение на минимальное и максимальное значение повышенной дрейфовой скорости носителей в зависимости от материала квантовых точек;
- причинно-следственная связь ферромагнитного полупроводникового материала составной квантовой ямы спиновой гетероструктуры с квантовыми точками и его характеристик с температурой Кюри ферромагнитного полупроводника квантовой ямы определяет квантовое ограничение на минимальное и максимальное значение повышенной температуры Кюри ферромагнитного полупроводникового материала составной квантовой ямы в зависимости от материала квантовых точек;
- причинно-следственная связь ферромагнитного полупроводникового материала составной квантовой ямы спиновой гетероструктуры с квантовыми точками и его характеристик, в том числе зонной структуры, с повышенной квантово ограниченной скоростью дрейфа носителей и повышенной температурой Кюри ферромагнитного полупроводникового материала определяет температуру Кюри в пределах минимального и максимального значения 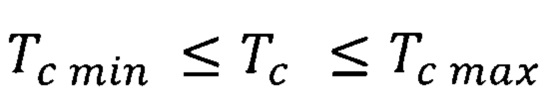 ;
;
- повышенная квантово ограниченная скорость дрейфа носителей и повышенная квантово ограниченная температура Кюри ферромагнитного полупроводникового материала квантовой ямы обеспечивают устойчивый спиновый перенос тока и увеличение диапазона рабочих температур спинового устройства;
- конструктивная особенность спиновой гетероструктуры с составной активной областью с квантовыми точками состоит в использовании n≥1 барьеров в виде квантовых точек, введенных в квантовую яму, что образует n≥1 канальных слоев.
Заявленное изобретение промышленно применимо, так как для его реализации используются широко известные материалы и технологии производства СВЧ спиновых и полупроводниковых гетероструктур гетеротранзисторов, монолитных интегральных схем, а также элементы спиновой памяти и логики.
| название | год | авторы | номер документа |
|---|---|---|---|
| Гетероструктура с составной активной областью с квантовыми точками | 2018 |
|
RU2681661C1 |
| СПИНОВЫЙ ТРАНЗИСТОР | 2008 |
|
RU2387047C1 |
| Способ формирования тонкой пленки монооксида европия на кремниевой подложке с получением эпитаксиальной гетероструктуры EuO/Si | 2020 |
|
RU2739459C1 |
| СВЕТОИЗЛУЧАЮЩИЙ ДИОД | 2009 |
|
RU2400866C1 |
| СПОСОБ ФОРМИРОВАНИЯ ЭПИТАКСИАЛЬНЫХ ГЕТЕРОСТРУКТУР EuO/Ge | 2021 |
|
RU2768948C1 |
| СПИНТРОННЫЙ КОМПОЗИЦИОННЫЙ МАТЕРИАЛ | 2004 |
|
RU2291134C2 |
| СПОСОБ ПОЛУЧЕНИЯ ТОНКОПЛЕНОЧНОГО ОКСИДНОГО МАТЕРИАЛА, ЛЕГИРОВАННОГО ИОНАМИ ФЕРРОМАГНИТНОГО МЕТАЛЛА, ДЛЯ СПИНТРОНИКИ | 2007 |
|
RU2360317C2 |
| СПОСОБ УМЕНЬШЕНИЯ НАМАГНИЧЕННОСТИ МАГНИТНЫХ ОКСИДНЫХ МАТЕРИАЛОВ | 1992 |
|
RU2077618C1 |
| СПОСОБ ЗАЩИТЫ ОТ ПОДДЕЛОК И КОНТРОЛЯ ПОДЛИННОСТИ ЦЕННЫХ ИЗДЕЛИЙ НА ОСНОВЕ ЦИРКУЛЯРНОГО ФОТОГАЛЬВАНИЧЕСКОГО ЭФФЕКТА В ПОЛУПРОВОДНИКОВЫХ НАНОСТРУКТУРАХ | 2007 |
|
RU2356093C1 |
| МАГНИТОРЕЗИСТИВНЫЙ СПИНОВЫЙ СВЕТОДИОД | 2020 |
|
RU2748909C1 |
Использование: для изготовления СВЧ гетеротранзисторов на квантовых точках. Сущность изобретения заключается в том, что спиновая гетероструктура с составной активной областью с квантовыми точками содержит введенные барьеры в виде квантовых точек в квантовой яме, при этом используется составная активная область, в которую последовательно входит слой из ферромагнитного полупроводникового материала, формирующего квантовую яму и слой квантовых точек, состав которой и характеристики обеспечивают повышенную квантово-ограниченную скорость дрейфа носителей и повышенную квантово-ограниченную температуру Кюри ферромагнитного полупроводникового материала квантовой ямы. Технический результат: обеспечение возможности увеличения быстродействия, улучшения энергетических параметров и частотных характеристик, устойчивого спинового переноса тока и увеличения диапазона рабочих температур спиновых устройств. 6 з.п. ф-лы.
1. Спиновая гетероструктура с составной активной областью с квантовыми точками, содержащая квантовую яму из ферромагнитного полупроводника, отличающаяся тем, что используется составная активная область, в которую последовательно входит слой из ферромагнитного полупроводникового материала, формирующего квантовую яму, и слой квантовых точек, обеспечивающая повышенную квантово-ограниченную скорость дрейфа носителей и повышенную квантово-ограниченную температуру Кюри ферромагнитного полупроводникового материала квантовой ямы, при этом повышенная минимальная квантово-ограниченная скорость дрейфа носителей  вычисляется по упрощенной формуле
вычисляется по упрощенной формуле

где 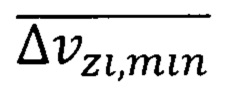 - средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла;
- средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла;
n - количество элементов материала квантовой ямы;
 - минимальная неопределенность скорости движения электронов в центральном поле на внешней орбите свободного атома i-го элемента, входящего в состав ферромагнитного полупроводникового материала квантовой ямы, а движение электронов соответствует уравнению движения электрона в радиальных волновых функциях
- минимальная неопределенность скорости движения электронов в центральном поле на внешней орбите свободного атома i-го элемента, входящего в состав ферромагнитного полупроводникового материала квантовой ямы, а движение электронов соответствует уравнению движения электрона в радиальных волновых функциях
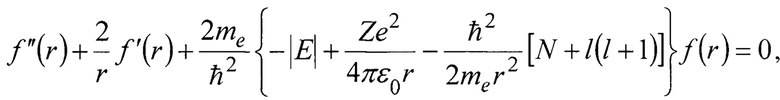
где  - радиальная волновая функция;
- радиальная волновая функция;
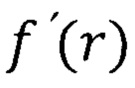 - первая производная радиальной волновой функции;
- первая производная радиальной волновой функции;
 - вторая производная радиальной волновой функции;
- вторая производная радиальной волновой функции;
 - постоянная Планка;
- постоянная Планка;
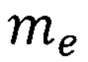 - масса элементарного заряда;
- масса элементарного заряда;
Е - собственное значение энергии электрона;
е - заряд электрона;
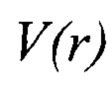 - заданная функция, зависящая только от радиуса и определяющая потенциал поля,
- заданная функция, зависящая только от радиуса и определяющая потенциал поля, 
r - радиус траектории движения заряда;
Z - атомный номер;
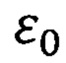 - диэлектрическая постоянная;
- диэлектрическая постоянная;
N - некоторое действительное число, решение которого дает собственные значения энергии электрона
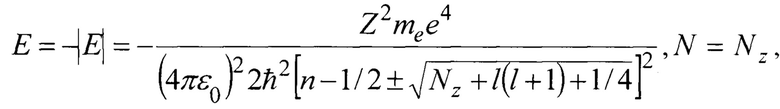
где n - главное квантовое число;
 - орбитальное квантовое число;
- орбитальное квантовое число;
Nz - параметр флуктуации, а одно из решений приравнивается потенциалу ионизации Ez атома элемента Периодической системы

где  - постоянная Ридберга,
- постоянная Ридберга, 
для нахождения параметра флуктуации Nz и соответствующей неопределенности скорости движения электронов на внешней орбите свободных атомов элементов, причем результатом решения являются два значения параметра флуктуации  и
и 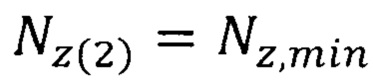 , то есть
, то есть  , а для нахождения скорости дрейфа
, а для нахождения скорости дрейфа 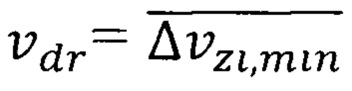 используется минимальная неопределенность скорости
используется минимальная неопределенность скорости

где rz - радиус атома с атомным номером Z,
при этом повышенная квантово-ограниченная температура Кюри ферромагнитного полупроводника квантовой ямы ограничивается снизу повышенной минимальной квантово-ограниченной температурой Кюри
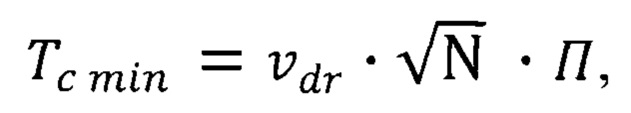
где 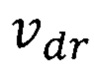 - повышенная минимальная квантово-ограниченная дрейфовая скорость носителей,
- повышенная минимальная квантово-ограниченная дрейфовая скорость носителей, 
 - средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла;
- средняя минимальная неопределенность скорости обобществленного электрона в решетке кристалла;
N - число, зависящее от плотности и атомной массы вещества, N = плотность ⋅ N/атомная масса;
NA - число Авогадро;
П - некоторая постоянная, 
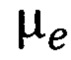 - спиновый магнитный момент электрона,
- спиновый магнитный момент электрона, 
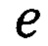 - электрический заряд электрона;
- электрический заряд электрона;
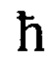 - постоянная Планка;
- постоянная Планка;
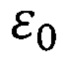 - электрическая постоянная;
- электрическая постоянная;
с - скорость света в вакууме;
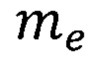 - масса элементарного заряда;
- масса элементарного заряда;
k - постоянная Больцмана, а дрейфовая скорость носителей  определяет постоянную молекулярного поля Вейсса
определяет постоянную молекулярного поля Вейсса 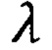
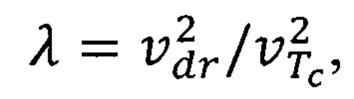
где  - тепловая скорость электронов ферромагнитного материала,
- тепловая скорость электронов ферромагнитного материала,
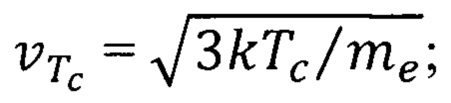
Тс - температуры Кюри, 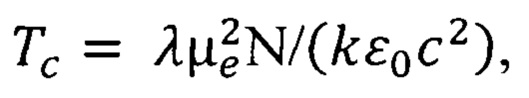
а сверху повышенная квантово-ограниченная температура Кюри ферромагнитного полупроводника квантовой ямы ограничивается повышенной максимальной квантово-ограниченной температурой Кюри
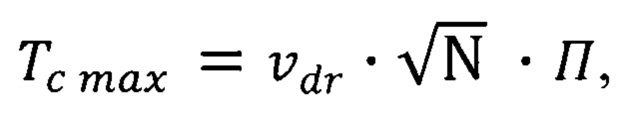
где 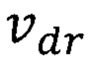 - повышенная максимальная квантово-ограниченная дрейфовая скорость носителей
- повышенная максимальная квантово-ограниченная дрейфовая скорость носителей

где 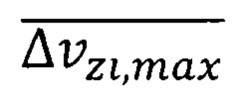 - средняя максимальная неопределенность скорости обобществленного электрона в решетке кристалла, а для нахождения параметра
- средняя максимальная неопределенность скорости обобществленного электрона в решетке кристалла, а для нахождения параметра  используется максимальная неопределенность скорости
используется максимальная неопределенность скорости
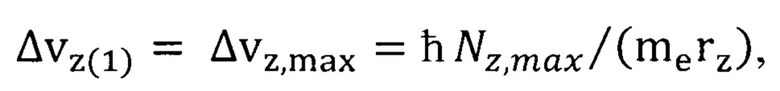
а в случае больших значений дрейфовой скорости носителей 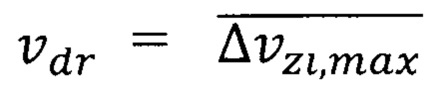 необходимо учитывать магнитный момент электрона, рассчитанный по релятивистской формуле, и повышенную максимальную квантово-ограниченную температуру Кюри
необходимо учитывать магнитный момент электрона, рассчитанный по релятивистской формуле, и повышенную максимальную квантово-ограниченную температуру Кюри 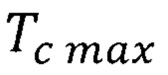 следует вычислять по релятивистской формуле
следует вычислять по релятивистской формуле

где множитель вида  относится к преобразованиям Лоренца, а множитель вида
относится к преобразованиям Лоренца, а множитель вида 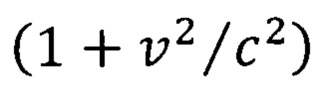 относится к новым преобразованиям, иллюстрирующим переходы вращающихся систем отсчета
относится к новым преобразованиям, иллюстрирующим переходы вращающихся систем отсчета

где х, y, z, t - координаты событий в системе отсчета К;
х', у', z', t' - координаты тех же событий в системе отсчета К'.
2. Устройство по п. 1, отличающееся тем, что спиновая гетероструктура с составной активной областью с квантовыми точками включает буферный слой из широкозонного полупроводника или полупроводника с большей шириной запрещенной зоны, чем ширина запрещенной зоны материала составной квантовой ямы, который может быть выполнен, например, из состава таких материалов, как Si, GaN, AlAs, ZnSe, InAlAs, AlGaAs, AlSb, ZnTe, GaAsSb, AlGaSb, CdS.
3. Устройство по пп. 1, 2, отличающееся тем, что спиновая гетероструктура с составной активной областью с квантовыми точками включает слой из ферромагнитного полупроводникового материала, формирующего квантовую яму, который может быть выполнен, например, из состава таких материалов, как EuO, EuS, CdCr2Se4, CdCr2S4, HgCr2Se4, CuCr2Se3Br2, GaMnAs.
4. Устройство по пп. 1-3, отличающееся тем, что слой квантовых точек может быть выполнен, например, из таких полупроводниковых материалов, как InAs, InSb, PbSe, PbS, PbTe, SnTe.
5. Устройство по пп. 1-3, отличающееся тем, что слой квантовых точек может быть выполнен, например, из таких ферромагнитных металлов группы железа, как Fe, Со, Ni, Gd, Dy, Tb, Ho, Er, Tm.
6. Устройство по пп. 1-5, отличающееся тем, что конструктивная особенность спиновой гетероструктуры с составной активной областью с квантовыми точками состоит в использовании n≥1 барьеров в виде квантовых точек, введенных в составную квантовую яму, что образует n≥1 канальных слоев.
7. Устройство по пп. 1-6, отличающееся тем, что в спиновых гетероструктурах с составной активной областью с квантовыми точками могут быть реализованы различные способы управления спиновым током.
| Спин-детектор свободных электронов на основе полупроводниковых гетероструктур | 2016 |
|
RU2625538C1 |
| ФЕРРОМАГНИТНАЯ ПОЛУПРОВОДНИКОВАЯ ГЕТЕРОСТРУКТУРА | 2009 |
|
RU2425184C1 |
| CN 106449734 A, 22.02.2017 | |||
| US 7309887 B2, 18.12.2007. | |||
Авторы
Даты
2024-07-10—Публикация
2023-07-26—Подача