тике и вычислительной технике и может быть использовано в автоматизированных системах проектирования для преобразования представления логических функций из-совершенной дизъюн ктивной Нормальной формы в полиноминальную и наоборот. Известен метод tJ преобразования совершенной дизъюнктивной нормальной формы (СДНФ) в полиноминальную форму, который заключается в том, что коэффициенты полино- . ма Жегалкина функции f ч, 0 « х. ,.,. . . , +),...,Хг,могут быть вычислены че3 таблицу истинности функции f (х) (или СДНФ) путем умножения на матрицу S и суммирования произведений . по модулю 2: o«i.-Vi t - ° ° ...,f(l,..,-l)5 5s-P Л п-1 ,5 io О J Устройство, реализующеетакой метод, характеризуется большой аппарат ной сложностью. Наиболее близким к предлагаемому является преобразователь формы представления логических функций, содержащий счетчик, коммутатор, шифратор счетные триггеры, элементы И и НЕ, имеющие 2 входов и 2 выходов, где П-- количество переменных логической функции, которое предназначено для преобразования логических функций из совершенной дизъюктивной нормальной формы в полиноминальнуюС2 Этот преобразователь имеет низкое быстродействие, поскольку резуль тат формируется за 2 тактов. ,т Целью изобретения является повышение быстродействия, Поставленная цель достигается тем что преобразователь формы представления логических функций, имеющий г,п о / 2 входов и 2 выходов (п- количество логических переменных), содержит п ярусов элементов неравнозначности по 2 элементов неравнозначности в каждом, при этом в каждом К-м ярусе (,..,,п) элементы нерав oh-k .нозначности образуют 2 групп по 2.,элементов неравнозначности в f.ajicMtsHiue nc xtenuanctHnui Tn о каждо й, входы i-го элемента неравно() м и (21)-м входами преобразователя (i 1, . . ., ), выходы элементов неравнозначности (2 1-1)-й и / 21Ьй групп Р-го яруса (6 1,..., Рг,..., n-IJ соединены со входами соответствующих элементов неравнозначности 1-й группы (Р+Г)-го яруса, выходы элементов неравнозначности S (2я-1)-й и (8-2я)-й ГРУПП q,1,..., t V..,n-2) t-го яруса соединены со входами ментов неравнозначности с ( по ( ) -и q-й группы ( яруса, входы ( 2 )-го элемент элемента неравнозначности Ь-и группы d-ro яруса (,... . -, ,...nj соединены с 2(2V1)-M и 2 2h-M входами преобразователя, выходы элементов неравнозначности последней группы каждого яруса и вход преобразователя являются выходами преобразователя. На чертеже приведена функциональная схема преобразователя формы представления логических функций дпя случая . Преобразователь содержит входы Ц - Ig , выходы 2 - 2g, элементы неравнозначности 3 - 3 первого яруса, элементы неравнозначности 1 второго яруса, элементы неравнозначности 5 - 54 третьего яруса. Преобразователь работает следующим образом, Любая логическая функция от п переменных может быть представлена в полиноминальной форме. /, г P() ,п./, 2-sx,x,(i) „„ , Особенностью этой формы представле.„ ния является TOi что переменная X.. - п входит только в конъюнк.ции с номерами ()-( ) т.а, во вторую половину полинома. Поэтому полином , „ / ч функции F (х) может быть представ лен в виде Р(Х)/ ® I - 1 V-rj© 5)Х,ГЛ .(+ (,--,i) |--, ,п-1., 2 z +i -i - /. . f / i ii « n-t/ n i(i r -i/ 311 т.е. полином функции F (х; от п пере менных представляет собой сумму по модулю 2 полинома функции п- переменной .и умноженного на х полинома, функции f от п-1 переменной, причем порядок следования коньюн1 ций переменных в этих двух полиномах одинаков. Из формулы (1)-при х„ О имеем с1х -F/X Olf fx Х Vl- -i / 1 1- -откуда ,1х,..-х.,)Р(х,,...,х„.,0| а при имеем X.r{.-,V-t.(.-,Xn-i)® Э(.-.-,), откудаf2(.-iVll flK-V.l)®(l--Vl) ,...,X,Oj0F(x,...,x,1). Пусть полином функции Р(х,,.,,л„.,0 имеет вид ,. .),..., х„, , а полином функции F(x,..,,Xp.,,1j - вид Р(х„...,х„ „1}М ©Л.х ®, 0А . XT п-т ; 011.- -1 X X 1 п-1 Тогда согласно формуле (1) полином функции F (х) может быть получеи следующим образом F(X)f,(x,,...,Vi)(N.-.Vi) («„..,Vll)(N-Vl.4® ,,©.-.eV.; .-iP-nlKe /ie-OA,, v.....,©;., ,x.,....,0л ч 2 -1 , р./ .-v, . . 1 v o oJn®( 1®%) iXn®--j(3( n-i )i2 --in 2-1/ . ,...,®/1,.,х.,...,х„.© Г)В X к « fTi (Ф|й 1г o nU,.,X2.-,. аким образом, преобразование функции .F (х) из СДНФ в полиноминальную форму может быть получено,если предварительно преобразованы из 14 СДНФ в полиноминальную форму ее подфункции f(n,-;,,0} и Р(х,...,х, 1/ Обозначим сигналы на входах I преобразователя через б,,,..., выходах 2 преобразователя через ir;,-сг, , ..., t о Для преобразования формы представления логической функции от переменных из СДНФ в полиноминальную на вхоДЬ1 преобразователя подается таблица истинности функции F(xl--P( х„...,д„) в порядке возрастания наборов, причем х считается младшим разрядом, а X f, - старшим. Таким образом, имеем (0.0.....0,0) , (1.0,...,0,0),... ,.-, .) , 6 ., Р(0,0,...,ОЛ), 2i ,..,(1,1,...,1.1) . Поскольку переменная х„ старшая, то для всей первой половинй таблицы истинности х„ о, а для всей второй х„ 1. Поэтому первая половина таблицы истинности фунющи F{x,,... ) представляет собой таблицу истинности ее подфункции F(x,,..,x.,o) , вторая половина таблицы истинности функции F(x,..., х„) представляет собой таблицу истинности ее подфункции F( х,,..., х,,, 1J . Предположим, что осуществляется преобразование СДНФ функций Р(х,„.,Хр ,0} и Г(х,,..„х„.„1). Тогда на выходах 2 преобразователл имеем ,..,,,.,,„.., , ,;, м,. ,, „.,и..л; 6Г .,.,..;..,,. .,. Следовательно, преобразователь формирует на своих выходах коэффициенты полинома Жегалкина функции F (к), т.е. преобразует СДНФ функции-F (х) в ее полиномииальную форму. В случае использования преобразователя на п переменных для вычисления коэффициентов полинома функц,„ j, j( переменных, , таблица истинности этой функции подается на первые 2 входов преобразователя, а результат считывается с его первых 2 выходов:. 5112428 Преобразование формы представле,НИЯ логических функций из ПОЛИНОМИнальной в СДНФ. Подадим на йхбдь преобразователя формы представления логических функ-5 ,ций от j переменш х коэффициенты полинома функции , X ot. oL )C 0с Х®...®С- 1 j j-f-f n/ о « С X° (, /-N г 4 ii i®j( cF(x,...,Xj,0 , ,...,.jF|x,...,Xj, 0,oL.. ,..,dJlS)Hy,.-,i.,-4n) ij-l n / VT IT 1T7 ill 1 /V, J JJ . J J Гл 1 j4.i ®20 1 .-С , . 2 2.25 . . . ,р, Р/ . л «/ / i V 1 y+f nj |-130 А з -i-f V Р/л А л о iJ, eJL ff} N k/ TiP2r./ yH j i-%) г , . I 0Р(/Ь1.А2..,.0..-. 1 (F{lb,,,,...,jb..,1,d-,...,d)((b,ft.,... V 1 J 1 JT1 /J -.,/ j i( . . , 2 -1, - выходах преобразователя от j переменных формируется таблица истинности функции F(x,,...,x,.,Dt.j,,...,ctJ , etjv,...,oine{o,1 , причем переменная ней считается старшей среди переменных х - Хг. В случае использования преобразователя на п переменных для преобразования формы ..представления функ °i; К переменных, , на перr К TiLiiQ 9 «Tf/Snno гтпопЛпагаоиятогта ттпття вые 2 ВХОДОВ преобразователя подаются коэффициенты Ад - А. полинома функции, а коэффициенты СДНФ формируются на первых 2 выходах преобразователя. Таким образом, преобразователь является устройством комбинационного типа, что выгодно отличает его от прототипа по быстродействию, устройство построено на одном типе логических элементов и имеет регулярную структуру, что повышает технологичность его конструкции; кроме того, данное устройство позволяет осуществлять не только прямое преобразование, но и обратное без изменения своей структуры, что, расширяет его функциональные возМОЖНОСТИ.
12.
2i


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для полиномиального разложения логических функций | 1987 |
|
SU1441380A1 |
| Преобразователь формы представления логических функций | 1987 |
|
SU1474671A1 |
| Преобразователь формы представления логических функций | 1983 |
|
SU1164728A1 |
| Преобразователь формы представления логических функций | 1987 |
|
SU1441381A1 |
| Преобразователь формы представления логических функций | 1984 |
|
SU1242984A1 |
| Преобразователь формы представления логических функций | 1987 |
|
SU1441379A2 |
| Устройство для преобразования булевых функций | 1988 |
|
SU1532946A1 |
| Функциональный преобразователь | 1983 |
|
SU1140130A1 |
| Устройство для вычисления булевых производных | 1988 |
|
SU1534456A2 |
| Функциональный преобразователь | 1986 |
|
SU1388890A1 |
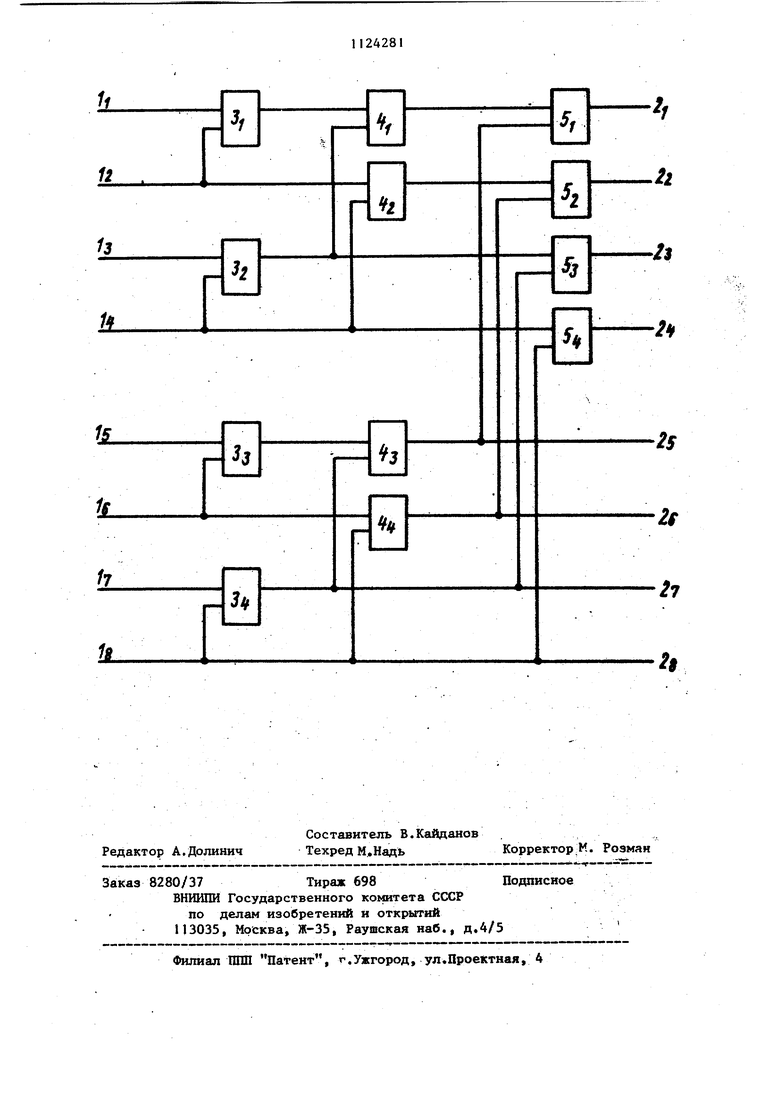
ПРЕОБРАЗОВАТЕЛЬ ФОРМЫ ПРЕДСТАВЛЕНИЯ ЛОГИЧЕСКИХ ФУНКЦИЙ, имею-щий 2 входов и 2 выходов (п- количество логических переменных), о т личающийся тем, что, с целью повьшения быстродействия, преобразователь содержит о. ярусов элементов неравнозначности по 2 элемеиjTOB неравнозначности в каждом, при .этом в каждом R-M ярусе (,,..,h) элементы наравнозначности обрузуют групп по 2 элементов неравнозначности в каждой) входы i-ro элемента неравнозначности первого яруса соединены с 
/J
и
Is
h
1s
3if
18
-/I
3
Л
Ф
-25
2f
27
29
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Авсаркисян Г.С | |||
| и др | |||
| Представление логических функций в виде полиномов Л{егалкина | |||
| Автоматика и вычислительная техника, 1975, № 6, с.6-10 | |||
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Авторское сви,цетельство СССР № 781822, кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| . | |||
Авторы
Даты
1984-11-15—Публикация
1983-01-28—Подача