.Изобретение относится к цифровой вычислительной технике и может быть использовано для аппаратной поддержки вычислений в комплексах автоматизированного проектирования дискретных устройств, обработки изображений, сжатия данных, в системах синтеза топологии БИС и СБИС, фильтров на поверхностных акустических волнах.
Цель изобретения - расширение класса решаемых задач за счет реализации преобразования булевых функций ъ арифметическую полиноминальную форму Хаара.
В основу изобретения положены следующие математические модели компонентов устройств и их взаимодействия в процессе функционирования. ta«.,) -j
Спектр Хаара Hf h(0)... h i булевой функции п переменных f(x(,..., х„) f(x) определяется в виде
Н - if Х,
где Xf х
(о)
„се1
«(1)
) - вектор
Нгп
размерности 2 , элементами которого являются значения булевой, функции f (х) на упорядоченных в лексикографическом порядке наборах переменных (значения таблицы истинности)j матрица преобразования Хаара, формируемая по рекуррентному соотношению
ел
со ьэ
со
Јь Од
. Н« .
Ht;C-il
где k 2,п;
(2)
- символ кронекеровского произведения:
- символ транспонирования; - единичная матрица порядка
2 Л- I
Используя свойства преобразования Хаара, можно показать, что спектр Хаара Н булевой функцией f(x) записывается в аналитической форме следующим образом:







| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для распознавания на линейность булевых функций | 1988 |
|
SU1552169A1 |
| Устройство для преобразования по функциям Хаара | 1986 |
|
SU1327119A1 |
| Устройство для вычисления булевых производных | 1987 |
|
SU1481793A1 |
| Устройство для вычисления импликант | 1989 |
|
SU1686460A1 |
| Статистический анализатор | 1985 |
|
SU1280395A1 |
| Устройство для вычисления булевых производных | 1988 |
|
SU1518825A2 |
| Устройство для решения булевых дифференциальных уравнений | 1989 |
|
SU1661791A1 |
| Устройство для распознавания на линейность булевых функций | 1990 |
|
SU1756879A1 |
| Устройство для вычисления булевых производных | 1986 |
|
SU1370651A1 |
| Магнитооптическое устройство для реализации дискретного преобразования Фурье | 1990 |
|
SU1795472A1 |
Изобретение относится к цифровой вычислительной технике и может быть использовано для аппаратной поддержки вычислений в комплексах автоматизированного проектирования дискретных устройств, обработки изображений, сжатия данных, в системах синтеза топологии БИС и СБИС, фильтров на поверхностных акустических волнах. Цель изобретения - расширение класса решаемых задач за счет реализации преобразования булевых функций в арифметическую полиномиальную форму Хаара. Поставленная цель достигается за счет того, что в состав устройства введены коммутатор, блок нормировки, блок синхронизации и N-1 блоков конъюнктивного преобразования (N - число переменных функции). 2 з.п. ф-лы, 11 ил., 4 табл.
Ht(x) (h 01
X, (Л Г ХЛ, t (il, -,-Ј+V- -,1n-zt2 1
+(-D V +...-н2г(-1) 21 ь Ы x,
1-2.
1
CX I
I J
где if - r-й разряд двоичного представления параметра i (нумерация разрядов начиная со старших, т.е. слева напра во)}
,n-1 -параметр, соответствующий
номеру группы строк матрицы Хаара (фиг.1);
X е(0,0 -j-я булева переменная булевой функции f(x). Особенностью выражения (3) является то, что Hf(x) е(0,0 на любых наборах логических переменных (xv, х, ..., хп). Причем на одинаковых наборах значения Н(х) и Х совпадают. Это означает, что выражение (3) является арифметико-логическим представлением булевой функции f(x), поскольку в нем содержатся арифметические и логические операции. Другой важной особенностью выражения (3) является его взаимооднозначная связь с булевой функцией f(х). Другими ело- вами, любую булеву функцию f(x) можно единственным образом представить в виде (3), а по выражению (3) можно однозначно восстановить булеву функцию f (х).
Рассмотрим пример. Пусть булева функция f(x4,xe) задана своим вектором значений Х#, т.е. таблицей истинН ности на наборах xf
оно .
Определим ее спектр
Н{ - Ј Н,г- Х4 - J
Запишем форму Хаара Н.(х) булевой функции согласно (3)
Н|(х) i 2Н)4 (-Х ч- х,)1
8 табл. 2 представлены спектры Хаара Hf некоторых булевых функций
z+i
(3)
1-2.
5
0
5
i,
J-f
35
0
40
- 1
О,
f(x), заданных в табл. 1 своими векторами значений Xj.
Выражение (3) есть интерпретация спектра Хаара булевой функцией,причем такая интерпретация, что булева функция f(x) представлена в новой арифметико-логической форме. В схемо-техни- ческом плане это реализуется посредством известных устройств, выполняющих дискретное преобразование Хаара или быстрое дискретное преобразование Хаара с последующей интерпретацией результата (спектра) согласно выражению (3).
Новая арифметико-логическая форма булевых функций (3) обладает рядом достоинств арифметического и логического свойств спектра Хаара, обеспечивающих выявление поведения функции на отдельных или группах наборов, однако имеет и недостатки. Основной из них связан с неполиномиальным представлением, что существенно при анализе и синтезе, например, линейных форм булевых функций.
Полиномиальную форму Хаара Pllf(x) булевой функции f(х) определим в виде:
PHj(x) . -Усь1 1 +
у, -h
in
h-
Уц п-ЛХ4 4 Xh-«
(V
где у} А,(х,)
(-О ,
aY + а1
««;
А«.- .4) -а™ + а(я . хй.4 +
)
...+ап -х, хй. „ ,хп.( .
Как видно из (k) полиномиальная форма Хаара Р1Ц(х) булевой функции .
f(x) представляет собой взвешенную сумму спектральных коэффициентов Хаа- ра и h° и арифметических полиномов А-, (х, .. ,х ,) (i 1 ,n-l). Определим функцию нормировки
S3(hC°):, 9 -l,hci)0,
(5)
Sq ht0Ho,
1, h(0, / 2,, Эта запись означает, что каждому спектральному коэффициенту Хаара h(lj , представленному m-разрядным числом со знаком, ставится в соответствие двухразрядное число со знаком Sg (htn) , формируемое по правилу (5). Таким образом, спектральные коэффициенты Хаара h( номируются по признаку знака, т.е. приводятся к величине Sf(h(n), принимающей только три значения
И ° 11Тогда с учетом нормировки в матричной записи связь коэффициентов полиномов А(х (), ..., А„. (х,xh, )
со спектральными коэффициентами Хаа- ра булевой функции определяется через конъюнктивное преобразование
А, Ka,-ss(h Mt5);
(6)
Afl-«
где
А,
Kjn-i за
ютт.
t J
S«,h
(«к-О
АИ-
Гаю) a
(. П-4 л п-
«.--IjT
a rx-t
5,(Ь Н Ъ ))-S,(hl )V .
S9(h(H-tb ts9(h(..S()T.PH|I(X) ш . 2,). . Н)Ч +
+ (-1)Э (1 - Хй- х.,Ха) + (-1)«{1 - - ха - хйхл - xt + 2х,х3 - Х4х5х3)3;
Кйр - матрица конъюнктивного пре- 45 образования, определяемая рекуррентным соотношением:
KQ.®Kup- ; K , J,
р - 2,п-1.(7)
С учетом.принятых обозначений математическая модель предлагаемого устройства (k) принимает вид:
pH|(x)
hle + ... ., х
, 89( )| .
|5
Поясним математическую модель (о) на конкретном примере.
Пусть задана булевая функция Ј(х) своим вектором значений Х 10011110 .
В результате преобразования Хаара вектора Х| получают вектор коэффициентов спектра Хаара Н/
Н,
- 1 2 - 2 О .
Находят полиномиальную форму Хаара (РН-форму) этой булевой функции.
Записывают векторы Sq(h) и Sq(h):
)
О 1 1 -1
Г; ,т
О 1 ,
Sa- (h ЙЛ
s9(ht)
и выполняют конъюнктивное преобразо- ние каждого из них
А,
1
-2 -1
3
Следовательно, в полиномиальную форму Хаара РН(х) булевой функции f(x) входят полиномы
А«(х
Az(x, ,х) М - 2ха - х( + Зх, ха и ее окончательный вид согласно (8):
PHf(x) У + 24угх +
+ 22у,,О - 2xi - х4 + Зх(х4).
Для булевых функций f(x), залгнных своими векторами значений Хг4 Г10000110П100011 Т , Х|г 0000111011101101 т , Хь 010001110111000f}T .
РН-форма имеет вид
PH|I(X) ш . 2,). . Н)Ч +
(-1)Э (1 - Хй- х.,Ха) + (-1)«{1 - ха - хйхл - xt + 2х,х3 - Х4х5х3)3;
(х) - 3(-0Х +(-1)« +
РН
ft1
50
55
+ (-1) (х, + х, - х,х.) + (-I) х х (хгхэ + х,хэ - х,Х2Х5);
PH(jc) -,(-l)xt + (-1)Хэх
х (1 - 2x4 - 2x, - 2x«xa) + {-1)M -1 + x3 - 2x4 + 2x5X3 + x,xe -2x,xax3) .
Те же функции в форме полинома Же- галкина имеют вид
Ff( (х) 1®хч©х9© XjX4© X2 хь€ х,®
© хлх ©х,х2хйф х тлгхэ; Ft,(x) - XQ© X4x3x4©x © ,х2х,хА;
Fb(x) х4ф XjX4© .
10
/ Результатом реализации математической модели (8) является арифметическая полиномиальная форма Хаара PHj(x) булевой функции f(x), характерная
-однозначным описанием исходной булевой функции,
-арифметическими операциями типа сложения и вычитания над ее членами (умножение на переменную yj . (-1) есть операция модуляции знака, так как у1 Ј а умножение на константы вида 2 реализуется посредством сдвигов),
-композицией полиномов от булевых 20 переменных, которые определяются через знаки коэффициентов Хаара.
Последнее обстоятельство является определяющим в пользу полиномиальной
15
юнктивного преобразования и синхронизации.
Блок 2 нормировки обеспеч преобразование спектральных циентов Хаара h(1) (j 2,2nответствии с математической (5) его функционирования, т разует m-разрядный спектрал фициент Хаара h в двухразр значение функции нормировки в соответствии с табл. 3.
Блок 2 нормировки содержи гистров 5 и п-1 элементов ИЛ
Первый блок 3 конъюнктив разования содержит i вычисли узлов, каждый из которых со вычитателя 7, коммутатора 8 ра 9, и счетчик 10.
Рассмотрим работу п-1 бл
формы Хаара булевой функции, посколь- 25 юнктивного преобразования 3
ре 1-го блока конъюнктивног зования 3 () (табл. М рительно счетчик 10 установ тояние 00. Введем обозначен
ку позволяет описать и численно определить локальные свойства булевой функции с помощью полиномиальных моделей : упрощает описание и вычисление булевых функций линейных по Хаару, что представляет новый класс булевых функций, имеющих удобное в представлении и реализации линейное описание (линейных в особом смысле), расширяна примере 1-го блока конъюнктивного преобразования 3 () (табл. М. Предварительно счетчик 10 установлен в состояние 00. Введем обозначение xi
30 S«(h°) (j 2Т«-1).J
Первым рабочим тактом блока 3 конъюнктивного преобразования является пятый такт работы устройства (табл. t), На пятом такте значение
ющий множество булевых функций, пред- 35 элемента Sij(h) поступает на инфор- -- мационный вход первого вычислитель40
ставимых в том или ином смысле линейными формами, обеспечивает на этой основе представление систем булевых функций.
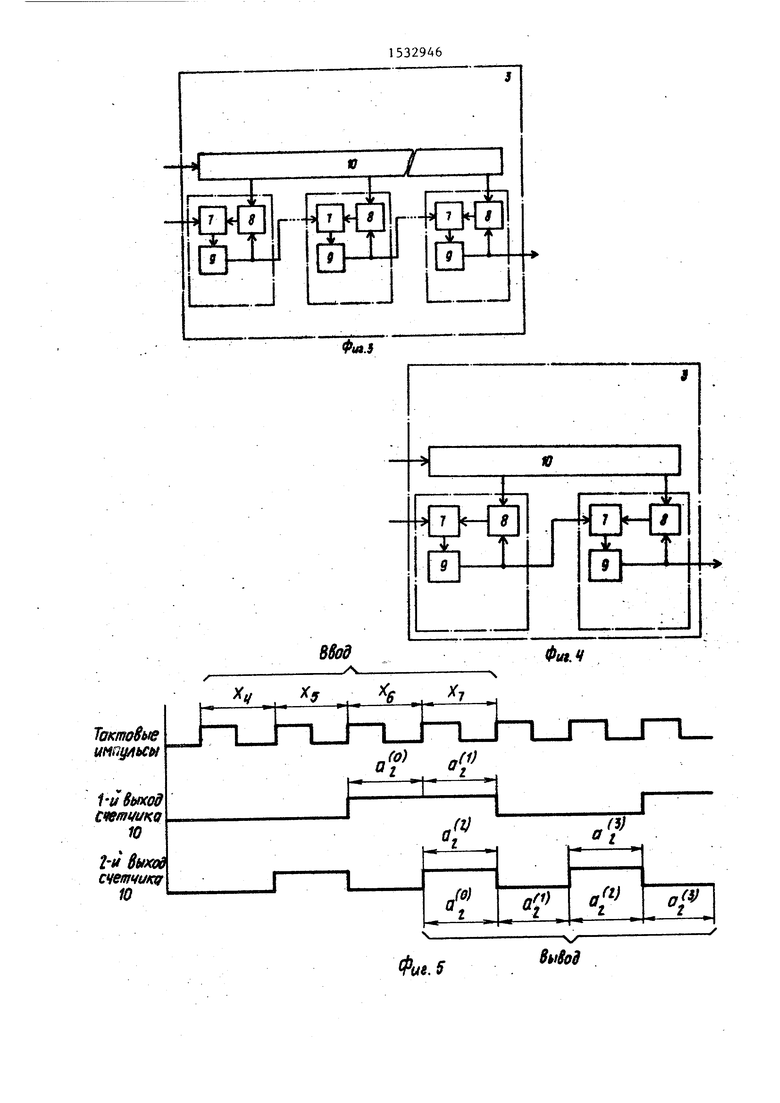
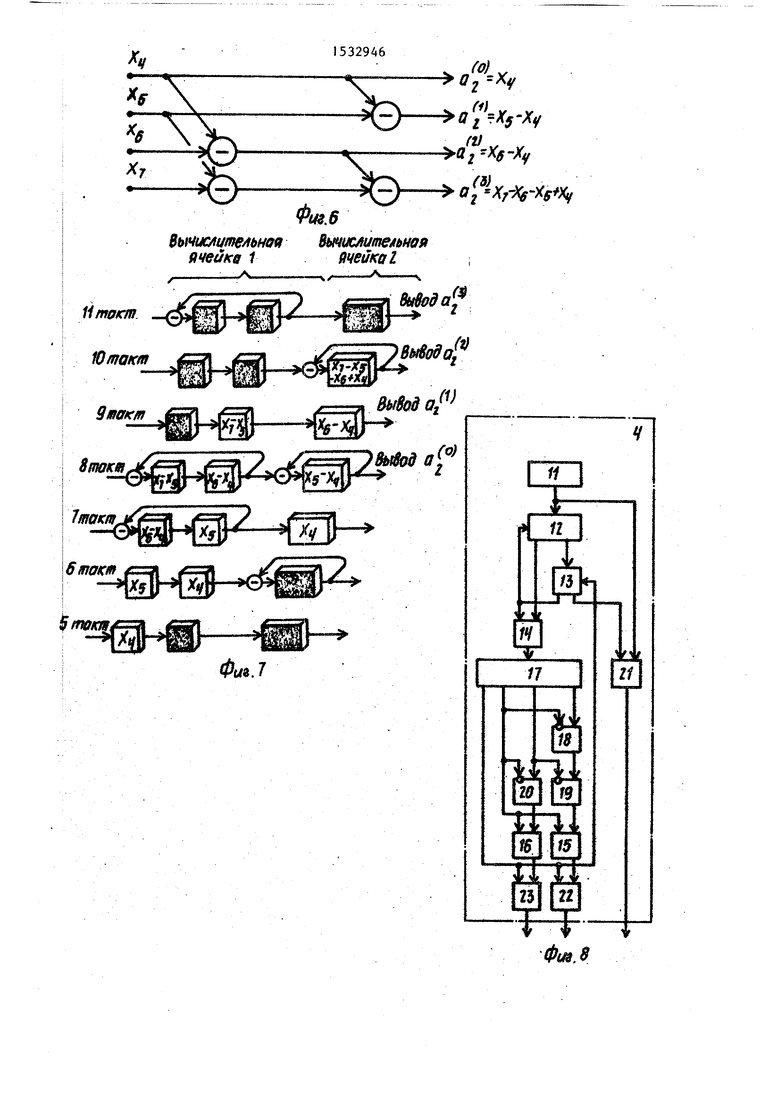
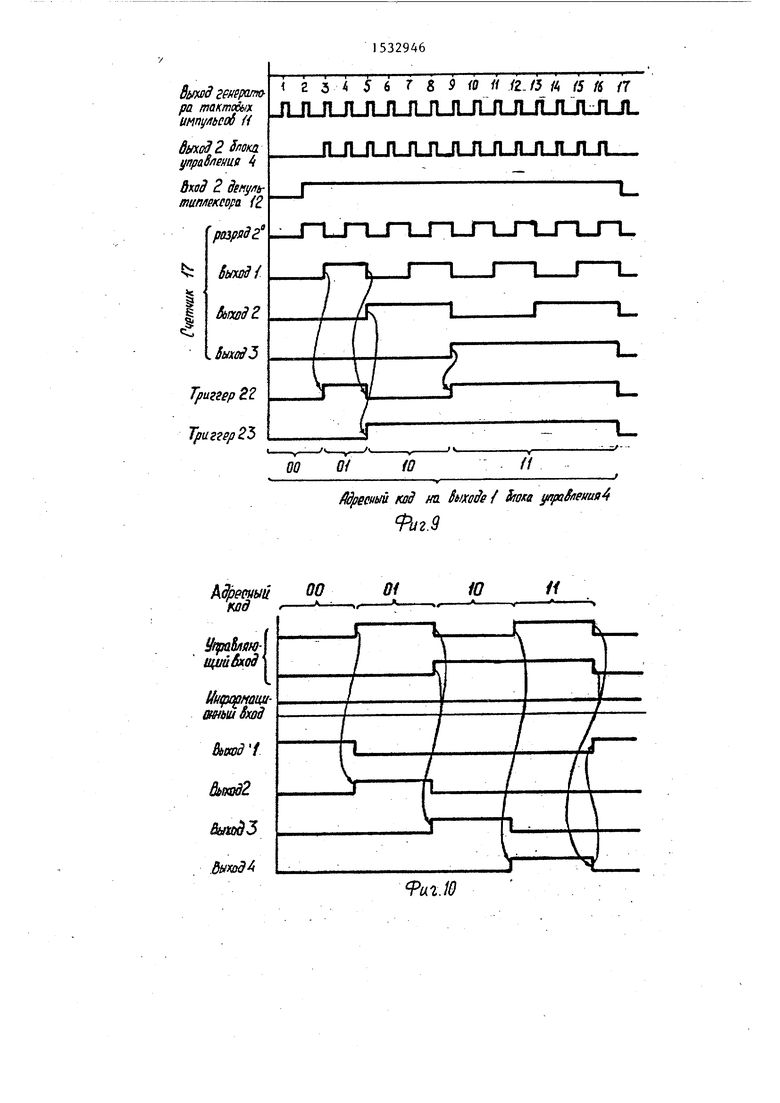
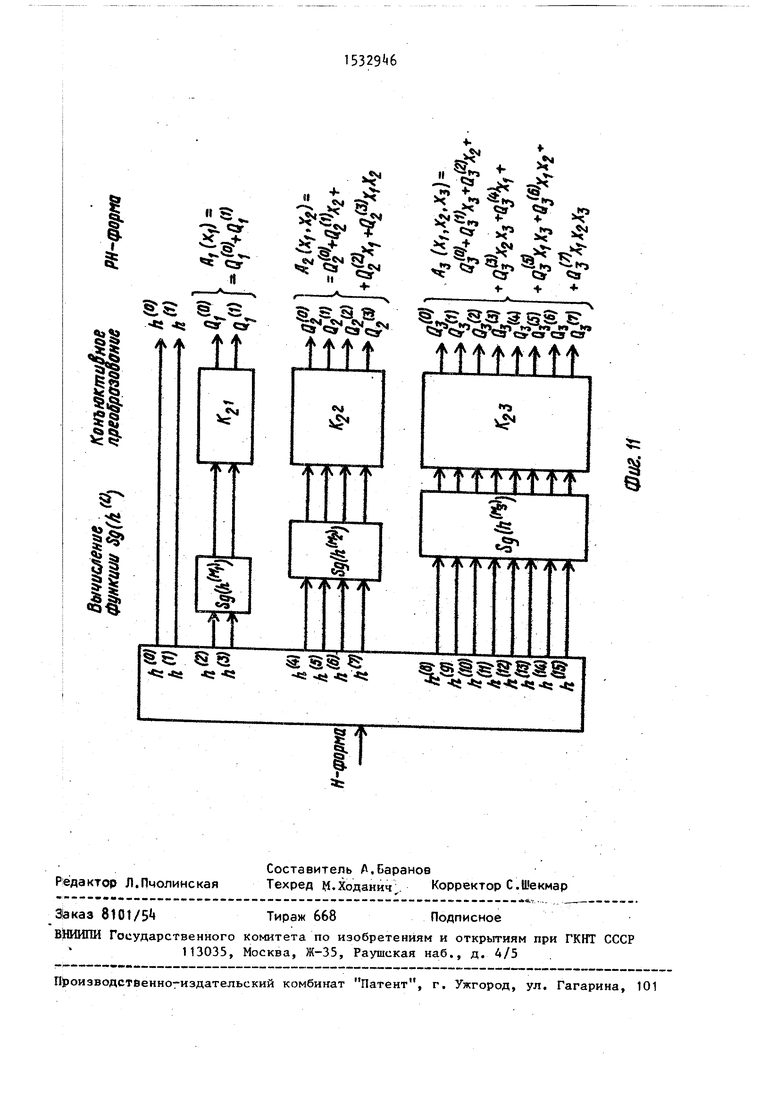
На фиг.1 представлена структурная схема устройства; на фиг.2 - схема блока нормировки{ на фиг.З структурная схема 1-го блока конъюнктивного преобразования на фиг. 4 и 5 - структурная схема и временная диаграмма работы 1-го блока конъюнктивного преобразования для i 2; на фиг.6 и 7 граф алгоритма и схема конъюнктивного преобразования в блоке конъюнктивного преобразования на фиг.8 и 9 - структурная схема и временная диаграмма работы блока синхронизации; на фиг. 10 - временная диаграмма работы коммутатора на фиг,11 - процесс формирования устройством РН-формы булевой функции f(х) четырех переменных.
Устройство содержит коммутатор 1, блок 2 нормировки, п-1 блоков 3 конъного узла, т.е. на вход вычитателя 7. С выхода вычитателя 7 (на другом входе вычитателя 7 - значение нуля), значение элемента So(h) поступает на вход регистра 9. Счетчик 10 переходит из состояния 00 в счетчике 01.
На шестом такте на вход вычитателя 7 поступает значение элемента 45 S(hts) (на другом входе вычитате- лй 7 значение нуля), с выхода вычитателя 7 значение элемента &з(Ь) поступает на вход регистра 9. Счетчик 10 переходит из состояния 01 в состояние 10. Таким образом, по окончании шестого такта в регистре 9 оказываются записанными значения Sq(lr) и Sg(h(5)/
На седьмом такте на вход вычитате50
ля 7 поступает элемент S(j(ht6)),
на
другой вход вычитателя поступает с выхода коммутатора 8 значение элемента S ( (на втором (управляющем) входе коммутатора 8 - высокий логиXjX.
юнктивного преобразования и блок k синхронизации.
Блок 2 нормировки обеспечивает преобразование спектральных коэффициентов Хаара h(1) (j 2,2nl) в соответствии с математической моделью (5) его функционирования, т.е. преобразует m-разрядный спектральный коэффициент Хаара h в двухразрядное значение функции нормировки Sa(htJ ) в соответствии с табл. 3.
Блок 2 нормировки содержит п-1 регистров 5 и п-1 элементов ИЛИ 6.
Первый блок 3 конъюнктивного преобразования содержит i вычислительных узлов, каждый из которых состоит из вычитателя 7, коммутатора 8 и регистра 9, и счетчик 10.
Рассмотрим работу п-1 блоков конъюнктивного преобразования 3
юнктивного преобразования 3
на примере 1-го блока конъюнктивного преобразования 3 () (табл. М. Предварительно счетчик 10 установлен в состояние 00. Введем обозначение xi
S«(h°) (j 2Т«-1).J
Первым рабочим тактом блока 3 конъюнктивного преобразования является пятый такт работы устройства (табл. t), На пятом такте значение
элемента Sij(h) поступает на инфор- мационный вход первого вычислитель
ного узла, т.е. на вход вычитателя 7. С выхода вычитателя 7 (на другом входе вычитателя 7 - значение нуля), значение элемента So(h) поступает на вход регистра 9. Счетчик 10 переходит из состояния 00 в счетчике 01.
На шестом такте на вход вычитателя 7 поступает значение элемента S(hts) (на другом входе вычитате- лй 7 значение нуля), с выхода вычитателя 7 значение элемента &з(Ь) поступает на вход регистра 9. Счетчик 10 переходит из состояния 01 в состояние 10. Таким образом, по окончании шестого такта в регистре 9 оказываются записанными значения Sq(lr) и Sg(h(5)/
На седьмом такте на вход вычитате
ля 7 поступает элемент S(j(ht6)),
на
другой вход вычитателя поступает с выхода коммутатора 8 значение элемента S ( (на втором (управляющем) входе коммутатора 8 - высокий логи915329 6
ческий уровень), а на его вход.пере10
дается значение элемента SaCh) с выхода регистра 9. Значение разности элементов (h(b) - (hM ) с выхода вычитателя 7 поступает на вход регистра 9.
Кроме того, значение элемента S(h) передается на выход первого вычислительного узла и далее на вход вычитателя 7 второго вычислительного узла (фиг.4). С выхода вычитателя 7 значение элемента Sg(h(4) поступает на вход регистра 9 (на другом входе вычитателя 7 - значение нуля). Счетчик tO переходит из состояния 10 в состояние 11.
На восьмом такте значение элемента Sg(h) поступает на вход вычитателя 7, на другой вход последнего с выхода коммутатора 8 передается значение элемента (h) (на втором (управляющем) входе коммутатора 8 - высокий логический уровень). С выхода вычитателя 7 значение разности Sq Sq() поступает на При этом значение элемента Sg с выхода регистра 9 передается на вход второго вычислительного узла и
10
вход регистра 9.
гмента Sg (h( )
читателя 7 поступает с выхода коммутатора 8 разность S(hw) - 5д(Ь(Ъ (на втором (управляющем) входе коммутатора 8 - высокий логический уровень). С выхода вычитателя 7 разность
sg( - sa(hts)) - 03() - Sa(h(bj поступает на вход регистра 9, с выхода которого коэффициент аг(1 Sg(h(6)) - SqCh) поступает на выход устройства. Счетчик 10 переходит из состояния 01 в состояние 10.
На одиннадцатом такте с выхода регистра 9 коэффициент а Sa(h(7)) - J5 - Sg(ht5) - (Sg(ht6) - S,(lX) передается на выход устройства.
Таким образом, на выход устройства в тактах с восьмого по одиннадцатый поступают значения коэффициентов а}.0, а, а«, а (табл. Ь). .
Блок синхронизации Ц (фиг.7Д для п k) содержит генератор Н тактовых импульсов, демультиплексор 12, регистр сдвига 13. первый 1, второй 15, (h(7))- 25 тРетий 16 элементы ИЛИ, счетчик 17,
первый 18, второй 19, третий 20, четвертый 21 элементы И, первый 22 и второй 23 триггеры.
Рассмотрим работу блока синхро20
далее на вход вычитателя 7. На другой 3Q низации для п « 4. Первоначально реаход вычитэтеля 7 с выхода коммутатора 8 поступает значение элемента 8(ЬМЪ (на втором (управляющем) входе коммутатора 8 - высокий логический уровень, а на пер вом - значение элемента (h(4))) с выхода регистра 9, С выхода вычитателя 7 значение разности S(ht5)) - S$(hM) поступает на вход регистра 9. При этом значение элемента Sq(h), являющееся коэффициентом а полинома ,х) , с выхода регистра 9 передается на выход устройства. Счетчик 10 переходит из состояния 11 в состояние 00. 1
В результате на девятом такте на вход вычитателя 7 с выхода первого вычислительного узла поступает значение разности (h(b) - Sj(h(4J) (на другом входе вычитателя 7 - значение нуля). С выхода вычитателя 7 значение
гистр 13 сдвига, счетчик 17, первый 22 и второй 23 триггеры установлены в нулевое состояние.
На первом такте импульс с выхода генератора 11 тактовых импульсов пос35 тупает на первый (информационный) вход демультиплексора 12. С первого выхода демультиплексора 12 сигнал (высокий логический уровень) поступает на регистр 13 сдвига и записывается в его
® первом разряде (на втором (управляющем) входе демультиплексора 12 низкий логический уровень). Первый 20 и второй 21 триггеры находятся в нулевом состбянии и на первом выходе блока синхронизации сформирован адресный код 00. На втором выходе блока 4 синхронизации находится низкий логический уровень, так как на первом входе четвертого элемента И 21 имеется низ45
разности S() - (hM)) передается 50кий логический уровень, на вход регистра 9. При этом коэффи- На втором такте импульс с выхода циент а S(ht5) - Sg(hЈ) с выхо-генератора 11 тактовых импульсов пода регистра Э поступает на выход уст-ступает на первый -(инйюомаиионный) ройства. Счетчик 10 переходит из сое -вход демультиплексора 12. С первого тояния 00 в состояние 01. 55выхода демультиплексора 12 (на его
На десятом такте на вход вычитате-втором (управляющем) входе - низкий ля 7 с выхода первого вычислительного узла поступает значение разности (t ) - S$(h(6). На другой вход вылогический уровень) высокий логический уровень сигнала поступает на регистр 13 сдвига, в котором произво10
низации для п « 4. Первоначально регистр 13 сдвига, счетчик 17, первый 22 и второй 23 триггеры установлены в нулевое состояние.
На первом такте импульс с выхода генератора 11 тактовых импульсов поступает на первый (информационный) вход демультиплексора 12. С первого выхода демультиплексора 12 сигнал (высокий логический уровень) поступает на регистр 13 сдвига и записывается в его
первом разряде (на втором (управляющем) входе демультиплексора 12 низкий логический уровень). Первый 20 и второй 21 триггеры находятся в нулевом состбянии и на первом выходе блока синхронизации сформирован адресный код 00. На втором выходе блока 4 синхронизации находится низкий логический уровень, так как на первом входе четвертого элемента И 21 имеется низ
кий логический уровень, На втором такте импульс с выхода генератора 11 тактовых импульсов поступает на первый -(инйюомаиионный) вход демультиплексора 12. С первого выхода демультиплексора 12 (на его
втором (управляющем) входе - низкий
логический уровень) высокий логический уровень сигнала поступает на регистр 13 сдвига, в котором произво
дится сдвиг в сторону старших разрядов. С первого выхода регистра 13 сдвига высокий логический уровень сигнала передается на второй (управляющий) вход демультиплексора 12 и на второй вход первого элемента ИЛИ 14. С выхода последнего сигнал поступает на счетный вход счетчика 17, в результате счетчик 17 переходит из состояния 0000 в состояние 0001. Таким образом, триггеры 22 и 23 остаются в исходном состоянии и на первом выходе блока синхронизации имеется адресный код 00. На втором выхо де блока управления присутствует низкий логический уровень, так как на первом входе четвертого элемента И 2 находится низкий логический уровень. На третьем такте импульс с выхода генератора 11 тактовых импульсов поступает на информационный вход демультиплексора 12. С второго выхода демультиплексора 12 (на его втором (управляющем) входе - высокий логический уровень) сигнал передается на первый вход первого элемента ИЛИ 1, с выхода которого сигнал поступает на счетный вход счетчика 17, последний переходит из состояния 0001 в состояние 0010. Сигнал с первого выхода счетчика 17 передается на первый вход первого элемента 18, а зате поступает с его выхода на первый вхо второго элемента И 19 (на втором (инверсном) входе первого элемента И 18 низкий логический уровень). С выхода второго элемента И 19 сигнал передается на первый вход второго элемента ИЛИ 15 (на втором (инверсном) входе второго элемента И 19 - низкий логи
Н,
- 8 2ll2f2 4-20200 2Y О 21Г 02т/ -2т{ ,
в полиномиальной форме Хаара РЫ(х).
На первом такте значение спектрального коэффициента Хаара 8 поступает на первый (информационный) вход коммутатора 1 (на втором (управляющем) входе которого - адресный код 00). С первого выхода коммутатора 1 значение htol 8 поступает на первый выход устройства (фиг.1).
На втором такте значение спектрального коэффициента h 2 аналогично значению hco- 8 передается на первой выход устройства.
На тактах с по 1б-й включительно значения спектральных коэффи10
15-
ческий уровень). С выхода второго элемента ИЛИ 15 сигнал поступает на первый вход первого триггера 22. Р результате триггер переходит в единичное состояние. Таким образом, на первом выходе блока 4 синхронизации формируется адресный код 01. Кроме того, в регистре 13 сдвига производится сдвиг информации, с второго выхода регистра 13 сдвига высокий логический уровень поступает на первый вход четвертого элемента И 21. На первый вход последнего с выхода генератора 11 тактовых импульсов передается сигнал, который далее с выхода четвертого элемента И 21 поступает на второй выход блока 4 синхронизации. Таким образом, на первом выходе блока 4 синхронизации формируется последовательность тактовых импульсов; отстающая на два такта от последовательности на выходе генератора 11 тактовых импульсов (фиг.9).
На семнадцатом такте блок 4 синхронизации переходит в исходное состояние. Этот период происходит под действием сигнала переполнения счетчика 17. Сигнал переполнения с чет- % вертого выхода счетчика 17 поступает на вторые входы (входы установки в нуль) первого 22 и второго 23 тригге20
25
30
ров, а также регистра 13 сдвига.
Рассмотрим функционирование устройства в совокупности составляющих его компонентов на конкретном примере.
Пусть необходимо представить булеву функцию f(x) четырех переменных, заданную своим спектром Хаара Rf
циентов Хаара с no h поступают на первый (информационный) вход коммутатора 1 и в соответствии с адресным кодом на втором (управляющем) входе последнего передаются на входы блока 2 нормировки, причем так, что на первый вход блока 2 нормировки поступают значения коэффициентов h(lJ т|2 и h -$2 На второй вход блока 2 нормировки передаются значения коэффициентов Ьи k, hC5 -2, h(6 0 и
h 7 2 и на третий вход блока 2 нормировки поступают значения коэффициентов 0, ht9 б, h 2{2t
ho« о h(n 2fi- h«5 2{Г и 0.
В блоке 2 нормировки формируются значения х. (j 2,15) функции S (h1-)) в соответствии с математической моделью (5):
-1, hlJ 0-,
0,hu) fe О,
1,hu 0,
)
т.е. формируются следующие значения
Х6
х«о
х«4
О, х7
Ь х«
1, Xi5
1, хл
1, х«
0, О,
Ь Х5 -1
О, хэ О,
В первом блоке конъюнктивного пре 15 образования 3 формируются значения
4
1, -1,коэффициентов и а1, в соответствии с математической моделью (6)
А, К4,- S9( Ка.хгх,,
S
Следовательно, полином A,,(xf) имеет вид: АДх 1
Во втором блоке 3 конъюнктивного преобразования формируются значения
АЈ П ) Следовательно, полином Ав(х,,х€) имеет вид: Ай(х ,х ) 1 + х - x4Xfc В третьем блоке 3 конъюнктивного преобразования формируются значения
Кгъ-5 з( К4э-Сх4х9х)0 х„ х„ XHX,
0000000 1000000 0100000
-1-1 1 гр О О О 0001000
-100-1100
0-10-1010
1 1-1 1-1-1 1
Следовательно, полином А«,(х,Хг, х.з) имеет вид:
Ад(х,,Хв,Хэ) X,j - XjXj + Х4 -
- 2х,Х2, + - 2х(х,гх,).IJQ
Табл. k и 5 иллюстрируют вычислительный процесс в первом, втором и третьем блоках 3 конъюнктивного преобразования.
Формула изобретения
С первого выхода блока 2 нормировки значения XL и хЈ передаются на вход первого блока 3 конъюнктивного преобразования 3, с второго выхода блока 2 нормировки значения х4, xg х и х f поступают на вход второ- - го блока 3 конъюнктивного преобразования и с третьего выхода блока 2 нормировки значения х, хл, х(0 , х( , х, х4,, и х(5 поступают на тре- тий блок 3 конъюнктивного преобразования (табл. 5).
В первом блоке конъюнктивного пре- образования 3 формируются значения
коэффициентов и а1, в соответкоэффициентов и а1, в соответ
ствии с математической моделью (6)
«-0 п
,W
и а
3)
в соответствии с математической моделью (6):
25
коэффициентов aj,° , а( , aial, а -«I „tO „(6) 5--
af,
«Т а г
в соответствии
Ji °,
математической моделью (о):
Q
5
блок конъюнктивного преобразования и блок синхронизации, отличающееся тем, что, с целью расширения класса решаемых задач за счет реализации преобразования булевых функций в арифметическую полиноминальную форму Хаара, в него введены п-2 (п - число переменных функции) блоков конъюнктивного преобразования, блок нормировки, коммутатор и первый выход блока синхронизации подключен к управляющему входу коммутатора, первый выход которого является пер15
Јым информационным выходом устройства, информационным входом которого Является информационный вход коммута- fopa, i-й (i 2,п) выход которого Подключен к (1-1)-му информационному ходу блока нормировки, (1-1)-и вы- од которого подключен к информационному входу (1-1)-го блока конъюнктив- юго преобразования, выход которого является 1-м информационным выходом устройства, а второй выход блока син- кронизации подключен к тактовым входам блока нормировки (i-1)-го блока конъюнктивного преобразования.
10
20
15
30
Таблица 1
UK
Примечай . Xj S,(hu/) (j 2,2Я-Т)
17
18
ТаблицаЗ
Т«бйиц Ц
1 Х«
.«
х,-х, хи-х,
19
15329 6
h
блок 3 конъюнктивного преобразования
I Копну- I Регистр 9 } Копну- I Информационный ммод 1| 1 татор 8
,
19 20
1
Х„.-Х,0-Х,г«С, XifX« Х„-Х|
х„-х„-х(,+х,,-х,Х,-Х„,-Х,г+Хв Х,-Х, w « +
Хц-Xe - -X it Х |
22 23
1}
I
Ч F
Tjfb-
20 Продолжение табл.5
-
-х„-хгх +х,
,««
Х.«-Х, а
х«-х,
.
-х«.-х,-х„+х,
Хц-Xe - -X it Х |
-ХЛ+Хв-Хц -Х„- ад «А -X(,.-X, , XM-X«-XW4X, ain - Х -Х„-Х„+Х«- -Х,
Ввод
хЧ
Тактовые импульсы
1-и8ыход cwwt/w Ю
I-и Выход счетчикд Ю
.V
,., 7
;
/
««.У
Ы
ft
5-Х
1532946
Вьнимительноя Вычислительная
ячейке 1Ячейка I
Ьta fa
V V
0Z rJj-xfy Дг
Вывод ог(1}
,(о)
г з 56 r s $ го я /г./з « ts /v a
иииьллии ruuuuuuuuuuuL
разряде
е
-г
SbOUtff
6ыход2 . йшоЗЗ Триггер 22 Триггер 2Ъ
00
Of
Мртый код
00
typa&iffw- щийбход
Умрфнаци- втыийход
ВытдЧ дыхвд2 &/ш)3 дыъздЬ
/О
/7
шл /и ла Выходе f Sroxa ynpofoeuua4 2.9
01
ю
а
Фиг.Ю
I
Т
| Преобразователь формы представления логических функций | 1983 |
|
SU1124281A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Анализатор спектра | 1981 |
|
SU1001107A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1989-12-30—Публикация
1988-04-12—Подача