В предлагаемом логарифмическом арифмометре все вычислительные действия над числами производятся посредством сложения и вычитания не линейных отрезков, а площадей определенных участков счетной плоскости, выполненной в виде таблицы, разделенной на 9 логарифмических полей с нанесенными на ней антилогарифмами.
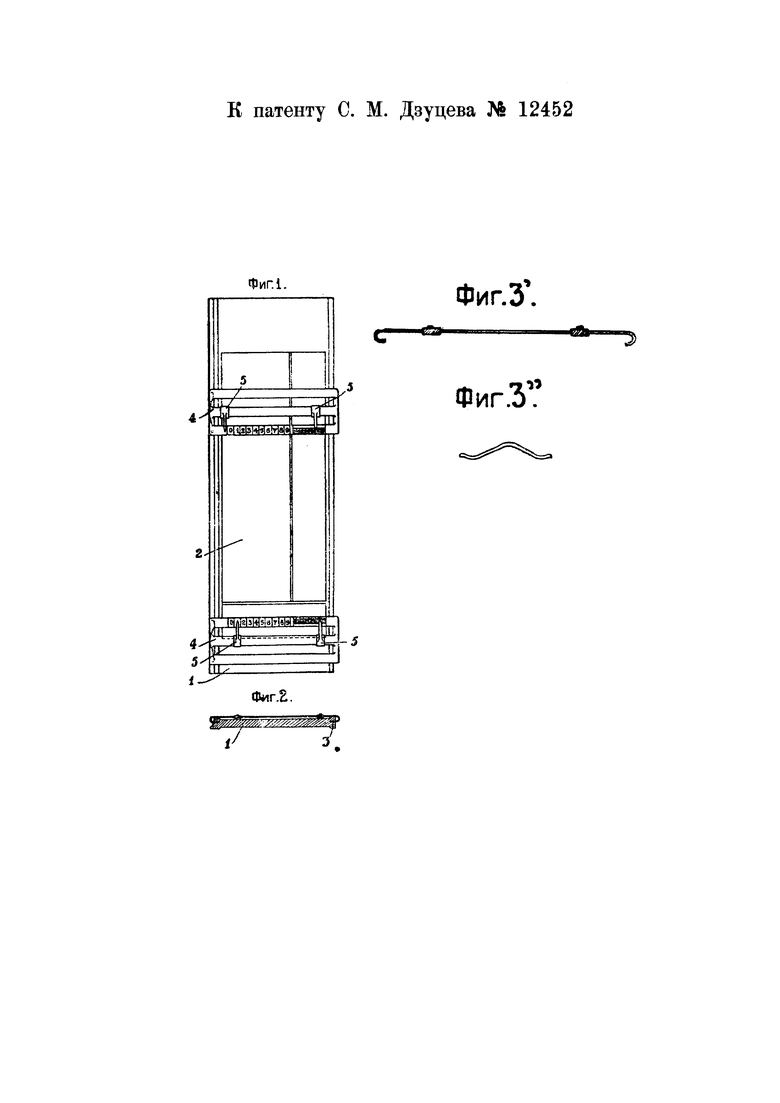
На чертеже фиг. 1 изображает вид арифмометра сверху; фиг. 2 - вертикальный ее разрез; фиг. 3- движок с указателями, фиг. 3′ и 3′′ - отдельные детали арифмометра; фиг. 4 - счетная плоскость арифмометра.
Логарифмический арифмометр состоит из планшета 1, снабженного счетной плоскостью, выполненной в виде таблицы антилогарифмов 2 (см. фиг. 4), разделенной на 9 логарифмических участков или полей.
Планшет снабжен системой двух движков 4, 4 с двумя передвижными указателями 5, 5 на каждом, предназначенной для определения места нахождения площадок с числами, над которыми должны производиться соответственные действия. Движки могут перемещаться вдоль планшета в пазах 3.
I. Логарифмирование. Вся плоскость логарифмического арифмометра разбита горизонтальными ломанными линиями на 9 полей, каждое из которых заключает четырехзначные числа, начинающиеся соответственно цифрами 1, 2, 3…9, поэтому при отыскании некоторого четырехзначного числа следует останавливать внимание на том из девяти логарифмических полей, порядок которого указан первой цифрой искомого числа; что же касается остальных цифр последнего, то таковые также указаны в пределах того же поля.
Пример. - Лог. 1459=x, найти x. Данное число имеет своей первой цифрой единицу; поэтому, обращая внимание на последние три (459) будем искать его в пределах первого поля в столбце 0, где вместо искомого числа находим два ближайших к нему, из всех находящихся в этом столбце чисел, одно из которых стоит в 16-й строке и равно 1445, меньшему нашего числа, а другое в 17-й строке и равно 1479, большему того же числа. Поэтому число наше следует ожидать в 16-й строке, несколько правее, где находим 1459 в том столбце, который помечен на движках 4 цифрой 4. Число 16, указывающее порядок строки, и цифра 4, отмечающая порядок столбца, на пересечении которых найдено данное число, являются первыми тремя цифрами мантиссы логарифма искомого числа; что же касается четвертой цифры, то таковая всегда равна 0. Итак лог. 1459=3.1640.
Примечание 1. Все числа, непосредственно указанные в основных столбцах, имеют мантиссы логарифмов, всегда окончивающиеся цифрой 0.
Интерполирование. Отыскивая мантиссы логарифмов чисел, не указанных непосредственно в основных столбцах, следует пользоваться одновременно, как основными, так и вспомогательными столбцами.
Пример. - Лог. 2320=x, найти x.Следуя изложенному выше приему находим во втором поле на пересечении 36-й строки с 5-м основным и 5-м вспомогательным столбцами вместо числа 2320, число 2317 и его поправку, равную трем единицам (2320=2317+3). Итак лог. 2320=3.3655.
Примечание 2. Четвертая цифра мантиссы всегда стоит на бегуне против того столбца, где указана поправка.
II. Антилогарифмирование. Чтобы найти число имеющее данный четырехзначный логарифм, необходимо один из движков 4 установить на строке, порядок который отмечен первыми двумя цифрами мантиссы данного логарифма, а передвижные указатели 5 движка 4 перевести на столбцы, порядок которых указан двумя последними цифрами мантиссы.
Пример. лог. x=2.5145, найти x. Установив движок 4 на 51-й строке, а указатель 5 на четвертом основном и пятом вспомогательном столбцах, находим число 3266+4-3270. Принимая же во внимание характеристику 2, имеем: х=327.0.
III и IV. Сложение и вычитание. Являются они действиями подсобными и могут быть уяснены при производстве умножения и деления.
V. Умножение Пример. - 1.268×13.61=? Установив верхний движок 4 против меньшего множителя 1.268, а нижний против большего 13:61, складываем цифры, указывающие порядок столбцов, заключающих данные множители (3+4=7).
Переводим указатель так, чтобы он закрыл полученную цифру 7 нижнего движка. Складывая далее числа указывающие порядок строк в которых стоят данные множители, получим: 10+13=23. Установив нижний движок 4 на 23-й строке, получим против указателя 5 искомое произведение, равное 17.26. Итак 1.268×13.61=17.26.
VI. Деление. Пример. - 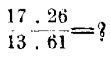 Для отыскания частного этих чисел один из движков 4 следует установить на 23 строке, а его указатель на 7-м столбце, где и находим делимое 1726. Верхний движок 4 устанавливаем против 13-й строки, а его указатель 5 против порядок столбцов и строк получим на 10-й строке искомое частное. Имеем:
Для отыскания частного этих чисел один из движков 4 следует установить на 23 строке, а его указатель на 7-м столбце, где и находим делимое 1726. Верхний движок 4 устанавливаем против 13-й строки, а его указатель 5 против порядок столбцов и строк получим на 10-й строке искомое частное. Имеем: 
VII. Возведение в степень. Пример. - 1.2653=? Установив движок 4 на число 1265 и умножив число 2, указывающее порядок столбца, на показателя степени 3 получим: 2×3=6. Установив далее указатель 5 движка 4 на 6-м основном столбце, умножаем число 10, указывающее порядок строки, на 3 и получим 30(10×3=30). Переводя движок 4 на 30-ю строку, находим в 6-м основном столбце 3-ю степень данного числа. Итак имеем: 1.2653=2.023.
VIII. Извлечение корня. Вычислить Разделив число 30 и 6, указывающие порядок строки и столбца, на показателя 3, получим новые числа 10 и 2, показывающие порядок строки и столбца искомого корня. Установив движок 4 и его указатель на эти строку и столбец получим
Разделив число 30 и 6, указывающие порядок строки и столбца, на показателя 3, получим новые числа 10 и 2, показывающие порядок строки и столбца искомого корня. Установив движок 4 и его указатель на эти строку и столбец получим 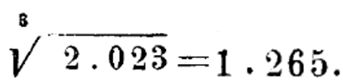
Проверка производится обратным умножением вновь полученной мантиссы на показателя корня.
| название | год | авторы | номер документа |
|---|---|---|---|
| Логарифмический арифмометр | 1929 |
|
SU15089A1 |
| Логарифмические счеты | 1922 |
|
SU1340A1 |
| Цилиндрическая логарифмическая счетная линейка | 1926 |
|
SU9921A1 |
| Логарифмическая счетная линейка | 1956 |
|
SU117763A1 |
| Счетный логарифмический прибор | 1956 |
|
SU113214A1 |
| Счетный логарифмический диск | 1931 |
|
SU30189A1 |
| Дисковая логарифмическая линейка для определения приращений | 1979 |
|
SU773633A1 |
| Логарифмический счетный прибор | 1933 |
|
SU39446A1 |
| Логарифмическая счетная линейка | 1932 |
|
SU31677A1 |
| Устройство для определения наивыгоднейших режимов резания на металлорежущих станках и для решения других задач, сводящихся к решению системы уравнений вида b1^y1=(a1^x1*a2^x2*…*an^xn)/(b2^y2*b3*…*bn^yn) | 1957 |
|
SU122640A1 |

Логарифмический арифмометр, характеризующийся тем, что счетная плоскость, в виде таблицы, разделенной на 9 логарифмических участков или полей с нанесенными на них антилогарифмами, снабжена системой двух движков с двумя передвижными указателями на каждом, служащей для определения местонахождения площадок с числами, над которыми должны производиться соответственные действия.
Авторы
Даты
1929-12-31—Публикация
1928-09-14—Подача