fO
J5
Изобретение относится к автоматике и может быть использовано в системах передачи информации, в частности в системах синхронизации.
Цель изобретения - расширение области применения за счет обеспечения возможности декодирования последовательностей Голда.
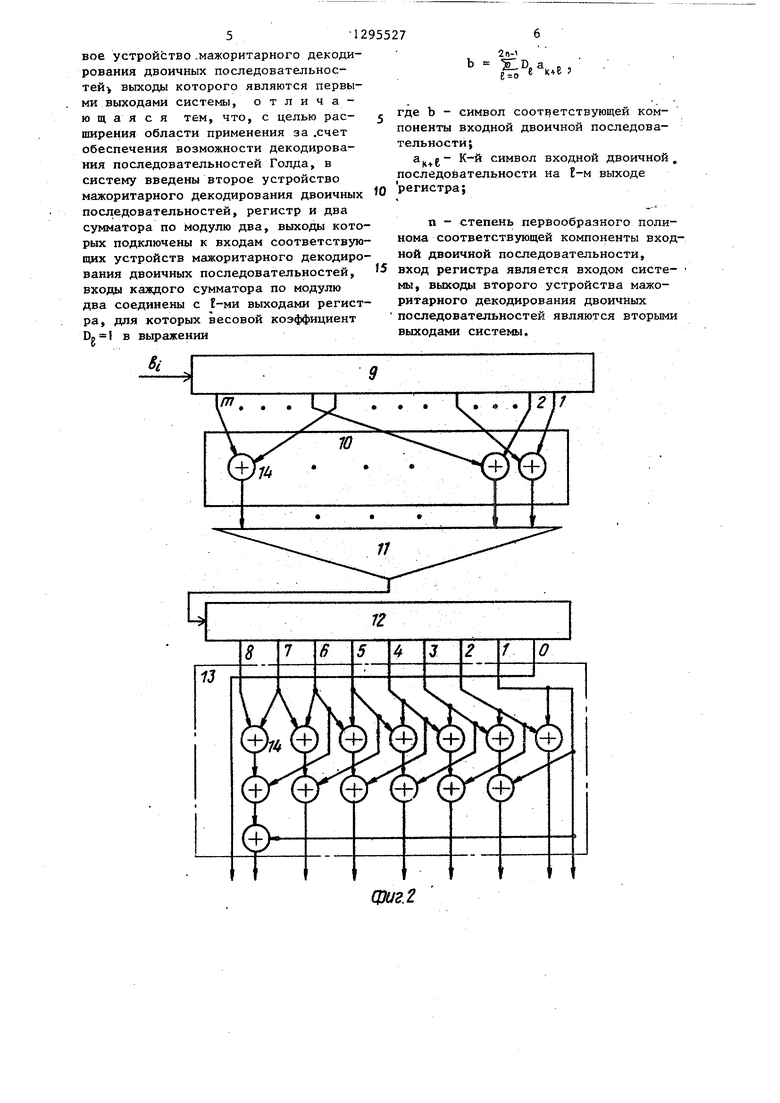
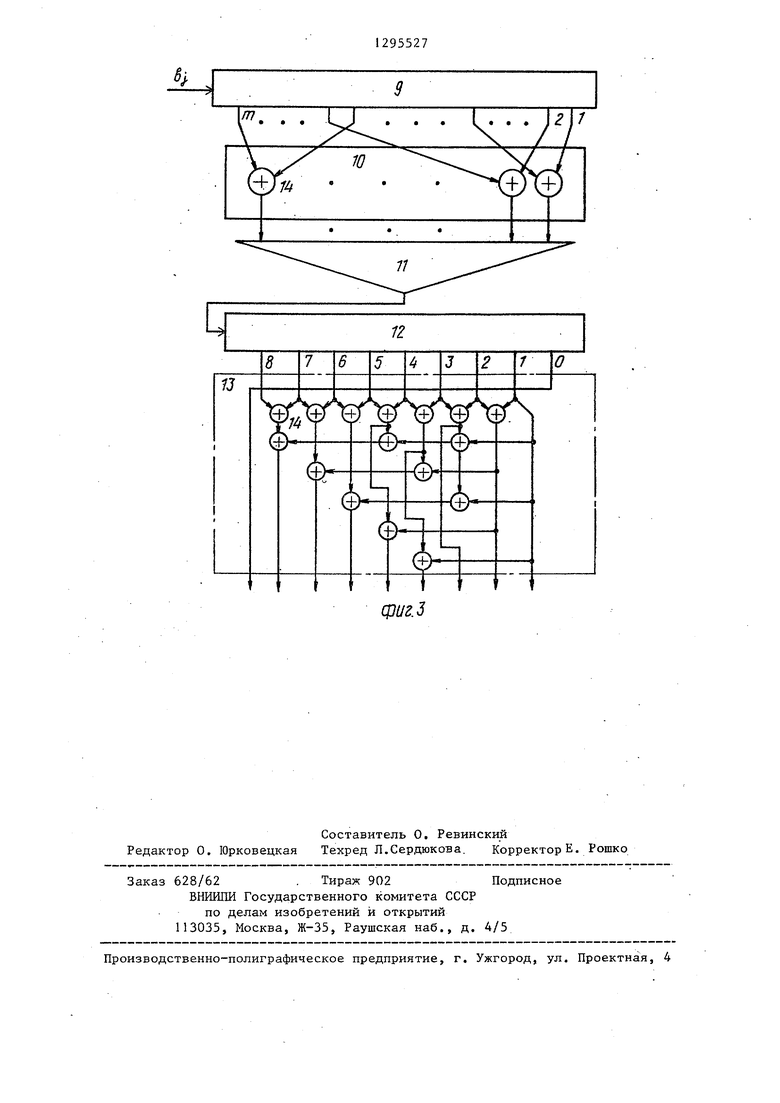
На фиг. 1 представлена блок-схема системы декодирования двоичных последовательностей; на фиг. 2 и 3 - функциональные схемы соответственно первого и второго устройств мажоритарного декодирования двоичных последовательностей.
Система декодирования двоичных последовательностей содержит регистр
I,первый и второй сумматоры 2 и 3 по модулю два, первое и второе устройства 4 и 5 мажоритарного декодиро- вания двоичных последовательностей, вход 6, первые и вторые выходы 7 и 8.
Устройства 4 и 5 мажоритарного декодирования двоичных последовательностей включают в себя (фиг. 2 и 3) входной регистр 9, блок 1Q проверочных сумматоров, мажоритарный элемент
I1,дополнительный регистр 12 и определитель 13 координат, Блоки 10 и 13 выполнены на сумматорах 14 по модулю два, соединенных в соответствии с полиномами тех М-последовательностей, для декодирования которых пред25
30
ностей Голда, состоящее из кодовых последовательностей. Структура предлагаемой системы и принцип ее работы универсальны, т.е. справедливы для любых пар полиномов fj (х) и ) п-й степени, порождающих последовательности Голда. Б общем виде полиномы (к) и их сопровождающие матрицы Н имеют вид
f(x)., +...+С,х+С„;
00... ОСо 10...ОС, Н 01...0С2
00...1С„
где С - весовые коэффициенты, принимающие значение О или 1.
Система декодирования двоичных последовательностей позволяет определить по входным символам последовательности Голда, поступающим на регистр 1, символы порождающих М-последовательностей, описываемых полиномами f(х) и ), а также .все другие координаты ненулевых элементов полей GF(2).
Пре ртагаемая система способна без перестройки ее структуры, и параметров декодировать 511 кодовых последовательностей Голда (в общем случае 2 -1)., поступающих на ее
назначены устройства 4 и 5, На фиг.2 и 3 даны примеры реализации устройств35 вход. Для системы декодирования но- 4 и 5 для полиномов соответственно мера отводов регистра 1 и его раз- f, (х)х - -х +х +х + 1 и f2{x) рядность находятся следующим образом и 5 4 « (методика нахождения одинакова для
5Г t X T 5fT Vr 4 V4 4 l
. л л л л .. 9 я т г любых пар порождающих М-последова- Пара полиномов f, (х)х +х«+х +х тельностей).
.и
р f2(x)x +X +X +x +x +x4x%X +1
описывает М-последовательности , по рождающие семейство последовательПервообразные полиномы f(x) и f j, (х) в данном случае имеют сопровождающие матрицы
,
000000001 1 00000000 010000001 001000000 000100000 00001 0000 000001000 000000101 00000001 1
ностей Голда, состоящее из кодовых последовательностей. Структура предлагаемой системы и принцип ее работы универсальны, т.е. справедливы для любых пар полиномов fj (х) и ) п-й степени, порождающих последовательности Голда. Б общем виде полиномы (к) и их сопровождающие матрицы Н имеют вид
f(x)., +...+С,х+С„;
00... ОСо 10...ОС, Н 01...0С2
00...1С„
где С - весовые коэффициенты, принимающие значение О или 1.
Система декодирования двоичных последовательностей позволяет определить по входным символам последовательности Голда, поступающим на регистр 1, символы порождающих М-последовательностей, описываемых полиномами f(х) и ), а также все другие координаты ненулевых элементов полей GF(2).
Пре ртагаемая система способна без перестройки ее структуры, и параметров декодировать 511 кодовых последовательностей Голда (в общем случае 2 -1)., поступающих на ее
вход. Для системы декодирования но- мера отводов регистра 1 и его раз- рядность находятся следующим образом (методика нахождения одинакова для
Первообразные полиномы f(x) и f j, (х) в данном случае имеют сопровождающие матрицы
г
000000001 100000001 010000001 001000001 000100001 000010001 00000 100 1 о о 0000 1 00 000000011
а векторы-столбцы координат i-ro и j-ro символов первой и второй компонент, полиномы f ( (х) и f2(х), в общем случае имеют вид Х;(х°, xj,
n-t
) , Xj(x° , x
n-1
Ч
где а, Ь; и Ь: - соответственно К-: символ последовательности Голда, i-й и j-й символы М-последовательностей.
Можно составить систему из 2п уравнений
к. .1 +bj,, ;
и
где X. и X j - К-ые,координаты i-го и j-ro символов первой и второй компонент соответственно, KGLO, n-lj ; t - знак транспонирования
Символы некоторой последовательности Голда можно рассматривать как результат суммирования по модулю два символов двух сдвинутых относительно друг друга порождающих М-пос- ледовательностей
+bj ,
+bj.E
H+2n-i где каждый из символов М-последовательностей в npEBbix частях уравнений можно определить с помощью матриц Н, и Н2 через совокупность координат 1- го и JTO символов последовательностей.
Так, используя значение первых строк матрии 1 Н,- и Hj в некоторой степени t, соответствующей номеру уравнения системы из 2п уравнений , 2n-ll), это уравнение можно записать
,.е „е
ак.., х.н,,.х.,
где И и Hj, - первая строка мат45
I
риц Н, и Hj соответственно.
С учетом Toroj что b|.g. ,
для любого , решение системы уравнений позволяет определить 0 значение текущих символов порождающих М-последовательностей через совокупность символов последовательности Голда, записанных в регистр 1, т.е. реишть задачу декодирования этой последовательности. Символы М-после- довательностей, описываемые полиномами f,(х) и f2(х), находятся с помощью Система декодирования двоичных
Использование устройств 4 и 5 м жоритарного декодирования позволяе обеспечить требуемую вероятность ошибки определения всех координат элементов обеих компонент-.
Таким образом, система дает воз можность декодировать не только от дельные М-последовательности, но и порождаемые ими последовательности Голда.
Формула изобретени
выражении
1295527
1-i
;
.рв
..
4 ак.,,®В,о a,®D6-a,j,©D5«
a,,©D
a.,3®Dio . ,. a,.
Оба соотношения для символов b
а,
a.Mo®De
ак.б®05
и
10
;
5
20
25
30
35
40
.
можно записать в общей для этих
45
I
0ю Система декодирования двоичных
символов компактной форме
20-1
Ь Dg-a р,
, 0
где Ъ - символы М-последовательностей причем из развернутых соотношений для Ь и bj следует, что для символов первой М-последовательности, описываемой полиномом f (х), весовые коэффициенты при , 3, 4, 5, 6, 10, 3, для второй - при 3, 4, 5, 6, 10, 13, а для других значе- НИИ F весовые коэффициенты равны нулю для обеих компонент.
Система декодирования двоичных последовательностей работает сле- образом.
Символы последовательности Голда последовательно поступают с входа 6 на регистр 1, с выходов которого они подаются на входы сумматоров 2 и 3 по модулю два.
Текущие символы b; и Ь: с выходов сумматоров 2 и 3 поступают на соответствующие устройства 4 и 5 мажоритарного декодирования двоичных последовательностей. Каждое из устройств 4 и 5 настроено на обработку своей М-последовательности5 устройство 4 - на обработку компоненты, описываемой полиномом f (х), а устройство 5 - полиномом f(х). Одна пара полиномов порождает последовательностей Голда, что обеспечивает декодирование всех этих последовательностей без перестройки системы,
Использование устройств 4 и 5 мажоритарного декодирования позволяет обеспечить требуемую вероятность ошибки определения всех координат элементов обеих компонент-.
Таким образом, система дает возможность декодировать не только от- дельные М-последовательности, но и порождаемые ими последовательности Голда.
Формула изобретения
последовательностей, содержащая пер5-12
вое устройство .мажоритарного декодирования двоичных последовательнос- тей выходы которого являются первыми выходами системы, отличающаяся тем, что, с целью расширения области применения за .счет обеспечения возможности декодирования последовательностей Голда, в систему введены второе устройство мажоритарного декодирования двоичных последовательностей, регистр и два сумматора по модулю два, выходы которых подключены к входам соответствующих устройств мажоритарного декодирования двоичных последовательностей, входы каждого сумматора по модулю два соединены с -ми выходами регистра, для которых весовой коэффициент Dg 1 в выражении
2п-1
ж:п,
е 5
где b - символ соответствующей компоненты входной двоичной последовательности;
к+в К-й символ входной двоичной, последовательности на Е-м выходе регистра;
п - степень первообразного полинома соответствующей компоненты входной двоичной последовательности, вход регистра является входом системы, выходы второго устройства мажоритарного декодирования двоичных последовательностей являются вторыми выходами системы.

| название | год | авторы | номер документа |
|---|---|---|---|
| Система декодирования двоичных последовательностей | 1991 |
|
SU1807563A1 |
| Устройство мажоритарного декодирования двоичных последовательностей | 1982 |
|
SU1106014A1 |
| Устройство для декодирования двоичных последовательностей | 1987 |
|
SU1431075A2 |
| Кодек несистематического сверточного кода | 1988 |
|
SU1580567A1 |
| Мажоритарное декодирующее устройство | 1975 |
|
SU538502A1 |
| Устройство для исправления ошибок в информации, закодированной циклическим кодом | 1974 |
|
SU512589A1 |
| СПОСОБ СИНДРОМНОГО ДЕКОДИРОВАНИЯ ДЛЯ СВЕРТОЧНЫХ КОДОВ | 2004 |
|
RU2282307C2 |
| СПОСОБ ПЕРЕДАЧИ ДИСКРЕТНОЙ ИНФОРМАЦИИ В РАДИОЛИНИИ С ПСЕВДОСЛУЧАЙНОЙ ПЕРЕСТРОЙКОЙ РАБОЧЕЙ ЧАСТОТЫ | 2002 |
|
RU2212105C1 |
| Кодек несистематического сверточного кода | 1990 |
|
SU1714812A1 |
| СПОСОБ ПЕРЕДАЧИ СООБЩЕНИЙ В СИСТЕМАХ СВЯЗИ | 2003 |
|
RU2260915C2 |
Изобретение относится к автоматике. Его использование в системах передачи информации, в частности в системах синхронизации, позволяет расширить область применения за счет обеспечения возможности декодирования последовательностей Голда. Система декодирования двоичных последовательностей содержит устройство 4 мажоритарного декодирования двоичных последовательностей. Введение еще одного такого устройства 5, регистра 1 и сумматоров 2, 3 по модулю два обеспечивает разложение последовательности Голда на порождающие М-по- следовательности с раздельным декодированием каждой из них. 3 ил. СЛ У1 И рЮ Фиг. 1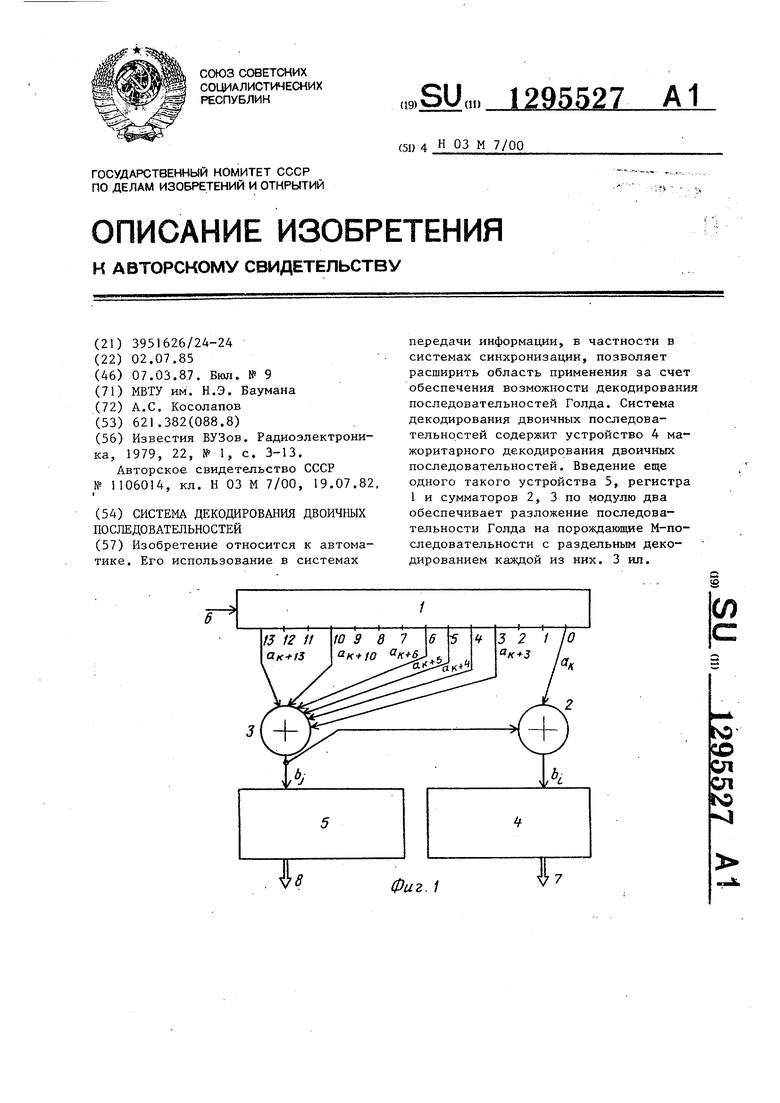
фиг.2
фиг. 5

| Известия ВУЗов | |||
| Радиоэлектроника, 1979, 22, № 1, с | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Устройство мажоритарного декодирования двоичных последовательностей | 1982 |
|
SU1106014A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
Авторы
Даты
1987-03-07—Публикация
1985-07-02—Подача