Изобретение относится к вычислительной технике и предназначено для использования в ЦВМ.
Цель изобретения - расширение функциональных возможностей за счет вычисления значений функций нескольких переменных.
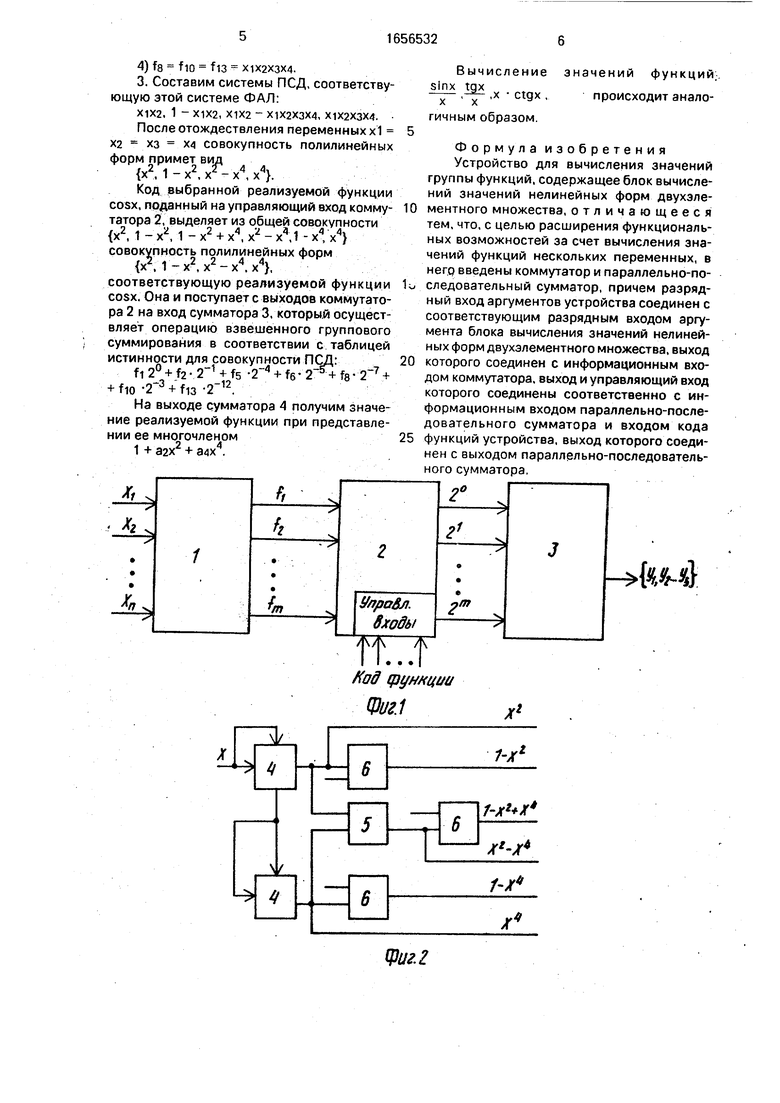
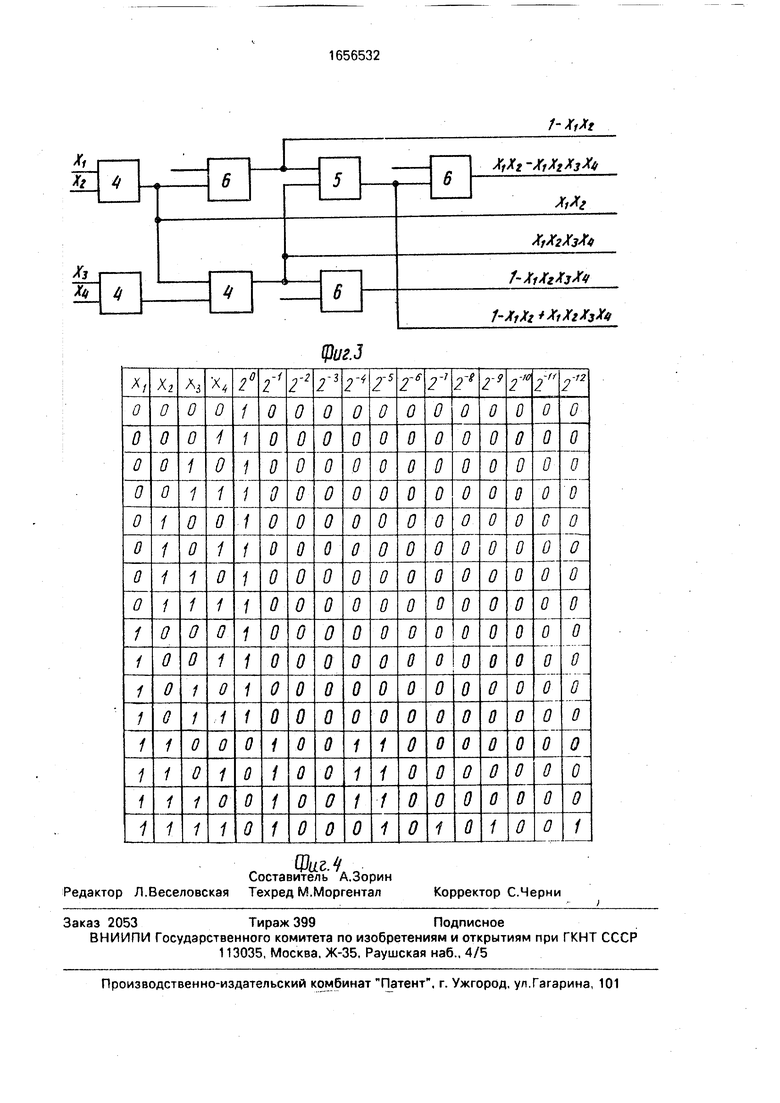
На фиг. 1 представлена блок-схема устройства; на фиг.2 - схема блока вычисления значений полилинейных форм двухэлементного множества для функций одной переменной; на фиг. 3 - то же, для случая четырех переменных; на фиг. 4 - таблица истинности для совокупности нелинейных форм, сохраняющих двухэлементное множество чисел.
Устройство (фиг. 1) содержит блок 1 вычисления значений полилинейных форм двухэлементного множества 1, коммутатор 2, параллельно-последовательный сумматор 3.
Блок 1 для случая одной переменной (фиг. 2) и случая четырех переменных (фиг. 3) содержит умножители 4, сумматор 5. вычи- татели 6 из единицы.
Устройство позволяет реализовать преобразование любого степенного многочлена и полилинейной формы по следующему алгоритму:
1)степенной многочлен или полиноминальная форма, т.е сумма конечного
числа членов вида ai, a2...nxT1 xf2... ...xnmn приводит к полилинейной форме путем введения дополнительного числа переменных, путем представления каждой степени xi ввидехссхц Х|2 . . х,т где хц -х.-. вновь введенные переменные;
2)полилинейная форма при значениях коэффициентов и переменных, представленных в двоичной позиционной системе счисления конечным числом разрядов, может быть поелставлена в виде
-mi
Р(х„Хг,... п,-21 (ХоХг,..-,„)
i-Г,
при 2 m1 Ф 2,где h (xi. хгxn) полилинейная форма, сохраняющая двухэлементное множество (ПСД), т.е. такая форма, которая при значениях аргументов, взятых из двухэлементного множества чисел Е2 - {0,1}, также принимает значения из {0,1};
сл
С
о ел о ел
OJ
го
3) ПСД Fi (xi, X2xn) при любых значениях переменных XL X2хп, представленных в виде: ,-Ј.2,
Совокупность ФАЛ, соответствующая
полилинейной форме, т.е. сумме, состоящей
из членов вида aixi, xi2 ... xi| . где 1 ij N,
не зависит от значения не равных нулю коэффициентов ао, a2...ai.
Окончательно имеем

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления булевых функций | 1984 |
|
SU1242928A1 |
| Устройство для вычисления коэффициентов полинома линейных булевых функций | 1990 |
|
SU1725214A1 |
| Устройство для вычисления симметрических булевых функций | 1989 |
|
SU1684792A1 |
| Устройство для вычисления симметрических булевых функций | 1991 |
|
SU1833860A1 |
| Универсальный логический модуль | 1983 |
|
SU1148024A1 |
| Многофункциональный модуль | 1981 |
|
SU966689A1 |
| Устройство для вычисления систем булевых функций | 1989 |
|
SU1644126A1 |
| Многофункциональный логический модуль | 1989 |
|
SU1667046A1 |
| Устройство для вычисления спектра сигналов | 1986 |
|
SU1383392A1 |
| Многофункциональный логический модуль | 1985 |
|
SU1290290A1 |

Изобретение относится к вычислительной технике и предназначено для использо- вания в ЦВМ. Цель изобретения - расширение функциональных возможностей за счет вычисления значений функций нескольких переменных Это достигается введением в структуру, содержащую блок вычисления значений группы полилинейных форм, коммутатора и последовательно соединенного с ним параллельно-последовательного сумматора. 4 ил
определяется по формуле
00 00
, n)-Z:2- 2: ...Z:2-ln{(;.,;4...,«,.),
., 11j,.
где xij - значение 1-го двоичного разряда J-й переменной,
f(xn ,xi2xin)- одна из форм функции
алгебры-логики (ФАЛ), соответствующая ПСД.
Работа устройства формирования ПСД основана на формуле
F(«,,xt,..xB)-Zl2- Z:2.(х,..кЧ1 ..,««1
Например, функция зависит от четырех аргументов и аппроксимирована совокупностью многочленов, которым соответствует полилинейная форма:
1 + 32X1X2 + 34X1X2X3X4.
Этой полилинейной форме соответствует система ФАЛ/
х,&Хг8,Х5&Х4. jX.bXfcb Cli Х4 ,
х,Ь хг Ь х,4х„, х,4 хг t , 4 х„ , x, , хД хг |.
Соответствующая этой системе ФАЛ система ПСД имеет вид
{Х1Х2ХЗХ4, 1 -Х1Х2ХЗХ4, 1 Х1Х2+Х1Х2ХЗХ4, Х1Х2, Х1Х2 - Х1Х2ХЗХ4, 1 - Х1Х2}.
В том случае, когда функция зависит от трех переменных, можно построить целую совокупность аппроксимирующих многочленов путем отождествления переменных:
1) если xi Х2 у, то полилинейная
форма имеет вид 1 + Э2У2 + Э4у
X3X4I
2)если xi хз у, то полилинейная форма имеет вид
1 + Э2УХ2 -I- 34У2Х2Х4;
3)если хз Х4 2, то полилинейная форма имеет вид
1 + 32X1X2 + Э4У Х1Х2.
Для функции, зависящей от двух переменных, имеем совокупность аппроксимирующих многочленов:
1) если xi Х2 хз у, то полилинейная форма имеет вид
1 + 32У2 + 34У Х4.
2)если Х2 хз хз у, то полилинейная форма имеет вид
1 + Э2Х1У2 + 34Х1У3.
ok,, ,0-2ia 12l2 Z2 1-- ZLz- -jji.,,.,,...,,,)
-m, ,,.,,.,
где Ф(х1, Х2,... хп) полилинейная форма.
На этом алгоритме основано вычисление значений многочлена и полиноминальной формы,
Устройство работает следующим образом.
Аргументы поступают на входы устройства и блок 1, с выходов которого на информационные входы мультиплексора поступают значения ПСД.
Вид вычисляемой функции определяется кодом, поданным на управляющие входы коммутатора, выходы которого соединены с входами сумматора 3, реализующего операцию взвешенного группового суммирования. Выходом устройства является выход сумматора 3.
На фиг. 2 приведена структурная схема устройства, реализующего вычисление
ГРУППЫ Функций -- cosx , ,х ctgx , зависящих от одного аргумента.
В случае одного аргумента.(фиг.2) аргумент подается на два входа первого умножителя 4, на выходе которого формируется
величина х , на выходе второго умножителя 4 формируется величина х . На выходе сумматора 5 имеем х - х , а на выходах первого, второго и третьего вычитателей 6 из единицы получаем соответственно 1-х ,
1-х4и1-х2+х4
Из группы функций выберем cosx. Используем предложенный алгоритм преобразования любого степенного многочлена и полилинейной формы.
где 32 -0,49670; 34 0,03705, введя дополнительное число переменных.
1)f2 x1x2:
2)f2 f6 Х1Х2 ХЗХ4 V X 1X2X3X4 V V Х1Х2ХЗХ4 V Х1Х2ХЗХ4 Х1Х2.
3)f5 Х1Х2ХЗХ4 V V
Ф 2ХЗХ4 х 1X2X3X4:
4) fa fio fia X1X2X3X4. 3. Составим системы ПСД, соответствующую этой системе ФАЛ:
Х1Х2, 1 - Х1Х2, Х1Х2 Х1Х2ХЗХ4, Х1Х2ХЗХ4.
После отождествления переменных х1 Х2 хз хз совокупность полилинейных форм примет вид
{х2. 1 - х2, jf- х4, х4}.
Код выбранной реализуемой функции cosx, поданный на управляющий вход коммутатора 2, выделяет из общей совокупности {х2. 1 - х2, 1 - х2 + х4, Xх - х4,1 - х, х4} совокупность полилинейных форм
{А 1 - х2. х2 - х4. х4}.
соответствующую реализуемой функции cosx. Она и поступает с выходов коммутатора 2 на вход сумматора 3, который осуществляет операцию взвешенного группового суммирования в соответствии с таблицей истинности для совокупности ПСД:
f 1 2° + f2
+ f5
+ fio
+ fia
+ f6.
+ f8
+
На выходе сумматора 4 получим значение реализуемой функции при представлении ее многочленом
1 + Э2Х2 + Э4Х4.
А
г
значений функций, происходит аналогичным образом.
Формула изобретения Устройство для вычисления значений группы функций, содержащее блок вычислений значений нелинейных форм двухэле10 ментного множества, отличающееся тем, что, с целью расширения функциональных возможностей за счет вычисления значений функций нескольких переменных, в негр введены коммутатор и параллельно-по1 следовательный сумматор, причем разрядный вход аргументов устройства соединен с соответствующим разрядным входом аргумента блока вычисления значений нелинейных форм двухэлементного множества, выход
20 которого соединен с информационным входом коммутатора, выход и управляющий вход которого соединены соответственно с информационным входом параллельно-последовательного сумматора и входом кода
25 функций устройства, выход которого соединен с выходом параллельно-последовательного сумматора.
ТТ..7Г
Код функции
Фиг.1
Фиг
фиг.З
| Устройство для умножения | 1984 |
|
SU1203512A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Каляев А.В Многопроцессорные системы с программируемой архитектурой | |||
| М.- Радио и связь, 1984 | |||
Авторы
Даты
1991-06-15—Публикация
1988-07-11—Подача