Нзооретение отиосится к вычислительной технике, а более конкретно к программному управлетшю технологическим оборул,ованкем.
Цель изобретения - расзпрфение области примат ения за счет вычисления скобочных форм,булевых функций, представленных в виде алг вбраических
ypfciBHBHHH .
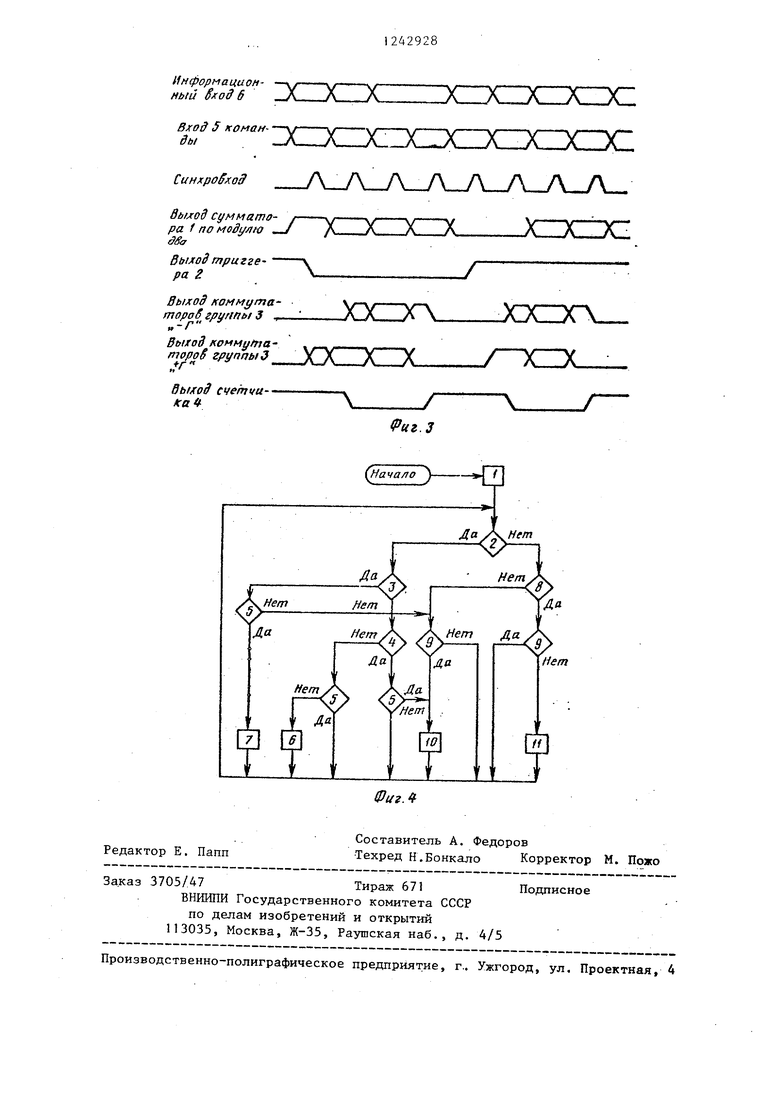
На фиг о 1 приведена структурная схема устройства для вычисления булевых функций; на фиг. 2 - цример реализации устройства на уроЕне стандартных функциональных элементов; на фиг . 3 временная диаграмма работы устройства; на фиг, 4 - алгоритм работы устройства.
Устройство (фиг., и 2) содер кит сумматор 1 по модулю два, триггер Z, группу 3 коммутаторов 5 реверсивный счетчик 4. грунпу входов 5 команды, информационный вход 6 и вьгеод 7,
Первый коммутатор группы 3 (фиг. 2) может быть выполнен в виде элемента ЗАПРЕТ 8, второй комм:утатор может быть выполнен на элементе 9 к элементе (2--4)И-2ИЛИ 10, установка устройства в исходное состояние и синхрок изация ос-уществляются по входу 1 1 з Становки в исходное COCTCSH ние и синхрозходу 12,
На фиг. 3 приведена временная диаграмма работы устройстваS где показано взаимное расположение сигналов на информационном входе б, входе 5 команды и синхровходе 12 устройства, выходах сумматора 1 по модулю два, триггера 2, ггервого и второго коммутаторов грунпы 3 к вьжода реверсивного счетчика 4 „
Счетчик 4 к триггер 2 (фиг. 3) могут переключаться 3 например по переднему фронту сзтгнала поступающего на синхровход 12 устройства, С приходом сиихронизирующегс импульса при одинаковых уровнях логических сигналов на входах обратного и прямого приращения счетчик 4 не изменит своз го состояния. Синхронизирующий импульс подггется на синхровход 1 2 устрой с тв а , когда сигналы на входах элементов устройства п рг-шиманп установившиеся значения,
Сигнал установки устройства в исходное состояние, переводяший счетчик Д в состояние О , а триггер 2 в состояпие 1 з подается асинхронно на вход 11 установки в исходное соС 1 ояние уг:т1)ойства перед каждым никлом вычисления очередной булевой функции,
На фиг, 4 представлен алгоритм раЕзоты устройства; логические блоки которого выполняют след тат;ие действия: блок 1 - установить состояние г:четчика 4 разное О и состояние триггера 2 разное Г ; блок 2 - проверить состояние счетчика 4 на равенство блох 3
проверить состоятгие триггера 2 на равенство
блок ч -- проверить;, совпадает ли действительное значение аргумента со
i- значением, указанным в уравг ении; блок 5 - про зерить, имеется ли знак ,1из ьюнкпии блок б - установить С .чостояние триггера 2 равное блок 7 - установить состояние триг ) гера 2. равное блок 8 - прове- оить, имеется ли закрывающая: скоба
),. бл1эк S - проверить, имеется ли открывающая скоба (; блок 10 - увеличить содержимое счетчика 4 на блок 1 -- уменьшить содержимое счетчика 4 на .
Ус.тройет зо использует ,для вычисления б;7левь1Х функций алгебраических 1, равмений знак дизъюнкции Ч, от крывающие ( и закрывающие ) скоб- - к и.
аргл кента, указанное в ура.внении равно I, если этот аргумент входит Е уравнение без знака
.;; инверсии, в противном оно равно О,
образоМ; результат операции ЙСКШОЧ,,Юи1ЕЕ ЯПИ равный О над сиг11;5лами Дей:ствительное зкачени ; аргумента и Значение аргумента , у1-.аза1шое в урав1-1епии свидетельствует о том,, что данный аргумент истинен, - ПРОТИ13КОМ случае он ложен.
Рассмотрит-- гтример уравнения, (Х2-1-ХЗ -Х4)и(Х5х76(Х7+Х8))х
xX9+X10 Y(1)
,Г.(, ,любогс булевого уравнения вы- Ислетшя ведут в порядке естественной записи слевгг нап оаво. С Ля уравнения (1) индексы при ар- гхвдеитах определяют порядок вычисления.
В начале вычисления устанавливают значение функции равное 1. Ре- : шают уравнение, вьг-тисляя по порядку аргут-генты,-.
В процессе вылиапепия уравнения слчцествчгют два условньпс перехода г
когда вычисленный аргумент истинен и после него стоит знак дизъюнкции +, когда вычисленный аргумент ложен и после него нет знака дизъюнкци (т.е. стоит знак конъюнкции).
В примере (уравнение ()) знак дизъюнкции стоит после аргументов Х2, ХЗ, Х5, Х7 и Х9. ,
В первом случае процедура условного перехода такова: функции присваивается значение единицы, накладывается запрет на вычисление остальных слагаемых дизъюнкции до отыскания последнего аргумента, входящего в данную дизъюнкцию, после чего вычисление продолжается.
Очевидно, если уравнение заканчивается последним членом этой дизъюнкции, то результатом решения этого уравнения будет 1.
Во втором 11.
функции присваивается значение ноль, накладываетс запрет на вычисление остальных сомножителей данной конъюнкции до отыскания последнего аргумента, обнаруживается дизъюнктивный член к этой части функции, в которую входит только что вычисленная конъюнкция, функции присваивается значение 1 и вычисление продолжается. Очевидно, что если уравнение заканчивается последним числом данной конъюнкции, то результатом решения этого уравнения будет О. Для отыскания последнего аргумента дизъюнкции при первом условном переходе рассмотрим дизъюнкцию вида
Х1+Х2+ХЗ...(2)
Если эта дизъюнкция входит в состав более сложного аргумента, то она должна быть заключена в скобки
(Х1+Х2+ХЗ. . .+х|,)хХ „ + (3) или
Х,+ 1 (XI+X2+X3+. . .+Х„)+Х„+2 (4) где Х„+1 и - любые сколь угодно сложные аргументы.
Из уравнений (3) и (4) видно, что окончание дизъюнкции определяется наличием закрывающей скобки. Однако любой член дизъюнкции может быть в свою очередь сложным аргументом и .содержать скобки. Например (В2+ +ВЗ), тогда уравнение (3) принимает вид
(Х1+В1(В2+ВЗ)+ХЗ+...X) (5) При этом по ходу вычисления, если, например, действительное значени XI равно 1 и совпадает со значени
15
20
242928
ем, указанным в уравнении, то результат операции ИСКЛЮЧАЮЩЕЕ ИЛИ над сигналами Действительное значение аргумента и Значение аргумента, 5 указанное в уравнении равен О. Это означает, что аргумент XI, являющийся членом дезъюнкции, истинен, так как XI стоит знак дизъюнкции +, то и вся дизъюнкция истинна. 10 Для продолжения вычислений необходимо найти последний член этой дизъюнкции. Однако закрывающая скобка после аргумента ВЗ не характеризует окончание данной дизъюнкции. Такие скобки, принадлежащие сложным аргументам, характеризуются тем, что каждой закрывающей скобке соответствует открывающая скобка и лишь последняя закрывающая скобка, указывающая на конец дизъюнкции, оказьгоается нескомпенсированной открывающей скобкой. Поэтому правило для отыскания последнего члена дизъюнкции можно трактовать так: по ходу вычисления подсчитьшает- ся количество открывающих и закрьшаю- щих скобок и тот наиболее близкий . щаг вычислений, в котором число закрывающих скобок хотя бы на одну больше числа открывающих скобок, указывает на конец дизъюнкции.
Для отыскания последнего аргумента конъюнкции при втором условном переходе рассмотрим конъюнкцию Х1хХ2хХЗ...X Y (6) Если эта конъюнкция входит в состав более сложного аргумента, то после нее должен стоять знак дизъюнкции, с помощью которого 1к ней присоединяется в общем случае любой, сколь угодно сложный аргумент XlxXlx xX3...X,,+X,+ (7).
Из уравнения (7) видно, что окончание конъюнкции определяется наличи25
30
35
40
ем знака дизъюнкции +. Однако как - и при первом условном переходе, каждый из аргументов может быть сколь угодно сложным, содержащим в свою очередь знак дизъюнкции и скобки.
Например Х2х(В1+В2)хХЗ...
50
(8).
Тогда перед каждым знаком дизъюнкции, входящим в сомножитель вычисляемой конъюнкции, должна быть открывающая скобка и лишь в том .случае, 55 когда все открывающие скобки скомпенсированы закрывающими, знак дизъюнкции + является указанием на окончание конъюнкции.
Тогда правило для отыскания последнего члена ко 1ъюнкт1,ии можно трактовать так: по ходу вычисления подсчитывается ко1п-1чество открываю- щих и закрывающих скобок, причем закрывающие скобки считаются лишьЕ тогда, когда имеется хотя бы одна открывающая скобка. Если разность между числом открывающих и закрыва- ющих скобок равна нулю, то наиболее близкий по ходу вычисления знак дизъюнкции + указывает на окончани конъюнкции.
Устройство работает следующим образом (фиг. 1 -4).
В начале вычислений счетчик 4 устанавливается в состояние ноль (значение его выходного сигнала равно единице), а триггер 2 - в состо яние единица. В процессе вычислени последовательно по шагам для каждого аргумент.а булевого уравнения сумматор 1 по модулю два проверяет совпадение сигналов Действительное зна- чение аргумента (на информационном входе) и Значение аргумента, указан ное в уравнении. Если-для какого- либо аргумента его действительное состояние совпадает со значением, указанным в уравнении, то на выходе сумматора 1 по модулю два появляется сигнал логический ноль. Если к тому же имеется знак дизъюнкции +, то выполняются условия для первого условного перехода и сигнал + (через второй коммутатор группы 3) увеличивает на единицу значение содержимого счетчика 4.
Когда содержимое счетчика 4 от- личается от исходного, то значение его выходного сигнала принимает состояние равное нулю, при этом накладывается запрет на вычисление последующих аргументов и изменение со- стояний триггера 2.
Начинается подсчет счетчиком 4 открьшающих и закрывающих скобок. При этом коммутаторы группы 3 функционируют таким образом, что на вход обратного приращения счетчика подается сигнал Закрывающая скоба, а на вход прямого приращения сигнал Открывающая скоба. Когда количество закрываюпсих скобок хотя бы на одн больше числа открывающих скобок, счетчик 4 устанавливается в исходное состояние О, а его выходной сигнал
принимает значение 1 , и вычисления продолжаются.
Если Для какого-либо аргумента его действительно е состояние не совпадает со значением, указанным в уравнении, то на выходе сумматора 1 по модулю два появляется сигнал логическая
II 1 П
Если отсутствует знак дизъюнкции +, то вьшолняются условия для второго условного перехода. Триггер 2 сбрасывается в состояние О, а на его выходе 7 устанавливается значение выходного сигнала (функции) равное О. Счетчик 4 подготовлен к отсчету открывающих и закрывающих скобок, причем закрывающие скобки подсчитываются лишь тогда, когда имеется хотя бы одна открывающая скобка. Если на ходу вычисления все открывающие скобки скомпенсиро1заны закрывающими (состояние счетчика 4 равно О) и имеется знак дизъюнкции +, то триггер 2 устанавливается в исходное состояние, равное 1, и вычисления продолжаются.
После проверки всех аргументов реализуемой булевой функции, представленной в виде алгебраического уравнения, значение функции О или 1 снимается с выхода 7 триггера 2. Это значение является результатом решения уравнения.
Рассмотрим в качестве примера работу ус тройства при вычислении урав нения (1). Для определенности предположим, например, что аргументы XI, ХЗ, Х7, XIО находятся в состоянии логической единицы, а остальные аргументы в состоянии логического нуля. .
Составим таблицу, характеризующую состояние устройства в процессе вычисления .
Формула изобретения
Устройство гщя вычисления буле- вьпк функций, содержащее сумматор по модулю два, триггер, группу коммутаторов и реверсивный счетчик, входы обратного и пругмого приращения и синхровход которого соединены соответственно с выходами первого и второго коммутаторов группы и синхровходом устройства, входы сумматора по модулю два соединены с информационным входом устройства и входом команды Значение аргумента, указанное в уравнении устройства, отличающееся, тем, что, с целью расширения области применения устройства за счет вычисления скобочных форм булевых функций, представленных в виде алгебраических уравнений, первый коммутатор состоит из элемента ЗАПРЕТ, второй коммутатор группы состоит из элемента НЕ-ИЛИ и элемента (2-4)И-2ИПИ, причем выход признака нуля реверсивног счетчика соединен с инверсным входом элемента ЗАПРЕТ, первым входом элемента НЕ-ИЛИ, первым прямым входом первой группы входов элемента (2-4)И-2ИЛИ, первым входом первой .грзшпы входов установки единицы и
первым прямым входом группы входов установки нуля триггера, второй вход первой группы входов установки единицы и инверсный вход группы входов установки нуля которого соединен с вхо- номер условного перехода. Вьтисленное значение функции в данном случае равно единице.
дом команды Дизъюнкция устройства и вторым прямым входом первой группь. входов элемента (2-А)И-2ИЛИ, третий 5 прямой вход первой группы входов
которого соединен с выходом триггера, .выходом устройства и вторым входом элемента НЕ-ИЛИ, выход которого соединен с первым входом второй группы
0 входов элемента (2-А)И-2ИЛИ, второй вход второй группы входов которого соединен с входом команды Открывающая скоба устройства, вход команды Закрывающая скоба которого соеди5 нен с прямым входом элемента ЗАПРЕТ, инверсный вход первой группы входов элемента (2-4)И-2ИЛИ соединен с, выходом сумматора по модулю два и вторым прямым входом группы входов усга0 новки нуля триггера, синхровход и вход начальной установки которого соединены соответственно с синхро- входом и входом установки в исходное состояние устройства, вход сброса
5 реверсивного счетчика соединен с входом установки в исходное состояние устройства.



| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для вычисления булевых функций | 1984 |
|
SU1218376A2 |
| Устройство для вычисления булевых функций | 1986 |
|
SU1372319A1 |
| Устройство для вычисления булевых функций | 1982 |
|
SU1049898A1 |
| Устройство для вычисления булевых функций | 1984 |
|
SU1254462A1 |
| Устройство для моделирования конечных автоматов | 1980 |
|
SU955080A1 |
| Устройство для подсчета числа ответвлений диаграммы | 1983 |
|
SU1160391A1 |
| Устройство для определения значений булевых функций | 1990 |
|
SU1805462A1 |
| Устройство для моделирования конечных автоматов | 1977 |
|
SU717775A1 |
| Устройство для вычисления булевых функций | 1986 |
|
SU1332310A1 |
| Устройство для определения значений булевых функций | 1987 |
|
SU1508204A1 |

Изобретение относится к вычислительной технике и предназначено для вычисления булевых функций, представленных в виде алгебраических уравнений. Цель изобретения - расширение области применения устройства за счет вычисления скобочных форм булевых функций, представленных в виде алгебраических уравнений. Устройство содержит сумматор по модулю два, триггер, группу коммутаторов, реверсивный счетчик. На входы команды устройства подаются сигналы Значение аргумента, указанное в уравнении, Дизъюнкция, Открывающая скоба и Закрывающая скоба. На информационный вход устройства подаются действительные значения аргументов уравнения. Вычисление булевого уравнения ведется в порядке естественной записи аргументов. После вычисления последнего аргумента полученное значение функции считывается с выхода тригге ра. 4 ил. , 1 табл. W tc iU N5 50, CN
о
hT
Фиг. 1
5 ЗaкpыSaюuцaf скобка Oj
CJ Откры Satoui, afl
j. скобка О--
i Дизъюнк- Q,
Значение л
«ааргумен- Oi
чта,иказан«JQное 6 уравнении
8
&
/г
0
с
5Я
Ч
™.
ч
Ин(рорма 4и онный $;(од iS
тг
Устаноёка // § исходное о™- состояние
-.-о Втход
Инфор ацион- ныи Sfod 6
Вход 5 команды
DdXIDC
.X A-ZlA AZ-IXZ.
--vуw-уууууу -Л / лЛ -«..ухАЛи-,
..
X Л Д Д
JOCDTX
у
.X A-ZlA AZ-IXZ.
У
у
iPuz.S
(Начало fiem
Редактор E. Папп
Заказ 3705/47Тираж 671
ВИНИЛИ Государственного комитета СССР
по делам изобретений и открытий 113035, Москва, Ж-35, Раушская наб., д. 4/5
Производственно-полиграфическое предприятие, г.. Ужгород, ул. Проектная, 4
ФигЛ
Составитель A. Федоров
Техред Н.Бонкало Корректор М. Пожо
Подписное
| Устройство для вычисления булевых функций | 1975 |
|
SU610104A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Устройство для вычисления булевых функций | 1982 |
|
SU1049898A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Устройство для подсчета числа ответвлений диаграммы | 1983 |
|
SU1160391A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1986-07-07—Публикация
1984-09-04—Подача