Ё

| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой функциональный генератор | 1987 |
|
SU1425631A1 |
| Цифровой функциональный генератор | 1988 |
|
SU1566333A1 |
| МНОГОКАНАЛЬНАЯ СИСТЕМА ДЛЯ СЕЙСМИЧЕСКИХ ИССЛЕДОВАНИЙ | 2020 |
|
RU2722462C1 |
| Генератор ортогональных сигналов | 1982 |
|
SU1073766A1 |
| ГЕНЕРАТОР ПОСЛЕДОВАТЕЛЬНОСТЕЙ КОДА СТИФФЛЕРА | 2017 |
|
RU2668742C1 |
| Генератор функций Попенко-Турко | 1990 |
|
SU1753464A1 |
| ГЕНЕРАТОР ТРАНСОРТОГОНАЛЬНЫХ КОДОВ | 2000 |
|
RU2200972C2 |
| ГЕНЕРАТОР КВАЗИОРТОГОНАЛЬНО-ПРОТИВОПОЛОЖНЫХ СИГНАЛОВ | 1999 |
|
RU2187144C2 |
| Генератор квазиортогональных сигналов | 1989 |
|
SU1755270A1 |
| Функциональный преобразователь | 1978 |
|
SU813449A1 |
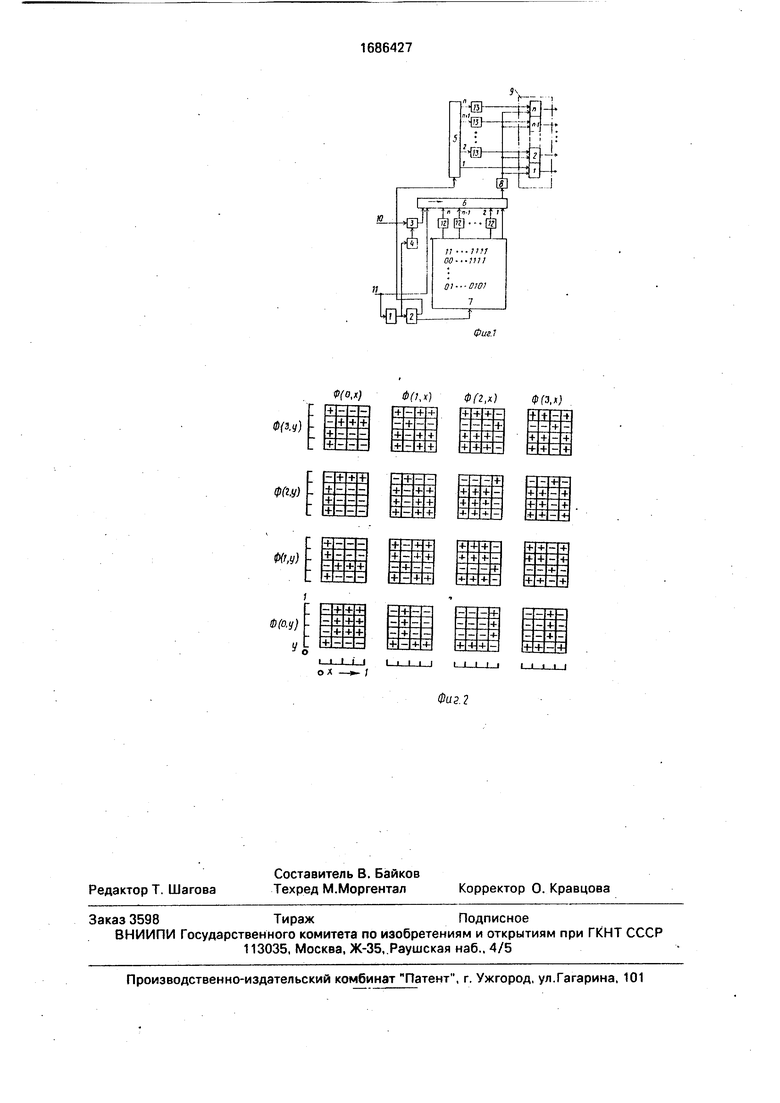
Изобретение относится к автоматике и вычислительной технике и может быть использовано для обработки двумерных сигналов и изображений, а также в системах спектрального анализа и информационно-измерительных комплексах. Цель изобретения - расширение функциональных возможностей генератора за счет генерирования системы ортогональных функций с малой эффективной шириной спектра Цифровой функциональный генератор содержит счетчики 1, 2, элемент ИЛИ 3, элемент задержки 4, блок 5 формирования функций Уолша, регистр сдвига 6, блок 7 памяти, элемент НЕ 8, сумматоры по модулю два 9, группы элементов НЕ 12, 13. Две груплы элементов НЕ позволяют преобразовать систему ортогональных функций в систему с меньшей эффективной шириной спектра. 2 ил.
Изобретение относится к автоматике и вычислительной технике и может быть использовано для обработки двумерных сигналов и изображений, а также в системах спектрального анализа и информационно- измерительных комплексах.
Цель изобретения - расширение функциональных возможностей генератора за счет генерирования системы ортогональных функций с малой эффективной шириной спектра.
На фиг. 1 представлена структурная схема генератора; на фиг. 2 - первые шестнадцать дискретных ортогональных функций от двух переменных.
Генератор содержит счетчики 1 и 2, элемент ИЛИ 3, элемент 4 задержки, блок 5 формирования функций Уолша, регистр б сдвига, блок 7 памяти, элемент НЕ 8, сумматоры по модулю два 9, вход 10 начальной установки, тактовый вход 11, группы элементов НЕ 12 и 13. Система двумерных дискретных ортогональных функций, формируемых генератором, определяется следующим образом:
Ф(к,т,х,у) Ф (к,х)8 Ф(т,у), где Ф (k,x) - вектор-строка;
Ф (т,у) - вектор-столбец;
8 кронекеровское произведение.
Одномерные функции Ф (k,x) и Ф(т,у) формируются из одномерных функций Уолша Wal(k,x) и Wal(m,y) посредством инвертирования четных элементов первой половины периода и всех элементов второй половины периода соответствующей одномерной функции Уолша.
Например, при N 4 система функций Уолша имеет вид
С
00
а
4 Ю VI
1111 111 1 1 -1 -1 -1 1 -1 1 -1
(1)
После инвертирования элементов получим новую систему ортогональных функций
Ф
Двумерная функция, например, Ф(3,2,х,у) вычисляется следующим образом. Ф(3,2,х,у) Ф(3.х)®Ф(2,у)1 -1 1
1 1 1
-1
11-11
11-11
11-11
1-1 1 -1
Система N двумерных функций показана на фиг. 2.
Двумерные дискретные ортогональные функции, формируемые предлагаемым генератором, имеют эффективную ширину спектра, меньшую, чем функции Уолша. В блоке 7 памяти в виде матрицы (1) записана система функций Wal(k.x). Столбцы аналогичной матрицы Wal(m,у) последовательно формируются блоком 5 формирования функций Уолша. Преобразование функций Уолша в функции Ф(к,х) и Ф(т.у) осуществляется при помощи элементов НЕ 12 и 13, а кронекеровское умножение функций - при помощи элемента НЕ 8 и сумматоров по модулю два 9. Строка Ф(к,х) переписывается параллельным кодом в регистр 6 сдвига, а на вход элемента НЕ 8 подается с регистра сдвига в последовательном коде. Счетчик 1 отсчитывает N тактовых импульсов, поступающих с входа 11 генератора на сдвигающий вход регистра б сдвига и необходимых для выдачи последовательного кода. По сигналу переполнения счетчика 1 в регистр 6 сдвига из блока 7 памяти записывается очередная строка матрицы (или по управляющему сигналу на входе 10 в начале работы генератора). При этом в счетчике 2 формируется очередной адрес номер строки матрицы. Элемент 4 задержки обеспечивает временное согласование работы блоков. После перебора всех строк по импульсу переполнения счетчика 2 производится выдача очередного вектора-столбца Wal(m,y) на выходы блока 5, и далее цикл повторяется. Формула изобретения Цифровой функциональный генератор,
содержащий два счетчика, блок памяти, блок формирования функций Уолша, регистр сдвига, п сумматоров по модулю два п - размерность системы генерируемых функций), элемент задержки, элемент ИЛИ, элемент
5 НЕ, причем вход первого счетчика является тактовым входом генератора и соединен со сдвигающим входом регистра сдвига, выход переполнения первого счетчика соединен с входом- второго счетчика и через элемент
0 задержки - с первым входом элемента ИЛИ, информационный выход и выход переполнения второго счетчика соединены соответственно с адресным входом блока памяти и синхронизирующим входом блока формиро5 вания функций Уолша, (21 - 1Уй разрядный выход блока памяти (I 1,п/4) соединен с соответствующим информационным разрядным входом регистра сдвига, последовательный выход регистра сдвига через
0 элемент НЕ соединен с первыми входами всех сумматоров по модулю два, (21 - 1)-й выход блока формирования функций Уолша соединен с вторым входом соответствующего сумматора по модулю два, выходы суммэ5 торов по модулю два являются выходами генератора, второй вход элемента ИЛИ является входом начальной установки генератора, выход элемента ИЛИ соединен с управляющим входом записи регистра
0 сдвига, отличающийся тем, что, с целью расширения функциональных возможностей генератора за счет генерирования системы ортогональных функций с малой эффективной шириной спектра, он содер5 жит две группы по Зп/4 элементов НЕ, причем 21-й и п/2 + )-й разрядные выходы блока памяти 0 1 ,п/2) через 1-й и j-й элементы НЕ первой группы соответственно соединены с 21-м и (п/2 + )-м информа0 ционными разрядными входами регистра сдвига, 21-й и (п/2 + j)-u выходы блока формирования функций Уолша через 1-й и J-й элементы второй группы соответственно соединены с вторыми входами 215 го и (п/2 + j)-ro сумматоров по модулю два.
(о,}
Ф(зч)
$(,) Ф(г,х) ф(э,)
| Генератор дискретных ортогональных функций | 1986 |
|
SU1386981A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Цифровой функциональный генератор | 1987 |
|
SU1425631A1 |
| кл | |||
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1991-10-23—Публикация
1989-09-11—Подача