Изобретение относится к области управления ядерными энергетическими реакторами и может быть использовано при выводе на мощность энергетических реакторов, критических сборок, космических ЯЭУ, а также в системах аварийной защиты реакторов и критических сборок.
Целью изобретения является разработка способа идентификации периода разгона, удовлетворяющего условиям надежности (под надежностью понимается недопустимость выдачи значения периода разгона, меньшего или равного заданному, раньше, чем оно в действительности реализуется) и безопасности (при достижении заданного периода оценка по предлагаемому способу не должна быть завышенной), а также существенное увеличение точности идентификации заданного значения периода разгона и отказ от резервирования измерительной аппаратуры. Изобретение поясняется фиг. 1-3.
Сущность способа состоит в том, что период разгона определяется в приближении квазистатического изменения мощности N реактора, описываемого элементарным уравнением кинетики, откуда период разгона реактора в момент времени t равен
t = N/(dN/dt). (1)
Введена новая операция по получению экспериментальной зависимости числа импульсов детектора за интервал времени Δt от времени Ni(ti)(i = 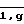 ), где g - число элементов в группе, составляющих экспериментальную зависимость, на интервале времени
), где g - число элементов в группе, составляющих экспериментальную зависимость, на интервале времени 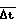 = (g-1)Δ t. Интервал накопления числа импульсов детектора нейтронов связывается с заданным значением периода разгона τо соотношением и устанавливается равным
= (g-1)Δ t. Интервал накопления числа импульсов детектора нейтронов связывается с заданным значением периода разгона τо соотношением и устанавливается равным
Δt≈ 2˙ 5 τo/(g-1) . (2)
Вычисление периода разгона производится на основе метода наименьшего направленного расхождения, который позволяет учесть априорную информацию о характере процесса и тем самым существенно повысить точность идентификации заданного значения периода разгона реактора. Способ дает возможность полностью исключить применение аналоговой техники.
Вычислительная процедура по определению значения периода разгона в этом случае выглядит следующим образом.
Записываются в память ЭВМ компоненты матрицы
ai,j= exp(ti/τj) (i= 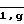 ; j=
; j= 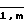 ) (3)
) (3)
(τi≈0,9τ0; τj+1= 3ij)
После получения g-го измеренного значения скорости счета детектора Ng выполняется аппроксимация группы (N1, N2, . . . Ng), для определения коэффициентов хj в уравнении
N(t)= 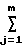 exp(t/τj) . (4)
exp(t/τj) . (4)
Полагается
X1(o) = X2(o)= X3(o) = X4(o) = 1.
Выполняется 100 итераций по рекуррентной формуле
X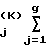 a
a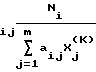 . (5)
. (5)
Рассчитывается значение  в последней (g-й) точке группы
в последней (g-й) точке группы =
= 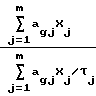 (j=
(j=  , m) . (6)
, m) . (6)
С получением нового измеренного значения Ng+1 из аппроксимируемой группы исключается значение N1, заменяются индексы оставшихся Ni+1_→ Ni и добавляются в группу Ng+1_→ Ng.
Положительный эффект при осуществлении способа достигается за счет того, что способ алгоритмически ориентирован на идентификацию с высокой точностью только одного заданного значения периода разгона реактора. Остальные значения разгона идентифицируются с меньшей точностью, но достаточной для того, чтобы гарантированно выполнялись условия надежности и безопасности. Высокая точность и надежность алгоритмической реализации способа обусловлена вычислением производной dN/dt в выражении для периода (1) по аналитической зависимости, аппроксимирующей экспериментальную зависимость Ni(ti) на интервале времени 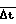 = (g-1) Δt.
= (g-1) Δt.
Аппроксимация осуществляется по методу наименьшего направленного расхождения суперпозицией экспонент, периоды которых задаются из условия, чтобы они в совокупности дискретно охватывали весь предполагаемый диапазон измерения периода разгона реактора. В процессе аппроксимации при подборе весовых коэффициентов при экспонентах с заданными периодами МНРН позволяет учесть априорную информацию о процессе (монотонность функции изменения нейтронной мощности) и тем самым повысить точность аппроксимации экспериментальной зависимости Ni(ti), а следовательно, и точность определения периода разгона.
Для обеспечения приемлемого числа итераций, позволяющего проводить идентификацию в режиме реального времени (до получения следующего измеренного значения числа импульсов детектора), и для создания условия корректности идентификации заданного значения периода разгона интервал аппроксимации 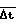 связывается с заданным значением периода разгона τо соотношением
связывается с заданным значением периода разгона τо соотношением 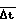 = (g-1)Δt ≈ 2˙5τо. Отсюда для временного интервала набора импульсов детектора должно выполняться условие
= (g-1)Δt ≈ 2˙5τо. Отсюда для временного интервала набора импульсов детектора должно выполняться условие 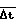 ≈ 2˙5τо/(g-1).
≈ 2˙5τо/(g-1).
Данный способ идентификации заданного значения периода разгона проявляет слабую чувствительность к виду детектора нейтронов, поскольку оценка периода разгона делается по гладкой кривой, построенной по ММРН с учетом априорной информации. Это позволяет отказаться от резервирования измерительных каналов и использования в них различных детекторов нейтронов в различных диапазонах изменения нейтронной мощности. Аппаратная реализация способа идентификации базируется полностью на микросхемах, что позволяет избавиться от погрешности в идентификации периода разгона, обусловленной нелинейностью и дрейфом характеристик решающих элементов аналоговой техники.
С целью апробации данного способа идентификации заданного значения периода разгона на критической сборке БФС-40, моделирующей быстрый реактор с замедляющим отражателем, было проведено шесть экспериментов по идентификации минимального значения периода разгона. Описание переходных процессов в этой сборке с погрешностью не более нескольких процентов справедливо в рамках точечной кинетики. Сценарий экспериментов был принят следующим: из критической сборки, содержащей источник нейтронов, выводятся последовательно с постоянными скоростями VА31, VА32, VAp группы органов АЗ1, АЗ2, АР. Последним с постоянной же скоростью vкс выводится орган КС, обеспечивающий выход критической сборки в состояние надкритичности на запаздывающих нейтронах. Сборка выдерживается в таком состоянии до выхода на физический уровень мощности ≈6 Вт с установившимся периодом разгона ≈222 с.
Измерение нейтронной плотности в экспериментах проводилось с помощью импульсного детектора СНМ-18 и токовой ионизационной камеры КНК-56 с последующим преобразованием величины тока в частоту стандартных импульсов. Начальная статистика за интервал накопления составляла в токовом канале ≈50, в импульсном ≈100 импульсов. В качестве заданного значения периода разгона τо, которое необходимо идентифицировать, максимально точно, предполагалось рассматривать минимальный в каждом эксперименте период разгона. Для численного моделирования такого эксперимента необходимы следующие параметры критической сборки: характеристики и веса всех органов регулирования (получены на экспериментах по индивидуальному взвешиванию органов); нейтронно-физические характеристики сборки, необходимые для моделирования динамики (получены из расчетов по методу Монте-Карло и составляет βэф = 0,007, l = 1,6˙ 10-6 (время жизни нейтронов); кинетические параметры для источников запаздывающих нейтронов (применимы данные Кипина для деления 235U быстрыми нейтронами).
Чтобы иметь возможность оценить точность идентификации минимального периода разгона по группе g экспериментальных данных, необходимо знать истинное значение идентифицируемого параметра. Точно определить период разгона с помощью имеющегося периодомера в процессе экспериментов оказалось невозможным. В такой ситуации (когда нет информации об истинных текущих значениях периода разгона) максимально точную оценку периода разгона в некоторый момент времени t можно получить по кривой, аппроксимирующей экспериментальные данные всего процесса. Для этого по результатам каждого эксперимента (под отдельным экспериментом понимается эксперимент, проводимый по сценарию, изложенному выше) решалась задача двухпараметрической безусловной минимизации функционала невязки σ2 - суммы квадратов отклонений измеренных значений скорости счета от соответствующих значений скорости счета, принадлежащих аппроксимирующей кривой
σ2(No, vкс) _→ min
No∈S1 (7)
vкс∈S2, здесь No - начальная скорость счета детектора;
vкс - скорость вывода органа КС.
Области изменения параметров S1 и S2 задаются в окрестностях известных с погрешностью значений No и vкс.
Связь σ2 с No и vкс - алгоритмическая. Минимизация функционала σ2 (No, vкс) осуществляется методом покоординатного спуска. Для расчета функционала невязки использовалась математическая модель эксперимента на основе "точечных" уравнений нейтронной кинетики.
Уравнение математической модели эксперимента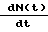 =
= 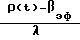 N(t)+
N(t)+ 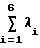 Ci(t)+q(t) ;
Ci(t)+q(t) ;
I= (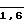 )
)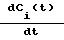 =
= 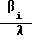 N(t)-λiCi(t) . (8) здесь q(t) - интенсивность эффективного источника нейтронов, остальные обозначения - общепринятые. Выражение для реактивности ρ (t), входящей в систему (8), определено следующим образом: ρ(t) = ρo + ρAЗ1 + ρАЗ2 + ρАР + ρКС, (9) где ρо - реактивность сборки в момент t = 0 (получена по известному, установившемуся в конце эксперимента периоду разгона и известным весам органов регулирования).
N(t)-λiCi(t) . (8) здесь q(t) - интенсивность эффективного источника нейтронов, остальные обозначения - общепринятые. Выражение для реактивности ρ (t), входящей в систему (8), определено следующим образом: ρ(t) = ρo + ρAЗ1 + ρАЗ2 + ρАР + ρКС, (9) где ρо - реактивность сборки в момент t = 0 (получена по известному, установившемуся в конце эксперимента периоду разгона и известным весам органов регулирования).
ρАЗ1, ρАЗ2, ρКС - реактивность, вводимая органами АЗ1, АЗ2, АР и КС соответственно (определена известными характеристиками и весами соответствующих органов регулирования).
Интенсивность источника q(t) в уравнениях (8) определяется по известным ρo и No: q= 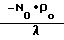 . (10)
. (10)
Для решения системы уравнений нейтронной кинетики использован специализированный алгоритм, построенный на основе численных методов Гира, позволяющих изменять величину шага интегрирования в процессе счета в широких пределах. В качестве параметров, минимизирующих функционал σ2, используется только два No и vкс из многих возможных: ρА311, ρАЗ21, ρАР, ρКС1(веса органов регулирования), vА31, vА32, vAP, vкс (скорости вывода органов регулирования), No (начальная скорость счета детектора нейтронов). Это связано с тем, что функционал σ2 максимально чувствителен к No из всех перечисленных выше параметров на всем временном интервале изменения скорости счета детектора, а к vкс - на участке вывода органа КС, где осуществляется идентификация минимального периода разгона реактора. Области изменения параметров S1 и S2 задаются в окрестностях известных с погрешностью значений No и vкс.
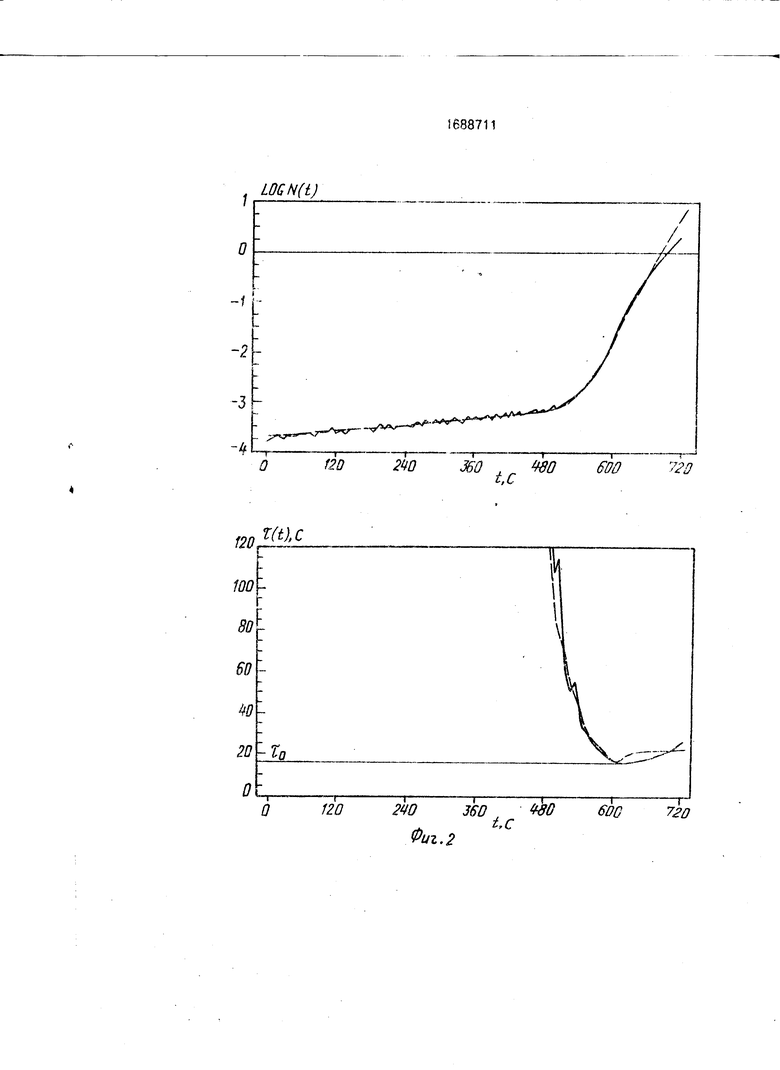
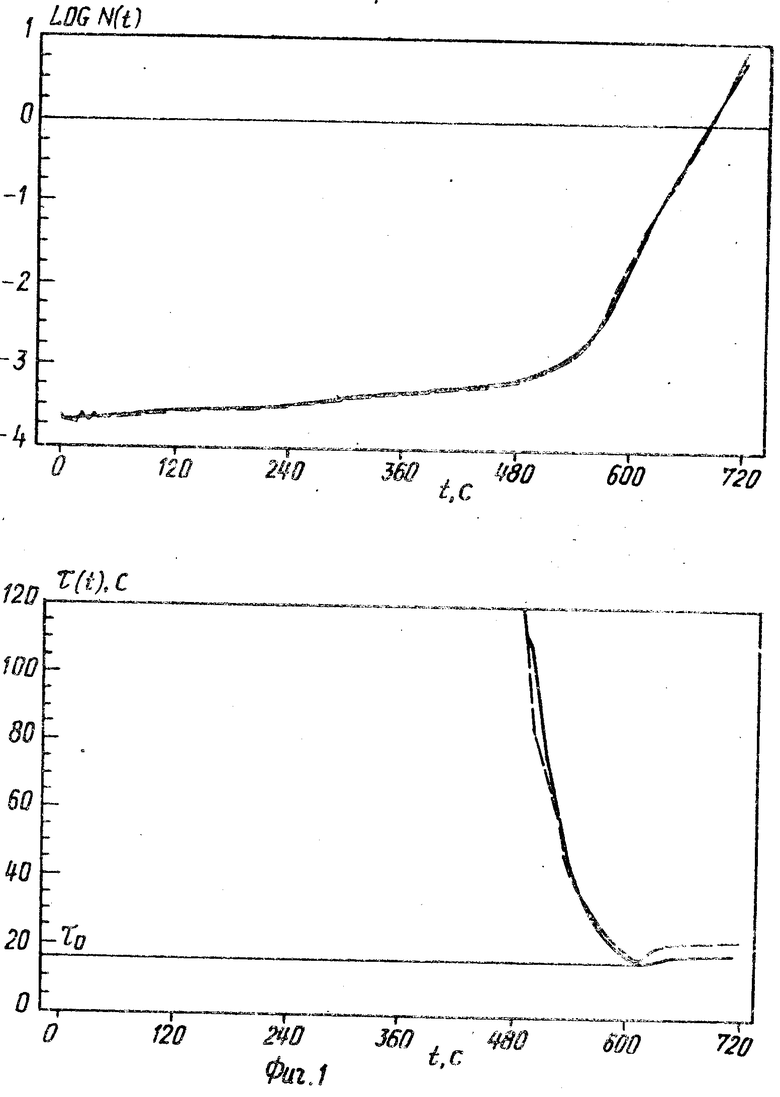
В результате минимизации невязки σ2 в пространстве параметров No и vкс для каждой экспериментальной кривой разгона получена аппроксимирующая кривая и соответствующая ей τист(t), по которой затем оценивается точность идентификации минимального периода разгона реактора. Характерный вид этих функций (пунктирная линия) показан для такового измерительного канала на фиг. 1, для импульсного измерительного канала - на фиг. 2. Обработка данных выполнена после экспериментов, но при этом имитировался режим реального времени, т. е. идентификация параметров в точке t проводилась по короткой группе данных слева от этой точки. Для этого решалась задача on-line идентификации в следующей постановке.
По информации, заданной двумя группами данных { ti} и { Ni} (i = 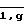 ; где g - длина группы) и представляющего собой значения времени и скорости счета детектора в критической сборке в эти моменты времени, требуется оценить период разгона и реактивность на моменты времени tg. Выполнить эту процедуру необходимо за время ≅Δt, т. е. до получения очередного измеренного значения. Длина группы задается равной g.
; где g - длина группы) и представляющего собой значения времени и скорости счета детектора в критической сборке в эти моменты времени, требуется оценить период разгона и реактивность на моменты времени tg. Выполнить эту процедуру необходимо за время ≅Δt, т. е. до получения очередного измеренного значения. Длина группы задается равной g.
Ниже приводится решение задачи оn- line идентификации по экспериментальным данным в приведенной выше постановке и даются рекомендации по настройке алгоритма идентификации заданного значения периода разгона и текущего значения реактивности. Первоначально данные каждого из шести экспериментов с токовым и импульсным измерительными каналами аппроксимировались по методике, изложенной выше. В результате были получены зависимости N(t), τ(t) для каждого эксперимента. Для первого эксперимента эти зависимости пунктирными линиями представлены на фиг. 1. 2. Зависимости τ(t) , полученные таким образом, с хорошей точностью описывают истинное поведение периода разгона в процессе эксперимента. Относительно этих зависимостей оценивалась точность идентификации периода разгона по предлагаемому способу.
В результате аппроксимации всех экспериментальных кривых истинное значение минимального периода разгона получено равным 16,08±0,08. В соответствии с ним периоды экспонент в аппроксимирующей функции (6) заданы следующими: τ1 = 15 с; τ2 = 45с; τ3 = 135 с; τ4 = 405 с (m = 4). Оптимальным размером группы измеренных значений числа импульсов детектора, по которой делается оценка периода разгона, при наблюдавшейся при экспериментальной апробации начальной статистике N1≈50-100 импульсов за интервал накопления Δt является g = 8. При g < 8 велика дисперсия восстановленного периода, при g > 8 уменьшается чувствительность способа к вновь полученному измеренному значению Ni.
Временной интервал накопления числа импульсов детектора был рассчитан в соответствии с предполагаемым τо ≈16 с по формулам (4): Δt = 6 с. Идентификация проводилась по формулам (7), (8). Погрешность идентификации минимального периода разгона по результатам всех экспериментов получена ≅ 2% как для токового, так и для импульсного каналов. Затраты времени на идентификацию одного значения периода разгона составляют ≅ 0,2 с на персональном компьютере с процессором серии 1NTEL 80286.
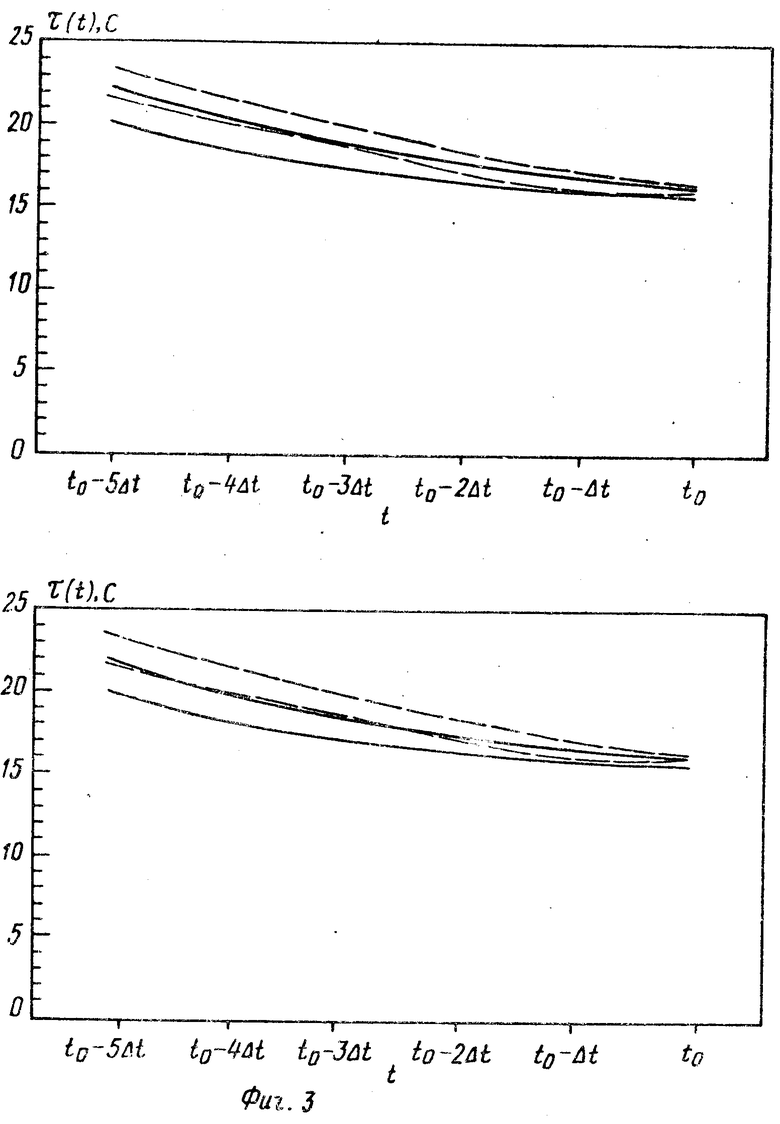
Для качественной иллюстрации результатов идентификации на фиг. 3 приведены коридоры истинных значений периода разгона на временном интервале [to - 30; to)] , где to - момент реализации минимального периода разгона, и коридор восстановленных значений периода разгона по методу наименьшего направленного расхождения. Результаты идентификации удовлетворяют условиям надежности и безопасности: обеспечено отсутствие преждевременной выдачи значения периода разгона, меньше или равного заданного; коридор идентифицированных значений периода разгона всюду ниже коридора истинных значений периода разгона, что обеспечивает невозможность выхода на такие значения периода разгона, при которых реактор оказывается неуправляемым.
Данный способ имеет следующие преимущества.
Ввиду гарантированного обеспечения условий надежности и безопасности способ позволяет исключить резервирование измерительной аппаратуры.
Предлагаемый способ идентификации периода разгона допускает аппаратную реализацию полностью на микросхемах, что позволяет избавиться от погрешности в идентификации периода разгона, обусловленной нелинейностью и дрейфом характеристик решающих элементов аналоговой техники.
Способ обеспечивает возможность выхода с большой точностью на малые значения периода разгона детектора, что повышает эффективность управления реактором по периоду (обеспечивается возможность быстрого ввода реактивности и останова органов регулирования при заданном значении периода разгона).
При использовании предлагаемого способа идентификации периода разгона в системе АЗ отпадает необходимость задания временного интервала, в котором осуществляется проверка на достоверность поступившего от токового периодомера сигнала о значении периода разгона, или появляется возможность уменьшения существующей в настоящее время инерционности аппаратуры аварийной защиты. (56) Королев В. В. , Матусевич Е. С. Системы управления и защиты критических стендов. М. : Энергоатомиздат, 1985, с. 63, 73.
Авторское свидетельство СССР N 232398, кл. С 21 С 17/14, 1968.
Изобретение относится к области управления ядерными энергетическими реакторами и может быть использовано при выводе на мощность энергетических реакторов, критических сборок, космических ЯЭУ, а также в системах аварийной защиты реакторов и критических сборок. Целью изобретения является идентификация с малой погрешностью заданного значения периода разгона реактора τo в режиме реального времени. Изобретение заключается в установке рассчитанной заранее и зависимой от τo ширины каналы временного анализатора Δt измерении зависимости числа импульсов от датчика нейтронов за интервал времени Δt на временном промежутке Δt зависящем от τo и рассчитанном заранее от времени, в вычислении по формулам на основе метода наименьшего направленного расхождения значения периода разгона реактора. 3 ил.
СПОСОБ ИДЕНТИФИКАЦИИ ЗАДАННОГО ЗНАЧЕНИЯ ПЕРИОДА РАЗГОНА РЕАКТОРА В РЕЖИМЕ РЕАЛЬНОГО ВРЕМЕНИ, включающий измерение числа импульсов N от датчика нейтронов и использование его в последующей математической обработке, отличающийся тем, что, с целью увеличения точности определения заданного значения периода разгона τ0 , в зависимости от заданного значения периода разгона τ0 устанавливают ширину канала временного анализатора Δt , определяемую по формуле Δt≈2·5τ0/(g-1) где g - количество измеренных значений N, необходимое для получения оценки периода разгона, выбираемое от интервала 5 ≅ g ≅ 15 в зависимости от величины начального статистического разброса, измеряют зависимость N1(t1)(1 =  ), числа импульсов детектора нейтронов за время Δt , пропорционального мощности реактора, от времени на интервале Δt- = (g - 1)Δt , вычисляют веса эталонных экспонент ai,j = exp(t1 / τj ) для аппроксимации зависимости Ni(ti) по формуле
), числа импульсов детектора нейтронов за время Δt , пропорционального мощности реактора, от времени на интервале Δt- = (g - 1)Δt , вычисляют веса эталонных экспонент ai,j = exp(t1 / τj ) для аппроксимации зависимости Ni(ti) по формуле
X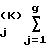 a
a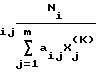
(j= 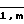 )
)
где m - количество эталонных экспонент, рассчитывают значение периода разгона по формуле =
= 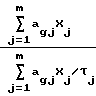 (j=
(j=  , m)
, m)
Авторы
Даты
1994-02-28—Публикация
1989-04-03—Подача