Изобретение относится к электроизмерительной технике и может использоваться для измерения разности фаз между синусоидальными сигналами и между первыми гармониками периодических сигналов в диапазоне от инфранизких до высоких частот.
Цель изобретения - повышение точности измерения.
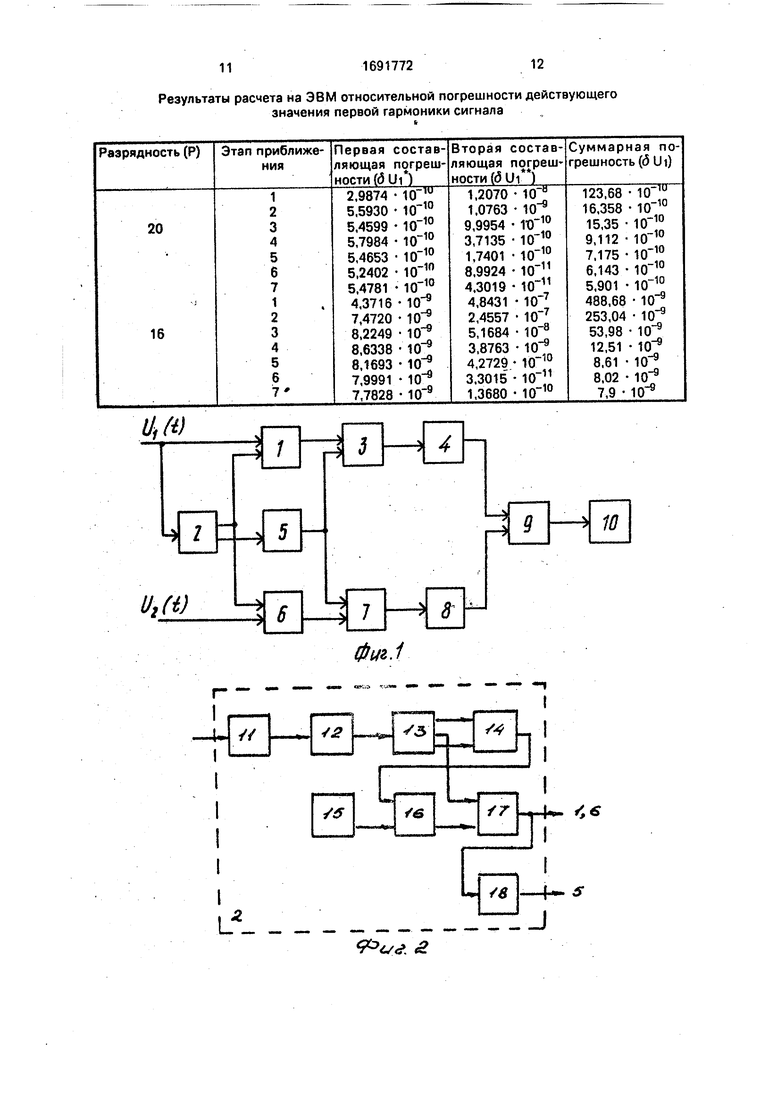
На фиг.1 представлена функциональная схема устройства, реализующего способ; на фиг.2 - схема его управления.
Устройство содержит преобразователь 1 аналог - код, первый вход которого соединен с шиной первого входного сигнала и входом блока 2 управления, выход которого соединен с вторым входом преобразователя 1 аналог - код, выход которого через вычислитель 3 коэффициентов Фурье соединен с входом вычислителя 4 фазы сигнала. Второй вход вычислителя 3 коэффициентов Фурье соединен с выходом блока 5 памяти, вход которого соединен с вторым выходом блока 2 управления. Шина второго входного сигнала соединена с первым входом преобразователя 5 аналог - код, вторым входом соединенного с выходом блока 2 управления, а выходом черезгпоследовательно соединенные вычислитель 7 коэффициентов Фурье, второй вход которого соединен с выходом блока 5 памяти, и вычислитель 8 фазы сигнала - с входом вычислителя 9 разности фаз, второй вход которого соединен с
Os
ю
VI
VI
ю
выходом вычислителя 4 фазы сигнала, а выход- с входом блока 10 индикации.
Блок 2 управления содержит последовательно соединенные формирователь 11 импульсов, счетчик 12, дешифратор 13 и триггер 14, а также последовательно соединенные генератор 15 сигналов эталонной частоты, элемент И 16, умножитель 17 частоты и счетчик 18 адреса, при этом второй вход элемента И 16 соединен с выходом триггенра 14, а второй вход умножителя 17 частоты соединен с выходом дешифратора 13.
В способе определения разности фаз измеряют коэффициенты Фурье основных гармоник двух сигналов с помощью квазисинусоидальной ступенчатой функции. Параметры ступенек квазисинусоидальной функции в точках дискретизации определяются из условия обеспечения минимальной погрешности измерения разности фаз. При этом по параметрам квазисинусоидальной функции в точках дискретизации ti и по результатам измерения мгновенных значений сигналов в тех же точках u(ti) вычисляются коэффициенты Фурье первых гармоник двух входных сигналов ui(t) и U2(t), а по ним вычисляются начальные фазы и tyi и разность фаз
Ґ 1--$2.
Выбор параметров ступенек дискретизации основан на следующем.
Пусть Ci, 6i и Si, Si - точные и приближенные значения косинуса и синуса в отдельных дискретных точках периода. Запишем формулы для точных и приближенных значений квадрата действующего значения первой гармоники сигнала:
±ШЬ,с,)г +
I vnl 1 I
(2
Ml
uiSi
}
,-v if/on «, 2 /on 2
°4 U«aMUwS
(1)
Легко видеть, что в формулах (1) вместо точных значений косинуса и синуса используются их приближенные значения Ci и Si.
Определим линейные приближения для погрешностей, которые получаются при указанной замене:
Ј-Ј{№«)
Ч1И1Ь е (
dU2 с
fcz
2|,Ј,
uiSi
У,1-
(3)
Используя выражения (2) и (3), можно записать
AiV-S AC.+ ,- i , dCii Э5|
on
-; 2 (ai ACi + bi ASi)ui,(4)
где ai.bi - коэффициенты Фурье.
Введем обозначение
Vi ui- aicosti+ bisinti -Uo,(5)
где ui - мгновенные значения сигнала в точках;
Uo- постоянная составляющая сигнала.
Точные значения синуса и косинуса распределены по периоду следующим образом: для синуса
Si, SzSn/4, Sn/4-1, ... Si,0,
- Si, - 82- Sn/4, - Sn/4-1, ... - Si, 0;
(6) для косинуса
Sn/4, Sn/4-1, ... , Si, 0, Si- Sn/4,
- Sn/4-1- Si, 0, SiSn/4.(7)
Аналогичные последовательности будут для приближенных значений синуса и косинуса и для их погрешностей. На основании формул (6) и (7) можно
показать справедливость соотношений
2 ACi %
1i 1
J ACiSi Ј ASiSi;
- ii - л
™ Ii - j
ACiS, Ј ASiCi-0; (8)
1i 1
iAC,2 SASi2;
1i 1
Ј AC(.
i 1
55 На основании формул (5)-(7) соотношение (4) можно записать в виде
§ AS,Si +
л- 2 4
п
+ | § (ai ACi+biASi)Vi (9) л, -,
Используя неравенство Коши, получим
±
1 2(aiAd+biASi)V Д § Vi2)2X 1 i /
х
Р(а,А
П1 1
d +bi ,
где
n
2(aiACi+biASi) Ј AS,2, i
Теперь для выражения (9) получим
AUi -Ui2 i ASi Si + n ,e 1
2
H-V5 UiUBr f-1 Ј -2, (10)
ni i /
где Uer - действующее значение напряжния высших гармоник UBr - Ј Ui2.
П| 1
Из зависимости (10) находим относителную погрешность
4U,-1«U 4
22 Ut2
KfHASif fljAS.Si) ni i
(1 Поскольку значения Si на интервалах (О, -п
7133
(W, я), (я, я), (-« я, 2я) повторяются, т выражение (11) запишется
П2
(EASi2)
+ §AS,S,),
n N 1
+
где m So 0000...0;
Sn2 1111...1; ASo 0; А8щ 0;
К - коэффициент пропорциональности.
Из выражения (12) видно, что относительная погрешность д Ui содержит две составляющие, причем вторая составляющая определяется суммой произведений величин A Si и Si. Следовательно, для уменьшения этой составляющей необходимо стремиться к тому, чтобы знаки менялись,
п2
тогда величину Т ASi Si можно уменьшить.
i 1
Расчет погрешностей коэффициентов Фурье (ai и bi) и действующего значения первой гармоники выполнялся на ЭВМ при двух видах округления численных значений 5 синуса в n точках периода: при симметричном округлении с разбросом до р двоичных разрядов. При симметричном округлении величины Si до ближайшего числа на р-разрядной сетке округленное значение 10 определяется из выражений:
5i Sip 0, у, , } ,2ysp, если у (pt,) О
Sip 0, yi. yi2. - .yip + , если yj(p4 1. Следовательно, можно записать
15
,т(
S, Sip +q где q 2 р;
р - натуральное число; mi /1 при округлении с избытком 2010 при округлении с недостатком.
Тогда для нахождения правила округления, минимизующего величину д Ui. необходимо найти такой выбор коэффициентов гщ (I
1,2,3па), при котором величина д до25 стигает минимума.
Таким образом, нужно найти такой набор коэффициентов ггн (i 1,2,3,402), который обращает в минимум величину d Ui в выражении (12). Поскольку общее число раз30 личных комбинаций величины т, равно , то в большинстве случаев эту оптимизационную задачу не возможно решить путем прямого перебора. Для этого используется известный метод случайного поиска Монте35 Карло. При этом на одной итерации j значения коэффициентов mi, равные 0 или 1, выбирались случайно, после чего вычислялось значение д Ui (mr.ma. тз гпп2 ) п°
40 формуле (12).
В таблице приведены относительные погрешности величины д Ut при округлении значений синуса с разбросом до 20 и 16 двоичных разрядов при К 0,001 и п 256
дс (значения 5Ui определялись первой суммой выражения (12), значения д иГ - второй суммой, а (5 Ut - суммарная погрешность; первый этап приближения соответствует симметричному округлению).
CQ Из таблицы видно, что округление с разбросом позволяет в несколько десятков раз уменьшить общую погрешность в сравнении с симметричным округлением (первая строка в таблице) за счет второй
55 СУММЫ выражения (12). Кроме того, после седьмой итерации (при р 20) погрешность уменьшилась с 123,68 до 5,9 Численные значения синусов, которые устанавливаются после последней итерации (оптимальное округление) с разбросом,
запоминаются и используются в дальнейшем при вычислении коэффициентов Фурье с наивысшей точностью по соотношениям;
J Ui(t,)G ni 1
(13)
iui(t,)S:
n, -1
Ј u2(ti)G
n,
i 1
ЈU2(tl)Sj.
ni 1
t arag||Mпри
1 arctg Ч-- при a1 0 и b1 0: . arctg I -I + Я при al 0 и Ы 0; arctg I -I +-7Г при al 0 и Ы 0. CIS)
Аналогично вычисляется величина по значениям коэффициентов Фурье 32 и D2. Разность фаз между синусоидальными величинами ui(t) и U2(t) определяется через начальные фазы
p ijH-ijJi.
Между коэффициентами Фурье ai, bi и действующим значением первой гармоники существует известная связь
Ui2 (ai2 + bi2).
Расчеты показывают, что погрешность расчета разности фаз р и начальных фаз VL № определяется погрешностью коэффициента Фурье ai и bi и разрядностью цифрового устройства, обеспечивающего вычисление разности фаз по значениям коэффициентов Фурье. В свою очередь, погрешность вычисления коэффициентов Фурье определяется прежде всего тем, до какого числа р двоичных разрядов производится округление численных значений синусов в n точках периода. Расчеты показывают, что, округляя синусы с разбросом до р двоичных разрядов, получаем численные значения коэффициентов Фурье с р верными знаками, т.е. погрешность расчета коэффициентов Фурье меньше единицы младшего разряда р-разрядного двоичного числа. Заметим, что при симметричном округлении погрешность коэффициентов Фурье больше единицы младшего разряда р-разрядного двоичного числа. Так,
при округлении синусов до 12 двоичных разрядов коэффициенты Фурье содержат 12 верных двоичных разрядов. Таким обра зом, при заданной разрядности коэффициентов
Фурье порядка р вычислительное устройство, обеспечивающее вычисление фазы по значениям коэффициента Фурье, должно быть р-разрядным. Расчеты на ЭВМ показывают, что относительная погрешность коэффициентов Фурье и действующего значения первой гармоники при симметричном округлении до 12 двоичных разрядов и числе точек на период n 256, составляет величину б Ui 4,49 10 , а при округлении с разбросом - д Ui 0,13 -10 . Принимая во внимание, что:
tgO, Г 0,00174533; tg0.01° 0,000174533, можно сделать вывод, что для измерения
разности фаз с погрешностью порядка 0.1° необходимо иметь разрядность цифрового устройства порядка 24 двоичных разрядов. Аналогичные расчеты погрешностей проведены при округлении синусов в n точках
периода до шести двоичных разрядов (р 6), до восьми двоичных разрядов (р 8), до шестнадцати (р 16) и до двадцати двоичных разрядов (р 20).
Расчеты показывают, что предлсженный способ обеспечивает измерение разности фаз от 0 до 360° в диапазоне; от инфранизких до высоких частот за время измерения порядка двух периодов исследуемого сигнала с погрешностью порядка
,1°.
Важными преимуществами способа являются отсутствие погрешности от влияния искажения формы сигнала, отсутствие погрешности от наличия в сигнале постоянной составляющей и отсутствие погрешности от отклонений уровней входных сигналов.
Измерение разности фаз в устройстве, реализующем способ, производится следующим образом.
Исследуемые сигналы m(t) и U2(t) подаются на входы преобразователей 1 и 6 аналог - код и блок 2 управления. С выходов преобразователей 1 м 6 коды мгновенных
значений сигналов ui(t) и Uji(t) поступают на первые входы вычислителей 3 и 7 коэффициентов Фурье. Одновременно на их вторые входы поступают коды §| численных значений соответствующих ступенек квазисинусоидальной функции, записанной в блоке 5. В конце периода исследуемого сигнала вычисление коэффициентов Фурье в вычислителях 3 и 7 заканчивается, и коды коэффициентов Фурье передаются в вычислители 4 и 8 для вычисления начальных фаз сигналов г/я. По начальным фаза/л сигналов в вычислителе 9 определяется разность фаз (р между сигналами ui(t) и ua(t) и индицируется в блоке 10.
В исходном состоянии триггеры счетчиков 12 и 18 и триггер 14 находятся в нулевом состоянии (цепи установки не показаны). Работа блока 2 управления происходит в два этапа: подготовительный и измерительный. Длительность каждого этапа равна длительности исследуемого сигнала Тх. Исследуемый сигнал ui(t) поступает на вход формирователя 11 импульсов блока 2 управления. При переходе исследуемого сигнала через нулевое значение из отрицательной области в положительную формирователем 11 вырабатывается импульс, который поступает на вход счетчика 12. Код, записанный в счетчике, дешифрируется и на его первом выходе появляется высокий потенциал, который устанавливает триггер 14 в единичное состояние. Теперь импульсы с выхода генератора 15 через открытый элемент И 16 поступают на счетный вход умножителя 17 частоты. Начинается процесс деления периода исследуемого сигнала Тх на п равных частей (умножители частоты). Когда на вход формирователя 11 поступает второй импульс, счетчик 12 изменяет свое состояние и на втором выходе дешифратора 13 появляется высокий потенциал, который поступает на управляющий вход умножителя 17 частоты. Период исследуемого сигнала Тх разделен на п равных частей. Подготовительный этап работы блока завершен, с этого момента начинается процесс измерения: на выходе умножителя 17 частоты появляется п равномерно распределенных по периоду Тх импульсов, которые поступают с одной стороны на преобразователи 1 и 6 аналог - код, задавая моменты преобразования аналогового сигнала в цифровой код. а с другой стороны - на вход счетчика 18 адреса, выходной код которого поступает на адресный вход блока 5 памяти. ,
При поступлении на вход формирователя 11 третьего импульса (момент окончания второго периода исследуемого сигнала) счетчик 12 в очередной раз изменяет свое состояние, и высокий потенциал появляется на третьем выходе дешифратора 13, что приводит к установке триггера 14 в нулевое состояние, элемент И 16 закрывается, тем самым доступ импульсов генератора 15 эталонной частоты на вход умножителя 17 и, следовательно, выработка импульсов последним не осуществляются. Работа блока 2 управления завершена.
Общее время измерения разности фаз вместе с предварительным измерением периода сигнала, перехода вычисления коэффициентов Фурье и временем вычисления
начальных фаз и разности фаз составляет два с небольшим периода. При известном периоде сигналов время измерения можно сократить на один период.
Использование предложенного способа измерения сдвига фаз по сравнению с известными обеспечивает повышение точности измерения сдвига фаз в широком диапазоне низких и инфранизких частот при сохранении разрядности цифрового вычислительного устройства. Способ отличается своей универсальностью, поскольку может использоваться для измерения разности фаз между первыми гармониками дву периодических несинусоидальных сигналов
для измерения разности фаз между первыми гармониками двух сигналов, когда один из них чисто синусоидальный, а второй периодический несинусоидальный, а также может использоваться и для измерения разности фаз между двумя чисто синусоидальными сигналами.
Формула изобретения Способ определения разности фаз, заключающийся в том, что выполняют прэобразование Фурье первых гармоник каждого из периодических сигналов с помощью квазисинусоидальной ступенчатой функции, определяют по коэффициентам Фурье фазу первой гармоники каждого из периодических сигналов, отличающийся гем, что, с целью повышения точности величины ступенек квазисинусоидальной функции определяют по минимуму относительной погрешности (5lJi среднеквадратического
значения первой гармоники периодического сигнала в соответствии с соотношением
д Ui К
2 V2
rSASi
VrT 1
+ UASiSib
2)1
где К - коэффициент гармоник сигнала; п - число выборок на период: .
п2-5-1:
Si - точные значения величин ступенек квазисинусоидальной функции в точках дискретизации;
A Si Si - Si - погрешности ступенек;
Si - приближенные значения ступенек функции в тех же точках, а разность фаз определяют, вычитая фазы первых гармоник периодических сигналов.
Результаты расчета на ЭВМ относительной погрешности действующего значения первой гармоники сигнала




| название | год | авторы | номер документа |
|---|---|---|---|
| Способ определения коэффициента гармоник | 1988 |
|
SU1629873A1 |
| Измеритель коэффициента нелинейных искажений | 1976 |
|
SU567147A1 |
| Способ измерения сдвига фаз | 1988 |
|
SU1553921A1 |
| Устройство контроля аналого-цифровых преобразователей | 1988 |
|
SU1711327A1 |
| Калибратор периодических сигналов | 1990 |
|
SU1795392A1 |
| Устройство для измерения характеристик каналов ФАР | 1989 |
|
SU1698838A1 |
| СПОСОБ ПЕРЕДАЧИ И ПРИЕМА ЗАКОДИРОВАННОЙ РЕЧИ | 2007 |
|
RU2343563C1 |
| Способ преобразования угла поворота вала в код | 1988 |
|
SU1786662A1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛА | 1993 |
|
RU2065168C1 |
| Измеритель нелинейных искажений | 1988 |
|
SU1642409A1 |
Изобретение может быть использовано для измерения разности фаз синусоидальных сигналов и первых гармоник несинусоидальных сигналов. Цель - повышение точности измерения. Способ измерения разности фаз включает определение коэффициентов Фурье первых гармоник каждого из периодических сигналов с помощью квазисинусоидальной ступенчатой функции, определение по коэффициентам Фурье фазы первой гармоники каждого из периодических сигналов, определение разности фаз вычитанием фазы первой гармоники одного периодического сигнала из фазы первой гармоники другого периодического сигнала, при этом величины ступенек квазисинусоидальной функции определяют по минимуму относительной погрешности среднеквад- ратического значения гармоники периодического сигнала из соотношения, приведенного в описании изобретения. Цель достигается за счет оптимального выбора ступенек по указанному соотношению. 1 табл., 2 ил.

| Цифровые методы измерения сдвига фаз/Под ред | |||
| Корндорфа, Новосибирск: Наука, 1979, с.41-42, рис | |||
| Устройство для электрической сигнализации | 1918 |
|
SU16A1 |
| Авторское свидетельство СССР № 1422855, кл | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1991-11-15—Публикация
1988-06-03—Подача