, Изобретение относится к обучающим математическим игрушкам.
Цель изобретения - повышение зани- маемости и расширение дидактических возможностей.
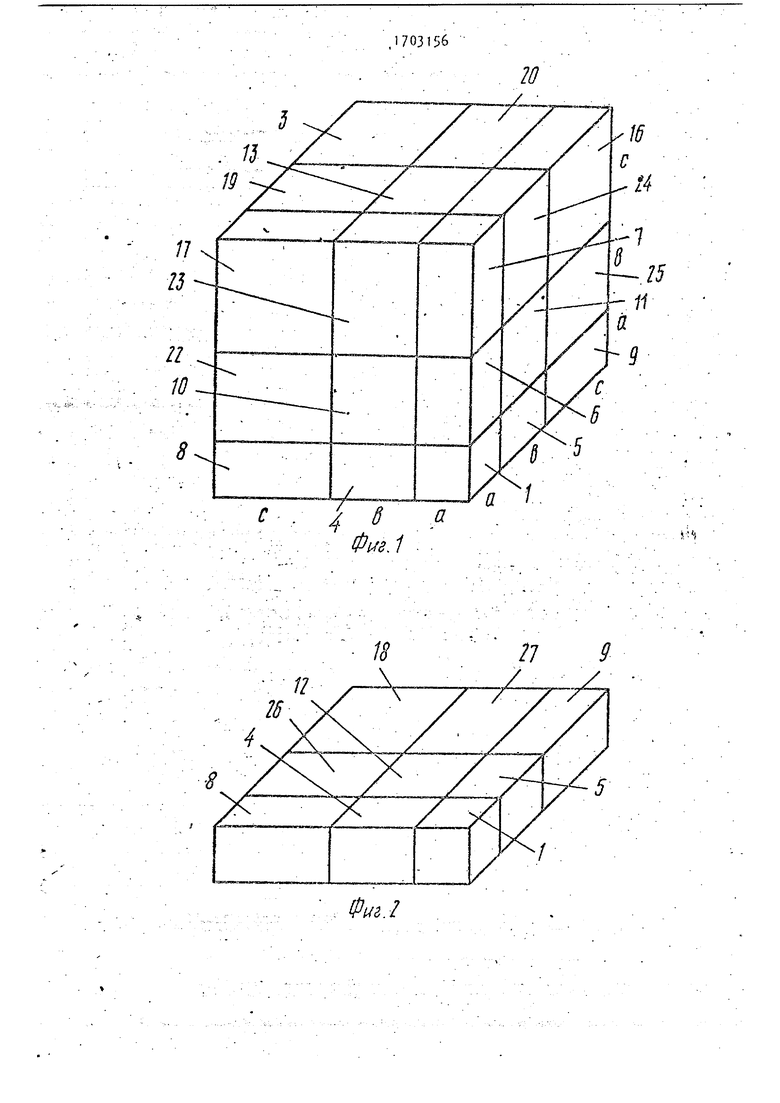
; На фиг. 1 изображена игрушка в сборе; на фи г, 2 - нижний ряд игровых элементов; на фиг, 3 средний ряд игровых элементов; на фиг. 4 - верхний ряд игровых элементов.
Учебная математическая игрушка выполнена по форме куба с соотношением между размерами ребер куба и составляющих егр параллелепипедов , где А - размер ребра куба, а а, Ь, с - размеры ребер параллелепипедов; и содержит двадцать семь
игровых элементов/ выполненных по форме параллелепипедов. Игровые элементы 1, 2, 3 имеют форму куба с ребрами соответственно a,a,a; b,b,b; с,с,с и соответственно с объемами as, bs, с3. Из остальных игровых элементов игровые элементы 4, 5, 6 имеют ребра а, а, Ь и объём аг.Ь, игровые элементы 7, 8, 9 имеют ребра а, а, с и объем а2«с, игровые элементы 10, IV, 12 имеют ребра Ь, Ь, а и объем Ь2.а, игровые элементы J3, 1, 15 имеют ребра Ь, Ь, с, объем Ь2 С, игровые элементы 16, 17, 18 имеют ребра с, с, а и объем , игровые элементы 19, 20t 21 имеют ребра с, с, Ь и объем c2ib, игровые элементы 22-27 имеют ребра а, Ь, с и объем а-Ь-с.
ж
,№
Р
а
3
Игровые элементы можно изготовить из плест/ ассы, дереве.
Из всех отдельных параллелепипедов математического представляющих собой модульные строите.;;и---е элементы, в силу их разных размеров, можно составлять большое колймество разнообразных объемных фигур, композиций,
моделей, которые каждому ребенку подскажут его фантазия или находящийся
рядом, старший...... . ./.,. v :: , .
Дети познакомятся с такими поня- тиями, как ширина, высота, длина. Можно дополнить игру чертежами., по которым ребенок будет составлять фигуру, и наоборот, предложить ребенку по построенной фигуре составить чертеж, т.е. ребенок в игре подойдет к основан черчения, пространственного мышления.
Основной вид игрушки математицеский куб - это общий куб с ребрами, равными a+b+с, в котором все пзрзллелепипеды сложены вплотную один к
другому.-.
Объем сложенного основного куба равен (a+b+с)3, он состоит из объема отдельных элементов-параллелепипедов, (а+Ь+с) +Ь3 +с3+3аг b-t-ЗЬ2 а+ЗЬ2 с+ +3с2 -а-5-Зс2 Ь+ба-b- с, т.е. основной куб представляет материальную интерпретацию математического выражения третьей степени, о именно формулу возведения в третью степень суммы трех слагаемых, . .
С помощью составляющих куба, имеющих грани с ребрами двух разных размеров, например, с ребрами размеров а и Ь, можно составить куб размером меньше основного, с ребрами а+Ъ,
(а+Ь)3 а3+Ь3+За2 -Ь+За-Ь2,
, 031564
-/
т.е. взяв кубики: два куба объемом а3 и -Ь3 и шесть брусков объемом а - Ь и а-Ь2 можно наглядно представить , формулу возведения в третью степень суммы двух слагаемых т.е. малыши наглядно на объемных предметах уже в раннем возрасте познакомятся с математическими понятиями средней школы.
10 Если же включить в игру параллелепипеды (кирпичики) с тремя разными размерами ребер (а, Ь, с), то поставленные в разные положения, они наглядно представляют все элементы из15 вестных в математике соединений - . перестановок из трех элементов, размещение, сочетание, т.е. дети познакомятся в игре и с этими математическими понятиями. .
. . .
Формула изобретения
Учебная математическая игрушка по форме куба, содержащая двадцать семь игровых элементов, выполненных по форме параллелепипедов, о т л и ч а-- ю щ а я с ,я тем, что, с целью, повышения занимательности и расширения дидактических возможностей, три из
игровых элементов имеют форму куба с ребрами соответственно а, а, а; Ь5 Ь, Ь; с с, с и объемами соответственно а3, Ь3,.с3, а из остальных игровых элементов три имеют ребра
as a, b и объем , три имеют ребра а, а, с и объем а2,с, три имеют ребра Ь, Ь, а и объем Ь2.я, три имеют ребра Ь,.Ь, с и объем Ь2-с, три имеют ребра с, с, а и объем с2.а,
три имеют ребра с, с, Ь и объем с2-Ь, шесть имеиэт ребра а, Ь, си объем а-b -с.
8
с . 4
W 14
Фиг. 1 

| название | год | авторы | номер документа |
|---|---|---|---|
| ОБЪЕМНОЕ ИГРОВОЕ УСТРОЙСТВО В ФОРМЕ КУБА "МАГИЧЕСКИЙ КУБ" | 1998 |
|
RU2132712C1 |
| ИГРОВОЙ КУБИК | 1991 |
|
RU2011398C1 |
| ЛОГИЧЕСКАЯ ИГРА "ИНФОРМАЦИОННЫЕ КУБИКИ АРЕСТА" | 1993 |
|
RU2070080C1 |
| ОБЪЁМНОЕ ИГРОВОЕ УСТРОЙСТВО В ФОРМЕ КУБА "ЛАТИНСКИЙ КУБ" | 2017 |
|
RU2664247C1 |
| НАБОР ИГРОВЫХ ЭЛЕМЕНТОВ ДЛЯ МАТЕМАТИЧЕСКИХ ИГР | 1995 |
|
RU2129035C1 |
| ОБЪЕМНАЯ ИГРА-ГОЛОВОЛОМКА | 2009 |
|
RU2403946C1 |
| СПОСОБ ФОРМИРОВАНИЯ ОБЪЕМНОГО ТЕЛА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1990 |
|
RU2016614C1 |
| Способ оценки психической активности детей с тяжелой черепно-мозговой травмой | 2017 |
|
RU2681712C1 |
| ГОЛОВОЛОМКА ЮРИМОВА "ЧАК-ЧАК" | 1997 |
|
RU2125476C1 |
| Кулисно-рычажный механизм преобразования кривых | 1987 |
|
SU1482824A1 |

Изобретение относится к обучающим математическим игрушкам и позволяет повысить занимаемость -; расширить дидактические возможности. Учебная математическая игрушка выполнена по форме куба и содержит двадцать семь игровых элементов, выполненных по форме параллелепипедов, jTpn из игровых элементов имеют форму куба с с; ребрами соответственно а, а, а; Ъ, Ь, Ь; с с, с, и соответственно с объемами а3 , Ъ3, с3. Из остальных игровых элементов три имеют ребра а, а, Ь и соответственно объем а2 Ь; три имеют ребра а, а, с и объем три имеют объем Ь, Ь, а и объем b2.a три имеют ребра Ь, Ь, с и объем Ь2 три имеют ребра с, с, а и объем с2.а; три имеют ребра с, с, Ь и объем с2-Ъ, шесть имеют ребра а, Ь, с и объем а«Ь С. Из игровых элементов можно составлять большое количество разнообразных объемных фигур. Игрушка-куб представляет материальную интерпри- тацию математического выражения третьей степени, а именно формулу возведения в третью степень суммы трех слагаемых, h ил.
Фм.2
10
и
и
15
Фиг.4
U.
| Никитин Развивающие игры, М., 1985, с | |||
| Способ запрессовки не выдержавших гидравлической пробы отливок | 1923 |
|
SU51A1 |
Авторы
Даты
1992-01-07—Публикация
1989-10-23—Подача