Vui.1
Изобретение относится к средствам механизации графических работ, в частности к механизмам для преобразования кривых линий.
Преобразователь может быть использован для синтеза механизмов, предназначенных для воспроизведения алгебраических кривых в высших и средних специальных учебных заведениях. Кине- матическая схема механизма может быть использована также при конструировании устройств, рабочие органы которых должны вести некоторую точку по заданной траектории.
Цель изобретения - повышение удобства в работе за счет упрощения процесса преобразования кривых.
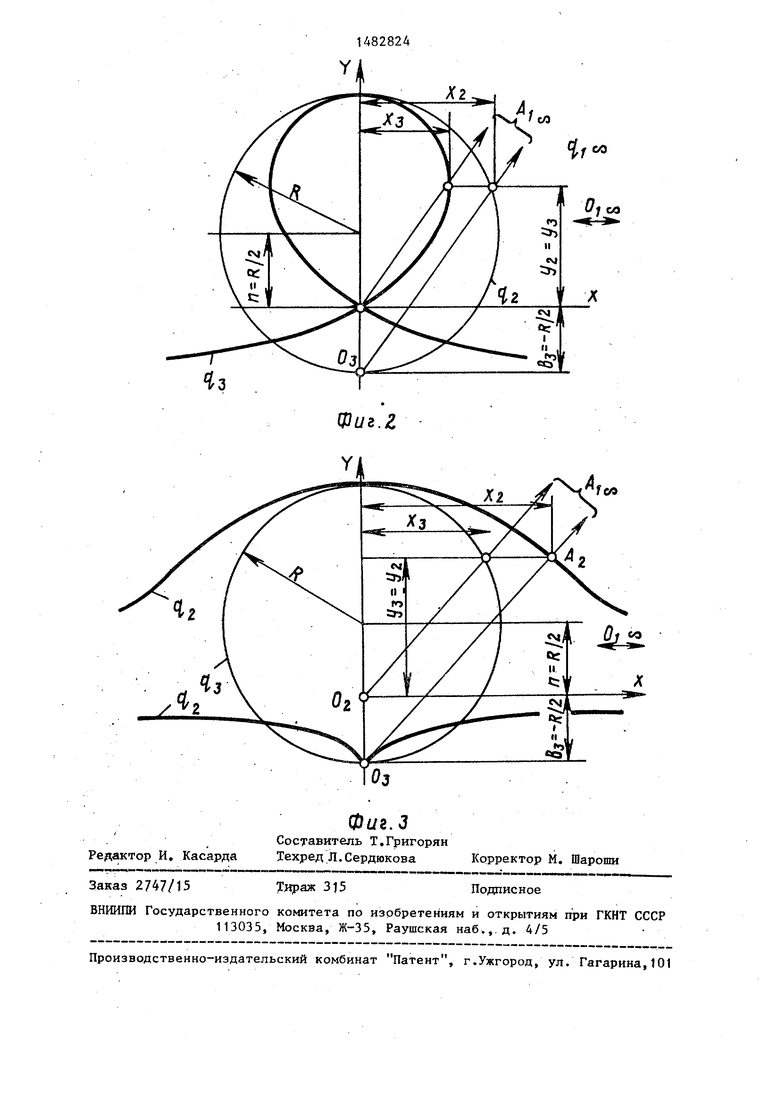
На фиг. 1 изображен механизм, общий вид; на фиг. 2 - воспроизведение механизмом кривой 3-го порядка (трисектрисы Маклорена); на фиг. 3 - воспроизведение механизмом кривых (цис- соиды Диоклесса, строфоиды).
Кулисно-рычажный механизм содер- жит установленные в прорези основания 1 переставные и фиксируемые шарниры 2 и 3 (точки 02, 03), связанные с ними одним концом кулисы 4 и 5, траверсу 6, соединенную с кулисами 4 и 5 посредством крестообразных ползунов 7 и 8, 9 и 10 соответственно в точках А2 и А3, и вертикальную направляющую 11 с ползуном 12, связанным с концом траверсы 6. ,
Кулисно-рычажный механизм имеет шарнирно соединенный со свободными концами кулис 4 и 5 в точках С и D и расположенный над крестообразными ползунами 7 и 8, 9 и 10 рычаг 13. При этом кулисы 4 и 5 расположены параллельно одна другой, образуя с рычагом 13 и прорезью основания 1 шарнирный параллелограмм.
Кулисы 2 и 3 подвижно связаны с траверсой 4 диадами из ползунов 6 и 7, 8 и 9 соответственно в точках А2 и А3. В точках С и D кулисы 2 и 3 шарнирно соединены звеном 10 так, что образуют с основанием 1 шарнирный параллелограмм 02 СП03, у которого 0203 CD, 02C -03D. Переставные шарниры 2 и 3 в точках 02 и 03 прорези основания 1 жестко фиксируются с помощью гаек-барашек .14.
I
В основу работы кулисно-рычажного
механизма положено обобщенное преобразование Маклорена, позволяющее строить алгебраические кривые разного типа и порядка по единому алгоритму. На фиг. 2 показано прямое преобразование окружности q2 в кривую Т3 из семейства кривых Крамера. Здесь центр преобразования 03 расположен на конце вертикального диаметра преобразуемой окружности q2 радиуса R; центр 02 - на этом же диаметре, но не принадлежит окружности, а центр О
1оо
- несобственная точка оси 02 X
прямоугольной декартовой системы координат Х02У. Осью преобразования служит несобственная линия .
Построение точек, принадлежащих преобразованной кривой q3, осуществляют в следующей последовательности
Из центра 03 проводят под произвольным -углом проецирующий луч и отмечают точки А1оо и А2 его пересечения с осью преобразования преобразуемой кривой q2. Из центра 02 через точку 01оо проводят луч.(он будет параллельным лучу 03А2). Из центра преобразования через точку А2 проводят проецирующий луч (он будет параллельным оси 02Х). В пересечении лучей О
оо 2
и 02А1оо
жит преобразованной кривой q3. Повторяя построения, получают требуемое количество точек кривой q3.
На фиг. 3 показано обратное преобразование окружности. В этом случае подучена кривая их семейства конхонд.
Кулисно-рычажной механизм работает следующим образом.
Если точку А2 (фиг. 1) вести по некоторой линии q,, определяемой уравнением F(X2Y25 0, то кулисы 4 и 5 вращаются вокруг осей шарниров 02 и 03, а ползун 12 траверсы 6 перемещается по вертикальной направляющей 11. При этом ползуны 9 и 10 перемещаются соответственно по кулисе 4 и траверсе 6S а точка А3 описывает кривую qa, определяемую уравнением Р (Х3, Ys) 0, Таким образом, указанная кинематическая цепь преобразует линию F(X2, Y2) 0 в кривую Р (Х3, Y3) 0 при несобственной оси преобразования q1co.
Если точку А3 вести по некоторой
линии F(X3, Y3) 0, то точка А2 описывает кривую Р(Х2, Y2) 0. Следовательно, кулисно-рычажной механизм устанавливает соответствие между плоскими полями точек А2 и Аэ ()
514828246
Выполнив проецирования и сечения Уравнения (5) и (6) описывают се- в аналитической форме, получают урав- мейства кривых 4-го порядка, несим- нения, устанавливающие зависимость метричньк относительно осей декарто- координат преобразованной точки А3 Вой системы координат Здесь индексы от координат преобразуемой точки А2 При X и Y опущены.
(прямое преобразование),..,, ,,л п
Пусть в уравнениях (5) и (6) а, О,
(X3-a2)(Y3-b.,)+a, lY3-b.)|R Р
. (1)Ь2 0, аэ 0, т- 0, n f и Ъ3 .
и3-ь2 10
Тогда из уравнения (5) имеют
2 х - v (7)
В обратном преобразовании имеютл V 2Y + R
(Х2 - аэ) (Y2 - Ь2) + а2 (Y2 Ь3 ) (3)i5 Это трисектриса Маклорена, которая изображена на фиг. 2. Аналогично
из уравнения 6 получают
(4)X (2Y + R) ) . (8)
20
Из аналитических взаимоотношении
(3) и (4) между координатами соответ-Эта кривая, изображенная на
ственных точек двух плоских полей П2фиг. J.
и П3 следует, что для получения вза- Если в уравнении (6) принять
имоотношений в обратном преобразова-го - J, п - R, а2 - О, Ь2 0, а3 О,
нии достаточно в уравнениях (1) и (2) 5 Ьз 2R то получают циссоиду Диокпри алгебраических членах поменятьлесса
индексы 2 на 3 и 3 на 2. Таким обра-Y3
V2 ц,(Q}
зом, указанное соответствие между2R - Y
точками полей IL и II. взаимно однозначное.30 в « лУчае когда в уравнении (6)
В выражениях (1)-(4) а2, Ь2, а, п 0, m 0, а2 О, Ь2 0, а, О, и Ь3 - параметры кулисно-рычажного Ьз R то имеют строфоиду механизма. Изменение их осуществляется перестановкой шарниров 02 и 03 в i
прорези основания 1, а также измене- 35 2 Y2 . (10) нием длины рычага 13 (фиг. 1),R + Y
Для уравнения, получаемого при
преобразовании семейства крив1 :, не- .
аФормулаизобретения
обходимо значения координат уравнений (1) и (2) или (3) и (4) под- 40
v „Кулисно-рычажныи механизм преобставить вместо X и Y в уравнение„
л „ „- разования кривых, содержащий установпреобразуемои линии. Например, чтобы
ленные в прорези основания перестав- получить уравнение кривой, получаемой .
fv ч , ные и фиксируемые шарниры, связанные
при преобразовании окружности (Х-пи2 + J
+ (Y - п)2 - R, достаточно под -«5 С НИМИ °ДНИМИ КОНЦЯМИ КУЛИСЫ ТраВ6Р ставить значения Х2 и Y2 из уравне- Су соеДИНенную с кулисами посредст- ний (1) и (2) (прямое преобразование) ВОМ крестообразньк ползунов, и верили Х3 и У3 из уравнений (3) и (4) тикальную направляющую с ползуном, (обратное преобразование) вместо X связанным с концом траверсы, о т л ии Y уравнения окружности. Тогда соот-БО ющиися тем, что, с целью ветственно имеютповышения удобства в работе за счет
Г(Х -a)CY-b)+ (Y - Ъ 1 - упрощения процесса преобразования
-m(Y -% )12 +3 (Y -, )2 кривых, он имеет шарнирно соединен2- 2нъй со свободными концами кулис и (Y - п)2 - R2 0 (5)55 расположенный над крестообразными( Г(Х - а )(Y - b ) + а (У - Ь ) - ползунами рычаг, при этом кулисы
-m(Y -Ч Л2 +2(Y - Ь )2 Г(У - п)2 расположены параллельно одна другой,
3з Lобразуя с рычагом и прорезью основа-R2 0(6) ния шарнирньй параллелограмм.
У
, со

| название | год | авторы | номер документа |
|---|---|---|---|
| Механизм для воспроизведения лемнискаты Жероно | 1981 |
|
SU992234A1 |
| Кулисно-рычажный механизм преобразователя кривых | 1981 |
|
SU992233A1 |
| Прибор для воспроизведения эллипса и гиперболы | 1980 |
|
SU901069A1 |
| Прибор для вычерчивания кривых второго порядка | 1980 |
|
SU925682A1 |
| Шарнирно-рычажный механизм для воспроизведения кривых | 1983 |
|
SU1113284A1 |
| Кулисно-рычажный механизм Мамырина для воспроизведения трисектрисы Маклорена | 1984 |
|
SU1240632A1 |
| Шарнирно-рычажный механизм преобразователя кривых на основе дву-двузначного соответствия | 1986 |
|
SU1335488A1 |
| Прибор для вычерчивания трисектрисы Маклорена | 1987 |
|
SU1459950A1 |
| Механизм для преобразования окружности в кривые 3-го и 4-го порядка | 1980 |
|
SU901067A1 |
| Прибор для воспроизведения кривых | 1989 |
|
SU1655816A1 |
Изобретение относится к средствам механизации графических работ, в частности к механизмам для преобразования кривых линий. Оно позволяет повысить удобство в работе за счет упрощения процесса преобразования кривых. Противоположные концы кулис 4 и 5 шарнирно связаны между собой в точках C и D рычагом 13 так, что образуют с основанием 1 шарнирный параллелограмм O2CDO3, позволяющий воспроизводить кривые 2, 3, 4-го порядка. 3 ил.

| Шарнирно-рычажный механизм преобразователя кривых на основе дву-двузначного соответствия | 1983 |
|
SU1121161A1 |
| Зубчатое колесо со сменным зубчатым ободом | 1922 |
|
SU43A1 |
Авторы
Даты
1989-05-30—Публикация
1987-07-20—Подача