Изобретение относится к картографии, в частности к способам изготовления объемных моделей небесных тел - глобусов, которые могут быть использованы при решении прикладных задач космонавтики, для чтения лекций в планетариях, в учебных процессах в школах и вузах.
Известны способы изготовления шаровых глобусов, в основе которых лежит объемная шаровая модель, на которую наносятся сегменты карт одинаковой формы и размеров в видоизменной поликонической проекции, где плановые координаты одинаковы для всех сегментов. Примером могут служить глобусы Земли, глобусы звездного неба и т.д..
Наиболее близким к изобретению является способ изготовления глобуса Луны масштаба 1:10000000.
Однако для шаровых глобусов характерно недостаточное соответствие модели глобуса фигуре небесного тела при аппроксимации ее шаром, так как целый ряд небес- ных тел имеет геометрически более
сложные формы (фигуры) со значительным экваториальным и полярным сжатием.
Использование сегментов карт одинаковой формы и размеров в видоизмененной поликонической проекции непригодно для объемных моделей более сложной формы Получаемое по этим моделям восприятие физической поверхности небесных тел является искаженным.
Цель изобретения - максимальное обеспечение соответствия моделей небесных тел их физическим особенностям и, как следствие, повышение адекватности восприятия отображенной на глобусе реальной поверхности небесного тела, а следовательно, повышение точности решения прикладных задач космонавтики.
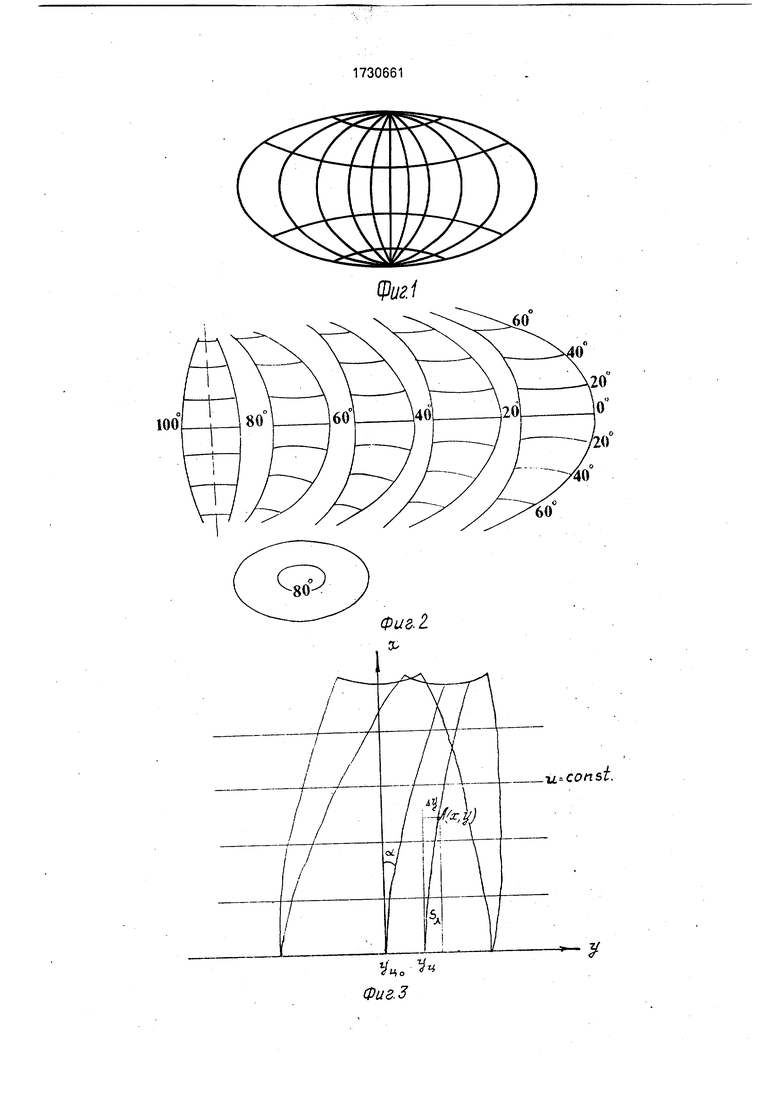
Цель достигается тем, что модель небесного тела выполняется в виде трехосного эллипсоида (фиг.1), а набор сегментов карт представляют в виде четырех одинаковых комплектов (фиг.2), при этом геометри- ческие параметры и конфигурацию
Ё
VI Сл)
О
о
ON
каждого сегмента определяют по следующим зависимостям (фиг.З):
X V о 22 ,
Н. у
Y (УЦ - Уцо) cos U + Ay, где где X, Y - прямоугольные координаты точек картографической сетки проекции для каждого сегмента;
$х - длины дуг меридианов, изменяю- щихся по долготам и широтам от экватора до параллели U const;
U - заданные параллели;
УЦ, Уцо - длины дуг отрезков экватора данного трехосного эллипсоида между за- данными и средними меридианами зон, получаемые при сохранении длин экватора;
Ду - поправки в ординаты и абсциссы за счет изменения кривизны эллипсов эква
тора и параллели.
На фиг.1 представлена модель небесного тела в форме трехосного эллипсоида, общий вид; на фиг.2 - комплект сегментов различной формы, обеспечивающих покрытие картами 1/4 части модели небесного тела (всего 4 симметричных части); на фи.З - геометрическая интерпретация системы координат точек эллипсоида.
Сущность способа заключается в использовании в качестве объемной модели небесного тела трехосного эллипсоида и разработке двух новых специальных картографических проекций трехосного эллипсоида для последующего построения картографического изображения сегментов с минимальными искажениями вдоль меридианов и параллелей. В первой предназна- ченной для картографирования всей поверхности без полюсов, сохраняются длины на экваторе и учитывается неортого- нальность проекций меридианов на плоскость экватора экваториальному эллипсу. Поскольку в каждом сегменте ординаты получают различные смещения, меридианы изображаются линиями, кривизна которых изменяется от сегмента к сегменту. Во второй, предназначенной для изображения полюсов, проекции сохраняются длины разных по величине меридианов трехосного эллипсоида.
Таким образом, заявляется глобус в форме трехосного эллипсоида, при создании которого соединяются в единую модель не просто отдельные элементы одинаковой формы и размеров, а разные по форме, кри- визне линий, размерам детали (сегменты), полученные с учетом параметров реального небесного тела и в совокупности образующие единую объемную модель в форме трех
осного эллипсоида, несущую на себе строго определенную и пространственно локализованную информацию о реальной поверхности небесного тела.
Примером конкретной реализации предложенного способа является создание глобуса поверхности естественного спутника Марса - Фобоса, фигура которого аппроксимируется трехосным эллипсоидом.
Использование трехосного эллипсоида в качестве объемной модели обеспечивает по сравнению с прототипом (шаровой моделью) уменьшение искажений и, следовательно, повышение точности при отображении поверхности небесного тела на глобусе, а также обеспечение максимального соответствия формы модели форме реального тела и, следовательно, формирование более адекватного, наиболее приближенного к реальности представления о небесном теле, его форме и структуре поверхности.
Формула изобретения
Способ изготовления модели небесного тела, заключающийся в том, что выполняют макет тела и обклеивают его картой, состоящей из набора отдельных сегментов, каждый из которых представляет собой скорректированную на объемный участок часть плоской карты, отличающийся тем, что, с целью повышения точности моделирования небесных тел, имеющих сжатие более 0,2, макет небесного тела выполняют в виде трехосного эллипсоида, а набор сегментов выполняют из четырех одинаковых комплектов, при этом конфигурацию каждого сегмента определяют по следующим зависимостям:
X V с 2 W2 , SA y
Y (УЦ - Уцо) cos U + Ay,
где X, Y - прямоугольные координаты точек картографической сетки проекции для каждого сегмента;
Зд - длины дуг меридианов, изменяющихся по долготам и широтам от экватора до параллели;
U - заданные параллели; Уц, Уцо - длины дуг отрезков экватора данного трехосного эллипсоида между заданными и средними меридианами зон, получаемые при сохранении длин экватора:
Ау- поправки в ординаты и абсциссы за счет изменения кривизны эллипсов экватора и параллели.

Изобретение используют для изготовления объектов картографии - моделей небесных тел, имеющих сжатие более 0,2. Способ заключается в том, что модель небесного тела выполняют в виде трехосного эллипсоида, поверхность которого обклеивают картой, состоящей из набора отдельных сегментов, включающего четыре одинаковых комплекта, при этом конфигурацию каждого сегмента определяют по определенным математическим зависимостям. 3 ил.
й/2/
О
Уч. «
| СПОСОБ ПОЛУЧЕНИЯ ТОПЛИВНЫХ БРИКЕТОВ | 2002 |
|
RU2227803C1 |
Авторы
Даты
1992-04-30—Публикация
1989-11-10—Подача