Изобретение относится к области вычислительной техники и может быть использовано в специализированных вычислительных машинах и устройствах обработки сигналов для перемножения двух (nxn) матриц.
Цель изобретения сокращение аппаратурных затрат.
На фиг.1 представлена структурная схема устройства для перемножения двух (nxn) матриц; на фиг.2 структурная схема устройства для n 3; на фиг.3 схема вычислительного модуля первого типа; на фиг.4 схема вычислительного модуля второго типа.
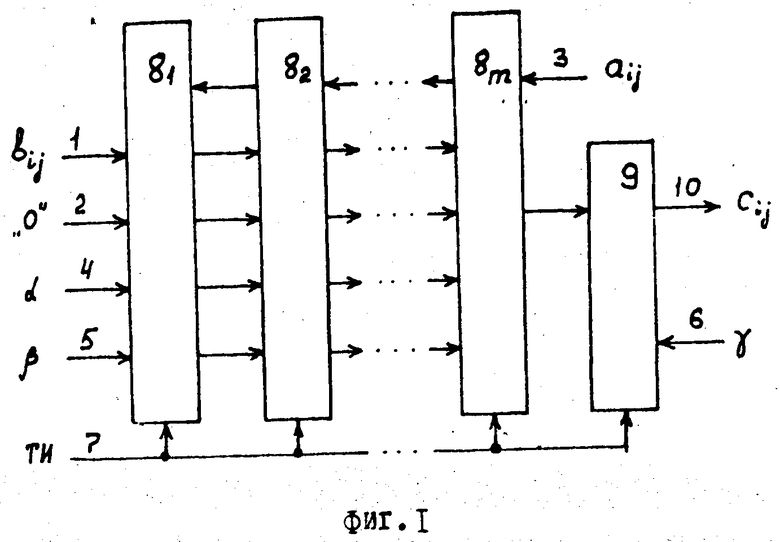
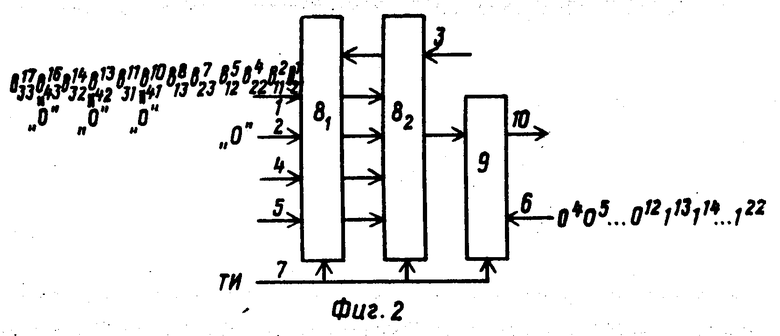
Устройство для перемножения двух (nxn) матриц (фиг.1) содержит первый 1, второй 2 и третий 3 информационные входы, первый 4, второй 5 и третий 6 настроечные входы, синхровходов 7, вычислительные модули первого типа 8i (i 1, m), вычислительный модуль второго типа 9 и выход 10.
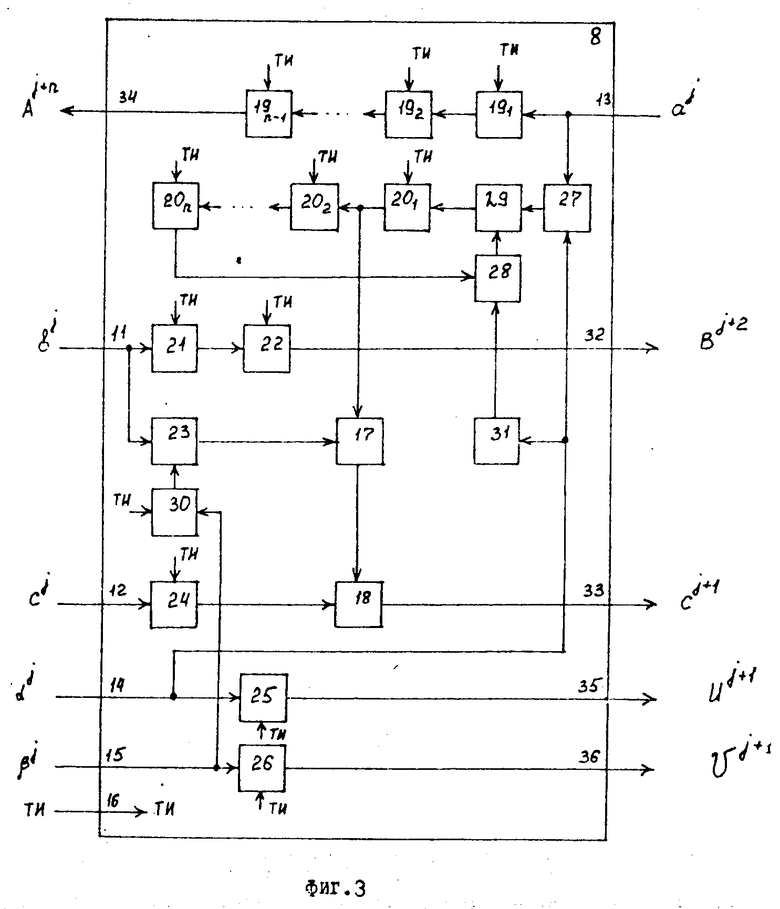
Вычислительный модуль 8 первого типа (фиг.3), содержит первый 11, второй 12 и третий 13 информационные входы, первый 14 и второй 15 настроечные входы, синхровход 16, умножитель 17, сумматор 18, регистры 19i (i 1, n-1), 20i (i 1,n), 21, 22, 23 и 24, триггеры 25 и 26, группы элементов И 27 и 28, группу элементов ИЛИ 29, элемент И 30, элемент НЕ 31, первый 32, второй 33 и третий 34 информационные выходы, первый 35 и второй 36 настроечные выходы.
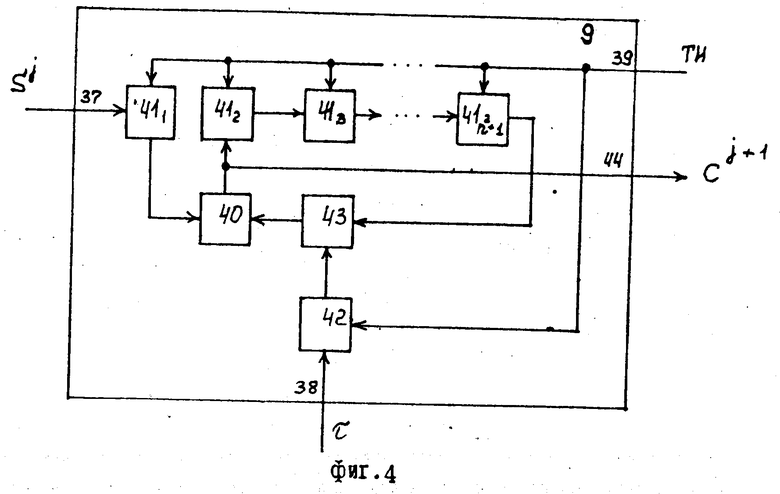
Вычислительный модуль 9 второго типа (фиг.4) содержит информационный вход 37, настроечный вход 38, синхровход 39, сумматор 40, регистры 41i (i 1, n2+1), триггер 42, группу элементов И 43 и выход 44.
В основу работы устройства положен следующий алгоритм. Пусть требуется перемножить две матрицы Aaik} и Bbkj} результатом перемножения которых является матрица С А, Вcij} i, j, k 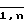 . Обозначим P
. Обозначим P 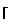 n/m
n/m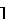 , где
, где 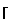 n/m
n/m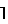 ближайшее целое сверху, m некоторое выбранное число, K
ближайшее целое сверху, m некоторое выбранное число, K 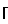 n/m
n/m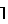 .
.
Будем считать, что в матрицах А и В соответственно К столбцов и К строк (1 ≅ k ≅ K). Если K≠ n, то следует добавить соответствующее число нулевых строк и столбцов, чтобы выполнилось равенство К n.
Элементы матрицы С вычисляются по следующим выражениям:
Cij=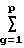 Sijq;
Sijq; 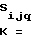 =
=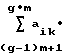 bkj,
bkj,
1≅ i,j ≅ n,≅ 1 q≅ P, которые определяются рекуррентными соотношениями:
1≅ i,j ≅ n 1 ≅ q ≅ P;
S((q-1)m)ijq 0;
(q-1)m+1 ≅ k ≅ q˙ m;
S(k)ijq S(k-1)ijq+aik ˙bkj.
Sijq S(q˙ m)ijq;
C(1)ij Sij1;
2 ≅ q ≅ P;
C(q)ij C(q-1)ij+Sijq.
Cij Cij(P).
Рассмотрим работу вычислительных модулей.
Вычислительный модуль 8 первого типа (фиг.3) работает в четырех режимах. Режим работы задается управляющими сигналами α и β подаваемыми соответственно на настроечные входы 14 и 15. Во всех четырех режимах вычислительный модуль 8 наполняет общие следующие операции. Элемент а, подаваемый на вход 13, задерживается регистрами 19 на n-1 тактов и выдается на выход 34. Элемент b, подаваемый на вход 11, задерживается регистрами 21 и 33 на два такта и выдается на выход 32. На выходе сумматора 18 формируется значение c' c+a b, где c' и a b значения, подаваемые на входы сумматора 18, соответственно с выходов регистра 24 и умножителя 17.
В первом режиме подаются управляющие сигналы α β (1.1). При этом группа элементов И 27 открыта, группа элементов И 28 закрыта, элемент И 30 открыт и в регистры 201 и 21 записываются соответственно элементы a и b.
Во втором режиме подаются управляющие сигналы ( α β) (1.0). Группа элементов И 27 открыта и в регистр 201 записывается элемент а. В регистре 23 хранится ранее записанный элемент b.
В третьем режиме подаются управляющие сигналы ( α β) (0.1). Элемент И 30 открыт и B регистр 23 записывается элемент b. В регистрах 20i(i=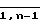 ) информация переписывается из 20i-го регистра в 20i+1-й регистр.
) информация переписывается из 20i-го регистра в 20i+1-й регистр.
В четвертом режиме подаются управляющие сигналы ( α β) (0.0). В этом режиме в регистре 23 хранится ранее записанный элемент 8 и в регистрах 20i(i= 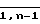 ) информация переписывается из 20i-го регистра в 20i+1-й регистр.
) информация переписывается из 20i-го регистра в 20i+1-й регистр.
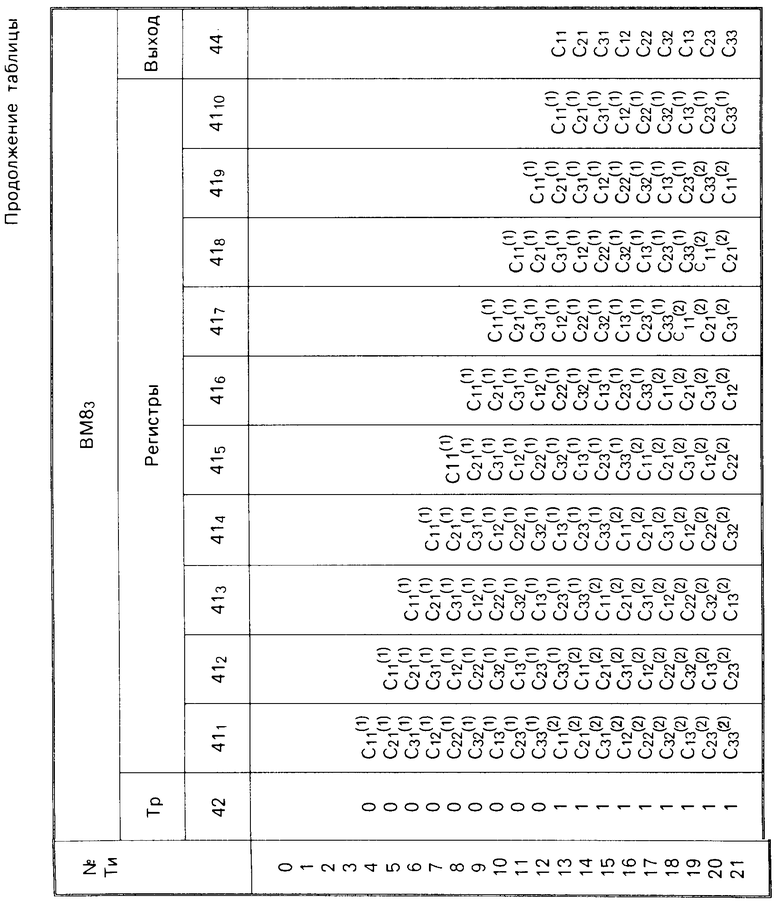
Вычислительный модуль 9 второго типа (фиг.4) работает следующим образом. На вход 37 последовательно подаются значения Ci (i 1,2.), которые записываются в регистр 411. При нахождении триггера 42 в нулевом состоянии, группа элементов И 43 закрыта, на первый вход сумматора 40 подается элемент Сi, а на второй вход нулевое значение, на выходе сумматора 40 формируется значение элемент Ci, которое записывается в регистр 412. Таким образом, при нахождении триггера 42 в нулевом состоянии происходит последовательная запись элементов Ci в соответствующие регистры 41. При установлении триггера 42 в единичное состояние, группа элементов И 43 открыта, через которую на первый вход сумматора 40 подается содержимое c регистра 41 n2+1-го, на второй вход сумматора 40 подается содержимое ci регистра 411 и на выходе которого формируется значение ci+c'i, которое записывается в регистр 412 и подается на выход 44.
Рассмотрим работу устройства для случая n 3 и m 2 (фиг.2). При этом P 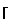 n/m
n/m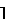 и K m, P 4.
и K m, P 4.
На вход 3 элементы ai, p+(q-1)m подаются в моменты времени
ta i-1+(P-1+(q-1)m)n+(n-m)(q-1)n, где P 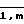 и q
и q 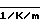 .
.
На вход 1 элементы bp+(q-1)mj подаются в моменты времени
tb (m-1)(n-1)+(q-1)n2-(m-1)+(j-1)n+(m-p).
Управляющие сигналы τ ij ( α, β) ij 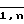 представляются в виде матрицы
представляются в виде матрицы

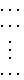
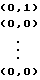
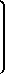 которые подаются на входы 4 и 5 в моменты времени
которые подаются на входы 4 и 5 в моменты времени
tτ (m-1)(n-1)+i-1+(j+1)n+(q-1)n2.
При перемножении двух матриц А и В на вход 2 постоянно подается нулевое значение. Если требуется перемножить матрицы А и В и сложить их с матрицей С, то на вход 2 подаются элементы матрицы Sijo(o)cij(o)в моменты времени
tC(o) (m-1)(n-1)+i-1+(j-1)n.
На вход 6 подается последовательность управляющих сигналов
0(m-1)(n-1)+m 0(m-1)(n-1)+m+n2-1 1(m-1)(n-1)+m+n2
1(m+n)(n-1)+(K/m-1)n2+m+1.
На выходе 10 формируются элементы Cij результирующей матрицы в моменты
tc (m-1)(n-1)+i+(j-1)n+(K/m-1)2n+m.
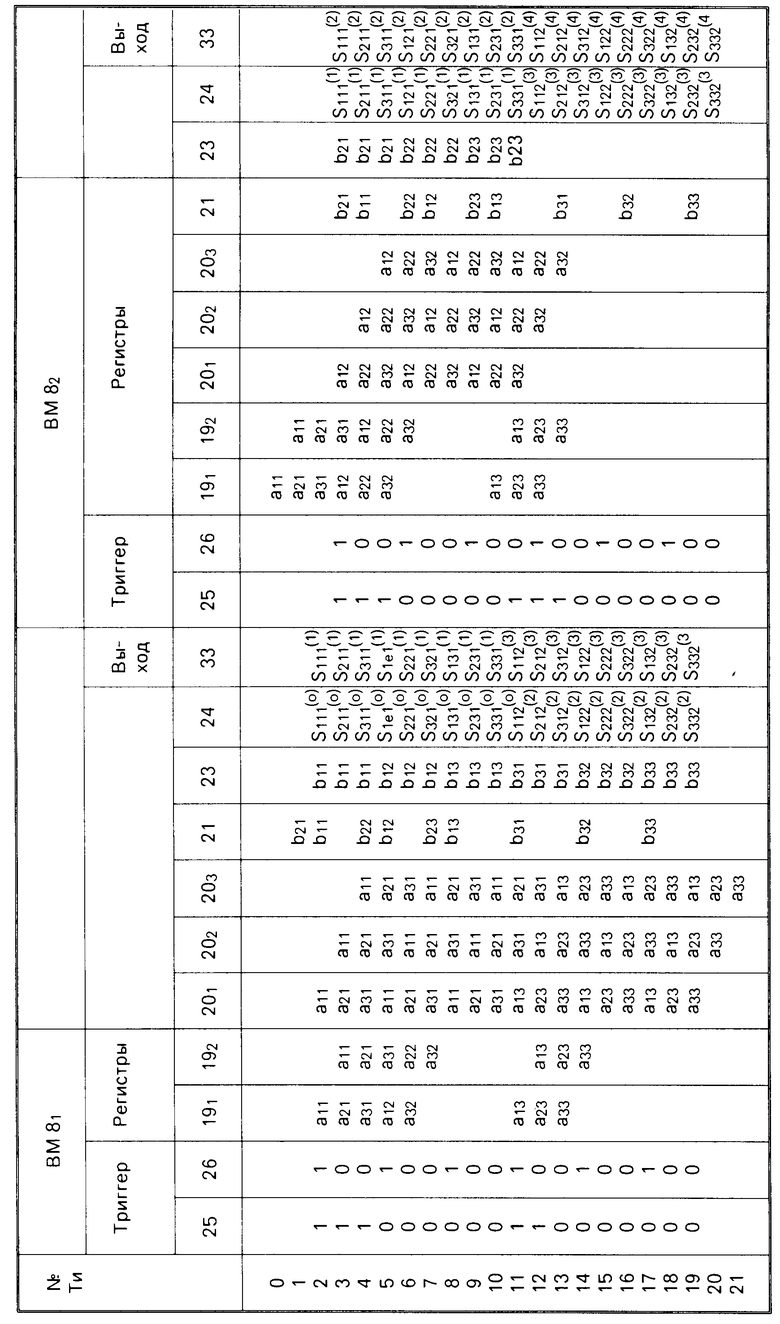
В соответствии с приведенными выражениями организация входного и выходного потоков данных для n 3 и m 2 приведена на фиг.2. В таблице приведены состояния триггеров, регистров и значения на выходах вычислительных модулей устройства. Рассмотрим работу устройства при формировании элемента С11 9. В вычислительном модуле 81 на втором такте формируется элемент S111(1) S111(0) + a11b11, на одиннадцатом такте элемент S112(3)S112(2) + a13 x b31. В вычислительном модуле 82 на третьем такте формируется элемент c(1)11 S(2)111 S(1)111 + a12b21, на двенадцатом такте элемент с(2)11 S(4)112 S(3)112. В вычислительном модуле 9 на тринадцатом такте формируется значение с11 с(1)11 + +с(2)11, которое выдается на выход 10 устройства. Аналогичным образом формируются остальные элементы cij. Последний элемент cnnформируется на ((m-1)n+P n2+1)-м такте.
| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для перемножения ленточных матриц | 1990 |
|
SU1774348A1 |
| Устройство для умножения матриц | 1990 |
|
SU1793446A1 |
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ТРЕХ МАТРИЦ | 1990 |
|
RU2024932C1 |
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ ТРЕХ МАТРИЦ | 1990 |
|
RU2024933C1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ СОБСТВЕННЫХ ЗНАЧЕНИЙ (N X N)-МАТРИЦЫ | 1992 |
|
RU2012050C1 |
| Устройство для перемножения потока @ - матриц | 1990 |
|
SU1797128A1 |
| Устройство для умножения матриц | 1989 |
|
SU1677709A1 |
| Устройство для вычисления собственных значений ( @ @ @ ) - матрицы | 1989 |
|
SU1721611A1 |
| УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ МАТРИЦ | 1991 |
|
RU2011221C1 |
| УСТРОЙСТВО ДЛЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ | 1991 |
|
RU2012049C1 |
Изобретение относится к области вычислительной техники и может быть использовано в специализированных вычислительных машинах и устройствах обработки сигналов для перемножения (n n)-матриц. Цель изобретения - сокращение аппаратурных затрат. Поставленная цель достигается тем, что устройство содержит m вычислительных моделей первого типа, и вычислительный модуль второго типа, причем каждый вычислительный модуль первого типа содержит умножитель, сумматор, две группы регистров, два триггера, две группы элементов И, группу элементов ИЛИ, элемент НЕ и элемент И, а вычислительный модуль второго типа содержит сумматор, группу регистров, группу элементов И и триггер. В основу работы устройства положена параллельно-поточная организация вычислений. Перемножение (n n) - матриц осуществляется с помощью фиксированного числа m вычислительных модулей (m < n). 4 ил., 1 табл.
УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ МАТРИЦ, содержащее m вычислительных модулей первого типа (m фиксированное число, m ≅ n, n размерность перемножаемых матриц), причем первый и второй информационные входы и первый настроечный вход устройства соединены соответственно с первым и вторым информационными входами и первым настроечным входом первого вычислительного модуля первого типа, первый и второй информационные входы и первый настроечный выход i-го вычислительного модуля первого типа (i 1, m 1) соединены соответственно с первым и вторым информационными входами и первым настроечным входом (i + 1)-го вычислительного модуля первого типа, синхровходы m вычислительных модулей первого типа соединены с синхровходом устройства, отличающееся тем, что, с целью сокращения аппаратурных затрат, в него введен вычислительный модуль второго типа, третий информационный вход которого соединен с третьим информационным входом m-го вычислительного модуля первого типа, третий информационный вход i-го вычислительного модуля первого типа соединен с третьим информационным выходом (i + 1)-го вычислительного модуля первого типа, второй настроечный вход устройства соединен с вторым настроечным входом первого вычислительного модуля первого типа, второй настроечный выход i-го вычислительного модуля первого типа соединен с вторым настроечным входом (i + 1)-го вычислительного модуля первого типа, третий настроечный вход устройства соединен с настроечным входом вычислительного модуля второго типа, информационный вход которого соединен с вторым информационным выходом m-го вычислительного модуля первого типа, а синхровход с синхровходом устройства, причем каждый вычислительный модуль первого типа реализует следующие функции: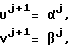
где αj, βj значения управляющих сигналов a и b соответственно на первом и втором настроечных входах вычислительного модуля на j-м такте,
Uj+1 и Vj+1 значения управляющих сигналов U и V соответственно на первом и втором настроечных выходах вычислительного модуля на (j + 1)-м тактах,
Aj+n-1= aj ,
Bj+2 bi,
Cj+1 cj + d · e,
где d = aj· αjVaj-n· βj,
где
e = bj· βjVbj-p·βj ,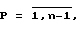
aj, bj и cj значения соответственно на третьем, первом и втором информационных входах вычислительного модуля на j-м такте,
Aj, Bj и Cj значения соответственно на третьем, первом и втором информационных входах вычислительного модуля на j-м такте,
а вычислительный модуль второго типа реализует следующие функции: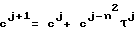
где cj значение на информационном входе вычислительного модуля на j-м такте,
t значение на настроечном входе вычислительного модуля на j-м такте.
| Релейный регулятор | 1989 |
|
SU1695263A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1995-05-27—Публикация
1990-07-30—Подача