Гармонический анализ сложных периодических кривых в том виде, в каком он предлагается в настоящее время, представляет много затруднений, вследствие отвлеченного характера и сложности этого анализа. Гораздо проще и понятнее его сущность становится в том случае, если подойти к вопросу, напр., с точки зрения колебательных движений, возбуждаемых в упругом теле силами, изменяющимися периодически по закону какой-либо сложной кривой.
Допустим, что имеем сложную периодическую кривую сил поршневого двигателя с периодом t. Такая сложная периодическая кривая может вызвать целый ряд гармонических вибраций в какой-либо из частей двигателя, во всем двигателе, в связанном с ним фундаменте и т.д. Упругие силы всех этих вибраций пропорциональны перемещению вибрирующих тел, т.-е. эти вибрации являются простыми гармоническими с постоянным периодом, так называемым «естественным» или «собственным» периодом вибраций.
Рассматривая данную периодическую кривую сил двигателя (фиг. 1), попытаемся определить, могут ли эти силы вызвать вибрации с периодом, равным периоду t.
Разделим этот период на две равные части и представим себе какую-либо часть двигателя, напр., коленчатый вал, вибрирующий с естественным периодом, равным t. Допустим, что в течение первой половины этого периода эта часть двигателя колеблется около своего среднего положения в одну сторону, в течение второй половины - в другую, как это показано кривою Р на фиг. 1. Очевидно, что от L до N силы нашей кривой направлены в сторону колебательного движения вала, т.-е. содействуют этому движению в то время, как от N до М эти силы направлены в сторону, противоположную колебательному движению, т.-е. противодействуют ему. Таким образом, в концекаждого периода колебательное движение тела поглощает импульс сил, равный разности площадей А и В.
Начерченная под данною кривою гармоническая кривая Р представляет собою то колебательное движение с периодом t, которое соответствует импульсу А-В. Этот импульс поглощается гармоническим импульсом молекулярных сил тела, колеблющегося также с периодом t. Обозначим этот период через 2π. Как не трудно убедиться,  , где Р1 равно максимальному напряжению колеблющегося тела и пропорционально амплитуде его колебаний.
, где Р1 равно максимальному напряжению колеблющегося тела и пропорционально амплитуде его колебаний.
Найденная синусоида 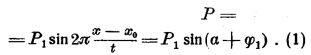
еще не определяет собою того гармонического колебания, которое возникает при действии сил указанной диаграммы. В самом деле, наряду с найденной синусоидой, может существовать и другая с углом сдвига, равным  , максимальное напряжение
, максимальное напряжение 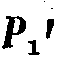 которой не могло найти себе выражения в формуле (1).
которой не могло найти себе выражения в формуле (1).
Для определения этого 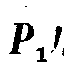 , переденнем ординаты Y1 и Y2 (фиг. 1) на четверть периода указанной периодической кривой, т.-е. в положение, показанное на фиг. 2. Разность А′-В′ даст нам выражение для определения
, переденнем ординаты Y1 и Y2 (фиг. 1) на четверть периода указанной периодической кривой, т.-е. в положение, показанное на фиг. 2. Разность А′-В′ даст нам выражение для определения 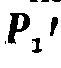 :
:
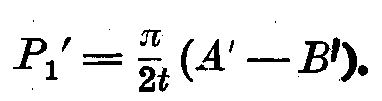
Таким образом, вторая синусоида с периодом, равным t, будет иметь следующий вид:

Общий вид нашей гармонической кривой с периодом t будет:
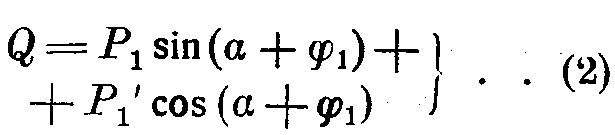
Q достигает максимума при

т.-е. при

Таким образом,
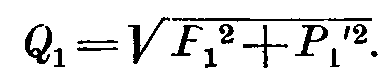
Выражение для Q принимает вид:
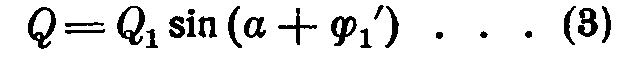
Угол 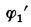 сдвига функции определим из выражений (2) и (3), подставляя
сдвига функции определим из выражений (2) и (3), подставляя  . Тогда
. Тогда
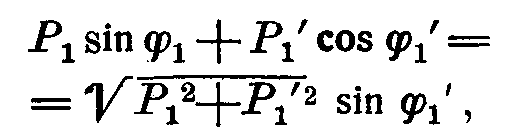
откуда
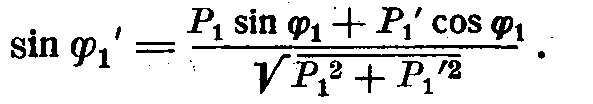
Для определения угла 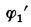 можно употреблять также и следующие выражения:
можно употреблять также и следующие выражения:
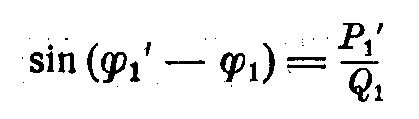
и
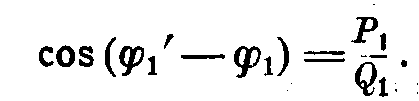
Таким образом, в зависимости от х0 или угла φ1, из данной сложной периодической кривой можно выделить любое количество гармонических кривых с различными амплитудами и с периодом, равным периоду данной кривой. Из этих гармоник необходимо отметить те, при которых P1, 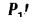 и Q1 являются максимальными для этой кривой.
и Q1 являются максимальными для этой кривой.
Как не трудно видеть, периодические силы кривой не поглощаются в каждый данный момент периодическими силами полученного нами гармонического колебательного движения того же периода. Остаточная кривая (фиг. 3), полученная после вычитания синусоиды Q из данной кривой, в состоянии в свою очередь вызвать колебательные движения с некоторыми другими периодами. Гармонические кривые этих колебательных движений определяются так же, как и первая гармоническая кривая с периодом t.
Определим гармоническую кривую с периодом, равным 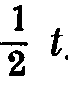 Для этого снова обратимся к кривой (фиг. 4) и разделим период t на четыре равные части. Представим себе, как и в первом случае, тело, вибрирующее под влиянием сил указанной кривой с периодом, равным
Для этого снова обратимся к кривой (фиг. 4) и разделим период t на четыре равные части. Представим себе, как и в первом случае, тело, вибрирующее под влиянием сил указанной кривой с периодом, равным 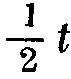 , при чем в течение первой и третьей четверти периода это тело колеблется в одну сторону от своего среднего положения, в течение второй и четвертой четверти - в сторону противоположную. Рассуждая так же, как и в первом случае, найдем, что в конце каждого периода t колебательное движение тела поглотит импульс сил, равный разности площадей
, при чем в течение первой и третьей четверти периода это тело колеблется в одну сторону от своего среднего положения, в течение второй и четвертой четверти - в сторону противоположную. Рассуждая так же, как и в первом случае, найдем, что в конце каждого периода t колебательное движение тела поглотит импульс сил, равный разности площадей
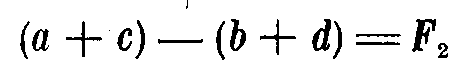
Полученная площадь F2 поглощается двумя полными колебаниями вибрирующего тела, т.-е. на каждое колебание приходится, таким образом, площадь, равная 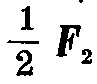 . Максимальное напряжение колеблющегося тела определится, как и в предыдущем случае, и будет равно:
. Максимальное напряжение колеблющегося тела определится, как и в предыдущем случае, и будет равно:

Полученная таким образом синусоида, с периодом 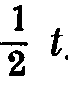 , будет:
, будет:
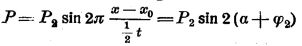
Сдвигая ординаты y1, y2, y3 и y4 на четверть периода этой синусоиды, получим другую разность площадей (фиг. 5)
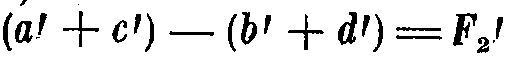 .
.
Эта площадь дает нам другую синусоиду, с периодом  , вида:
, вида:

Общий вид гармонической кривой с периодом  будет таким образом:
будет таким образом:
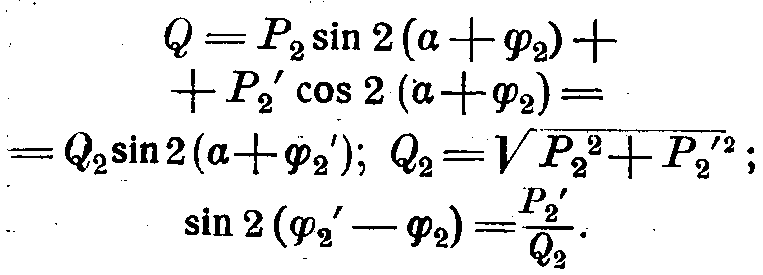
Рассуждая так же, как и в предыдущих случаях, определим составляющие гармонические кривые с периодами, равными:
 и т.д.
и т.д.
Во всех этих случаях найдем, что уравнение составляющей синусоиды для периода 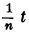 будет:
будет:
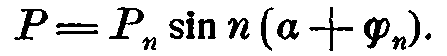
Для Р′ имеем
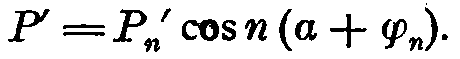
Общий вид гармонической кривой с периодом 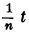 будет таким образом:
будет таким образом:
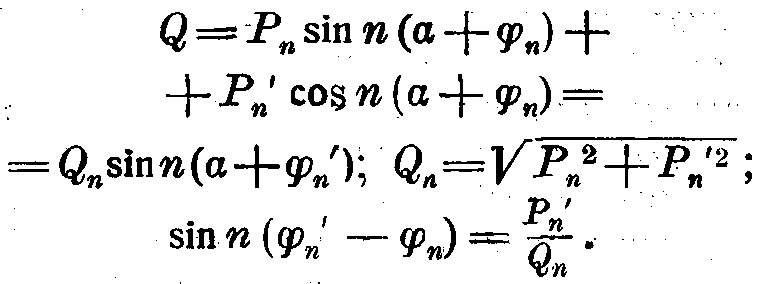
Таким образом определяются гармоники колебательных движений любого порядка, возникающие под действием сил, изменяющихся по закону данной сложной периодической кривой. Этим, однако, еще не определяются те гармоники, которые являются составляющими для данной сложной кривой, согласно ряда Фурье.
При определении этих составляющих необходимо учесть, то обстоятельство, что каждая из найденных гармоник колебательных движений какого-либо порядка составляется из гармоник того же порядка, умноженного на 1, 3, 5, 7 … и т.д., как в этом легко можно убедиться при помощи изложенного метода разложения кривых. Амплитуды этих составляющих равны соответственно этому  амплитуды данной составляющей.
амплитуды данной составляющей.
Напишем ряд Фурье для данной сложной периодической кривой в виде:
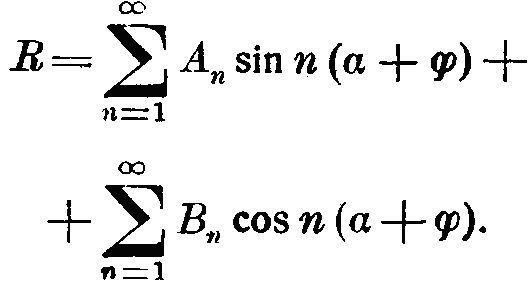
Тогда, как это следует из только - что изложенного:
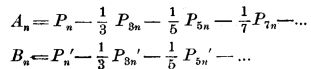
Таким образом, ряд Фурье для описываемой кривой напишется в виде:
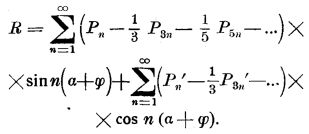
Здесь Р и Р′ являются соответствующими амплитудами тех колебательных движений, которые могут быть вызваны силами, изменяющимися по закону данной сложной периодической кривой.
Изложенный способ разложения сложных периодических кривых дает возможность быстро и с большой степенью точности находить как гармонические составляющие этих кривых, так и гармоники тех колебательных движений, которые могут возникнуть под действием сил, изменяющихся по закону данной сложной кривой.
В целях упрощения манипуляций, связанных с гармоническим анализом, на основании вышеизложенной теории этого анализа, предлагается аппарат, описание которого ниже следует.
На длинном стержне А насажено свободно вращающееся на шариках колесо В, катящееся по бумаге, на которой вычерчивается анализируемая периодическая кривая.
Последняя вычерчивается в полярных координатах, в центре которых укрепляется при помощи кнопок кольцеобразная шайба С. Период данной кривой принимается равным 2π или части этой величины.
Колесо В следует в своем движении за ведущей пластинкой D. Со стержнем А связан указатель Е с небольшой лупой F, на нижней поверхности которой наносится крест с точкой пересечения R. Стержень А не вращается, но имеет возможность свободно скользить в радиальном направлении, будучи поддерживаемым крестовиною G с осью H, дающей колесу В возможность свободно прижиматься к бумаге буртиком L. Крестовина G с осью H помещаются на стойке М, свободно вращающейся в отверстии кольцеобразной шайбы C и опирающейся своею подошвою на бумагу, на которой вычерчена исследуемая кривая.
На цилиндрической части колеса В нанесены деления, отсчитываемые при помощи простого штриха N или нониуса на ведущей пластинке D. Для обеспечения возможности следить за целыми числами оборотов колеса, на наружной поверхности его нарезается несколько ниток винтовой резьбы, в которой скользит штифтик Р тормоза Q. Последний служит также для удержания колеса В на месте без вращения, когда последнее поднимается от бумаги. Достигается это при помощи небольшой пружины, действующей на тормоз, как показано на чертеже.
Анализ исследуемой кривой, при помощи описанного прибора, производится следующим образом. Как показано на фиг. 9, шайба С прибора закрепляется в центре системы полярных координат, в которых вычерчена исследуемая кривая. Исследователь, взявшись руками за оба конца ведущей пластинки D и слегка прижимая колесо В к бумаге, обводит точкою R лупы исследуемую кривую. Колесо свободно катится по бумаге, проделывая в то же время некоторое скользящее движение в радиальном направлении в соответствии с формою обводимой кривой. После того, как точкою R будет обведена часть кривой, соответствующая половине периода исследуемого порядка, прибор останавливается, колесо поднимается от бумаги и точка R подводится к началу следующей нечетной части кривой, разделенной равными, углами на удвоенный порядковый номер исследуемой гармоники. Четная часть кривой пропускается, а следующая за ней нечетная часть обводится точкою R. Таким образом, обводятся все нечетные части кривой, при чем деления колеса В соответствующим образом суммируются. После этого, но уже в обратном направлении, отводятся все четные части кривой. Размеры колеса В выбираются такими, чтобы отсчитываемое в результате описанного действия деление колеса давало амплитуду соответствующей гармоники непосредственно в миллиметрах или в других единицах.
Теория этого прибора основана на вышеизложенной теории разложения периодических кривых на гармонические составляющие. Как не трудно видеть, прибор производит интегрирование выражений 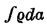 , что соответствует интегрированию выражений
, что соответствует интегрированию выражений 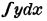 в прямоугольных координатах. Таким образом отсчитываемые на колесе В деления соответствуют площадям Fn и
в прямоугольных координатах. Таким образом отсчитываемые на колесе В деления соответствуют площадям Fn и 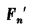 . Эти площади в свою очередь определяют амплитуды Pn и
. Эти площади в свою очередь определяют амплитуды Pn и 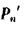 исследуемых гармоник.
исследуемых гармоник.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ВЫДЕЛЕНИЯ КОЛЛЕКТОРОВ В КАРБОНАТНЫХ ОТЛОЖЕНИЯХ | 1991 |
|
RU2014446C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ УРОВНЯ МОРЯ | 2011 |
|
RU2452984C1 |
| СПОСОБ АНАЛИЗА ТРЕНИЯ С ИСПОЛЬЗОВАНИЕМ АТОМНО-СИЛОВОЙ МИКРОСКОПИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2364855C1 |
| Устройство для анализа кривых переменного тока | 1932 |
|
SU41080A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЛЕБАНИЯ УРОВНЯ МОРЯ | 2005 |
|
RU2343415C2 |
| СПОСОБ ДИАГНОСТИКИ МЕХАНИЗМОВ И СИСТЕМ С ЭЛЕКТРИЧЕСКИМ ПРИВОДОМ | 2009 |
|
RU2431152C2 |
| СПОСОБ ПОВЫШЕНИЯ НЕФТЕОТДАЧИ МЕСТОРОЖДЕНИЯ И ДОБЫЧИ НЕФТИ | 2007 |
|
RU2347067C1 |
| СИСТЕМА СИНУСОИДАЛЬНОЙ ПЕРЕДАЧИ И СПОСОБ ФОТОТЕРАПИИ | 2019 |
|
RU2741471C2 |
| СИСТЕМА СИНУСОИДАЛЬНОЙ ПЕРЕДАЧИ И МЕТОД ФОТОТЕРАПИИ | 2021 |
|
RU2769423C1 |
| СИСТЕМА СИНУСОИДАЛЬНОЙ ПЕРЕДАЧИ И МЕТОД ФОТОТЕРАПИИ | 2015 |
|
RU2709115C2 |
Гармонический анализатор сложных, вычерченных в полярных координатах, периодических кривых, характеризущийся тем, что для отыскания амплитуды любой гармоники колебательных движений, выражаемых данною сложною периодическою кривою, используется пропорциональность амплитуды этой гармоники алгебраической сумме выражений 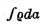 , попеременно взятых с положительным и отрицательным знаком за целый период и образуемых анализируемой кривой и двумя радиусами-векторами, отстоящими друг от друга на угол, соответствующий углу за полный период данной кривой, разделенному на удвоенный порядковый номер отыскиваемой гармоники, с каковой целью гармонический анализатор заключает в себе вертикальную поворотную стойку, при пользовании анализатором, приводимую в совпадение своим центром с центром координатной системы и поддерживающую длинный свободно скользящий в радиальном направлении стержень, расположенный над центром координатной системы и несущий на своем внешнем конце указатель для обвода кривой и свободно вращающееся колесо, вращательное движение которого при обводе кривой, сопряженное с радиальным перемещением стержня, интегрирует указанные выражения
, попеременно взятых с положительным и отрицательным знаком за целый период и образуемых анализируемой кривой и двумя радиусами-векторами, отстоящими друг от друга на угол, соответствующий углу за полный период данной кривой, разделенному на удвоенный порядковый номер отыскиваемой гармоники, с каковой целью гармонический анализатор заключает в себе вертикальную поворотную стойку, при пользовании анализатором, приводимую в совпадение своим центром с центром координатной системы и поддерживающую длинный свободно скользящий в радиальном направлении стержень, расположенный над центром координатной системы и несущий на своем внешнем конце указатель для обвода кривой и свободно вращающееся колесо, вращательное движение которого при обводе кривой, сопряженное с радиальным перемещением стержня, интегрирует указанные выражения 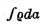 .
.
Авторы
Даты
1927-09-30—Публикация
1924-11-03—Подача