Изобретение относится к области морской гидрологии и может быть использовано для определения приливных колебаний уровня моря. Сущность: измеряют высоту поверхности уровня моря посредством регистрирующих устройств. Определяют момент верхней кульминации Луны на фиксированном географическом меридиане. Определяют колебания уровня моря путем анализа результатов наблюдений. При этом уровень моря измеряют в различных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом верхней кульминации Луны и моментом верхней кульминации Луны. Технический результат: снижение трудоемкости способа с одновременным повышением достоверности получаемых результатов.
Известные способы измерения уровня моря (Руководство по обработке и предсказанию приливов. - Л.: Гидрографическое управление ВМФ СССР. 1941, с.10 [1], Егоров Н.И., Безуглый И.М., Снежинский В.А. Морская гидрометеорология. - Л.: Управление гидрографической службы ВМФ. 1962, с.127-142 [2]) включают измерение уровня моря с использованием контактных измерителей, например мареографов (Правила гидрографической службы №35. Управление начальника гидрографической службы ВМФ. Л., 1956, с.39-43 [3]), или неконтактных (дистанционных) измерителей, например радиотехнических средств (Герман М.А. Спутниковая метрология. - Л.: Гидрометеоиздат. 1975, с.128-135 [4], Загородников А,А. Радиолокационная съемка морского волнения с летательных аппаратов. - Л.: Гидрометеоиздат, 1978, с.200-229 [5]), определение момента времени измерения, определение географических координат, определение момента верхней кульминации Луны на фиксированном географическом меридиане, например на гринвичском, определение колебания уровня моря путем анализа результатов наблюдений по периодическим компонентам во временных рядах результатов наблюдений с определением гармонических постоянных по всему спектру частот фиктивных светил (Дуванин А.И. Приливы в море. Гидрометеоиздат, 1960 [6], RU 2001106370 А, 20.05.2003 [7], ЕГОРОВ Н.И. Физическая океанография. - Л.: Гидрометеоиздат, 1966, стр.252-263 [8], US 6360599 B1, 26.03.2002 [9]).
Недостатком известных способов является то, что при определении колебания уровня моря в точке измерения используют зависимость изменения фазы видимого движения Солнца вокруг Земли, в то время как фазы колебаний уровня моря согласованы с фазами движения Луны вокруг Земли, а также существенная трудоемкость гармонического анализа прилива, по которому определяют высоту прилива. Так, например, формула для расчета высоты прилива при полном гармоническом анализе имеет 93 слагаемых (волн), что позволяет использовать его только для составления Таблиц приливов и в научно-исследовательских работах. Для практических целей, как правило, используется штурманский метод предвычисления приливов, который позволяет вычислять гармонические постоянные главных волн из наблюдений над колебаниями уровня за одни или двое суток и предвычислять приливы по гармоническим постоянным только четырех главных волн (Справочник вахтенного офицера. / Проничкин А.П., Чуприков М.К., Скворцов М.И. и др. - М.: Военное издательство МО СССР, 1975, с.300-302 [10], Справочник штурмана. / Каманин В.И., Емец К.А., Селитренников Г.В. и др. Под общей редакцией Шандабылова В.Д. - М.: Военное издательство МО СССР, 1968. с.382-391 [11]). Однако, чтобы учесть влияние этих волн, в амплитуды и фазы главных волн необходимо вводить поправки, которые зависят от астрономических условий. Кроме того, решение задачи преобразования интервалов времени основано на способах преобразования временных параметров исследуемых процессов, имеющих место при анализе результатов наблюдений (Полак И.Ф. Курс общей астрономии. - М.: ГИТТЛ. 1951 [12]). При этом на основе данных наблюдений для анализа результатов наблюдений выявляются периодические компоненты во временных рядах данных, для которых моменты измерения "асинхронны" с выявленным периодом колебаний, т.е. интервалы времени между моментами измерений не регулярны и значительно превышают выявляемый период колебаний, при этом используют Фурье-анализ, т.е. исследуемые процессы представляют как суперпозицию гармонических колебаний в виде ряда Фурье, что, например, при определении колебания уровня моря может вносить дополнительную погрешность, так как сумма двух периодических колебаний может быть непериодической функцией, например при сложении двух синусоидальных колебаний с несоизмеримыми частотами, когда в результате их сложения может быть получено сложное непериодическое колебание. При этом временной ход представляется в виде функций значений процесса от времени и время определяют из условия, что время есть строго возрастающая действительная переменная. При этом устанавливают структуру цикла временных интервалов с выделением эталона времени и выбирают цикловую частоту (Спилкер Д.Ж. Цифровая спутниковая связь. - М.: Связь, 1979, с.27, 254-255, 303-313, 467-474 [13], Дуванин А.И. Приливной год и системы времени // Вестник московского университета, сер.5. География, 1999, №2, с.8-13 [14], патент RU №2071104 [15]). Выбор цикловой частоты включает определение защитного временного интервала, обеспечение восстановления несущей, тактовую синхронизацию по элементам и адресацию информации, установление уровней сигналов во временных интервалах. Однако, ввиду того что периоды системы времени измерения и периоды гармоник колебательного процесса могут быть несоизмеримы, требуется выполнение дополнительных операций, связанных с обеспечением качественной синхронизации. При определении периодических компонент во временных рядах данных, полученных при наблюдениях за колебательным процессом, в котором моменты измерения являются асинхронными с выявленным периодом колебаний, используют свойство периодичности выявляемого сигнала па основе свойств периодической функции F(t+T)=f(t), где t - время; Т - период функции f(t). Для анализа гармонических колебаний ось времени разбивается на равные отрезки, которые в дальнейшем совмещаются друг с другом. В полученном таким образом циклическом времени моменты измерения описывают изменения функции на одном периоде, что обеспечивает связь между временем континентальным (солнечным) и океаническим (приливным) в соответствии с зависимостью х=y-ym, где х - приливное время (число приливных суток от начала приливного года); у - дата солнечного времени (число суток от начала года); ym - число суток между солнечным и приливным временем, т.е. при этом определяется среднесолнечное время, которое является циклическим временем с постоянным периодом в одни сутки. Связь между этими временами осуществляется путем развертки циклического среднего солнечного времени в линейный последовательный ряд путем введения пронумерованных временных интервалов: циклических - месяцев и нециклических - годов, столетий и т.д.
Однако, как известно (Полак И.Ф. Курс общей астрономии. - М.: ГИТТЛ, 1951 [12]), истинное солнечное время и истинные лунные сутки изменяют свою длительность в относительно широком диапазоне, что приводит к погрешностям при определении периодической составляющей в асинхронных гидрологических наблюдениях, обусловленных различием характера периодичности реального и измеренного процессов по причине измерения в циклической системе среднесолнечного времени. В то же время основные энергонесущие гармоники связаны с лунными периодами, вследствие чего периоды системы времени измерения и периоды гармоник процесса могут быть несоизмеримы. В этом случае в фазовом пространстве, построенном на несоизмеримых с процессом системы времени, траектории колебательного процесса ведут себя хаотически. В зависимости от размерности фазового пространства траектории могут носить квазипериодический характер с перемежаемостью и даже, более того, иметь структуру странного артефакта. Нестационарность процесса может быть также и следствием неэргодичности траекторий в фазовом пространстве.
Выявленных недостатков лишен известный способ определения колебания уровня моря (патент RU №2343415 С2 [16]), в котором технических результат, заключающийся в снижение трудоемкости определения колебания уровня моря с одновременным повышением достоверности определения конечных результатов, достигается тем, что измеряют высоту поверхности уровня моря посредством регистрирующих устройств. Определяют момент верхней кульминации Луны на фиксированном географическом меридиане. Определяют колебания уровня моря путем анализа результатов наблюдений. При этом уровень моря измеряют в различных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом верхней кульминации Луны и моментом верхней кульминации Луны.
В известном способе определение интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны позволяет определить временной ход приливных колебаний уровня в различных точках акватории моря и получить пространственный ход приливных колебаний на данной акватории на любой астрономический момент времени. Измеренные значения уровня моря в некоторых точках акватории моря, расположенных по возрастанию величины интервала времени позволяют по изменению фазы прилива определить и временной ход уровня в точке измерения под действием приливных сил. Ввиду того что колебательный процесс q уровня моря в каждый фиксированный момент времени будет являться функцией двух частот q(t)=q(ω0t, ωτt), а в каждый момент времени t значение колебательного процесса q(t) будет являться функцией двух независимых переменных: фазы φ0(t)=ω0t и фазы φτ(t)=ω0t, представляющих собой координаты фазового пространства, повышается вероятность достоверного выделения периодической составляющей колебательного процесса, так как исключается погрешность, обусловленная различным характером периодичности реального и измеренного колебательных процессов из-за измерения уровня моря в циклической системе среднесолнечного времени. При этом гармонические постоянные определяются на основании множества действительных чисел, в то время как в известных способах используются только рациональные числа, что позволяет определить реальную изменчивость колебательного процесса уровня моря.
Однако активизация технологического освоения континентального шельфа и прибрежной полосы морей повысила требования к точности и содержанию информации об уровне моря. Данные об уровне моря требуются при планировании и при оперативном обеспечении задач по добыче и транспортировке полезных ископаемых в прибрежных водах северных морей, при проектировании и строительстве портов и технических сооружений. Особую значимость эти данные имеют в задачах океанографического обеспечения так называемых морских операций - особо рискованных работах на море, например буксировка, установка и обеспечение функционирования плавучих буровых вышек.
Буксировку подобных объектов с большой осадкой в морях с приливами планируют на время наступления полной воды прилива с максимальными значениями относительно ближайших по времени. Такие приливы в океанографической практике связываются с явлениями новолуния и полнолуния (сизигиями) и называются сизигийными приливами. Среди серии последовательных сизигийных полных вод встречается вода с максимальной высотой за лунный месяц - период от одного новолуния до непосредственно последующего. Интервал времени от момента наступления новолуния до момента наступления прилива с максимальной полной водой называется возрастом прилива. Этот параметр приливов интересовал мореходов и исследователей со средних веков. Они отмечали, что в различных географических пунктах (портах) океана время наступления максимальной полной воды относительно момента наступления сизигии различно.
Это обстоятельство, в частности, Ньютон объясняет особенностями конкретных географических условий формирования прилива в данном месте (Ньютон И. Математические начала натуральной философии. - М.: Издательство ЛКИ. 2008. - 704 с. [17]).
Первоначально, до появления гармонического анализа приливов, понятие возраста прилива относилось к любому типу прилива (полусуточному, суточному и т.д.). С внедрением в практику гармонического анализа приливов единое понятие возраста прилива разделилось. Стали различать возраст прилива или возраст полусуточного прилива, возраст суточного прилива и возраст параллактического прилива.
Это условное деление можно объяснить недостаточной эффективностью используемых методов гармонического анализа приливов в начале XX века (Никитин М.В. Гармонический анализ приливов. - Л.: Гидрографическое Управление СССР. Гидро-Метеорологический отдел, 1925. - 168 с. [18]).
В настоящее время в отечественной и зарубежной практике (Tide and Current Glossary. - NOAA, National Ocean Service, 2000. - 34 р. [19], Вакман Д.Е., Вайнштейн Л.А. Амплитуда, фаза, частота - основные понятия теории колебаний // Успехи физических наук, том 123, вып.4, 1977, с.657-682 [20]) возраст прилива (age of tide = age of phase inequality) количественно выражается в часах среднесолнечного времени. Для вычисления возраста прилива используют выражение

Возраст суточного прилива (age of diurnal inequality) определяется выражением

а возраст параллактического прилива (ege of parallax inequality)

Здесь 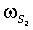 ,
, 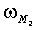 ,
, 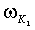 ,
, 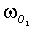 ,
, 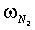 - угловые частоты (в градусах за час),
- угловые частоты (в градусах за час),  ,
, 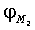 ,
, 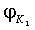 ,
, 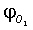 ,
, 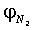 - фазы (в градусах) гармоник S2, М2, K1, O1, N2, соответственно. Отметим, что, во-первых, выражения (1-3) позволяют получить соответствующие возрасты прилива только для тех географических точек, для которых известны гармонические постоянные. Представление о географической (пространственной) изменчивости в морях времени наступления максимальных вод прилива после сизигий (возраста прилива) на основании этих выражений получить сложно. Например, можно предположить, что максимальная вода на акватории Белого моря наступает в один и тот же приливной цикл. Во-вторых, получаемые по выражениям (1-3) значения являются константами, т.е. интервал времени наступления, например, максимальной полной воды после любой сизигии постоянный и одинаковый для некоторой географической точки. Однако это не верно. Достаточно взять любые таблицы приливов и соответствующий астрономические ежегодник, чтобы выяснить, что максимальные воды после сизигий в одном и том же географическом пункте наступают через различные интервалы времени. Таким образом, можно констатировать, что в настоящее время задача океанографического обеспечения морских операций по проводке объектов с большой осадкой на критических глубинах на акватории с приливами не обеспечена падежной информацией о времени наступления сизигийных приливов.
- фазы (в градусах) гармоник S2, М2, K1, O1, N2, соответственно. Отметим, что, во-первых, выражения (1-3) позволяют получить соответствующие возрасты прилива только для тех географических точек, для которых известны гармонические постоянные. Представление о географической (пространственной) изменчивости в морях времени наступления максимальных вод прилива после сизигий (возраста прилива) на основании этих выражений получить сложно. Например, можно предположить, что максимальная вода на акватории Белого моря наступает в один и тот же приливной цикл. Во-вторых, получаемые по выражениям (1-3) значения являются константами, т.е. интервал времени наступления, например, максимальной полной воды после любой сизигии постоянный и одинаковый для некоторой географической точки. Однако это не верно. Достаточно взять любые таблицы приливов и соответствующий астрономические ежегодник, чтобы выяснить, что максимальные воды после сизигий в одном и том же географическом пункте наступают через различные интервалы времени. Таким образом, можно констатировать, что в настоящее время задача океанографического обеспечения морских операций по проводке объектов с большой осадкой на критических глубинах на акватории с приливами не обеспечена падежной информацией о времени наступления сизигийных приливов.
Задачей заявляемого технического решения является расширение функциональных возможностей способа определения колебания уровня моря.
Поставленная задача достигается за счет того, что в способе определения колебания уровня моря, включающем измерение высоты поверхности уровня моря посредством регистрирующих устройств, измерение моментов времени, определение верхней кульминации Луны на фиксированном географическом меридиане, определение колебания уровня моря путем анализа результатов наблюдений по периодическим компонентам во временных рядах результатов наблюдений с определением гармонических постоянных по спектру частот фиктивных светил, при анализе результатов измерений выполняют деление спектра частот на равные временные циклы с последующим их совмещением, в котором гармонические постоянные определяют для отдельного фиктивного светила, временной ход уровня прилива в точке измерения под действием приливных сил определяют по фазовому сдвигу, изменение фазы прилива определяют по измеренным значениям уровня моря в фиксированных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны, в котором в отличие от известного способа пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море определяют по изменению амплитуд гармонической составляющей высоты прилива со временем, при этом преобразования амплитуды, угловой частоты и фазы приливной гармоники по измеренным сигналам осуществляют путем интегрального и линейного преобразования Гильберта.
В основу заявляемого способа положены исследования, выполненные для прояснения ситуации с возрастом прилива. Для этого была исследована пространственно-временная изменчивость времени наступления максимальной полной воды после сизигий, как это понималось первоначально без разделения на типы прилива. Для этого было получено математическое выражение, обобщающее зависимости (1-3). В соответствии с гармоническим анализом приливов приливные колебания h(t) в точке представляются однородным гармоническим полиномом
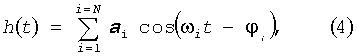
где t - среднесолнечное время, a i, ωi, φi - амплитуда, угловая частота и фаза приливной гармоники i (i=1, …, N). В (4) опущена астрономическая часть фаз для гармоник, чтобы не загромождать формулы элементами, не существенными для рассматриваемой задачи. Воспользуемся понятием аналитического сигнала [20] и представим (4) как действительную часть комплексной функции вида

где A(t) - мгновенная амплитуда, а Ф(t) - мгновенная фаза аналитического сигнала Z(t). Функции A(t) и Ф(t) называют огибающей и фазой Z(t). Из теории аналитического сигнала следует, что
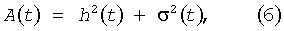
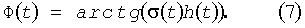
где σ(t) называется функцией сопряженной функции h(t) и определяется интегральным преобразованием Гильберта
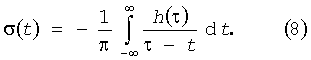
Для исследования возраста прилива достаточно рассмотреть только функцию А(t), так как Ф(t) имеет значительно большую частоту изменчивости. Именно огибающая A(t) описывает изменения амплитуды прилива со временем. Для получения явного выражения A(t) через параметры a i, ωi, φi воспользуемся линейным свойством преобразования Гильберта и тем, что для функции а·cos(ωt-φ) сопряженной функцией будет a·sin(ωt-φ).
Принимая во внимание, что при заданном N подкоренные члены в выражении (6) могут быть записаны в виде
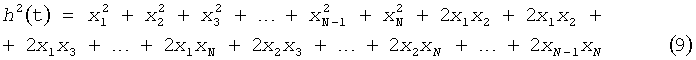 ,
,
где xi=a icos(ωit-φi), и учитывая, что выражение для σ2(t) будет аналогично (7), с xi=a isin(ωit-φi), получим для любого конечного N>=2
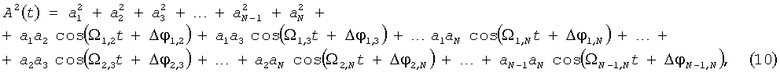
где Ωi,j=ωi-ωj, Δφi,j=φj-φi, i=1, …, N-1, j=2, …, N.
Заметим, что для N=2 из (9) следует, что
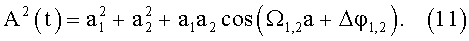
В этом случае максимум амплитуды будет наблюдаться при равенстве косинуса единице, то есть при t=Δφ2,1Ω1,2. Это в точности равно выражениям (1-3) для соответствующих гармоник.
Из выражения (9) следует, что огибающая имеет постоянную не зависящую от времени составляющую, определяемую амплитудами набора гармоник 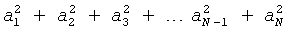 , и переменную, состоящую из элементов с косинусами. Частоты гармоник различны. Поэтому разности частот, входящие в косинусы (9), не равны между собой, и это приводит к смещению момента наступления максимального значения A(t) в последовательные интервалы между сизигиями.
, и переменную, состоящую из элементов с косинусами. Частоты гармоник различны. Поэтому разности частот, входящие в косинусы (9), не равны между собой, и это приводит к смещению момента наступления максимального значения A(t) в последовательные интервалы между сизигиями.
Рассмотрим скорость этого изменения. Для определенности ограничимся пятью основными гармониками, используемыми в (1-3): S2, М2, К1, O1, N2. Частоты этих гармоник выражаются через пять частот астрономических элементов [6]:
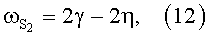
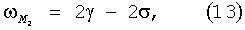

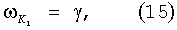
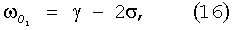 ,
,
где γ - угловая скорость вращения Земли (15.0410686390 град./час), σ - изменение средней долготы Луны (0.5490165304 град./час), η - изменение средней долготы Солнца (0.0410686390 град./час), ω - изменение средней долготы перигея Луны (0.0046418367 град./час).
Приведем все возможные частоты косинусов в (9) для этого набора гармоник:
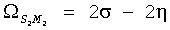 ,
, 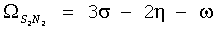 ,
, 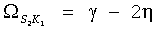 ,
,  ,
, 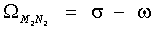 ,
, 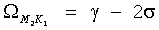 ,
, 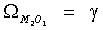 ,
,  ,
, 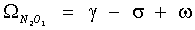 ,
,  .
.
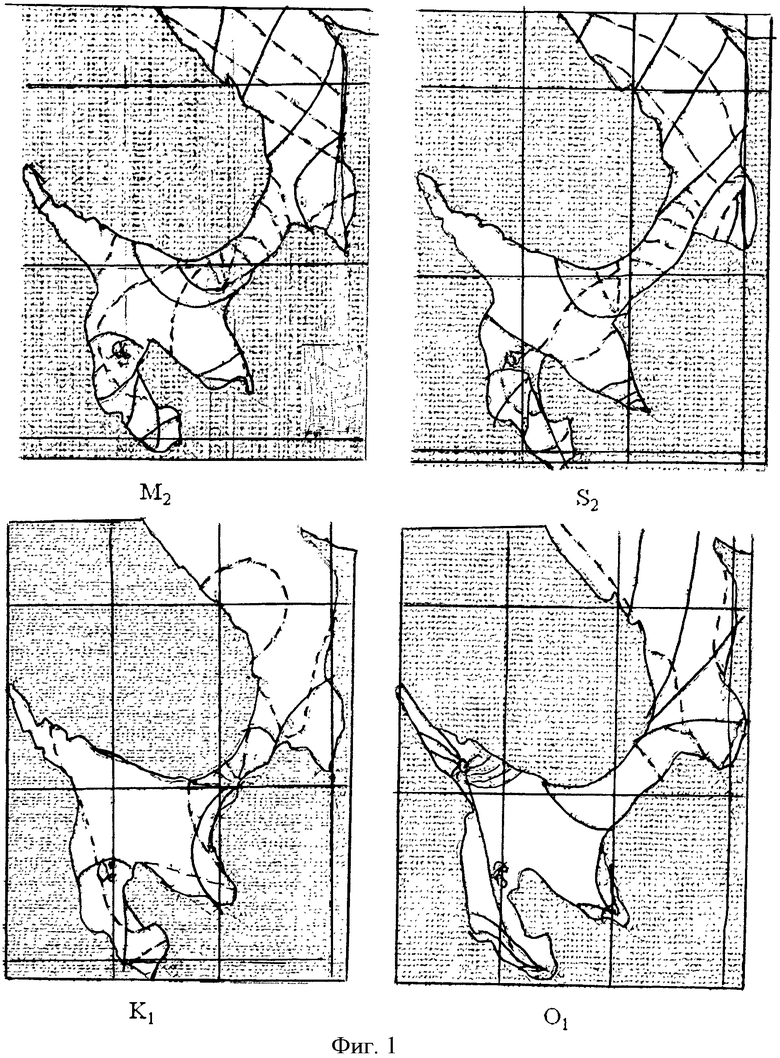
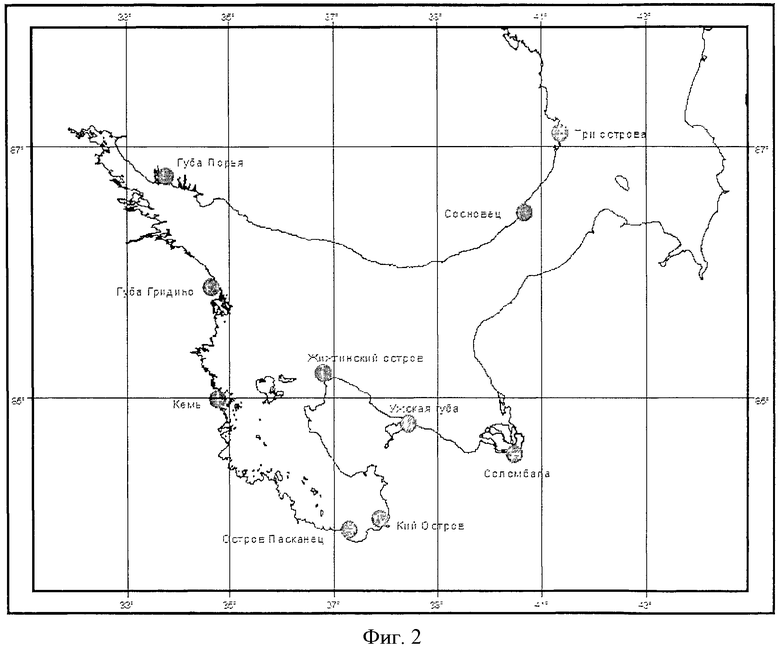
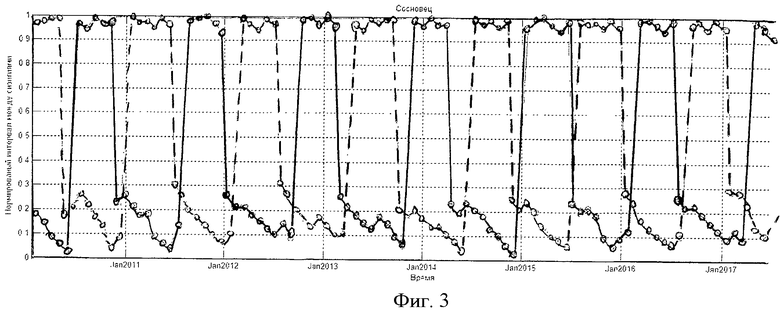
Учитывая, что γ>>σ>>η>>ω, можно утверждать, что огибающая имеет основную частоту вблизи значения 2σ. Кроме того, огибающая возмущается колебаниями с высокой частотой, близкой к γ. Для некоторых отношений амплитуд могут дополнительно возникать колебания с частотами, близкими к σ и 3σ. Основная частота изменчивости огибающей лежит вблизи 2σ. Это дает два максимума для огибающей за период в один лунный месяц. Наличие высокой частоты, близкой к γ, приводит к изменению наступления этих максимумов от месяца к месяцу. Это свидетельствует о некорректности выражений (1-3), которые дают постоянные значения возраста прилива. Изменение возраста прилива по акватории с использованием приливных карт или таблиц Приливов формально описать сложно. Причина этого в сложности распределения фаз гармонических постоянных по акватории и, что не менее важно, в различие их частот, что не дает явного способа «сложить картины» пространственного распределения отдельных гармоник. Для иллюстрации сложности распределения фаз гармонических постоянных на фиг.1 приведены приливные карты составляющих волн М2 (главная лунная полусуточная), S2 (главная солнечная полусуточная), K1 (лунно-солнечная суточная), O1 (главная лунная суточная) для акватории Белого моря. На фиг.1 (сплошные линии - инофазы, пунктирные - изоамплитуды) отчетливо видны области схождения изофаз - области амфидромических точек. В этих точках понятие фазы гармоники неопределенно, и выражения (1-3) теряют смысл, в то время как в (9) для этих точек можно формально приравнять нулю члены с соответствующей конкретной амфидромии гармоникой. Изменчивость возраста прилива по акваториям относительно велика. Действительно, период, соответствующий 2σ, приблизительно равен 327.9 среднесолнечных часов, а следовательно, изменение Δφ на один градус в соответствующем члене (9) приводит к смещению максимума почти на один час. Подтверждением этому служат результаты изменчивости возраста прилива по пространству, которые были получены путем прямого вычисления возраста прилива для конкретных пунктов по гармоническим постоянным. Такие вычисления были сделаны для десяти береговых пунктов Белого моря по наборам гармонических постоянных из базы IHO, Положение береговых пунктов приведено на фиг.2. В таблице 1 представлены расчеты возрастов приливов для этих пунктов, а на фиг.3 даны графики возраста прилива для пунктов «Три острова» и «Сосновец» на период с 2010 по 2018 гг. (1 - возраст прилива для больших сигизий, 2 - для малых).
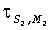

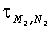
Таким образом, полученные результаты свидетельствуют, что наступление максимальных полных вод после сизигий в Белом море происходит в различные приливные циклы, а не в один.
Заявляемый способ реализуется следующим образом.
Посредством контактных или дистанционных измерителей уровня моря выполняют измерение уровня моря в различных точках акватории моря в различные моменты времени таким образом, чтобы получаемые измерения в каждой точке измерения имели различные значения интервалов времени относительно ближайшего к моменту измерения последнего момента верхней кульминации Луны на фиксированном географическом меридиане, аналогично, как и в прототипе [16].
При этом измеренные значения уровня моря в точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны на фиксированном меридиане и моментом измерения, позволяют установить временной ход уровня под действием приливных сил, что обусловлено тем, что приливные колебания в некоторой точке акватории моря имеют практически постоянный фазовый сдвиг относительно времени верхней кульминации Луны на фиксированном географическом меридиане. Так как сочетания фаз движения Луны вокруг Земли и фаз колебания уровня моря в некоторой точке повторяются с периодом движения Луны вокруг Земли, то измеренные значения уровня моря в некоторой точке акватории моря, расположенные по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны на фиксированном географическом меридиане и моментом измерения, представляют собой изменение фазы прилива, а следовательно, и временной ход уровня в точке измерения под действием приливных сил.
По измеренным приборным значениям уровня моря формируют ряды наблюдений. Определяют значения высоты прилива конкретной гармонической составляющей волны h(t), которая задается амплитудой А, углом положения g (А и g - гармонические постоянные) и периодом Т в соответствии с зависимостью h(t)=Acos(qt-g), где q - угловая скорость гармонической волны за один час среднего времени, t - фиксированный момент времени.
Определяют амплитуды гармонической составляющей высоты прилива.
Для анализа гармонических колебаний ось времени разбивается на равные отрезки, которые впоследствии совмещаются друг с другом. В полученном таким образом циклическом времени моменты измерения описывают изменения функции на одном периоде, что обеспечивает связь между временем континентальным (солнечным) и океаническим (приливным) в соответствии с зависимостью х=y-ym, где х - приливное время (число приливных суток от начала приливного года), у - дата солнечного времени (число суток от начала года), ym - число суток между солнечным и приливным временем (число суток от начала года). Вследствие того что периоды системы времени измерения и периоды гармоник колебательного процесса могут быть несоизмеримы, осуществляют преобразование циклического времени в линейное в соответствии с зависимостью r(t)=ωτt, где r(t) - циклическое время, t - линейное время, ωτ - частота циклической системы времени.
Далее выполняют дальнейшую обработку с учетом преобразованного времени. При этом колебательный процесс q в каждый фиксированный момент времени является функцией двух частот q(t)=q(ω0t, ωτt), а в каждый момент времени t значение колебательного процесса q(t) будет являться функцией двух независимых переменных: фазы φ0(t)=ω0t и фазы φτ(t)=ωτt, представляющих собой координаты фазового пространства.
Определяют значения высоты прилива h=h(x, у) для последовательного набора дискретных значений времени h=h(x, y, t), например, методом сеток (см., например, Лаврентьев М.А., Шабат Б.В. Методы теории функций переменного. - М-Л.: ГИТТЛ, 1958).
По полученным значениям высоты прилива для последовательного набора дискретных значений времени определяют амплитуды колебаний гармонической составляющей, например, в узлах сетки.
По полученным значениям h=h (x, y, t) определяют время наступления максимального уровня в пунктах измерения.
При обработке результатов измерений в соответствии с гармоническим анализом приливов приливные колебания h(t) в точке представляются однородным гармоническим полиномом
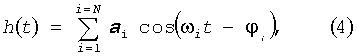
где t - среднесолнечное время, a i, ωi, φi - амплитуда, угловая частота и фаза приливной гармоники i(i=1,…,N). В соответствие с понятием аналитического сигнала [20] представляют (4) как действительную часть комплексной функции вида
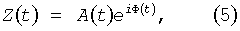
где A(t) - мгновенная амплитуда, а Ф(t) - мгновенная фаза аналитического сигнала Z(t), Функции A(t) и Ф(t) являются огибающей и фразой Z(t),
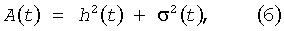
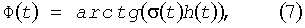
где σ(t) является функцией сопряженной функции h(t) и определяется интегральным преобразованием Гильберта
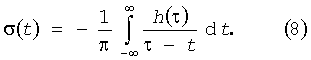
Для исследования возраста прилива рассматривают только функцию A(t), так как Ф(t) имеет значительно большую частоту изменчивости, а огибающая A(t) описывает изменения амплитуды прилива со временем. Для получения явного выражения А(t) через параметры a i, ωi, φi с учетом линейного свойства преобразования Гильберта и тем, что для функции а·cos(ωt-φ) сопряженной функцией будет а·sin(ωt-φ). Принимая во внимание, что при заданном N подкоренные члены в выражении (6) могут быть записаны в виде
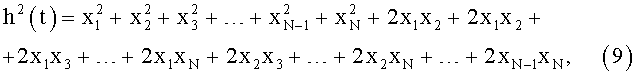
где xi=a·cos(ωit-φi), и учитывая, что выражение для σ2(t) будет аналогично (7), с xi=ai·sin(ωit-φi), получим для любого конечного N>=2
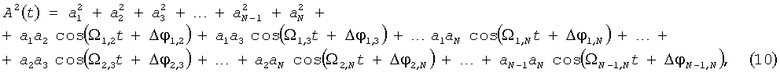 где Ωi,j=ωi-ωj, Δφi,j=φj-φi, i=1,…,N-1, j=2,…,N.
где Ωi,j=ωi-ωj, Δφi,j=φj-φi, i=1,…,N-1, j=2,…,N.
Заметим, что для N=2 из (9) следует, что
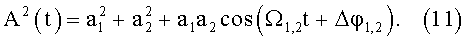
В этом случае максимум амплитуды будет наблюдаться при равенстве косинуса единице, то есть при t=Δφ2,1Ω1,2.
Из выражения (9) следует, что огибающая имеет постоянную не зависящую от времени составляющую, определяемую амплитудами набора гармоник 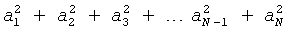 , и переменную, состоящую из элементов с косинусами. Частоты гармоник различны. Поэтому разности частот, входящие в косинусы (9), не равны между собой, и это приводит к смещению момента наступления максимального значения A(t) в последовательные интервалы между сизигиями.
, и переменную, состоящую из элементов с косинусами. Частоты гармоник различны. Поэтому разности частот, входящие в косинусы (9), не равны между собой, и это приводит к смещению момента наступления максимального значения A(t) в последовательные интервалы между сизигиями.
По смещению момента наступления максимального значения A(t) в последовательные интервалы между сизигиями определяют возраст прилива в точках открытого моря. При этом наличие высокой частоты, близкой к γ, приводит к изменению наступления этих максимумов от месяца к месяцу.
Предлагаемый способ выгодно отличается от известных способов, в которых регистрация приливов осуществляется в солнечном (циклическом) времени, что не обеспечивает информативность о повторяемости колебательного процесса, так как приливные колебания, записанные приборами в аномальном для их природы времени, оказываются зашифрованными для непосредственного анализа, что требует выражения результатов наблюдений рядами гармонических колебаний с аппроксимацией артефактов о реальной динамике приливных явлений, что может вносить дополнительные погрешности.
Применение заявляемого способа позволяет при анализе периодической составляющей колебательного процесса использовать множество действительных чисел, в то время как в известных способах, представляющих собой численные расчеты, используются только рациональные числа, что не позволяет определить реальную изменчивость колебательного процесса.
Кроме того, ввиду того что пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море определяют по изменению амплитуд гармонической составляющей высоты прилива со временем, при этом преобразования амплитуды, угловой частоты и фазы приливной гармоники измеренных сигналов осуществляют путем интегрального и линейного преобразований Гильберта, то обеспечивается возможность установления возраста прилива по пространству между стационарными пунктами измерения уровня моря, что существенно повышает океанографическое обеспечение проводки на мелководье плавучих объектов с большой осадкой.
Источники информации
1. Руководство по обработке и предсказанию приливов. - Л.: Гидрографическое управление ВМФ СССР. 1941, с.10.
2. Егоров Н.И., Безуглый И.М., Снежинский В.А. Морская гидрометеорология. - Л.: Управление гидрографической службы ВМФ. 1962, с.127-142.
3. Правила гидрографической службы №35. Управление начальника гидрографической службы ВМФ. Л., 1956, с.39-43.
4. Герман М.А. Спутниковая метрология. - Л.: Гидрометеоиздат.- 1975, с.128-135.
5. Загородников А.А, Радиолокационная съемка морского волнения с летательных аппаратов. - Л.: Гидрометеоиздат, 1978, с.200-229.
6. Дуванин А.И. Приливы в море. Гидрометеоиздат, 1960.
7. Заявка RU 2001106370 А, 20.05.2003.
8. Егоров Н.И. Физическая океанография. - Л.: Гидрометеоиздат, 1966, стр.252-263.
9. Патент US 6360599 B1, 26.03.2002.
10. Справочник вахтенного офицера. / Проничкин А.П., Чуприков М.К., Скворцов М.И. и др. - М.: Военное издательство МО СССР, 1975, с.300-302.
11. Справочник штурмана. / Каманин В.И., Емец К.А., Селитренников Г.В. и др. Под общей редакцией Шандабылова В.Д. - М.: Военное издательство МО СССР, 1968, с.382-391.
12. Полак И.Ф. Курс общей астрономии. - М.: ГИТТЛ, 1951.
13. Спилкер Д.Ж. Цифровая спутниковая связь. - М.: Связь, 1979, с.27, 254-255, 303-313, 467-474.
14. Дуванин А.И. Приливной год и системы времени // Вестник московского университета, сер.5. География, 1999, №2, с.8-13.
15. Патент RU №2071104.
16. Патент RU №2343415 С2.
17. Ньютон И. Математические начала натуральной философии. - М.: Издательство ЛКИ, 2008. - 704 с.
18. Никитин М.В. Гармонический анализ приливов. -Л.: Гидрографическое Управление СССР. Гидро-Метеорологический отдел, 1925. - 168 с.
19. Tide and Current Glossary. - NOAA, National Ocean Service, 2000. - 34 p.
20. Вакман Д.Е., Вайнштейн Л.А. Амплитуда, фаза, частота - основные понятия теории колебаний // Успехи физических наук, том 123, вып.4, 1977. - С.657-682.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЛЕБАНИЯ УРОВНЯ МОРЯ | 2012 |
|
RU2526490C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЛЕБАНИЯ УРОВНЯ МОРЯ | 2005 |
|
RU2343415C2 |
| СПОСОБ СОСТАВЛЕНИЯ ПРИЛИВНЫХ КАРТ | 2011 |
|
RU2450245C1 |
| СПОСОБ ПОВЫШЕНИЯ НЕФТЕОТДАЧИ МЕСТОРОЖДЕНИЯ И ДОБЫЧИ НЕФТИ | 2007 |
|
RU2347067C1 |
| СПОСОБ РЕГИСТРАЦИИ СЕЙСМИЧЕСКИХ СИГНАЛОВ НА АКВАТОРИИ МОРЯ ПРИ ПОИСКЕ ПОДВОДНЫХ ЗАЛЕЖЕЙ УГЛЕВОДОРОДОВ | 2011 |
|
RU2483330C1 |
| СПОСОБ МОРСКОЙ СЕЙСМИЧЕСКОЙ РАЗВЕДКИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2008 |
|
RU2388023C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ВОЗМОЖНОСТИ НАСТУПЛЕНИЯ КАТАСТРОФИЧЕСКИХ ЯВЛЕНИЙ | 2011 |
|
RU2489736C1 |
| СПОСОБ ПРОСТРАНСТВЕННОГО СОГЛАСОВАНИЯ ПРИЛИВНЫХ КОЛЕБАНИЙ ПРИ СОСТАВЛЕНИИ ПРИЛИВНЫХ КАРТ | 2015 |
|
RU2599913C2 |
| СПОСОБ ПОВЫШЕНИЯ НЕФТЕОТДАЧИ МЕСТОРОЖДЕНИЯ | 2012 |
|
RU2492316C1 |
| СПОСОБ ГИДРОМЕТЕОРОЛОГОАКУСТИЧЕСКОГО НАБЛЮДЕНИЯ ЗА АКВАТОРИЕЙ МОРСКОГО ПОЛИГОНА | 2005 |
|
RU2304794C2 |
Изобретение относится к области морской гидрологии и может быть использовано для определения приливных колебаний уровня моря. Сущность: измеряют высоту поверхности уровня моря посредством регистрирующих устройств. Определяют моменты верхней кульминации Луны на фиксированном географическом меридиане. Определяют колебания уровня моря путем анализа результатов наблюдений по периодическим компонентам во временных рядах. При этом определяют гармонические постоянные по спектру частот фиктивных светил. При анализе результатов измерений выполняют деление спектра частот на равные временные циклы с последующим их совмещением, в котором гармонические постоянные определяют для отдельного фиктивного светила. Временной ход уровня прилива в точке измерения под действием приливных сил определяют по фазовому сдвигу. Изменение фазы прилива определяют по измеренным значениям уровня моря в фиксированных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны. Кроме того, по изменению амплитуд гармонической составляющей высоты прилива со временем определяют пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море. При этом преобразования амплитуды, угловой частоты и фазы приливной гармоники сигналов осуществляют посредством интегрального и линейного преобразования Гильберта. Технический результат: расширение функциональных возможностей. 1 табл., 3 ил.
Способ определения колебания уровня моря, включающий измерение высоты поверхности уровня моря посредством регистрирующих устройств, измерение моментов времени, определение верхней кульминации Луны на фиксированном географическом меридиане, определение колебания уровня моря путем анализа результатов наблюдений по периодическим компонентам во временных рядах результатов наблюдений с определением гармонических постоянных по спектру частот фиктивных светил, при анализе результатов измерений выполняют деление спектра частот на равные временные циклы с последующим их совмещением, в котором гармонические постоянные определяют для отдельного фиктивного светила, временной ход уровня прилива в точке измерения под действием приливных сил определяют по фазовому сдвигу, изменение фазы прилива определяют по измеренным значениям уровня моря в фиксированных точках акватории моря, расположенных по возрастанию величины интервала времени между ближайшим предшествующим моментом времени верхней кульминации Луны и моментом верхней кульминации Луны, отличающийся тем, что пространственную изменчивость времени наступления максимальных вод прилива после сизигий в открытом море определяют по изменению амплитуд гармонической составляющей высоты прилива со временем, при этом преобразования амплитуды, угловой частоты и фазы приливной гармоники измеренных сигналов осуществляют путем интегрального и линейного преобразований Гильберта.
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЛЕБАНИЯ УРОВНЯ МОРЯ | 2005 |
|
RU2343415C2 |
| RU 2004134211 A, 10.05.2006 | |||
| RU 2001106370 A, 20.05.2003. | |||
Авторы
Даты
2012-06-10—Публикация
2011-01-20—Подача