Изобретение относится к счетному логарифмическому прибору в виде диска с нанесенными на нем многорядными шкалами и с радиальной огибающей обе стороны диска отсчетной линейкой, и заключается в том, что на отсчетной линейке помещены передвижные вдоль продольных прорезов в них индексные линейки, снабженные соответствующими шкалами и служащие совместно со шкалами на радиальных линейках для определения порядкового номера окруж ности, на которой следует производить отсчет результата произведенных дейстеий.
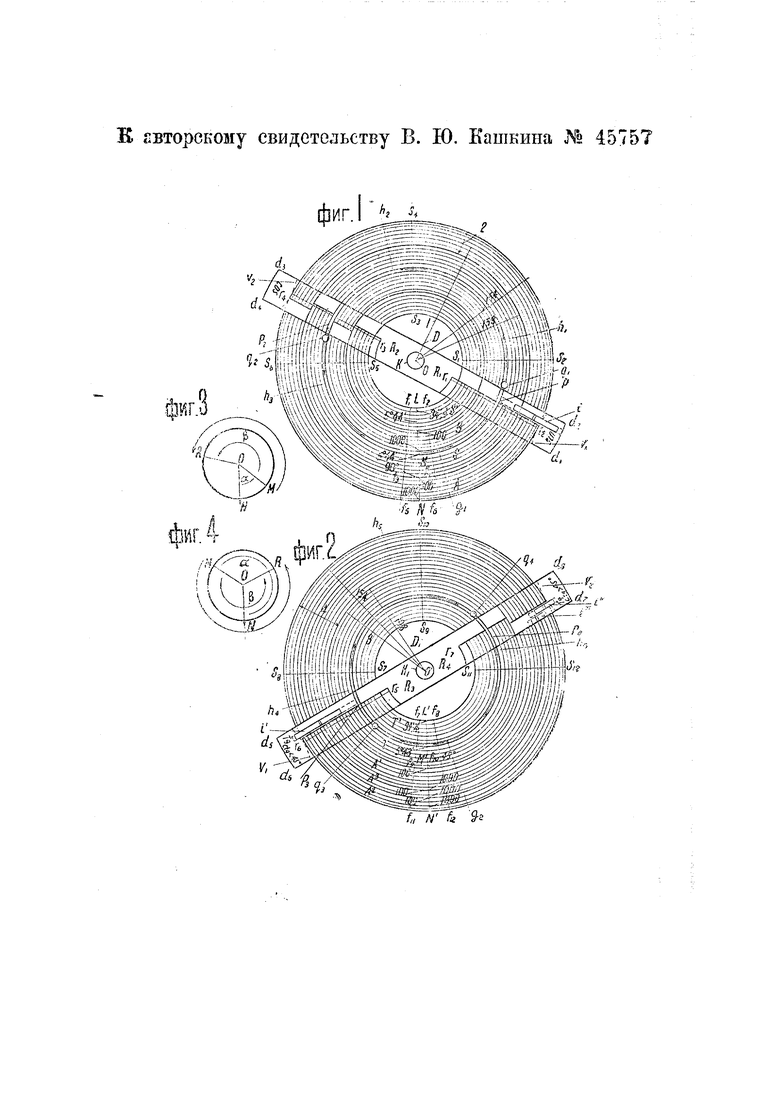
На чертеже фиг. 1 изображает вид прибора с передней стороны; фиг. 2- то же с задней стороны; фиг. 3 и 4 поясняют работу прибора; фиг. 5, 6, 7 8 изображают вид шкал на отсчетной линейке.
В приборе на передней поверхности (фиг. 1) счетного диска нанесены основные многорядные шкалы А и S и две шкалы синусов S и 5, одновременно являющиеся шкалами косинусов. Каждая из шкал нанесена на двенадцати концентрических окружностях, по обеим сторонам ряда графических окружностей.
Все шкалы представляют собой логарифмические шкалы чисел Л и S и логарифмов синусов 5 и 5 и наносятся обычным путем.
(136)
Деления на шкалах нанесены прртив часовой стрелки.
Внутренние шкалы S, В к S нанесены на подвижном диске /, который может вращаться в обе стороны на оси & относительно неподвижного внешнегб кольца 2; на последнем нанесена основ ная шкала логарифмов чисел Л.
На фиг. 1 внутренний подвижной диск / представлен установленным в своем начальном положении, т. е. его начальный радиус LM совмещен с начальным радиусом vVf/V неподвижного кольца 2.
Для отсчета делений на шкалах предназначена подвижная отсчетная линейка D, которая также может вращаться в обоих направлениях. Одну половину этой линейки можно обозначить, как визирный радиус с визирной нитью г, г, и другую половину, как визирный радиус с визирной нитью Гз, r.
Эти два радиуса визирной линейки несколько отличаются по своему устройству и назначению.
Приспособление i на визирном- радиусе представляет одну из индексных линеек прибора.
На обратной поверхности (фиг. 2) счетного диска нанесены оснор шкала чисел Л две шкалы,, сов 7 и Т, являющиеся одно
шкалами контангенсов, шкала каадратов /4 и шкала кубов А .
Внутренние шкалы Т и Т нанесены на подвижном писке 3, который может вращаться в обоих направлениях.
На внешнем неподвижном кольце 4 нанесена А , шкала квадратов А и шкала кубов Л . Шкала /l аналогична шкалам Л и В передней поверхности счетного дчска. Шкалы Л и Л отличаются своим масштабом, а именно, шкала А развернута на шести и шкала четырех шкаповых окружностях, нанесенных пэ обеим сторонам ряда графических окружносгей.
В отличие от шкалы передней поверхности все шкалы Л А-, А и шкалы Г и Р имеют основные численные обозначения, нанесенные по чэсовой сгрелке,т. е. в об,агном направлении ср 1виительно с передней поверхностью прибора.
Огсчетная линейка DI служит для отсчетов на шкалах обратной поверхности- Еа две полов1 ны или два визирных радиуса и / по своему выполнению и несомой функции несколько различаются между собой. По кромка1 1 и (l-ids Огсчетная линейка D,, наглухо соединена с краями (i,ii-i и отсчетной линейки D. Таким образом обе эти линейки составляют общий визирный диаметр ZJDj, который может вращаться на оси О - О, в обоих направлениях и предназначается для отсчетов на обеих поверхностях диска.
Визирный рздиус снабжен индексной линейкой i и визирный радиус снабжен двумя индексными линейками / и Г.
Имея две круговые логарифмические шкалы с общим центром и равными масштабами (модулями) и вращая одну из этих шкал, которую назовем подвижной, относительно другой, можно, как известно, осуществлять сложечиа и вычитание дуговых отрезков этх шкал, стягивающих углы, поопорциональные мантиссам логарифмов заданных чисел Лд, поскольку же на логарифмических Шкалах проставлены обозначения, отвечающие самим числам п, /, то очевидно можно этим путем непосредственно производить умножение и деление заданных чисел.
При построении таких приборов со шкалами, развернутыми на большом числе окружностей, необходимо предусмотреть способ нахождения той окружности, на которой должно прочесгь результат.
Зэдано например перемножить два числа «д и «. На диске (фиг. 1) находят множимое Яд на одной из 12 шкаловых окружносгей неподвижной шкалы А. Совмещают с найд нным мчожимым начальный радиус LM подвижного диска /. Находят тепе. на подвижном дискэ, на одной из 12 шкаловых окружностей шкалы В, зааанный миожитепь и сор,меи1ают с ним визирную нить г,Гз визирного радиуса. Поскольку этими действ, отложена сумма углов, представляющих мантиссы логар ф ов чисел Яд и п, то, очевидно, на пересечении продолжения установленной таким образом нити с одной из 12 окружностей неполвин ной шкалы Л можно прочитать искомое произведение.
Остается, следовательно, неопределенным, на какой именно окружности шкалы А должно искать произведение, отвечающее сумме углов, из которых каждый на диске может дэстигать 4320°.
Точно так же, при дгйс1вии деления остается неопределенным, на какой окружности неподвижной шкалы должно искать частное, отвечающее разности двух углов.
Рассматривая несколько подрэбнее происходящий при умножении процесс, видно, что угол срд. отвечающий множимому «д состоит из числа , полных окружностей и угла а, меньшего одной полной окружности т. е. где t 36Q.
Пусть угол «2,. отвечающий множителю л,, состоиг из числа k-, полных окружностей и угла , меньшего 350.
Складывая эти углы, имеем:
а - +
+
р„ + ,+Л. + .
Сумма и,-f-&, язпяя-ь цепых чисел, б/цег также целым чи:яом Сум.ча углон а-|-|3 можег колебаться между Q и 720, не достигая этих прзделов. При
, если сумма углов равна или больше 360°, получают еше одну дополнительную окрун-ность: а-|-р 360°-|-7 где if a-j-§ - 360° и, следовательно, не превышает ЗбОЛ Полагая, согласно принятому, 360° равным одной окружности, приходим к следующим двум О-новным случайм:
%H--f -(i + ) + « + -(О
где а -f р 360 и
% + -f/.-№ + .)4-f -(2)
где и представляет превышение суммы а-|- над 360.
Отметим злесь, что случаи (1) и (2) на поверхности счетного диска легко отличимы. Случай (1) представлен на фиг. 3 Нетрудно показать, что при (f, как представлено на этой фиг, дуга, проведенная по направлению шкал от подвижного радиуса ОМ до визирного радиуса OR, не пересечет не подвижного нача.1ьно1О радиуса ОЛ. Наоборот, если то при тех же условиях, как показано на фиг. 4, неподвижный радиус ОЛ пересекает дугу, проведенную от посвижного радиуса ОМ до визирного радиуса OR.
Число полных окружностей в сумме, согласно изложенному, может составлять . иJlи А,-| 2-j-l. При раз вертывании каждой из на М окружностей, ki л k-, в отдельности, очевидно, не превышают УИ-1; но сумма «X-J-1 может доходить до 2М - . Здесь мы имеем четыре случая:
, ... (I) 1 :S,-f Й--f-l Л1--1 . . {1Ь
, . . МП) ., . .(IV)
или при , как в диске:
0,+/fe,n .... (1)
1 и, + . . . (II)
12ssfe, . . . ()
,+i%2-f . . . (IVv
Случаи (1) и 00 имеют место, когда сумма полных окружностей в углах ср и p, не превышает Пи следовател1 но полная сумма не превышает 12 окружностей. Последнее будет иметь место, когда искомый результат (произведение га„ ffj не выходит за пределы основной шкалы.
Случаи (It) и (IV) качественно отличны от (1) и (11) и означают,, что результативный угол выходит за пределы 12 окружностей основной шкалы. Однако, как было сказано выше, основное свойство логарифмического счетного диска позволяет использовать повторяемость логарифмических шкал, условно рассматривая данную логарифмическую круговую шкалу, как ее продолжение. Начало этой второй шкалы А определится 12 ою и конец 24-ою полными окружностями.
Отсюда следует, что, вычитая Р случаях (ill) и (IV) из полученной суммы полных окружностей круговой модуль шкалы или 12, мы приведем условную вторую шкалу А к основной шкале, т. е. и в этих случаях найдем номер окружности шкалы А, на которой следует читать произведение.
Такое приведение влечет за собой важные преимущества и выполнимо в виду круговой формы шкал в сочетании с основным свойством повторяемости логарифмической функции для чисел, характеристики логарифмов которых разнятся на целое число единиц.
Из сказанного следует, что сложение любых углов концентрических круговых шкалах может производ;иться диференциональным путем, т. е. путем автоматического отделения на поверхности счетного диска наибольшего числа ft, и k- полных окружностей, заключающихся в этих углах, от углов а и р, представляющих остатки, и в последующем сложении чисел (или -|-/2 -}-1) и графическом сложении углов а и . Последнее производится вращением подвижного диска в пределах одного оборота, т. е. обычным iiyтем.
Сложение чисел полных окружностей при уменьщении, а также вычитание числа окружностей делителя из числа окружностей делимого при делении nfpoизводятся применением индексных -линеек прибора. При этом индексные линейки в случаях (111) и (IV) автоматически вычитают круговой модуль шкалы или 12, давая готовый уже приведенный к основной шкале результат.
Кроме того, индексные линейки определяют порядок результата и оэлегчаюг графическое сложение остаточных углов а и при умножении (соответственно вычитанию при делении).
Особую роль индексные линейки нэсут в автоматизации большого числа более сложных вычислений.
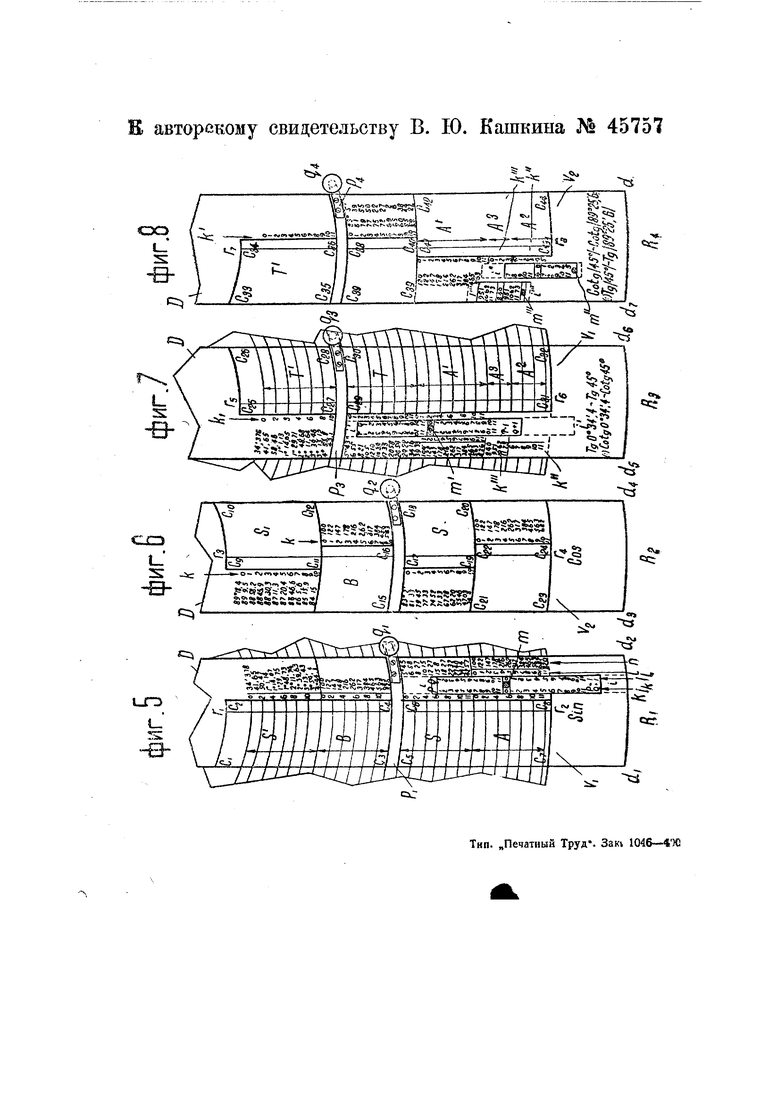
Оснзвной принцип индексных линеек сводится к перемещечиго, в направлении, перпендикулярном к линиям , ряда чисел, представляющих номера полных окружностей заданных углоз. На фиг. 5-8 представлена индексная линейка перед 1ей поверхности прибора.
Перенумеровав, как показано на фиг. 5 (столбец k) полные шчало ые окружности каждой из 4 шкал передней поверхности, поскольку число полньгх окружностей в угле равно пор дковому номеру окр/жности минус единица, полученные числа k будут возрастать от
0до 11.
Правее столбца k расположена индексная линейка и, которая может передвигаться в направлении, показанном пунктиром. При этом средняя линия Линейки перемещается в пределах неподвижной шкалы А или между числами ft 0 и k .
Столбец i линейки от линии О-О вниз повторяет числа столбца k. Отсюда следует, что, устанавливая среднюю ли«ию О-О индексной лингйки против заданной окружности (например k) шкалы А, прочитывают против любого Числа г линейки (вниз от О-0), число k полных окружностей в угле, равное Сумме чисел k и i.
чнсел i/ взерх от О-О построена иначе и дает сумму чисел k и г минус круговой модуль .1-12. С этой целью в столбце чисел / вверх рт О-О порядковые числа i всюду уве личены на 12, т. е. порядковое число
1заменено обозначением 11, порядковое число 2 заменено обозначением 10 и т. д. Нетрудно видеть, ч го при такой Системе числа 1 вверх от О-О приходите против чисеп k, равных суммэ k и jj минус 12 благодаря чему для случаев (III) и (IV) тоже может быть получен готовый результат.
Вторым основным следствием изложенной системы является то, что при любой установка индексной линейки численные обозначения в столбце /, приходящиеся против 12 ш аловых окружностей неаодвин ной щкалы /J, содержат полный ряД чисел от О до 11, на две части взгрх и вниз от О-О. Так, на линейке (фиг. 5) первую часть ряца находят вниз от О-О и вторую, начиная с верхней шка окружности шкалы // (числа 7-11).
Принимая те lepb во внимание, что числа k в пределах окружностей прибора непосредственно пэказызают числа полных окружностей в складываемых углах, получают, ч го, усганавливая линию О-О линейки против окружнос И .множимого ( А) и найдя число Zj на .индексной линийке, равное окружности множителя (шкалы S, В или S передней поверхности), можно во всрх четырех сл/чаях (I)-(iVj однообразным автоматизированным путем прочесть число полных окружностей результирующего угла.
При этом в сл/чаях (111) и (IV) прочитывается ргзуль1ат, уже автоматически приведенный к основной шкале Л.
Одночременио индексная линейка дает возможность определить порядок результаа.
Действительно, случаи (1) и (II) согласно определению означают, что сумма двух складываемых уг юа не превышает кругового модуля ш алы или 12 окружностей. После.гнее означает, что сумма мантисс л.гариф.мов двух сомножителей меньше 1, ч го, как известно, представляет случай, когда порядок произведения равен сумме сомножителей минус единица (символ Р-1).
Спучаи (111) и (IV) означают, что мантисс логарифмов даух сомножителей больше 1, или, что порядок произведения равен сумме сомножителей (символ Я).
Проставив теперь для части инд ксной линейки вверх от 0-0 символ Р и для другой части индексной линейки вниз от О-О Символ Я-1 получают возможность, совершенно так же, как на обычных логари4 мич скич линейках пользоваться этими o6j3Ha4eHHHMM дл
быстрого определения порядка произведения.
Аналогичным образом можно пока3atb, что символы Q и Q + l, назначение которых совпадаете тождественными си1 волами обычных счетных линеек, будучи проставлены на индексных линейках прибора, как показано на фиг. 7, позволяют определить порядок частного.
Предмет изобретения.
Счетный логарифмический прибор выполненный в виде диска с нанесен.
ными на нем многорядными логарифмическими шкалами и с радиальной, огибающей обе стороны диска отсчетной линейкой, отличающийся применением на отсчетных линейках передвижных, вдоль продольных прорезов в них, индексных линеек i, i, i, i, снабженных соответствующими шкалами и служащих совместно со шкалами на радиальных линейках для определения порядкового номера круга, на котором следует производить отсчет результата произведенных действий.
f, N f
.
Л,5с: 




| название | год | авторы | номер документа |
|---|---|---|---|
| Логарифмическая счетная линейка | 1956 |
|
SU117763A1 |
| СЧЕТНЫЙ ЛОГАРИФМИЧЕСКИЙ ПРИБОР | 1926 |
|
SU9392A1 |
| С четный логарифмический прибор | 1927 |
|
SU10447A1 |
| СЧЕТНАЯ ЛОГАРИФМИЧЕСКАЯ МАШИНА | 1931 |
|
SU37393A1 |
| Счетный логарифмический прибор | 1927 |
|
SU10545A1 |
| СЧЕТНЫЙ ЛОГАРИФМИЧЕСКИЙ ДИСК | 1923 |
|
SU3238A1 |
| Логарифмический счетный прибор | 1933 |
|
SU39446A1 |
| Счетный логарифмический диск | 1923 |
|
SU3354A1 |
| СЧЕТНЫЙ ЛОГАРИФМИЧЕСКИЙ ПРИБОР | 1928 |
|
SU9738A1 |
| Электрический счетный логарифмический прибор | 1935 |
|
SU44063A1 |


Авторы
Даты
1936-01-31—Публикация
1935-03-31—Подача