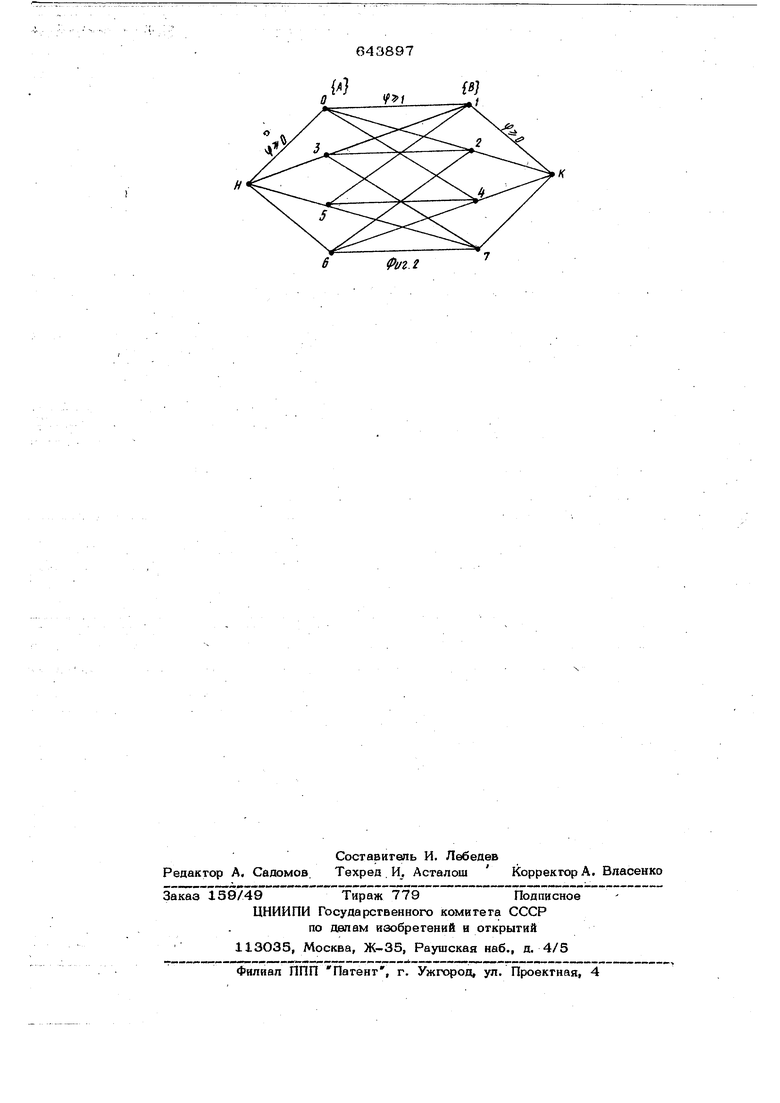
К первому входу соотвегствующего дополнигельного обратимого инвертора, подключенного вторым входом через соответствующий ограничивающий диод к соответствующему источнику опорного напряжения и через ключ к соответствующему входу выходного обратимого сумматора, П входов каждого из т дополнительных обратимых сумматоров подключены через ограничивающие диоды к соответствующим источникам опорньхх напряжений и через соответствующие обратимые инверторы и ключи - к одному из входов соответствующего основного обратимого сумматора. На фиг, 1 приведен упрощенный вариант схемы аналоговой модели для минимизации функции трех переменных; на фиг 2 показан граф функции. Модель (фиг. 1) состоит из обратимы сумматоров 1-.1О, обратимых инверторов 11-30, диодов 31-50, источников опорных напряжений 51-70, ключей 71-90, блоков индикации 91 и 92. Теоретическое обоснование аналоговой модели состоит в следующем. Задача определения оптимальной функции заключается в определении оптимального покрытия п -мерного куба, геометри чески отображающего функцию максимальными интервалами. Так как основной гра отображает функцию, то покрытием его назовем такое множество ребер, что любая вершина его служит граничной точкой хотя бы для одного из этих ребер. При этом наименьшее покрытие основного гра фа ябляется то, у которого множество ребер по абсолютной величине наименьше Очевидно, что задача нахождения наимень шего покрытия основного графа и задача определения оптимального покрытия 17 мерного куба максимальными интервалам эквивалентны. Наименьщее покрытие графа можно определить путем нахождения экстремальной величины потока в сети. Для этой цели положим, что булевая функция задана совершенной дизъюнктивной нормальной функцией и разобьем булевую функцию на два подмножества в одно из которых А входят конституенты с четным числом отрицательных переменных, в flpyroe Bj - нечетным, и построим граф, в котором соединены соседние конституенты из обеих подмножеств. Дополнив полученный граф булевой функции до расширенного введением источника Н и стока К (фиг. 2), положим, что пропускные способности реберНА {А е Ар иВЖ/В вГВЗ) больше или равны единице, а пропускные способности ребер равны или больше нуля. Тогда, если некоторую функцию (( поставить в соответствие количеству вещества, протекающего (в единицу времени) по ребру от Д кВ j , причем, если это коичество превышает пропускную способность ребра А Bj , то в {са-тдой вершине -ГЛ количество притекающего вещест ва равно количеству вытекающего. Число If выражает количество притекающего на выход К вещества и называется потоком. В случае, если величина потока (f S О определена множеством ребер сети и принимает целочисленное значение, то при наименьшем потоке ф ребра, для которых С О , обра;зуют наименьшее покрытие графа (см. фиг. 2). Следовательно, задача о наименьшем покрытии графа бул1евой функции является задачей о нахождении наименьшего потока в сети. Вариант модели, приведенной на фиг. 1, работает следующим образом. Функция, предназначенная для упрощения, представляется в виде двудольного графа, одни вершины которого соответствуют конституентам с чётным числом отрицательных переменных лЧ , а другиеконституентам единицы с нечетным числом отрицательных переменных Вд и набирается при помощи ключей 71-74 и 87-9О. Соседние конституенты единицы, отличающиеся одной переменной, соеди.иены через ключи 75.-86 ребрами. Основной граф дополнен до расширенного введением начальной Н и конечной К вершин (фиг. 2). В качестве моделей вершин графа используются обратимые сумматоры, а моделями ребер служат обратимые инверторы. Схема модели удовлетворяет соотношениям задачи о минимальном потоке, т.е. удовлетворяются принципы непрерывности и ограничения потока. Пля выходных сигналов -го сумма- . тора имеется зависимость 5:Ф; -1-Еч)я-о, где ф -величина потока, что соответствует .условию непрерывности потока. Ограничители напряжения диоды 31-50 и источ-, НИКИ опорных напряжений 51-7О) устанавливаются пропорционально пропускной спгсобности соответствующего ребра и моделируют зависимость ограничения потока в ребрах. Наличие обратимых инверторов 11-30 в каждом ребре вызвано необхояимосгью согласования знаков на ряжений. Ребра графа, по которым распрелелй я минимальный поток после набора гра фа функции ключами 75-86 отражают наименьшее покрытие графа, а значит сокращенную форму функции. Время опре деления наименьшего покрытия графа за висит от времени набора задачи и време ни переходных процессов схемы. В точках включения блоков индикации 91 и 92 устанавливаются напряжения, пропорциональные минимальному потоку. Использование аналогового принципа построения модели позволяет применять ранее не употребляемые для этих целей аналоговые решающие устройства, что существенно сокращает время решения задачи и повьшгает надежность ее решения,г Формула изобретения Аналоговая модель для минимизации булевых функций, содержащая источники опорных напряжений, ключи, ограничиваю щие диоды, выходной обратимый суммато к одному из входов которого подключен первый блок индикации, и г обратимых сумматоров, первые входы которых подключены через ограничивающие диоды к соответствующим п. источникам опорных напряже-тий и к первым входам п обратимых инверторов, подсоединенных вто- рымч входами через, соответствующие ключи к П входам вхошюго обратимого сумматора 7 (П + 1)-й вход которого соединен со вторым блоком индикации, о тличающаяся тем, что, с целью повБ шения б(з1стродействия мополи, она содержит дополнительные обратимые инверторы игл дополнительных обратимых сумматоров, один из входов каждого из которых подсоединен к первому входу соответствующего дополнительного обратимого инвертора, подключенного вторым входом через соответствующий ограничивающий диод к соот1зетствующему источнику опорного напряжения и через ключ к соответствующему входу выходного обратимого сумматора, ц входов каждого изШ дополнительн 11х обратимых сумматоров подключены через ограничивающие диоды к соответствующим источникам опорных напряжений и через соответствующие обратимые инверторы и ключи - к одному из входов соответствующего основного обратимого су гматора. Источники информации, принятые во внимание при экспертизе. 1. Авторское свидетельство СССР № 177692, кл. q 06 Р 15/34, 1964. 2. Тимошенко А. Г. Задача о максимальном потоке в сети и ее моделирование, сб. Специализированные электронные моделирующие машины и устройства, вып. АН УССР, К., 1967,. с. 19.
игг


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для определения маршрута максимальной пропускной способности исследуемой сети | 1985 |
|
SU1354201A1 |
| Устройство для определения максимального паросочетания в транспортных сетях | 1976 |
|
SU669360A1 |
| МОДЕЛИРУЮЩЕЕ УСТРОЙСТВО ДЛЯ ОПРЕДЕЛЕНИЯ НА ГРАФЕ ГАМИЛЬТОНОВА ЦИКЛА | 1971 |
|
SU304605A1 |
| Устройство для анализа параметров графа | 1988 |
|
SU1522229A1 |
| Устройство для определения экстремальных маршрутов | 1984 |
|
SU1193685A1 |
| Моделирующее устройство для определения статических и динамических характеристик синхронных машин | 1971 |
|
SU438996A1 |
| Устройство для анализа параметров сети | 1987 |
|
SU1474667A1 |
| Устройство для определения двух независимых кратчайших путей на графе | 1986 |
|
SU1336041A1 |
| Устройство для определения числа деревьев графа | 1973 |
|
SU485452A1 |
| Устройство для минмизации логических функций | 1974 |
|
SU558275A1 |



Авторы
Даты
1979-01-25—Публикация
1976-06-25—Подача