(54) СПОСОБ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ


| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ | 1993 |
|
RU2065170C1 |
| Способ определения разности фаз | 1988 |
|
SU1691772A1 |
| СПОСОБ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ СИГНАЛА | 1993 |
|
RU2090900C1 |
| Способ измерения нелинейных искажений | 1979 |
|
SU789885A1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛА | 1994 |
|
RU2086991C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛА | 1993 |
|
RU2065168C1 |
| Способ измерения нелинейных искажений | 1982 |
|
SU1020779A1 |
| Цифровой измеритель коэффициента нелинейных искажений | 1978 |
|
SU765745A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА НЕЛИНЕЙНОСТИ ХАРАКТЕРИСТИКИ ПАРАБОЛИЧЕСКОГО ВИДА НЕЛИНЕЙНОГО БЕЗЫНЕРЦИОННОГО ЭЛЕМЕНТА | 2001 |
|
RU2196337C1 |
| СПОСОБ ГАРМОНИЧЕСКОГО АНАЛИЗА СИГНАЛА | 1992 |
|
RU2010246C1 |

1
Изобретение относится к области ,электро- и радиоизмерений.
Известен способ измерения коэффициента нелинейных искажений, основанный на подавлении напряжения основ- 5 ной частоты jl. При таком способе с помощью заграждающего фильтра в исследуемом сигнале подавляют напряже-. ние первой гармоники и измеряют действующие значения исследуемого напря-«О жения и высших гармоник (без первой гармоники). Тогда коэффициент, нелинейных искажений определяют из выражения
.
где у - действующее значение высших.
гармоник исследуемого сигнала} У - действующее зна чение иссле- 20
дуемого сигнала. К недостаткам данного способа относится невысокая точность (несколько процентов)f недостаточный нижний предел измерения и ограничен- 25 ный частотный диапазон в сторону ншкних частот.
Иэвестен также способ измерения коэффициента нелинейных искеикений, основанный на измерении действующе-. 30
го значения первой и высших гармоник 2. В этом случае коэффициент искажений определяют согласно формуле
ч--(2.)
где у. - действующее значение первой гармоники.
Однако при дискретной реализации приходится иметь дело с разностью больших чисел. Известно, что в этом случае для обеспечения высокой точности вычислений необходимо сохранять определенное количество разрядов числовых значений Y и Y . Это приводит к значительным трудностям в схемной реализации способа. А любые возможные сбои в информационных разрядах чисел у и У приводят к увеличению погрешности.
Целью предлагаемого способа является повышение точности и упрощение аппаратурной реализации.
Цель достигается тем, что в способе измерения коэффициента нелинейных искажений, основанном на измерении коэффициентов Фурье основной гармоники, формируют два синусоидальных сигнала произвольной амплитуды, находящихся в квадратуре и
имеющих частоту исследуемого сигнала, измеряют приближенное значение дисперсии исследуемого сигнала отнйсительно суммы этих сигналов и постоянную составляющую исследуемого сигнала, вводятв приближенное значение дисперсии поправку, равную сумме квадратов постоянной составляющей и разности между каждым из измеренных коэффициентов Фурье и с амплитудой соотвеэствующёго синусоидального сигнала и по полученному значению дисперсии вычисляют коэффициент нелинейных искажений.
возможны различные варианты предлагаемого способа.
Рассмотрим дисперсию исследуемого сигнала f(t) относительно первой гармоники
т
D -- - (t)-As4h fa;it4 fdt, (4)
де f(t) - исследуемый периодический сигнал, период которого Т j
А и Ч - амплитуда и фаза первой гармоники сигнала f (t ) причем A-T/TY.
Выражение (4) можно записать слеующим образом
, тj
1 7rR( « o« -B5inuJt dl, (5 о
где C--Asih4,B AcosV- квадратурйые
составляющие амплитуды первой гармоники.
Раскрывая скобки в .выражении (4), получим
В- )at-2A 7Ji(U5w()at + о °
()dt. - о . .
Так как
flf iWi-Y,
4 И(t)вin()dt --А -- VTVi, о
f.(«;t.f)) f ,
что совпадает с выражением(З).т.е. .
Таким образом, коэффициент нелинейных искажений действительно может быть определен по дисперсии О исследуемого сигнала f(t) относительно первой гармоники.
Первая гармоника может быть либо вьвделена из исследуемого сигнала, либо сформирована или непосредственно Л sin (UJi-t-V), или как сумма двух гармонических сигналов Ссов iw-fc .и Bs-intut , находящихся в квадратуре. Вьщеление первой гармоники из исследуемого сигнала
связано с использованием фильтров,
что приводит к недостаткам известных способов. Этих Недостатков можно избежать-, если предварительно измерить параметры первой гармоники (либо А и f либо 8 и С), и по
этим параметрам сформировать образцовую первую- гармонику. Для измерения указанных параметров наиболее целесообразно использовать цифровые методы, обеспечивающие значительное
повышение точности и расширение ,частотного диапазона в область нижних частот.
Предлагаемый способ также целесообразно реализовать в цифровой фор-.
ме, при которой соотношения (4) и (5) имеют вид
D- s UiVA5in(ujt;i-vv)f, (ь) D J s(t,)-Ccosiwt--Bsihujt, (7)
где f(ii) - мгновенные значения исследуемого сигнала в точках дискретизации )
N - число точек дискретиза/
Злщкг,)f -дискретные значения Sin wi -jCoswii синусоидальных функ ций в точках дискретизации .
Параметры первой гармоники определяются следующими выражениями:
А-- }7 2 (ti)sin{twt,-h4),
1-Б- | S(t.,biviuut
1 12 N
С 2 f (tiOcosujt,-. i-1
Таким образом, при определении параметров первой гармоники и величины участвуют одни и те же величины f((tУti Ч),,.i. что, естественно, является благоприятным фактором при реализации способа.
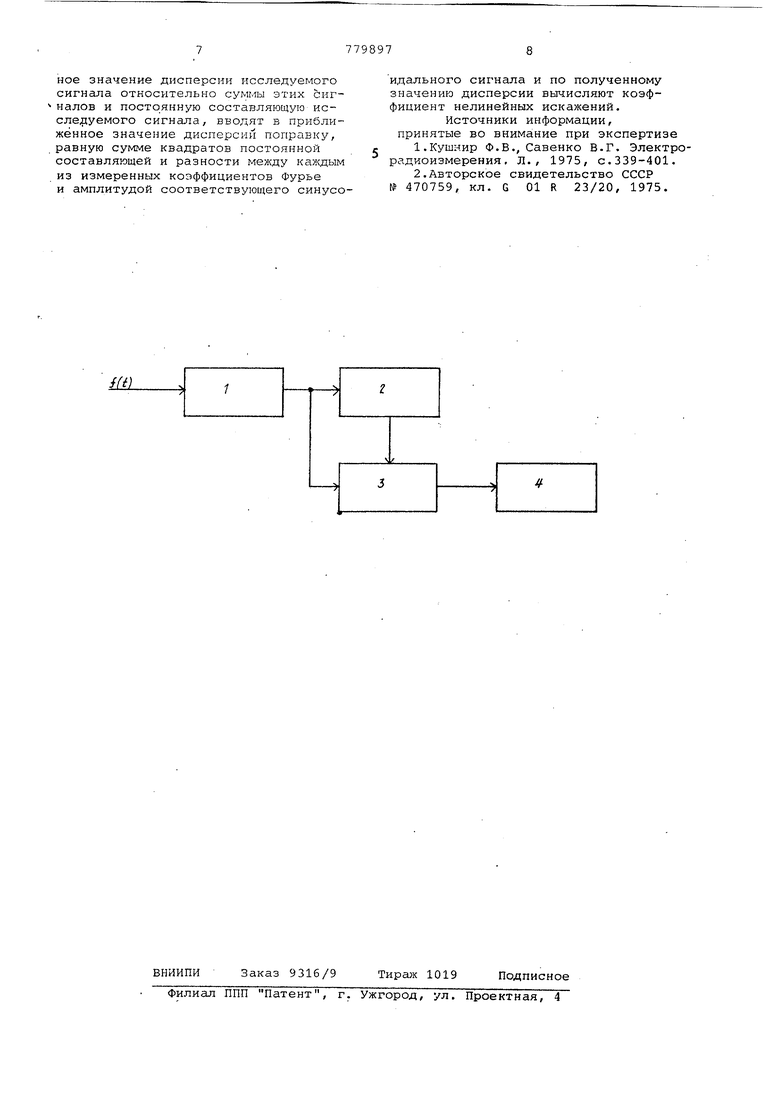
Можно указать еще один вариант предлагаемого- способа. Состоит он в следующем. Если вначале задать ::я приближенно величинами В и С, например, в, и Со г и относительно гармонического сигнала с такими паоаметрами определить приближенное значение дисперсии В исследуемо го сигнала Б-- (iiVC C05U;ti-BoSincwi f, (8) то оказывается, что такое значение, дисперсии связано с приближенным соотношением в--Ъ--|(), где й В-В-Во,. . Это означает, что приближенное значение дисперсии Т5 необходимо уточнить путем введения поправок, .обусловленных уточнением величин 6 и С. Такой вариант способа позволяе увеличить быстродействие измерений по сравнению с ра:ссмотренными выше двумя вариантами, так как в нем йёт необходимости предварительно 1очно измерять параметры первой гармоники Они могут быть либо измерены достаточно приближенно, либо задана. Если в исследуемом сигнале есть постоянная составляющая f , то дисперсию следует определять из выражения D - Ij- UiVioCQCostwi-BQUWuu-b -(i Urf/b-bf-vf cfl -(.ь)%(с) где f - приближённое значение посто янной составляющей. Преимущества предлагаемого способа в простоте аппаратурной реализации, в большей точности, обеспечиваемой меньшими возможностями сбоев. Вычисления проводятся с такой точностью, чтобы не загрублять точность входных данных. Здесь., однако, следует собл 1одать меру, ибо погоня за очень высокой Точностью вычислений приводит к чрезмерному увеличению объема перерабатываемой информации без существенного повышения точности окончательного резул тата. Кроме того, это приводит к ус ложнению схемной реализации способа При цифровом варианте способа возрастают разрядности, счетных узлов, а это увеличивает вероятность сбое и погрешность измерений. При вычислениях необходимо иметь в запасе один, максимум два разряд которые в окончательном результате следует округлять. Преимущества более наглядны на цифровом варианте способа. Пусть погрешность измерения мгновенных з чений i5f- . Тогда необходимая разрядность числа {(-t.-) , а, с;педова тельно, и разрядность десятичного счетчика, в который это число поступает:--Щ- а объем счетчика . С такой же . точностью следует вычислять и величины В и С. Что касается точности, с которой следует возводить в квадрат, и объема счетчика, в котором накапливаются квадраты, то она будет разной для противопоставляемого и предлагаемого способов. В предлагаемом способе, как следует из выражения (5), объем счетчика квадратов равен ( f ). а его разрядность Ум:j-vyii-2C lkn. В противопоставляемом способе, как следует из выражения (3), разрядность величин (и счетчика квадратов) ш2 -г 2т . При не очень малых К у, это не очень существенно, но для малых Kyj может быть весьма существенным. Например, при К, 0,1% это дает б лишних десятичных разряЯОВСуть предлагаемого способа поясняется структурной схемой устройства, приведенной ла чертеже. В состав устройства, входят: измеритель 1 параметров гармоники, формирователь 2 первой гармоники, измеритель дисперсии 3, блок вычисления 4. Измерение коэффициента нелинейных искажений производится следующим образом. Вначале ис.следуемый сигнал f{t) поступает на измеритель 1, которым производится определение параметров первой гармоники А и S или В и С. П6лs eнныe значения этих параметров вводятся в формирователь первой гармоники. Если реализуется соотношение (9), то параметры BQH Со вводятся сразу в формирователь 2.. После этого исследуемый сигнал и сформированная гармоника сигнала поступают в измеритель дисперсии 3. Измеренное значение дисперсии исследуемого сигнала относительно первой гармоники вводится в блок вычисления 4, в котором пб дисперсии находят коэффициент искажений. Формула изо.бретения Способ измерения коэффициента нелинейных искажений, основанный на измерении коэффициентов Фурье основной гармоники, отличающийс я тем, что, с целью повышения точности и расширения частотного диапазона в сторону низких частот, формируют два синусоидальных.сигнала произвольной амплитуды, находящихся в квадратуре и имеющих частоту исследуемого сигнала, измеряют приближен.л
ное значение дисперсии исследуемого сигнала относительно суммы этих сигналов и постоянную составляющую иссле 1уемого сигнала, вво/лят в приближённое значение дисперсий поправку, равную сумме квадратов постоянной составляющей и разности между каждым из измеренных коэффициентов Фурье и амплитудой соответствующего синусоидального сигнала и по полученному значению дисперсии вычисляют коэффициент нелинейных искажений.
Источники информации, принятые во внимание при экспертизе

Авторы
Даты
1980-11-15—Публикация
1978-02-17—Подача