(54) ФУНКЦИОНАЛЬНШ ПРЕОБРАЗОВАТЕЛЬ



| название | год | авторы | номер документа |
|---|---|---|---|
| Функциональный преобразователь | 1981 |
|
SU955113A1 |
| Функциональный преобразователь | 1980 |
|
SU934502A1 |
| Функциональный преобразователь | 1981 |
|
SU962996A1 |
| Аппроксимирующий функциональный преобразователь | 1983 |
|
SU1104542A1 |
| Устройство для формирования ординат эллипса | 1980 |
|
SU1003107A1 |
| Функциональный преобразователь двух переменных | 1983 |
|
SU1109766A1 |
| Устройство для формирования функции эллипса | 1983 |
|
SU1133600A1 |
| Логарифмический преобразователь | 1979 |
|
SU790003A1 |
| Функциональный преобразователь | 1983 |
|
SU1137488A1 |
| Кусочно-нелинейный функциональный преобразователь | 1988 |
|
SU1562940A1 |


Изобретение относится к аналоговой вычислительной технике. Известен функциональный преобразователь, содержащий диодные ограни тели, инвертор тока, выходной сумматор, источник опорного напряжения который осуществляет кусочно-линейную аппроксимацию функций 1. Его недостатком является наличие методической погрешности обусловленной способом аппроксимации воспроизводимой функции. Наиболее близок к предложенному функциональный преобразователь , содержащий источник синусоидального напряжения, сумматор, фазовращатель включенный между выходом источника синусоидального напряжения и первым входом сумматора, амплитудный модулятор, информационный вход которого соединен с выходом источника синусо идального напряжения, выход - со втоЕЯЛм входом сумматора, а управляющий вход является входом преобразо вателя, блок преобразования напряже ния в фазу, включенный между выходом источника синусоидального сигнала и третьим входом сумматора, вы ход которого подключен к первому входу блока сравнени.я, соединенного выходом с управляющим входом блока преобразования напряжения в фазу, а вторым входом - с выходом источника синусоидального сигнала 2. Этот функциональный преобразователь не позволяет осуществлять точное (без методической погрешности) воспроизведение центральных кривых второго порядка с осями, параллельными осям координат, и реализовать аппроксимацию других нелинейных зависимостей указанными центральными кривыми. Цель изобретения - расширение класса решаемых задач и повьлиение точности работы преобразователя. Поставленная цель достигается тем что функциональный преобразователь, содержащий блок сравнения, источник синусоидального напряжения, сумматор, фазовращатель, вк.гиоченный между выходом источника синусоидального напряжения и первым входом сумматора, амплитудный модулятор, информационный вход которого соединен с выходом источника синусоидального напряжения, а выход - со вторым входом суквдатора, дополнительно, содержит блок масштабного преобразования, два линейных выпрямителя, два фильтра
нижних частот, дополнительные блок сравнения и амплитудный модулятор, информационный вход которого подключен к выходу фазовращателя, управлякядий вход - к выходу основного блока сравнения, а выход - ко входу блока масштабного преобразования, и треть ему входу сумматора, выход сумматора через последовательно соединенные первый линейный выпрямитель и первый фильтр нижних частот соединен с первым входом основного блока сравнения, второй вход которого соединен с шиной опорного напряжения, выход основного амплитудного мод;улятора через последовательно соединенные втрой линейный -выпрямитель и второй фильтр нижних частот соединен с первым входом дополнительного блока сравнения, выход которого подключен к управляющему входу основного амплитудного модулятора, а второй вход является входом преобразователя, выход источника синусоидального напряжения соединен с четвертым входом сумматора.
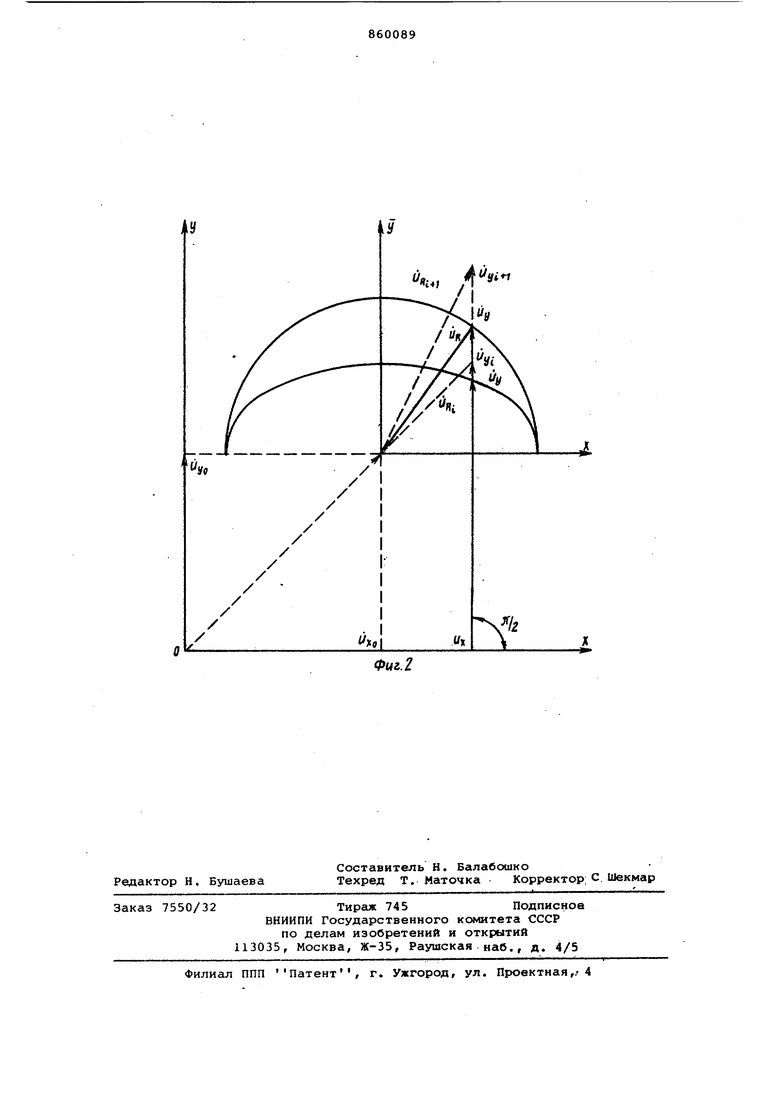
На фиг. 1 представлена блок-схема функционального преобразователя; на фиг. 2 - векторная диаграмма напряжений, поясняющая его работу.
Преобразователь содержит источник 1 синусоидального напряжения, фазовращатель 2, основной 3 и дополнительный 4 амплитудные модуляторы, сумматор -5, блок б масштабного преобразования, первый 7 и второй 8 линейные выпрямители, первый 9 и второй 10 фильтры нижних частот, основной 1 и дополнительный 12 блоки сравнения.
Работа функционального преобразователя основана на реализации алгоритма, полученного путем использования аффинного преобразования, и приме 1ении векторно-электрического метода.
Запишем каноническое уравнение эллипса
---1, Н)
где Uv/U - напряжения, величина которых пропорциональна зависимой у и независимой X переменным, связанных уравнением эллипса;
U, напряжения, величина которых пропорциональна малой b и большой а осям эллипса.
Уравнение (1) может быть преобразовано к виду
.
где К и. /и - коэффициент аффинно го подобия;
напряжение, пропорциональное по величине ординате окружности с радиусом, равным U Из уравнения (2) видно, что эллипс можно моделировать с помощью окружности-, аффинно подобной воспроизводимому эллипсу с радиусом, равньлм большой оси эллипса U и последующим изменением полученного напряжения U,y , пропорционального ординате окружности, на величину коэффициента аффинного подобия KQ. Уравнение (2) позволяет моделировать эллипс в системе координат, совпадающей с осями эллипса. Для воспроизведения эллипса в системе координат ХОУ/ не совпадающей с осями эллипса ХОУ, необходимо ввести два дополнительных напряжения UyQ, сдвинутых по фазе на и определяющих положение центра моделируемой окружности (фиг. 2). Так как аффинное преобразование должно производиться только с напряжением и , пропорциональным ординате окружности и в собственной системе координат ХОУ, то величина напряжения должна определяться с учетом коэффициента аффинного подобия. Это достигается изменением й на величину К по отношению к напряжению , пропорциональному ординате центра моделируемого эллипса. При таком выборе величины напряжения Ьу изменение величины напряжения й на величину К а приводит к выполнению уравнения (2):
,--K(), W
де U- - напряжение, величина которо о пропорциональна ординате окружности в CHCTeivue координат ХОУ;
UYO
Vнапряжение, величина которого пропорциональна ординате центра моделируемой окружности;
(
и
напряжение, величина
VO которого пропорциональна ординате центра моделируемого эллипса;
К и
напряжение, величина а S которого пропорциональна ординате эллипса в собственной системе координат ХОУ. Из уравнения ) видно, что велиина напряжения ulj пропорциональна рдинате эллипса в системе коордиат ХОУ.
Функциональный преобразователь раотает следующим образом.
Напряжение Up с выхода источниа 1 синусоидального напряжения поступает на входы фазовращателя 2, сумматора 5 и амплитудного модулятора 3. Напряжение с выхода фазовращателя 2, сдвинутое по фазе на 1t/2 относительно напряжения источника 1 синусоидального напряжения, поступает на информационный вход амплитудного мфдулятора 4 и первый вход сумматора 5. Изменяя коэффициент передачи сумматора 5 по каждому из входов, устанавливают напряжение по первому входу й , пропорциональ,ное по величине абсциссе центра воспроизводимой окружности, а по четвертому - напряжение UVQ / пропорциональное по величине ординате центра воспроизводимой окружности. На второй вход сумматора 5 поступает напряжение с выхода амплитудного модулятора 3, на информационный входа которого подается напряжение с выхода источника 1 синусоидального напряжения, а на управляющий вход - напряжение с выхода блока 12 сравнения. На один из входов блока 12 сравнения поступает напряжение с выхода амплитудного модулятора 3, через линейный выпрямитель 8 и фильтр 10 низших частот, а на другой - напряжение входного сигнала. При равенстве значений указанных напряжений амплитудного модулятора 3 устанавливается синусоидальное напряжение 6,, пропорциональное по величине входному сигналу.
На третий вход сумматора 5 поступает напряжение U,, с выхода амплитудного модулятора 4, в,общем случае равное по величине и или Uy Напряжение на выходе сумМатора 5 и равно геометрической сумме напряжений U +Uj -UXQ-О-уо . В общем случае на выходе сумматора 5 имеют напряжение, равное URi или U(Ч (фиг. 2) . С выхода сумматора 5 напряжение поступает через линейный выпрямитель 7 и фильтр 9 низших частот на вход блока 11 сравнения. На другой вход блока сравнения поступает опорное напряжение Од. Когда напряжения, подаваемые на входы блока 11 сравнения, оказываются равными (UB,UC) / напряжение на выходе амплитудного мо- дулятора 4 соответствует йу. При изменении величины входного сигнала в определенных пределам конец вектора напряжения Uj на выходе сумматора 5 будет описывать дугу окружности с радиусом, равным значению опорного напряжения U,. величина радиуса воспроизводимой окружности регулирует ся изменением величины напряжения Ug Величина й, соответствующая определенному значению напряжения U, пропорциональна ординате воспр9изводимой окружности. Напряжение U поступает на вход блока 6 масштабного преобразования. Напряжение на выходе 5лока 6 равно й -KnUv и пропорционально ординате моделируемого эллипса.
Таким образом, предлагаекый функциональный преобразователь позволяет осуществлять точное (без методической погрешности) моделирование центральных кривых второго порядка (эллипсы, окружности) с осями, параллельными осям координат.
При приближенном моделировании
Q нелинейных зависимостей путем их аппроксимации дугами указанных центральных кривых параметры настройки ,функционального преобразователя (величина опорного напряжения Uc, коэф- фициент аффинного подобия Kg, значение напряжений So находятся в,результате решения задачи аппроксимации , в которой аппроксимирующим выражением является уравнение эллипса. Это уравнение можно записать
0 в следующем виде, удобном для решения задачи аппроксимации:
; N-- % U. ,-и,„)25.Си4-и|)Г Ч )
Уравнение (4) получено из канонического уравнения эллипса (1) с помощью преобразования координат ПРИ переходе от системы координат ХОУ, совпадающей с осями эллипса к системе координат ХОУ. С помощью
уравнения эллипса (4) и уравнения (если функция задана аналитически) или таблицы значений (если функция задана численно) аппроксимируемой функции составляется система уравнений по одному из известных математических методов, например по методу наименьших квадратов. Полученная система уравнений решается относительно неизвестных параметров эллипса: UQ и, , U,Q. По найденным
параметрам аппроксимирующего эллипса определяются параметры настройки Функционального преобразователя: U,,
KQ 40
Предложенный функциональный преобразователь позволяет без изменения схемы реализовать обратное функциональное преобразование. Этот вывод следует из уравнения (2), которое является обратимым:
f С5)
а
60 Полученное уравнение (5) дает алгоритм обратного функционального преобразования. Отличие от прямого преобразования состоит в изменении на постоянную величину Kg напряжения,
65 моделирующего ргщиус окружности по
отношению к прямому преобразованию (это сводится к изменению величины напряжения згоданного значения Vc.t и изменения коэффициента аффинного подобия на обратную величину 1/Kg(достигается изменением коэффициента передачи блока 6 масштабного преобразования) .
В случае моделирования эллипса с центром, не совпадающим с центром системы координат, в которой реализуется нелинейная зависимость, при обратном преобразовании изменяются также величины напряжений и что сводится к изменению коэффициента передачи су№ атора 5 по этим входам.
Таким образом, предложенный функциональный преобразователь обеспечивает решение более широкого круга задач, чем известный. Он не имеет рлетодической погрешности при воспроизведении центральных кривых второгс порядка, что позволяет повысить точность его работы по сравнению с известным.
Формула изобретения
Функционёшьный преобрэзователь, содержащий блок сравнения , источник синусоидального напряжения, сумматор, фазовращатель, включенный между выходом источника синусоидального .напряжения и первым входом сумматора, амплитудный модулятор, информационный вход которого соединен с выходом источника синусоидсшьного напряжения, а выход - со вторым входом
сумматора, отличающийся тем, что, с целью расширения класса решаемых задач и повышения точности работы, он содержит блок масштабного преобразования, два линейных выпрямителя, два фильтра нижних частот, дополнительные блок сравнения и амплитудный модулятор, информационный вход которого подключен к выходу фазовращателя, управлянндий вход - к выходу, основного блока сравнения, а выход - ко входу блока масштабного преобразования и к третьему входу сумматора, выход сумматора через последовательно соединенные первый линейный выпрямитель и первый фильтр нижних частот соединен с первым входсж основного блока сравнения, второ вход которого соединен с шиной опорного напряжения, выход основного амплитудного модулятора через последовательно соединенные второй линейный выпрямитель и второй фильтр нижних частот соединен с первым входом дополнительного блока сравнения, выход которого подключен к управляющему входу основного амплитудного модулятора, а второй вход является входом преобразователя, выход блока масштабного преобразования является выходом преобразователя, выход источника синусоидального напряжения соединен с четвертым входом сумматора.
Источники информации, принятые во внимание при экспертизе
Uc
Т
Авторы
Даты
1981-08-30—Публикация
1979-10-08—Подача