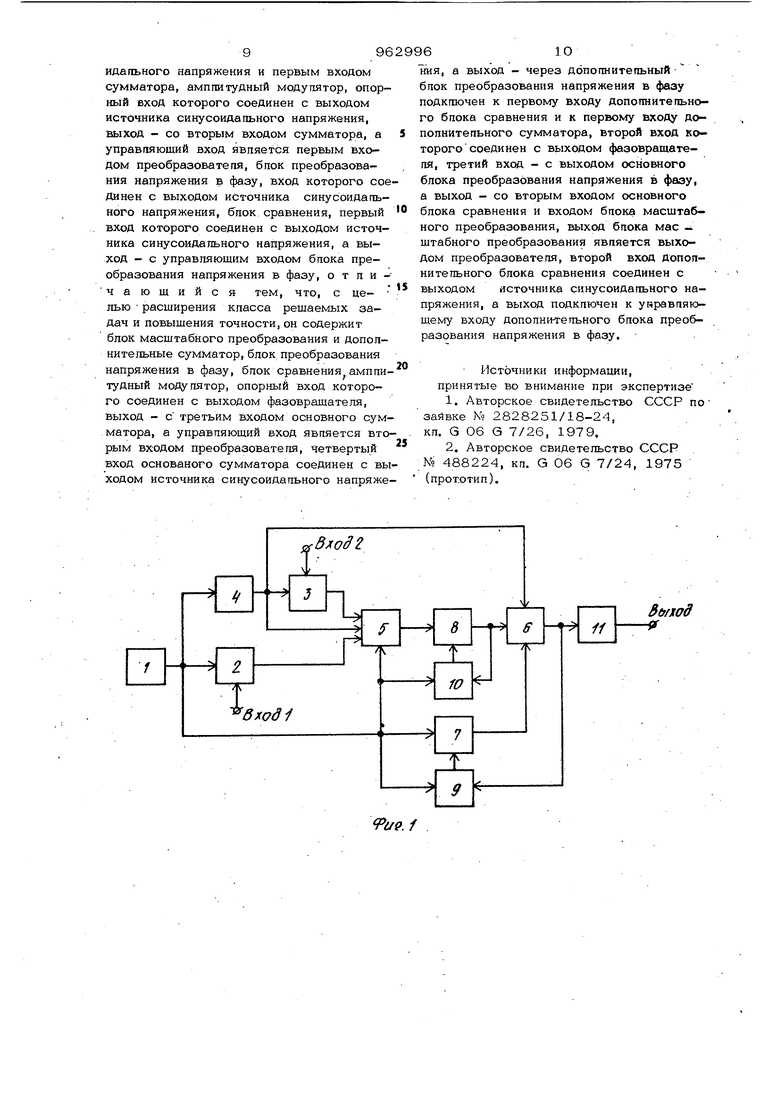
Изобретение относится к анапоговой вычиспитепьной технике. Известен функциональный преобразоватепь, содержащий генератор синусоидапьного напряжения, фазовращатегаь, амплитудный модулятор,, два блока сравнения, масштабный блок, сумматор, два линейных выпрямителя и два фильтра нижних частот, который воспроизводит центральные кривые второго порядка Cl J. Недостатком данного преобразователя является то, что он не позволяет моделировать эллипсоиды вращения. Наиболее близким к предлагаемому по технической сущности является функциональный преобразователь, содержащий источник синусоидального напряжения, сумматор, фазовращатель, включенный между выходом источника синусоидального на- пряжения и первым входом сумматора, амплитудный модулятор, опорный вход ко торого соединен с выходом источника синусоидального напряжения, выход - со вторым входом сумматора, а управгшющий вход является входом преобразователя, блок преобразования напряжения в фазу, включенный между выходсй источника синусоидального напряжения и третьим входом сумматора, выход которого является выходом преобразователя и подключен к первому входу блока сравнения, соединенного выходом с управляющим входом блока преобразования напряжения в фазу, а вторым входом - с выходом источника синусоидального напряженияСЗ Однако данный преобразователь является преобразователем функций одной переменной и не позволяет осуществлять точное (без методической ощибки) моделирование эллипсоидов вращения, а также реализовать аппроксимацию функций двух аргументов указанными поверхностями. Цель изобретения - расширение класса решаемых задач и повышение точности работы преобразователя. Указанная цель достигается тем, что функциональный преобразователь, содержа396ший источник синусоидального напряжения, сумматор, фазовращатель, включенны между выходом источника синусоидально го напряжения и первым входом сумматора, амплитудный модулятор, опорный вход которого соединен с выходом источника синусоидального напряжения, выход - со , вторым входом сумматора, а управляющий вход является первым входом преобразователя, блок преобразования напряжения в фазу, вход которого соединен с вы ходом источника синусоидального напряжения, блок сравнения, первый вход которого сое/;1инен с выходом источника синусоид а,шного напряжения, а выход - с управляющим входом блока преобразования напряжения в фазу, дополнительно содержит бпок масштабного преобразования и допо пни тельные сумматор, блок преобразо вания напряжения в фазу, блок сравнения, амплитудный модулятор, опорный вход которого соединен с выходом фазовращателя, выход - с третьим входом основного сумматора, а управляющий вход является вторым входом преобразователя, четвертый вход основного сумматора соединен с выходом источника синусоидального напряжения, а выход - через дополнительный блок преобразования .напряжения в фа зу подключен к первому входу дополнительного блока сравнения и к первому входу дополнительного сумматора, второй вход соединен с выходом фазовращателя, третий вход - с выходом основного блока преобразования напряжения в фазу, а выход - со вторым .входом основного блока сравнения и входом блока масштабного преобразования, выход блока масштабного преобразования является выходом преобразователя, второй вход дополнительного блока сравнения соединен с выходом источника синусоидального напряжения, а выход подключен к управляющему входу Дополнительного блока преобразования напряжения в фазу. На фиг. 1 приведена блок-схема функционального преобразователя; на фиг. 2диаграмма напряжений, поясняющая .-его работу. . Функциональный преобразователь содер жит источник 1 синусоидального напряжения, основной 2 и дополнительный 3 амппитудньш модуляторы, фазовр ащатель 4, основной 5 и дополнительный 6 сумматоры, основной 7 и дополнительный 8 блоки преобразования напряжения в ф)азу, основной 9 и дополнительный Ю блоки срав нения и блок 11 масштабного преобразования. Функциональный преобразователь работ следующим образом. Работа преобразователя основана на лизации алгоритма, полученного испольанием векторно-электрического метои применением афинного преобразовасферической поверхности. Этот а)горитм можно пояснить следуим образом. Уравнение эллипсоидов щения, смещенных относительно центсистемы координат, в которой осущестется моделирование, имеет вид го (и,-и, xo)(U4-4of , и ии,- напряжения, пропорциональные по-величине первой X и второй Y независимым переменным; напряжение, пропорциональное зависимой переменной 2 равное ординате точки эллипсоида в системе координат XYZ; напряжение, пропорциональное по величине полуоси эллипсоида вдоль осей / и X, напряжение, пропорциональ ное по величине полуоси эллипсоида вдоль оси 2., w LI мУ - напряжения, определяющие XOi 1о ZO смещение центра эллипсоида относительно центра системы координат XY2-; коэффициент аффинного подобия;напряжение, пропорциональное по величине ординате точки, лежащей на поверхности сферы с радиусом Uq в системе координатXY 2Как видно из уравнения (1), эллипсовращения может быть получен путем ейного р;астяжения или сжатия сферикой поверхности с радиусом, -равным уосям эллипсоида, вдоль оси зависипеременной 2- Степень линейной демации сферы определяется величиной ффициента аффинного подобия КдМоделирование сферических поверхносв предлагаемом преобразователе осутвляется следующим образом. Сначала производится векторное сумование напряжений согласно уравне XY-VW- Jxo- oгде и и UY - синусоидальные напряжения сдвинутые по фазе на tit/2 и пропорциональные по величине аргументам У и Y соответственно; и/ и и - синусоидальные напряжения . сдвинутые по фазе на ±Т/2. и определяющие смещение центра эллипсоида вдопь осей и Y. В результате суммирования в соответствии с ур/авнением (2) получено напря жение и смещенное по фазе относительно напряжений ОуИ Uy и определяющее положение проекции искомой точки, лежащей на поверхности эллипсоида, на ппоскость аргументов в системе координат УХ2; совпадающей с осями эллипсоида. Для того, чтобы определить величину напряжения, пропорционального ординате точки, лежащей на поверхности сферы, необходимо смоделировать сечение сферы проходящее через ее вертикальную ось и вектор напряжения UR (фиг. 2). Таким сечением, независимо от фазы напряжения ОГ7, всегда будет окружность с радиусом, равным радиусу сферы. При этом угол между осью X и вектором напряжения всегда равный 1С/2. Поэтому для. того, чтобы моделировать окружность в плоскости сечения, необходимо .предвари тельно изменить фазу напряжения Осу так КИМ образом, чтобы она совпадала с фаЗОЙ одного из напряжений Uy или Uy, сдви нутых на 11/2.. В этом случае другое напря жение можно использовать для моделирования ординаты UT. учетом сказанного уравнение окружности в ппоскости сечения можно записать в виде (3) синусоидальное напряжение, определяющее смещение центра сферы вдоль оси Z, сдвинутое по фазе относительно напряжения Оу на t-TC/l; Un - синусоидальное напряжение, постоянное по величине и регулируемое по фазе;. iL- - синусоидальное напряжение, раь ное по величине напряжению Uy Y совмещенное по фазе с напряжением UvПри суммировании напряжений согласно уравнению (3) и выполнении условия (Uz/OscY), (4) еличина напряжения О равна ординате окружности в ппоскости сечения и ординате сферы в системе координат М2-Дпя получения напряжения равного по величине ординате соответствующего эпгшп са в плоскости сечения и ординате эппип- соида в системе XYZ, необходимо произвести линейное масштабирование напря жения и 7. в соответствии с ве mi чиной коэффициента аффинного подобия Кд .. Воспроизведение функций осуществпяется следующим образом, Напряжение 1)7 выхода истоЧника 1 синусоидального напряжения поступает на входы амплитудного модулятора 2, фазо- вращатепя 4, сумматора 5, блоков 9 и 10 сравнения и блока 7 преобразования напряжения в фазу. Напряжение с выхода фазовращателя 4, сдвинутое по фазе на -JC/i относительно напряжения и.,поступает на опорный вход модулятора 3. На управляющий вход модулятора 2 поступает сигнал постоянного тока, пропорциональный по величине первому аргументу, а на управляющий вход модулятора 3 - пропорциональный второму аргументу, Напряжение U с выхода модулятора 2 пропорциональное по величине аргументу у, и совпадающее по фазе с напряжением источника 1 синусоидального напряжения, поступает на второй вход сумматора 5, на третий вход этого сумматора поступает напряжение Uy с выхода модулятора 3, пропорционапьное по величине второму аргументу V ч сдвинутое по фазе относительно напряжения Uy, на 7i|2. ,На четвертый вход сумматора 5 поступает на- пряжение с выхода фазовращателя 4. При этом коэффициент передачи сумматора 5 по первому входу устанавливается U o/Uf-, по второму и третьему - 1, а по четвер - тому - Uy /-г выходе сумматора 5 устанавливается в соответствии с уравнекием (2) напряжение , которое подается на вход блока 8- преобразования напряжения в фазу. На его выходе в обшем случае имеем напряжение ,равное по величине напряжению произволь. ное в общем случае по фазе. Напряжение подается на второй вход блока 10 сравнения. Если разница фаз между не„ряжением и напряжением Ur равна нулю, то сигнал на. выходе блока 10 сравнения также равен нулю. В случае отклонения разницы фаз напряжений и 0)- от нупя на выходе блока 10 сравнения появляется сигнал рассогласования который поступает на управляющий вход блока 8 преобразования напряжения в фа зу. В результате регулирования происходит совмещение фазы напряжения с фазой напряжения источника 1. Далее напряжениеи;; подается на первый вход сумматора 6, на второй вход- которого поступает напряжение с выхода фазовращателя 4, а на третий - напряжение с выхода блока 7 преобразования напря жения в фазу. Коэффициент передачи сумматора 6 по второму входу равен а по другим входам равен 1. На выходе сумматора 6 формируется напряжение Oz в соответствии с уравнением (3), имеющее в общем случае произвольную величи ну и фазу. Это напряжение поступает на второй вход блока 9 сравнения. При раз нице фаз между напряжениями Оу и Ur равной ft/-2, сигнал на выходе блока 9 сравнения равен нулю. При отклонении этой разницы фаз от ft/a на выходе блока 9 сравнения появляется сигнал, который поступает на управляющий вход блока 7 преобразования напряжения в фазу. В резул ьтате регулирования фаза напряжения U-2, устанавливается 7t/2,т.е. вы полняется условие (4). Следовательно, величина напряжения О2. равна ордина те некоторой точки сферической поверхности, соответствующей величине независ мых переменных 0 и О-у. Напряжение U посч пает на вход масщтабного блока 11 имеющего коэффициент передачи Кд.На выходе 11 установится в соотВет ствии с выражением (5) напряжение равное по величине ординате соответствующей точки, лежащей на поверхности эллипсоиду с параметрами Ц(о Таким образом, предлагаемый преобразоватегЖ позволяет осуществлять точное (без методической погрешности) моделирование сферических поверхностей и эллипсоидов вращения, уравнения которых являются функциями двух аргументов и встречаются при решении многих задач. . Кроме того, преобразователь может найти широкое применение при моделирова- НИИ траекторий движения различных объектов в трехмерном пространстве, когда движение объектов производится по указанным поверхностям. Предлагаемый, преобразователь позволяет также осуществлять приближенное воспроизведение щирокого класса функций двух независимых переменных путем аппроксимации указанными поверхностями второго порядка. Параметры настройки функционального преобразователя в этом случае находятся при решении задачи аппроксимации, в которой аппроксимирующим выражением является уравнение эллипсоида (1). В результате решения этой задачи определяются параметры аппроксимирующего эллипсоида:Хо,Ур и Кд. Если точность получаемая при аппроксимации одним эллипсоидом, недостаточна, то используется кусочно-нелинейная аппроксимация, при этом весь диапазон изменёния функции разбивается на несколько участков аппроксимации, для каждого из которых .производится расчет своих параметров аппроксимации. Указанный вид аппроксимирующей функции будет особенно удобен при аппроксимации выпуклых или вогнутых функций двух переменных, имеющих большое значение при решении различных оптимизационных задач. Следует отметить, что аппроксимирующее .выражение (1) предлагаемого преобразователя является.более сложным, чем у известных, что позволяет уменьшить погрешность аппроксимации. Кроме того, предлагаемый преобразователь позволяет без изменения схемы, реализовать обратное функциональное преобразование по каждому из аргументов. Этот вывод следует из уравнения (1), которое является обратимым для каждого аргумента (), VuS-LCV x-Uo},CUx-Uxof 3. Как видно из полученных уравнений, отличие обратного функционального преобраования от прямого по каждому из вхо ов состоит в изменении величины коэфициента аффинного подобия. Таким образом, предлагаемый преобазователь обеспечивает решение более ирокого круга задач, чем известный. н позволяет воспроизводить без метоической ошибки центральные поверхноси второго порядка и осуществлять ими ппроксимацию . широкого класса функций вух переменных. Формула изобретения Функциональный преобразователь соержащий источник синусоидального наряжения, сумматор, фазовращатель, вклюенный между выходом источника синусо99629идапьного напряжения и первым входом сумматора, амплитудный модулятор, опорный вход которого соединен с выходом источника синусоидапьного напряжения, выход - со вторым входом сумматора, а управпяюший вход является первым входом преобразоватепя, блок преобразоваНИН напряжения в фазу, вход которого соеДинен с выходом источника синусоидального напряжения, блок сравнения, первый вход которого соединен с выходом источвика синусоидального напряжения, а выход - с управляющим входом блока преобразования напряжения в фазу, о т л и чающийся тем, что, с це- лью расширения класса решаемых задач и повышения точности, он содержит блок масштабного преобразования и дополнительные сумматор, блок преобразования напряжения в фазу, блок сравнения амплитудный модулятор, опорный вход которого соединен с выходом фазовращателя, выход - с третьим входом основного сумматора, а управляющий вход является вторым входом преобразователя, четвертый вход основаного сумматора соединен с выходом источника синусоидального напряже5610 Икя, а выход - через дбпопнитепьный блок преобразования напряжения в фазу подключен к первому входу допопнитепьного блока сравнения и к первому входу дополнитепьного сумматора, второй вход которого соединен с выходом фазовращателя, третий вход - с выходом основного блока преобразования напряжения в фазу, а выход - со вторым входом основного блока сравнения и входом блока масштабного преобразования, выход блока мае - штабного преобразования является выхоДом преобразователя, второй вход дополнитепьного блока сравнения соединен с выходом источника синусоидального напряжения, а выход подключен к унравляюшему входу допопнит-ельного блока преобразования напряжения в фазу. Источники информации, принятые во внимание при экспертизе 1.Авторское свидетельство СССР по заявке Кз 2828251/18-24, кл. G 06 6 7/26, 1979. 2,Авторское свидетельство СССР № 488224, кл. G 06 G 7/24, 1975 (прототип).



| название | год | авторы | номер документа |
|---|---|---|---|
| Функциональный преобразователь двух переменных | 1983 |
|
SU1109766A1 |
| Функциональный преобразователь | 1980 |
|
SU934502A1 |
| Функциональный преобразователь | 1981 |
|
SU955113A1 |
| Функциональный преобразователь | 1979 |
|
SU860089A1 |
| Аппроксимирующий функциональный преобразователь | 1983 |
|
SU1104542A1 |
| Функциональный преобразователь | 1983 |
|
SU1137488A1 |
| Устройство для формирования ординат эллипса | 1980 |
|
SU1003107A1 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ПРЯМОУГОЛЬНЫХ КООРДИНАТ В ПОЛЯРНЫЕ | 1992 |
|
RU2085995C1 |
| Логарифмический преобразователь | 1979 |
|
SU790003A1 |
| Устройство для формирования функции эллипса | 1983 |
|
SU1133600A1 |



Авторы
Даты
1982-09-30—Публикация
1981-02-25—Подача