(Б ) ФУНКЦИОНАЛЬНЫЙ ПРЕОБРАЗОВАТЕЛЬ


| название | год | авторы | номер документа |
|---|---|---|---|
| Функциональный преобразователь | 1980 |
|
SU879603A1 |
| Устройство для вычисления коэффициентов разложения функции в ряд | 1981 |
|
SU962974A1 |
| Функциональный преобразователь | 1978 |
|
SU748443A1 |
| Функциональный преобразователь | 1979 |
|
SU911553A1 |
| Коррелометр | 1988 |
|
SU1674165A1 |
| Многоканальный автокоррелятор | 1989 |
|
SU1718242A1 |
| Устройство для вычисления коэффициентов разложения функций в ряд | 1981 |
|
SU1029189A1 |
| Кусочно-квадратичный аппроксиматор | 1982 |
|
SU1091187A1 |
| Устройство для вычисления коэффициентов разложения функции в ряд | 1980 |
|
SU881761A1 |
| Время-импульсный анализаторСигНАлА | 1979 |
|
SU817725A1 |


1
Изобретение относится к автоматике и вычислительной технике и может найти применение, в частности, в устройствах, предназначенных для кусочно-квадратичной аппроксимации произвольных функций, и является усовершенствованием известного функционального преобразователя.
По основному авт. св. № 879603 известен функциональный преобразователь, содержащий две группы ключей, инвертор, регистр сдвига, группу из VI интеграторов (где п+1 - количество членов ряда аппроксимирующих функций) и группу основных аналоговых блоков взвешенного суммирования, каждый из которых подключен входами к выходам интеграторов, причем каждый i-й (liS ) ключ первой группы ключей соединен сигнальным входом с шиной ввода выборочных значений входного сигнала и с входом инвертора, а выходом - с входом
i-ro интегратора, каждый i-й ключ второй группы ключей подключен сигнальным входом к выходу инвертора., а выходом - к входу (-f1)-ro интегратора, а регистр сдвига соединен входом с шиной ввсэда тактовых импульсов, а выходом каждого -го разряда - с управляющими входами 1-х ключей первой и второй групп ключей Ci .
Недостатком известного устройства является пониженная точность функционального преобразования из-за кусочно-линейного характера аппроксимации функции.
Цель изобретения - повышение томности функционального преобразования. .
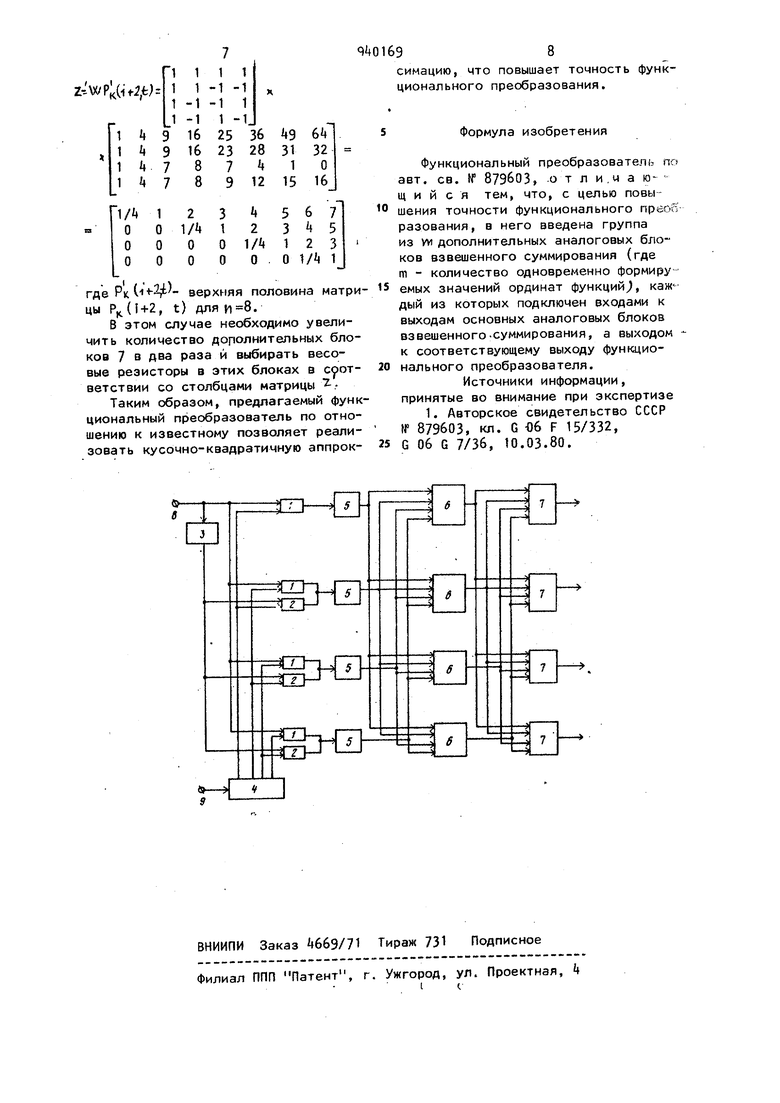
Указанная цель достигается тем что в функциональный преобразователь введена группа из m дополни- . тельных аналоговых блоков взвешенного суммирования (где m - количество одновременно формируемых значений ор39 0169динат функции), каждый из которых подключен входами к выходам основных аналоговых блоков взвешенного суммирования, а выходом - к соответствующему выходу функционального . преобразователя. На чертеже изображена блок-схема функционального преобразователя для случая n-m-. Преобразователь содержит первую и вторую группы 1 и 2 ключей, инвертЬр 3, регистр k сдвига, группу из п интеграторов 5 (где пч-1 - количество членов кода аппроксимирующий функций) , группу основных аналоговых блоков 6 взвешенного суммирования и группу из m дополнительных аналоговых блоков 7 взвешенного суммирования (где m - количество одновременно формируемых значений ординат функции), Каждый из дополнительных блоков 7 подключен входами к выходам основных блоков 6 взвешенного суммирования, а выходом - к соответствующему выходу функционального преобразователя. Каждый из основных блоков 6 подключен входами к выходам интеграторов 5« Каждый i-и (1 i €п) ключ 1 первой группы ключей соединен сиi- нальным входом с шиной 8 ввoдf выборочных значений входного сигнала и с входом инвертора 3, а выходом .с входом 1-го интегратора 5. Каждый I-и ключ 2 второй группы ключей подключен сигнальным входом к выходу инвертора 3, а выходом - к входу (i-f f1)-ro интегратбра 5. Регистр k сдвига соединен входом с шиной Э ввода тактовых импульсов, а выходом каждого 1-го разряда - с управляющими входами i-x ключей 1 и 2 первой и второй групп ключей. Аналоговые блоки 6 и 7 взвешенного суммирования могут быть реализованы, например, на операционных усилителях с весовыми резисторами на вхрдах. Предлагаемый функциональный преобразователь реализует кусочно-квадратичное представление входного сигнала вместо кусочно-линейного, используемого в известном. Разложение сигнала f(t) с помощью кусочно-линейных базисных функций Уолша можно представить в виде f (t) .pci,t;, (1) где P(i,t) - интегральные функции Уолша, которые определяются, как гд W 5 . фу «о ин 5 гд ку ци дл Рк Ма из гд цы Citi,i)-IwAHi)(,| (2) ,1,2,...; P(0, t)1; W.t)- функции Уолша; Т интервал задания аргумента t. усочно-квадратичные базисные ции Р (i+2, t) получаются путем грирования P(i+l, t) + 2,4.)--cJpti4i,i)dr, (3) о С - постоянная нормирования P(0,t)--f; p,t)p(i,t) азложение сигнала с помощью чно-квадратичных базисных функPJ C-H , t) можно представить Si)--.,PKti,t). атрица преобразования Р,(1+2, t) I «8 имеет вид 4 9 16 25 36 ЦЭ 6 16 23 28 31 32 О 8 9 12 15 72в 0121 О -1 -2 -1 321 1 5 6 J ицу (5 можно представить как продение двух матриц , (6) V/ - матрица преобразования Уолша. ) лементы верхне-треугольной матриопределяются следующим образом;
ci
o(a.
ЯZ
Обратная матрица Z будет иметь
вид Z представляет собой нмжне-треугольную матрицу, элементы главной диагонали которой равны единице, пе вой поддиагонали -3, второй 1, третьей -, четвертой 4 и т.д. В матричной форме уравнение () пишется в виде 5-сХ/ вектор-строка аппроксимиру емой функции , вектор-строка коэффициенто разложения по кусочно-квад ратичным базисным функциям Р . -t-p -R - К В то же время из ( б) Р;-- Тогда, подставляя ((} и (Ю) в С8) с учетом транспортирования ( 6), (получаем -ч ;j- . X - вектор-столбец заданной дискретной последовательности f(t). Таким образом, для получения аппроксимированного значения функции в любой момент времениt необходимо ВЫЧИСЛИТЬ коэффициенты разложения по преобразованию ги умножить полученные коэффициенты на матрицу Z . В то же время 1 можно представит как произведение двух матриц чг. (V2)
-1
представляет собой матрицу,
деГ элементы которой на главной диагонали равны 1 и на первой поддиагонали равны -1;
-f
to
15
-г 1
,--lV,Za, X. Преобразователь работает следуго1цим образом. ину 8 с тактовой частотой поступает процесс X(t), который в зависимости от вида матрицы 1 поступает непосредственно на сигнальные входы ключей 1 или в инвертированном виде на сигнальные входы ключей 2. Работой ключей t и 2 управляет регистр сдвига, выходы разрядов которого в зависимости от вида матрицы 2 подключены к управляющим входам соответствующих ключей 1 и 2. После прихода с шины 9 на вход регистра Ц п импульсов на выходах интеграторов 5 формируются коэффициенты преобразования по i Которые в блоках 6 суммируются в соответствии с весовыми значениями строк матрицы 2 (нулевым весам в матрице соответствуют бесконечно большие значения весовых резисторов, т.е. отключение соответствующих входов блоков 6), в результате чего на выходах основных блоков 6 взвешенного суммирования будут присутствовать напряжения, пропорциональные коэффициентам раз ложения . Эти напряжения поступают на входы дополнительных блоков 7 взвешенного суммирования, с помощью которых реализуется перемножение коэффициентов столбцы матрицы Z и суммирование.. i Для получения промежуточных зна,чений fno отношению к входным отсчеTaM) аппроксимируемой функции необходи МО умн |«ить вектор-строку коэффициентов Сх на Z , Для 1111 1 1-1-1 Z--V(/PK( 1-1-1 1 1-1 1-1 1i Э162536 96 4 1i 91623283132 1it787 1 0 1 4789121516 1Л123 567 001Л1 00001Л1 2 3 0000 0 .0 l/i 1 где PK ( верхняя половина мат цы , t) для . В этом случае необходимо увели чить количество дополнительных бло ков 7 в два раза и выбирать весовые резисторы в этих блоках в соо ветствии со столбцами матрицы 2.Таким образом, предлагаемый фу циональный преобразователь по отн шению к известному позволяет реали зовать кусочно-квадратичную аппро s симацию, что повышает точность функционального преобразования. Формула изобретения Функциональный преобразователь по авт. св. If 879603, от л и,ч а ю щ и и с я тем, что, с целью повышения точности функционального преой разования, в него введена группа из wi дополнительных аналоговых блоков взвешенного суммирования (где m - количество одновременно формируемых значений ординат функций, каж дый из которых подключен входами к выходам основных аналоговых блоков взвешенного.суммирования, а выходом к соответствующему выходу функционального преобразователя. Источники информации, принятые во внимание при экспертизе 1. Авторское свидетельство СССР № 879603, кл. G 06 F 15/332, G Об G 7/36, 10.03.80.
Авторы
Даты
1982-06-30—Публикация
1980-04-30—Подача