Изобретение относится к области радиолокации, а именно к оценке углового положения источника электромагнитного излучения в пространстве. Устройство может быть использовано для измерения углов и угловых рассогласований на источник электромагнитного излучения в пространстве, для измерения траекторий движения объектов в составе радиолокационных и радионавигационных систем, устройств.
Известен фазовый пеленгатор системы Мини Трек, предназначенный для определения траекторий движения искусственных спутников Земли. Устройство содержит 8 антенн точного определения угловых координат источника излучения и 5 антенн для устранения неоднозначности.
Недостатками такого пеленгатора является то, что в нем используется последовательный способ устранения неоднозначности отдельно по каждому из ортогональных рядов антенн, что приводит к увеличению результирующей вероятности аномальной ошибки.
Наиболее близким по техническому решению является фазовый пеленгатор, содержащий 5 слабонаправленных антенных элементов, располагающихся на двух перпендикулярных плечах, образуя крестообразную антенную структуру, причем один из элементов расположен в точке пересечения плеч, 5 приемно-усилительных трактов и 4 фазометра, два из которых подключены к антеннам одного плеча, а два других - между антеннами другого плеча, кроме того, выходы первых двух фазометров подключены к двум входам первого устройства устранения неоднозначности, а выходы других двух фазометров - к двум входам второго устройства, устранения неоднозначности. Выходы устройств устранения неоднозначности подключены к двум входам вычислителя координат углового положения источника излучения.
Недостатками такого фазового пеленгатора является то, что в нем применяется последовательный способ устранения неоднозначности отдельно по каждому из ортогональных рядов антенн, что приводит к увеличению результирующей вероятности аномальной ошибки.
В устройство пеленгования, содержащее N расположенных на плоскостях антенных элементов, образующих m измерительных баз, N приемников, подключенных к выходам N антенных элементов, m фазометров, входами подключенных к выходам приемников m измерительных баз, введено (m-2) первых весовых сумматоров, (m-2) блоков округления до целого, m вторых весовых сумматоров, два третьих весовых сумматора и два блока выделения остатков от округления до целого, m входов (m-2) первых весовых сумматоров соответственно объединены и подключены к выходам m фазометров соответственно, выходы которых подключены соответственно к входам (m-2) блоков округления до целого, первые m входов двух третьих весовых сумматоров соответственно объединены и подключены к выходам m фазометров соответственно, (m-2) входов m вторых весовых сумматоров соответственно объединены и подключены к выходам (m-2) блоков округления до целого соответственно, вторые m входов двух третьих весовых сумматоров соответственно объединены и подключены к выходам m вторых весовых сумматоров, выходы двух третьих весовых сумматоров подключены соответственно к входам двух блоков выделения остатков от округления до целого, выходы которых являются выходами устройства по двум переменным направления, причем антенные элементы размещены произвольно на плоскости.
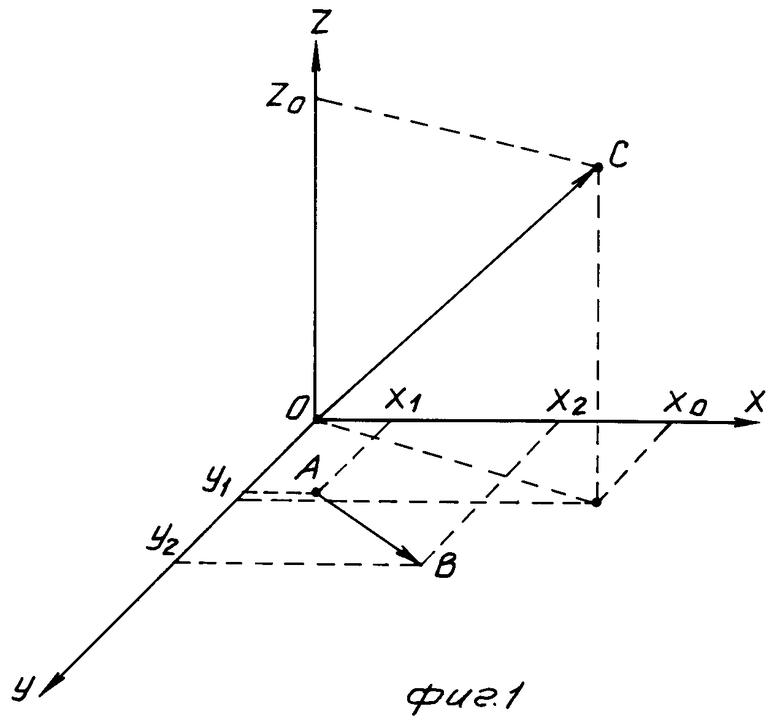
Полная разность фаз ΔΦ между антеннами, расположенными в точках A(x1, y1) и B(x2, y2) равна 2 πd/λ , где d - проекция вектора AB на вектор OC, где 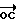 (cos α, cos β, cos γ) - единичный вектор нормали к плоскому фронту волны, следовательно
(cos α, cos β, cos γ) - единичный вектор нормали к плоскому фронту волны, следовательно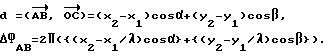 .
.
Для n-базовой системы с учетом, что разность фаз практически содержит флуктуационную составляющую ζ, вводя обозначения: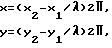 получим
получим +
+ =
=  cosα+
cosα+ cosβ+
cosβ+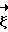 , где
, где  - вектор дробных значений разностей фаз;
- вектор дробных значений разностей фаз; - вектор целых значений разностей фаз;
- вектор целых значений разностей фаз;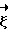 - вектор флуктуационных составляющих. Логарифм функции правдоподобия направляющих косинусов при условии, что фазовые ошибки распределены нормально, имеют нулевое среднее и известную корреляционную матрицу, с точностью до постоянного множителя может быть записан следующим образом:
- вектор флуктуационных составляющих. Логарифм функции правдоподобия направляющих косинусов при условии, что фазовые ошибки распределены нормально, имеют нулевое среднее и известную корреляционную матрицу, с точностью до постоянного множителя может быть записан следующим образом:
П (cosα, cosβ)= (
(cosα, cosβ)= ( +
+ -
- cosα-
cosα- cosβ)тB-1(
cosβ)тB-1( +
+ -
- cosα-
cosα- cosβ),
cosβ),
где В-1 - симметричная матрица, обратная матрице В;
σ2 В - ковариационная матрица флуктуаций;
σ2 - их дисперсии. Без потери общности будем считать векторы  и
и  коллинеарными соответственно векторам
коллинеарными соответственно векторам  и
и  , координаты каждого из которых являются целыми взаимно простыми числами. Выполняются соответственно
, координаты каждого из которых являются целыми взаимно простыми числами. Выполняются соответственно = a
= a ,
,  = b
= b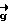 , где a, b - коэффициенты. Кроме того, от направляющих косинусов cos α, cosβ перейдем к переменным направления v и w, где
, где a, b - коэффициенты. Кроме того, от направляющих косинусов cos α, cosβ перейдем к переменным направления v и w, где
v = a cos α, w = b cos β. При этом логарифм функции правдоподобия переменных направления v и w:
П (v, w)= (
(v, w)= ( +
+ -v
-v -w
-w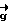 )тB-1(
)тB-1( +
+ -v
-v -w
-w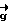 ) (1) Составляя уравнения правдоподобия при фиксированном векторе неоднозначности
) (1) Составляя уравнения правдоподобия при фиксированном векторе неоднозначности  и решая их, найдем оценки переменных направления
и решая их, найдем оценки переменных направления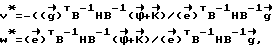 ), (2) , (2) где H=
), (2) , (2) где H=  (
(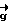 )т-
)т-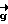 (
( )т - симметричная матрица, обладающая свойством Нт = -Н:
)т - симметричная матрица, обладающая свойством Нт = -Н: ,
, 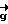 - должны быть линейно независимыми, иначе логарифм функции правдоподобия не имеет экстремума.
- должны быть линейно независимыми, иначе логарифм функции правдоподобия не имеет экстремума.
Подставляя формулу (2) в формулу (1), получим логарифм функции правдоподобия вектора неоднозначности:
П (
( )= (
)= ( +
+ )тG(
)тG( +
+ ), (3)
), (3)
G= B-1+(B-1HB-1HB-1)/( )тB-1HB
)тB-1HB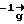 - симметричная матрица рагна (n-2).
- симметричная матрица рагна (n-2).
Оценка вектора неоднозначности 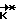 определяется из условия
определяется из условия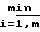 П
П (
(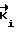 )= П
)= П (
(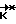 ) . (4)
) . (4)
Оценки переменных направления (2) вычисляются при  равном его оценке
равном его оценке 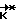 .
.
Геометрически линейная оболочка векторов  и
и 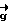 может быть названа плоскостью Q полных разностей фаз, так как в базисе из векторов
может быть названа плоскостью Q полных разностей фаз, так как в базисе из векторов  и
и 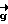 полная разность фаз v
полная разность фаз v +w
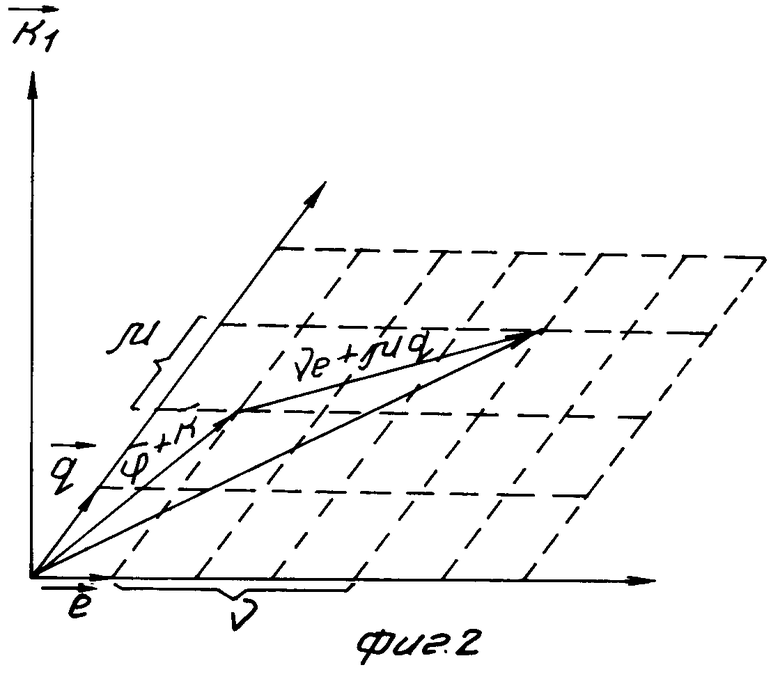
+w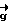 является радиусом вектором точек (v, w) ∈ Q (см. фиг. 2).
является радиусом вектором точек (v, w) ∈ Q (см. фиг. 2).
Оценку полной разности фаз можно рассматривать как составляющую суммы  +
+ в плоскости Q. Проектирование выполняется в соответствии с формулами (2).
в плоскости Q. Проектирование выполняется в соответствии с формулами (2).
Добавление к вектору  линейной комбинации
линейной комбинации 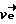 +
+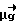 с любыми вещественными коэффициентами ν и μ приводит к увеличению оценок v* и w* на ν и μ соответственно.
с любыми вещественными коэффициентами ν и μ приводит к увеличению оценок v* и w* на ν и μ соответственно.
Следовательно, если оценка вектора неоднозначности определяется с точностью до слагаемого 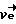 +
+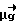 , где ν, μ - любые числа, то оценки переменных v* и w* неоднозначны и интервал однозначности 1. В этом случае оценки параметров направления нужно привести к интервалу однозначности, удаляя целую часть:
, где ν, μ - любые числа, то оценки переменных v* и w* неоднозначны и интервал однозначности 1. В этом случае оценки параметров направления нужно привести к интервалу однозначности, удаляя целую часть:
vo* = v* - Ent (v* + 0,5),
(5)
wo* = w* - Ent (w* + 0,5), где Ent(a) - операция выделения ближайшей целой части a. Алгоритм устранения неоднозначности (4) заключается в подборе такого целочисленного вектора неоднозначности  , который обеспечивает наименьшее расстояние конца вектора
, который обеспечивает наименьшее расстояние конца вектора  +
+ до плоскости Q. Это следует из того, что геометрически функция П
до плоскости Q. Это следует из того, что геометрически функция П (
( ) равна квадрату длины вектор-проекции суммы векторов
) равна квадрату длины вектор-проекции суммы векторов  и
и  на подпространство, дополняющее плоскость Q до пространства.
на подпространство, дополняющее плоскость Q до пространства.
В качестве векторов нового базиса можно взять линейно независимую систему векторов 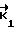 , . . . ,
, . . . , 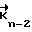 ,
,  ,
, 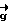 , где
, где 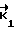 , . . . ,
, . . . , 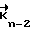 - векторы неоднозначности, имеющие наименьшую длину своих вектор-проекций на дополнительное подпространство среди всех других возможных векторов неоднозначности.
- векторы неоднозначности, имеющие наименьшую длину своих вектор-проекций на дополнительное подпространство среди всех других возможных векторов неоднозначности.
Обозначим вектор-проекции  и
и  на дополнительное подпространство через
на дополнительное подпространство через  и
и 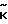 . Формулу (3) можно записать в виде
. Формулу (3) можно записать в виде
П (
(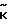 )= (
)= ( +
+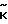 )
)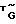 (
( +
+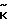 ), где
), где  = CтGC,
= CтGC,  = C-1ϕ,
= C-1ϕ, 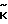 = C
= C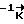 ,
,
C= (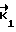 , . . . ,
, . . . , 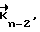
 ,
, 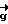 - матрица перехода от старого (нормального) базиса к новому, с-1 - обратная к ней. Алгоритм устранения неоднозначности в новом базисе
- матрица перехода от старого (нормального) базиса к новому, с-1 - обратная к ней. Алгоритм устранения неоднозначности в новом базисе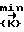 Пϕ(
Пϕ(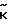 )= П
)= П (
(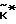 ), (6) Можно показать, что матрица
), (6) Можно показать, что матрица  имеет нулевые строки и столбцы с номерами (n-1) и n. Следовательно по алгоритму (6) формируются (n-2) первых координат оценки вектора неоднозначности
имеет нулевые строки и столбцы с номерами (n-1) и n. Следовательно по алгоритму (6) формируются (n-2) первых координат оценки вектора неоднозначности 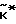 .
.
Чтобы найти вектор неоднозначности 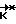 относительно старого базиса, соответствующий
относительно старого базиса, соответствующий 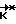 , нужно воспользоваться обратным переходом
, нужно воспользоваться обратным переходом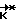 = C
= C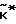 , (7) Но
, (7) Но 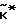 в этой формуле записи имеет n координат. В качестве двух последних координат полученного вектора
в этой формуле записи имеет n координат. В качестве двух последних координат полученного вектора 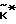 можно взять любые целые числа ν и μ.
можно взять любые целые числа ν и μ.
При этом по формуле (7) восстановим вектор неоднозначности с точностью до слагаемого 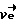 +
+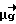 , так как
, так как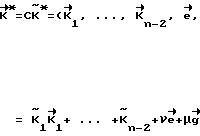
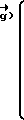
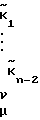
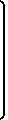 = . Однако это не влияет на оценки переменных направления ввиду отбрасывания в последующем целой части. Оценка вектора
= . Однако это не влияет на оценки переменных направления ввиду отбрасывания в последующем целой части. Оценка вектора 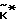 упрощается при условии, что верхняя угловая матрица матрицы равна единичной (или близка к ней), тогда
упрощается при условии, что верхняя угловая матрица матрицы равна единичной (или близка к ней), тогда
П (
(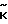 )= (
)= ( +
+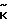 )тE(
)тE( +
+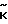 )= (
)= (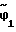 +
+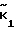 )2+ . . . +(ϕn-2+
)2+ . . . +(ϕn-2+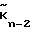 )2 П
)2 П (
(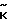 ) достигает min, когда каждая сумма в скобках минимальна. Наименьшее значение
) достигает min, когда каждая сумма в скобках минимальна. Наименьшее значение 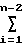 (ϕi+Ki)2 получим при векторе ki, равном ближайшему целому значению в ϕi.
(ϕi+Ki)2 получим при векторе ki, равном ближайшему целому значению в ϕi.
В качестве оценки 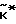 в этом случае можно взять вектор
в этом случае можно взять вектор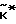 =
= 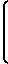
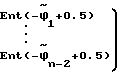 (8)
(8)
Изложенные принципы реализованы в предлагаемом устройстве пеленгования, что позволяет повысить достоверность оценок путем одновременного устранения неоднозначности фазовых измерений по двум углам пространства.
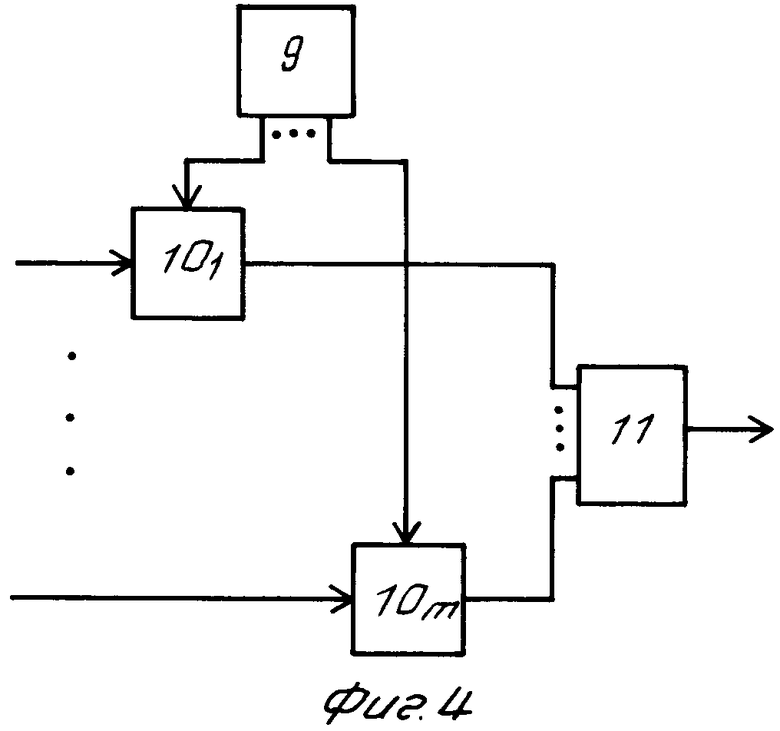
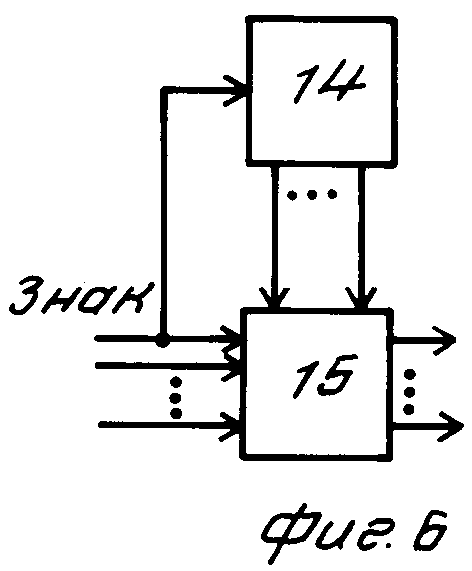
На фиг. 1 приведена геометрическая интерпретация принципа определения разности фаз; на фиг. 2 - геометрическая интерпретация к алгоритму работы устройства пеленгования; на фиг. 3 - функциональная схема устройства пеленгования; на фиг. 4 - функциональная схема m-входового весового сумматора; на фиг. 5 - функциональная схема блока округления до целого; на фиг. 6 - функциональная схема блока выделения остатков от округления.
Устройство пеленгования состоит из N антенных элементов 1, расположенных на плоскости, образующих m измерительных баз, N приемников 2, подключенных к выходам N антенных элементов, m фазометров 3, входами подключенных к выходам приемников m измерительных баз, например, одна из антенн является опорной и фазометры подключены между опорной и остальными антеннами, либо N/2 фазометров подключаются к N/2 отдельным парам антенн, (m-2) m-входовых первых весовых сумматоров 4, (m-2) блоков 5 округления до целого, m (m-2)-входовых вторых весовых сумматоров 6, два 2m-входовых третьих весовых сумматоров 7 и два блока 8 выделения остатков от округления до целого, m входов (m-2) первых весовых сумматоров 4 соответственно объединены и подключены к выходам m фазометров 3 соответственно, выходы которых подключены соответственно к входам (m-2) блоков 5 округления до целого, первые m входов двух третьих весовых сумматоров 7 соответственно объединены и подключены к выходам m фазометров 3 соответственно, (m-2) входов m вторых весовых сумматоров 6 соответственно объединены и подключены к выходам (m-2) блоков 5 округления до целого соответственно, вторые m входов двух третьих весовых сумматоров 7 соответственно объединены и подключены к выходам m вторых весовых сумматоров 6, выходы двух третьих весовых сумматоров 7 подключены соответственно к входам двух блоков 8 выделения остатков от округления до целого.
Устройство пеленгования работает следующим образом.
На антенные элементы 1, расположенные в плоскости, падает плоский фронт волны (так как источник излучения находится в дальней зоне AР). Сигналы, поступающие на вход приемоусилительных трактов 2, имеют различные фазы вследствие разноса антенных элементов плоской AР. В них сигналы усиливаются и подаются на фазометры 3, которые измеряют разность фаз между принимаемыми сигналами, но при этом теряется целое число периодов сигнала, так как область измерений фазометра лежит в пределах от - π до π и принимаемые сигналы являются гармоническими. Разности фаз (дробные их части, в единицах 2 π) с фазометров 3 поступают на весовые сумматоры 4, имеющие m входов, равное числу фазометров. На весовых сумматорах осуществляется взвешенное суммирование разностей фаз в соответствии с выражением: = C
= C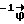 , с-1 - матрица, элементы которой заранее известны.
, с-1 - матрица, элементы которой заранее известны.
Новая совокупность разностей фаз {  } имеет размерность (m-2), так как число весовых сумматоров 4 равна (m-2). Совокупность разностей фаз {
} имеет размерность (m-2), так как число весовых сумматоров 4 равна (m-2). Совокупность разностей фаз {  } поступает на блок 5 округления до целого, где выделяется целая часть новой совокупности разностей фаз в соответствии с выражением (8) для получения оценки вектора неоднозначности.
} поступает на блок 5 округления до целого, где выделяется целая часть новой совокупности разностей фаз в соответствии с выражением (8) для получения оценки вектора неоднозначности.
Таким образом, осуществляется устранение неоднозначности по обоим углам пространства. Оценка вектора неоднозначности в новом базисе поступает на весовые сумматоры 6, где осуществляется переход к старому базису в соответствии с выражением (7). Вектор неоднозначности или вектор целых частей разностей фаз, а также вектор дробных частей разностей фаз поступают на весовые сумматоры 7, где получаются оценки параметров направления путем простого взвешенного суммирования в соответствии с выражением (2). Полученные оценки необходимо привести к интервалу однозначности. Этот процесс осуществляется в блоках 8 выделения остатков от округления в соответствии с выражением (5). Причем выходы блоков 8 выделения остатков от округления являются выходами устройства пеленгования.
На фиг. 4 изображен m-входовый весовой сумматор, который включает в себя m умножителей 10, запоминающее устройство 9, m-входовый сумматор 11. При работе весового сумматора на входы умножителей 10 поступают коды чисел, предназначенных для взвешенного суммирования. Здесь они умножаются на соответствующие коэффициенты, которые считываются с запоминающего устройства 9. Затем все эти m значений складываются друг с другом на сумматоре 11. Выход сумматора является выходом m-входового весового сумматора.
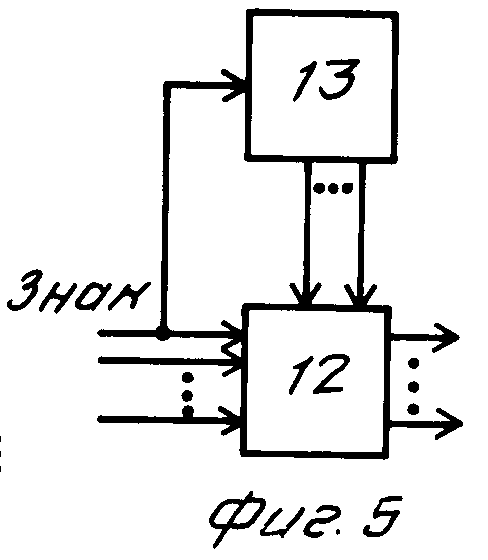
На фиг. 5 изображен блок округления до целого. Блок округления до целого состоит из сумматора 12 и запоминающего устройства 13. Блок округления до целого работает следующим образом: на вход сумматора 12 поступают целые и дробные разряды числа, подлежащего округлению, где они складываются с числом + 0,5, которые записаны в запоминающем устройстве 13. Знак числа 0,5 определяется знаком числа, подлежащего округлению. Если округляется положительное число, то прибавляется +0,5, если отрицательное, то -0,5. Таким образом, знаковый разряд поступает помимо сумматора еще и на запоминающее устройство. Выходами блока округления до целого являются выходы сумматора, соответствующие целым разрядам.
На фиг. 6 изображен блок выделения остатков от округления. Блок выделения остатков от округления состоит из сумматора 15 и запоминающего устройства 14. Работа этого блока аналогична работе блока округления до целого. Отличие в том, что выходами являются выходы сумматора, соответствующие дробным разрядам.
Устройство легко реализуется на элементах цифровой логики. Сумматоры 11, 12, 15 могут быть реализованы на микросхемах К 155ИМ3, умножители 10 выполняются на микросхемах КР 1802 ВР2. Запоминающие устройства 9, 13, 14 реализуются на микросхемах К 555 РЕ4.
В предлагаемом устройстве не существует ограничений на расположение элементов AP в плоскости. Кроме того, определение оценок параметров направления и устранения неоднозначности, которое осуществляется одновременно по двум углам пространства, реализовано на основе простейших математических операций в соответствии с максимально правдоподобным методом, что позволяет повысить достоверность устройства пеленгования.
Рассмотрим конкретный пример работы устройства пеленгования.
Пусть ошибки фазовых измерений допускаются в измерителях и тогда корреляционная матрица фазовых ошибок будет иметь вид

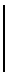




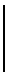 Пусть векторы масштабных коэффициентов по осям OX и OY будут иметь вид
Пусть векторы масштабных коэффициентов по осям OX и OY будут иметь вид 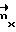 ≡
≡ 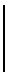
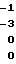
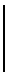
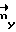 ≡
≡ 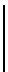
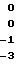
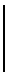 Достоверность оценок параметров направления характеризует вероятность правильного устранения неоднозначности. Для прототипа эта величина характеризуется произведением вероятностей по каждому из плеч. Вероятность правильного устранения неоднозначности по одному плечу равна:
Достоверность оценок параметров направления характеризует вероятность правильного устранения неоднозначности. Для прототипа эта величина характеризуется произведением вероятностей по каждому из плеч. Вероятность правильного устранения неоднозначности по одному плечу равна:
Po1 = P{ 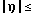 Π/
Π/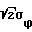 L } где η - случайная величина, распределенная нормально и с нулевым средним значением.
L } где η - случайная величина, распределенная нормально и с нулевым средним значением.
Для каждого случая пусть σϕ= π/6 и тогда получим при L = 3:
Po1 = 2 Φ* (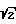 ) = 2˙0,4207 = 0,8414. Тогда
) = 2˙0,4207 = 0,8414. Тогда
Po = Po1˙ Po2 = P2o1 = 0,708. Подсчитаем теперь вероятность правильного устранения неоднозначности для устройства пеленгования.
Для векторов 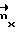 и
и 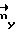 , описанных выше, матрица G имеет вид
, описанных выше, матрица G имеет вид
1/σ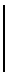
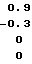
 -
-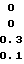
 Из общей совокупности возможных векторов неоднозначности подберем два вектора (так как ранг матрицы G равен (m-2), и при n = 4 интеграл вероятности правильного устранения неоднозначности будет двукратным) с наименьшими кодовыми расстояниями и линейно независимые, это
Из общей совокупности возможных векторов неоднозначности подберем два вектора (так как ранг матрицы G равен (m-2), и при n = 4 интеграл вероятности правильного устранения неоднозначности будет двукратным) с наименьшими кодовыми расстояниями и линейно независимые, это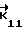 = (0100)т
= (0100)т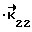 = (0001)т, кодовые расстояния dko и того и другого равны 0,1.
= (0001)т, кодовые расстояния dko и того и другого равны 0,1.
Корреляционная матрица случайных величин η будет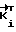 G
G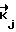 = Bij. Дисперсии вдоль координатной оси будут равны
= Bij. Дисперсии вдоль координатной оси будут равны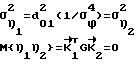 = d
= d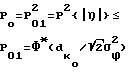 1/2×d
1/2×d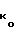 /
/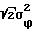 } при σϕ = 0,083 (что соответствует π/6)
} при σϕ = 0,083 (что соответствует π/6)
Pо= [Φ*(0.1/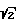 (0.083)2)] 2= [Φ*(10)] 3= 1. Ранее для прототипа было получено 0,708. (56) Бартоломе. Системы передачи информации и измерения параметров траектории искусственных спутников Земли и космических аппаратов. Зарубежная радиоэлектроника, 1966, N 2.
(0.083)2)] 2= [Φ*(10)] 3= 1. Ранее для прототипа было получено 0,708. (56) Бартоломе. Системы передачи информации и измерения параметров траектории искусственных спутников Земли и космических аппаратов. Зарубежная радиоэлектроника, 1966, N 2.
Ernest Jacobs, Elizabeth W. Ralstoon Amriquity Resolution in Interferometry, IEEE Trans. on Aerospace and electronic systems, vol. AES-17, N 6, 1981.
| название | год | авторы | номер документа |
|---|---|---|---|
| ФАЗОВЫЙ ПЕЛЕНГАТОР | 1989 |
|
RU2069866C1 |
| ФАЗОВЫЙ ПЕЛЕНГАТОР-ЧАСТОТОМЕР | 1993 |
|
RU2124216C1 |
| ФАЗОВЫЙ ПЕЛЕНГАТОР СКАНИРУЮЩИХ ИСТОЧНИКОВ | 1993 |
|
RU2073878C1 |
| МОНОИМПУЛЬСНЫЙ ПЕЛЕНГАТОР | 1993 |
|
RU2115134C1 |
| ПЕЛЕНГАТОР | 1993 |
|
RU2115133C1 |
| ДВУХКАНАЛЬНЫЙ ПЕЛЕНГАТОР | 1993 |
|
RU2078348C1 |
| ПЕЛЕНГАТОР СКАНИРУЮЩИХ ИСТОЧНИКОВ | 1992 |
|
RU2074404C1 |
| РАДИОПЕЛЕНГАТОР | 1979 |
|
SU1015750A1 |
| ИЗМЕРИТЕЛЬ ФАЗЫ СИГНАЛОВ | 1989 |
|
RU2024883C1 |
| ТЕЛЕВИЗИОННЫЙ АДАПТИВНЫЙ ИЗМЕРИТЕЛЬ КООРДИНАТ | 1988 |
|
SU1623536A1 |
Изобретение относится к радиопеленгации. Устройство пеленгования с плоской антенной решеткой и неоднозначными фазовыми измерениями содержит антенные элементы 1, приемники 2, фазометры 3, весовые сумматоры 4, 6, 7, блоки 5 округления до целого, блоки 8 выделения остатков от округления до целого. 6 ил.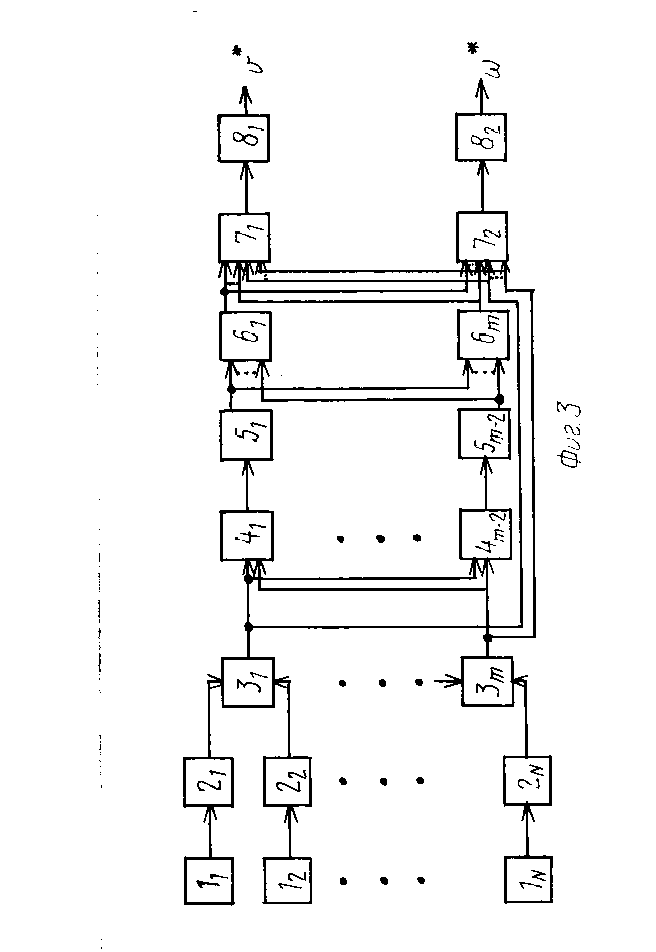
УСТРОЙСТВО ПЕЛЕНГОВАНИЯ С ПЛОСКОЙ АНТЕННОЙ РЕШЕТКОЙ И НЕОДНОЗНАЧНЫМИ ФАЗОВЫМИ ИЗМЕРЕНИЯМИ, содержащее N расположенных на плоскости антенных элементов, образующих m измерительных баз, N приемников, подключенных к выходам N антенных элементов, m фазометров, входами подключенных к выходам приемников m измерительных баз, отличающееся тем, что, с целью повышения достоверности пеленгования при произвольном размещении антенных элементов на плоскости в устройство введены m - 2 первых весовых сумматоров, m - 2 блоков округления до целого, m вторых весовых сумматоров, два третьих весовых сумматора и два блока выделения остатков от округления до целого, m входов m - 2 первых весовых сумматоров соответственно объединены и подключены к выходам m фазометров соответственно, выходы которых подключены соответственно к входам m - 2 блоков округления до целого, первые m входов двух третьих весовых сумматоров соответственно объединены и подключены к выходам m фазометров соответственно, m - 2 входа m вторых весовых сумматоров соответственно объединены и подключены к выходам m - 2 блоков округления до целого соответственно, вторые m входов двух третьих весовых сумматоров соответственно объединены и подключены к выходам m вторых весовых сумматоров, выходы двух третьих весовых сумматоров подключены соответственно к входам двух блоков выделения остатков округления до целого, выходы которых являются выходами устройства по двум переменным направлениям.
Авторы
Даты
1994-01-30—Публикация
1990-09-18—Подача