Изобретение относится к ускорительной технике и может быть использовано в научных исследованиях и при разработке новых типов ускорителей.
Известен способ ускорения заряженных частиц, основанный на взаимодействии пучка с продольным аксиальным полем стоячей электромагнитной волны, возбуждаемой в резонаторе с трубками дрейфа от двух генераторов с кратными частотами [1] .
Однако этот способ при достаточно хорошей моноэргетичности пучка и высоком коэффициенте захвата частиц пучка в режим ускорения практически сложен в реализации в связи с необходимостью применения дополнительных устройств и их согласования.
Известен способ ускорения заряженных частиц обратной пространственной гармоникой бегущей электромагнитной волны при фокусировке пучка однородным магнитным полем [2] .
Недостатком этого способа является сравнительно широкий энергетический спектр пучка, определяемый амплитудой электрического поля на выходе из ускорителя, где величина поля максимальна. Если теоретический коэффициент захвата частиц в режим ускорения при этом способе может быть доведен до величины 90% и более, то энергетический спектр ускоренного пучка составляет, например, порядка 10% относительно выходной энергии пучка электронов 10 МэВ [3] .
Целью изобретения является уменьшение величины энергетического спектра ускоряемого пучка.
Для достижения цели в способе ускорения заряженных частиц в однородном магнитном поле путем воздействия на них электрическим полем бегущей электромагнитной волны, фазовая скорость которой равна средней скорости пучка, на частицы одновременно с полем основной волны воздействуют электрическим полем дополнительной электромагнитной волны, круговая частота которой равна частоте основной волны, а отношения амплитуд и фазовых скоростей обеих волн удовлетворяют выражениям: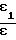 ≃ 1,
≃ 1,  = μ
= μ  + 1, где ε , Vo - соответственно амплитуда и фазовая скорость основной волны;
+ 1, где ε , Vo - соответственно амплитуда и фазовая скорость основной волны;
ε1, Vф - амплитуда и фазовая скорость дополнительной волны;
μ - удельный заряд частицы;
В - индукция магнитного поля;
ω - круговая частота волн.
Заявляемое техническое решение отличается от прототипа тем, что на пучок заряженных частиц одновременно воздействуют двумя волнами с одинаковой круговой частотой, но различными фазовыми скоростями. Это отличие определяет новизну способа. Данный отличительный признак не выявлен в других технических решениях в области ускорения заряженных частиц и, следовательно, обеспечивает заявляемому способу соответствие критерию "существенные отличия".
Отношение фазовых скоростей основной и дополнительной электромагнитных волн получено на основании следующего.
Пусть в канале ускорителя вдоль оси Z ускоряется пучок, взаимодействующий с электрическим полем электромагнитной волны амплитудой e, изменяющейся в частотой ω фазовая скорость которой равна средней скорости пучка Vo. Пучок фокусируется однородным магнитным полем В. Одновременно с основной волной в этом канале возбуждают дополнительную волну с той же частотой и амплитудой e1, фазовая скорость которой равна Vф. Электрическое поле суммы двух волн в канале ускорителя имеет вид: E = e ˙Io(Kr˙r)˙cosΦ+e1Io(κrr)cosϑ, (1) где Φ =  Z - ωt, Ψ =
Z - ωt, Ψ =  Z - ωt (2)
Z - ωt (2)
Φ, ϑ - фазы основной и дополнительной волн;
Io(. . . ) - функция Бесселя нулевого порядка,
Kr= 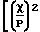 -
-  , κr =
, κr =  -
- 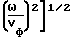 ,
,
р - период структуры; κ - вид колебаний;
r - расстояние частицы до оси канала.
В дальнейшем считаем, что Kr< κr и Io(Krr) ≃ 1.
Частицы пучка в магнитном поле двигаются по винтовой линии, вращаясь в поперечной плоскости с циклотронной частотой ωr= μB, где μ - удельный заряд частицы. Тогда расстояние произвольной частицы пучка до оси канала можно представить как функцию продольной координаты:
r = (R2+ ρ2 - 2R ρ cos Θ )1/2, (3) где R - среднее расстояние частицы до оси канала;
ρ - циклотронный радиус частицы, θ = 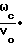 Z .
Z .
Разложим Io(. . . ) в ряд с учетом (3) по пространственным гармоникам оптической траектории частицы:
Io(κr·r) =  (-1)m·Io(κr·R)·Io(κrρ)·cosmθ, (4) где m = 0, ± 1, ± 2, . . . . Подставляем (4) в (1) и считаем, что для частиц пучка выполняются условия циклотронного резонанса при m = 1. Тогда можно пренебречь действием остальных членов ряда (4), кроме резонансного. Систему уравнений для скорости произвольной частицы пучка и фаз в этом случае можно записать в виде:
(-1)m·Io(κr·R)·Io(κrρ)·cosmθ, (4) где m = 0, ± 1, ± 2, . . . . Подставляем (4) в (1) и считаем, что для частиц пучка выполняются условия циклотронного резонанса при m = 1. Тогда можно пренебречь действием остальных членов ряда (4), кроме резонансного. Систему уравнений для скорости произвольной частицы пучка и фаз в этом случае можно записать в виде: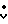 = εcosϕ + ε1cosΨ
= εcosϕ + ε1cosΨ
ϕ = v+1, 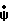 = gv-1-Ω, (5) где
= gv-1-Ω, (5) где
ε =  , ε1=
, ε1= 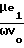 · I1(κrR)·I1(κrρ),
· I1(κrR)·I1(κrρ),
g = 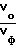 , Ω =
, Ω = 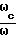 , v =
, v =  ,
,
ϕ = φ - KrR, Ψ = Ψ -  Z - κrR. При резонансе с обеими волнами
Z - κrR. При резонансе с обеими волнами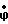 ≃ 0,
≃ 0, 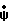 ≃ 0. (6) Решая совместно (6), имеет соотношение, выражающее в явном виде зависимость между фазовыми скоростями волн:
≃ 0. (6) Решая совместно (6), имеет соотношение, выражающее в явном виде зависимость между фазовыми скоростями волн: =
= 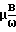 + 1. (7)
+ 1. (7)
Для обеспечения коэффициента захвата в режим ускорения, сравнимого с прототипом, отношение амплитуд дополнительной и основной волн должно быть 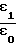 ≃ 0.
≃ 0.
П р и м е р 1. Проверка предлагаемого способа ускорения заряженных частиц проводилась методом численного моделирования. При  , μ = 108 Кл/кг, B = 9 Тл, ω = 108 c-1, непрерывном по фазе пучке в случае, когда амплитуда дополнительной волны была близка к нулю, энергетический спектр пучка имел вид, приведенный под номером 1 на чертеже. Здесь Δ N-количество частиц в интервале относительных энергий W =
, μ = 108 Кл/кг, B = 9 Тл, ω = 108 c-1, непрерывном по фазе пучке в случае, когда амплитуда дополнительной волны была близка к нулю, энергетический спектр пучка имел вид, приведенный под номером 1 на чертеже. Здесь Δ N-количество частиц в интервале относительных энергий W = 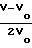 . Ширина спектра на полувысоте равнялась в этом случае 0,03.
. Ширина спектра на полувысоте равнялась в этом случае 0,03.
В случае воздействия на пучок дополнительной волны с амплитудой ε1 = 1 и равной основной при 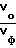 = 10 ширина спектра пучка на выходе из ускорителя составляла 0,006 (кривая 2).
= 10 ширина спектра пучка на выходе из ускорителя составляла 0,006 (кривая 2).
При 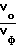 = 50 и всех остальных параметрах ускорителя тех же, что и в предыдущих случаях, ширина спектра еще уменьшалась и составляла 0,0016, т. е. почти в 20 раз меньше, чем для варианта, когда ускорение пучка производится одной волной. Коэффициент захвата частиц в режим ускорения с 78% , когда ускорение происходило основной волной, в последнем варианте увеличивался до 89% .
= 50 и всех остальных параметрах ускорителя тех же, что и в предыдущих случаях, ширина спектра еще уменьшалась и составляла 0,0016, т. е. почти в 20 раз меньше, чем для варианта, когда ускорение пучка производится одной волной. Коэффициент захвата частиц в режим ускорения с 78% , когда ускорение происходило основной волной, в последнем варианте увеличивался до 89% .
П р и м е р 2. Для получения спектра 3 (см. чертеж) электронного пучка с μ = 1,76.1011 Кл/кг частицы ускоряют в структуре встречно-штыревого типа, в которой внешним генератором возбуждают бегущие волны с круговой частотой ω = 7.109 с-1. Соотношение фазовых скоростей этих волн (основной и дополнительной) 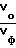 = 50. Частицы ускоряют в магнитном поле Б= 2 Тл. Одинаковость амплитуд обеих волн обеспечивают при размерах штырей вдоль оси пучка, сравнимых с длиной ускоряющих зазоров.
= 50. Частицы ускоряют в магнитном поле Б= 2 Тл. Одинаковость амплитуд обеих волн обеспечивают при размерах штырей вдоль оси пучка, сравнимых с длиной ускоряющих зазоров.
Таким образом при резонансном ускорении частиц двумя волнами имеется возможность существенного уменьшения энергетического спектра пучка. (56) 1. Авторское свидетельство СССР N 588888, кл. Н 05 Н 7/00, 1979.
2. Богомолов А. С. т. 208, N 6, 1973, с. 1328-1329. .
3. Богомолов А. С. , Бакиров Т. С. , Иванников В. И. и др. Письма в ЖТФ, т. 2, в. 1, 1976, с. 42-45.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИНДУКЦИОННОГО УСКОРЕНИЯ ИОНОВ | 2009 |
|
RU2420045C1 |
| СПОСОБ И УСТРОЙСТВО ОБНАРУЖЕНИЯ КОНТРАБАНДЫ | 2005 |
|
RU2300096C2 |
| ЛИНЕЙНЫЙ УСКОРИТЕЛЬ ЭЛЕКТРОНОВ | 2004 |
|
RU2282955C2 |
| СПОСОБ ИНДУКЦИОННОГО УСКОРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ | 2007 |
|
RU2359434C2 |
| СПОСОБ УСКОРЕНИЯ МАГНИТНЫХ ДИПОЛЕЙ | 2010 |
|
RU2442941C1 |
| Способ ускорения заряженных частиц | 1976 |
|
SU588888A1 |
| Способ бесконтактного измерения электромагнитных параметров материалов | 2015 |
|
RU2610878C1 |
| Авторезонансный СВЧ-генератор | 2017 |
|
RU2671915C2 |
| СПОСОБ УСКОРЕНИЯ МАКРОЧАСТИЦ | 2013 |
|
RU2523439C1 |
| СПОСОБ УСКОРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ И ЛИНЕЙНЫЙ УСКОРИТЕЛЬ | 2022 |
|
RU2792343C1 |

Использование: ускорительная техника. Сущность изобретения: при резонансном ускорении частиц в продольном магнитном поле двумя электромагнитными волнами - основной и дополнительной - обеспечивают одинаковую круговую частоту волн, а отношения их амплитуд и фазовых скоростей выбирают согласно выражениям, приведенным в описании. 1 ил.
СПОСОБ УСКОРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ в продольном магнитном поле путем воздействия на них электрическим полем электромагнитной волны, фазовая скорость которой равна средней скорости частиц, отличающийся тем, что на частицы одновременно с полем основной волны воздействуют электрическим полем дополнительной электромагнитной волны, круговая частота которой равна частоте основной волны, а отношения амплитуд и фазовых скоростей обеих волн удовлетворяют выражениям
ε1 / ε ≈ 1 , vо / vф = μ (B / ω ) + 1,
где ε , vо - амплитуда и фазовая скорость основной волны, м/с;
ε1 , vф - амплитуда и фазовая скорость дополнительной волы, м/с;
μ - удельный разряд частицы;
B - индукция магнитного поля, Тл;
ω - круговая частота волны, Гс.
Авторы
Даты
1994-05-30—Публикация
1991-07-02—Подача