Описание изобретения
Изобретение относится к области ускорительной техники и может быть использовано для решения научных и прикладных задач, в частности для создания потока искусственных микрометеоритов и в военном деле.
Область техники
Известен, [1], способ ускорения магнитных диполей одноступенчатым электромагнитным ускорителем. В силу одноступенчатости конечная скорость и, соответственно, энергия ускоренных магнитных диполей в нем мала.
Известен, [2], способ ускорения магнитных диполей многоступенчатым электромагнитным ускорителем, который, при использовании большого числа ступеней, в принципе, позволяет достичь большой конечной скорости магнитных диполей.
Недостатки прототипа
Однако прототип имеет принципиальный недостаток - движение магнитных диполей в нем неустойчиво в продольном направлении.
Дело в том, что при притяжении разноименных полюсов магнитов имеет место фазовая неустойчивость.
Так, если магнитный диполь (намагниченный железный стержень) немного отстанет от ускоряющего его бегущего токового импульса, то он будет оказываться во все меньшем поле импульса и, в конце концов, навсегда от него отстанет. Если же магнитный диполь излишне приблизится к импульсу тока, то он будет попадать во все большее поле, все сильнее притягиваться к импульсу, в конце концов, его обгонит и развернется на 180 градусов.
Измеряя в процессе ускорения скорость магнитного диполя, можно включить очередную катушку, например, с некоторой задержкой. Но это нельзя сделать, если магнитный диполь уже прилетел, а катушку надо было включить раньше. Это просто говорит о том, что бороться аппаратурными методами с фазовой неустойчивостью достаточно сложно.
Техническая задача, которую решает данный способ, состоит в устранении указанного недостатка, то есть создании условий, когда достигается фазовая (продольная) устойчивость ускоряемых магнитных диполей.
Сущность настоящего изобретения заключается в том, что магнитные диполи ориентируют в пространстве так, чтобы ось намагничивания совпадала с осью ускорения, и ускоряют полем бегущего токового импульса, при этом магнитные диполи предварительно ускоряют газодинамическим способом до скорости, соответствующей скорости инжекции, синхронную фазу выбирают на переднем склоне импульса, разворот диполей на 180 градусов в поле импульса предотвращают наложением внешнего однородного магнитного поля, по величине превосходящего поле импульса и противоположно к нему направленного, а радиальную фокусировку диполей осуществляют наложением внешнего магнитного поля, периодически изменяющегося в пространстве и по величине примерно равного полю импульса.
Связь отличительных признаков с положительным эффектом
С точки зрения взаимного расположения ускоряющего бегущего импульса и магнитного диполя, устойчивым является только случай, когда импульс толкает (а не тянет за собой) магнитный диполь. Это означает, что область фазовой (продольной) устойчивости находится на переднем склоне бегущего импульса.
Действительно, если магнитный диполь начнет опережать импульс и убежит вперед, то он будет попадать во все более слабое поле импульса, меньше ускоряться и, в конце концов, ускоренно бегущий импульс нагонит магнитный диполь. Если же магнитный диполь начнет отставать от импульса, то на его переднем склоне он начнет попадать во все более сильное поле и, в конце концов, вернется к своей фазе на импульсе, фазе, называемой синхронной.
Однако области фазовой устойчивости в азимутально-симметричной волне соответствует область радиальной неустойчивости. Магнитный диполь будет отталкиваться от одноименного полюса, но прежде всего он будет стремиться развернуться на 180° и притянуться к разноименному полюсу.
Разворот диполей на 180 градусов в поле ускоряющего импульса предотвращают наложением внешнего однородного магнитного поля, по величине превосходящего поле импульса и противоположно к нему направленного, а фокусировку диполей осуществляют наложением внешнего магнитного поля, периодически изменяющегося в пространстве и по величине примерно равного полю ускоряющего импульса.
Можно так же удерживать магнитный диполь от разворота на 180° и одновременно фокусировать его (удерживать его по радиусу вблизи оси ускорения) наложением только знакопеременного поля, не имеющего постоянной составляющей, что удобно делать с помощью постоянных магнитов.
При определенном выборе расстановки таких магнитов и напряженности поля в них движение магнитного диполя может быть устойчивым. Это означает, что магнитный диполь не только будет удерживаться от разворота знакопеременным полем, но и будет этим же полем удерживаться вблизи оси ускорения.
Осуществление изобретения. Работа устройства
1. Предварительное ускорение магнитных диполей газодинамическим методом
Для ускорения таких магнитных диполей полем бегущей волны - волна должна быть очень медленной. Надо сказать, что относительная скорость β=10-6 соответствует обычной скорости, равной: V=0.3 км/с, и она меньше скорости звука в воздухе. Газодинамический способ ускорения не позволяет достичь скорости, существенно превышающей скорость звука в воздухе. Например, технические характеристики пушки АП 35/1000, выпускаемой немецкой фирмой «Рейнметалл», таковы: начальная скорость стрельбы Vin=1.5 км/с, диаметр снаряда: dsh=35 мм. Фирма «Маузер» разрабатывает авиационную пушку с калибром (диаметром снаряда) dsh=30-35 мм и начальной скоростью снаряда Vin=1.8 км/с.
Для достижения малого коэффициента аэродинамического сопротивления магнитного диполя требуется форма диполя в виде длинного цилиндра с острым конусом в головной части. При этом, из-за малого диаметра магнитного диполя и большой его длины, трудно будет достичь такой начальной скорости Vin, как у авиационных пушек, поэтому, в нашем случае, начальную скорость магнитного диполя надо выбирать меньшей.
2. Выбор основных параметров
Выберем параметры ускоряемого диполя: диаметр D=2 мм, длина lcyl=70 мм, длина конусной части lcone=30 мм. Материал магнитного диполя - железо, начальная скорость магнитного диполя: Vin=0.6 км/с, конечная скорость магнитного диполя: Vfin=2 км/с, градиент магнитного поля в ускоряющем магнитный диполь импульсе выберем равным: ∂Hz/∂z=G=50 кГс/см, тогда длина ускорителя получится равной: L=25 метров.
Выберем угол наклона траектории магнитного диполя к горизонту: Θ=70°, при этом sinΘ=0.94, cosΘ=0.34. При отсутствии потерь скорости из-за аэродинамического сопротивления воздуха максимальная высота подъема магнитных диполей будет равна:
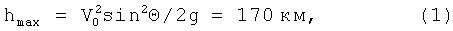
дальность полета:
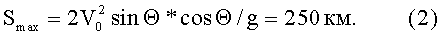
В отличие от ускорения электрически заряженных цилиндров, [3], где удельный заряд (Z/A) может регулироваться тем, что на цилиндре «размещается» различное число электронов, удельный магнитный момент железа постоянен и равен: m=2·10-10 эВ/(Гс·нуклон). Возьмем градиент магнитного поля ускоряющего диполи импульса равным: ∂Hz/∂z=50 кГс/см. В этом случае темп набора энергии магнитным диполем будет равен: ΔWsh=m·∂Hz/∂z=10-3 эВ / (м·нуклон), так, что для достижения прироста энергии, Wfin-Win, от энергии, соответствующей начальной скорости: Vin=0.6 км/с, до энергии, соответствующей конечной скорости, Vfin=2 км/с, Wfin-Win=2.5·10-2 эВ/нуклон, потребуется длина ускорения: L=(Wfin-Win)/ΔWsh=25 м.
Заметим, что, если магнитные диполи изготавливать в виде кольцевых сверхпроводящих рамок с током, то это позволит до 100 раз увеличить удельный магнитный момент, приходящийся на один нуклон, по сравнению с намагниченным железным стержнем.
3. Пути достижения требуемых параметров ускорителя
Перейдем теперь к определению параметров спирали, в которой должно произойти ускорение магнитных диполей с удельным магнитным моментом: m=2·10-10 эВ/Гс·нуклон от начальной скорости: βin=2·10-6 до конечной скорости: βfin=7·10-6, β=V/c, с=3·1010 см/с - скорость света в вакууме.
Радиусы спирали, [4], начальный и конечный возьмем равными: r0in=50 см, r0fin=30 см, начальное значение параметра х в этом случае будет равно: xin=6.28·50/(2·10-6·8·107)=2, конечное значение параметра х будет равно: xfin=6.28*30/(7·10-6·8·107)=0.34. Выбор длины волны λ0=8·107 означает, что мы выбрали длительность ускоряющего магнитного диполя импульса равной: (f0=с/λ0=375 Гц), τpulse=1/(2f0)=1.333 мс.
Замедленная длина волны равна: βλ0=2·10-6·8·107=160 см, и градиенту магнитного поля ∂Hzw/∂z=G=50 кГс/см, соответствует амплитуда магнитного поля импульса: Hzw=1.27 МГс. Эту амплитуду магнитного поля находят из соотношения: ∂Hzw/∂z=k3Bz=2πBz/βλ0. Откуда и получается значение: Hzw=βλ0·G/2π=1.27 МГс.
Чтобы найти мощность потока, необходимую для создания магнитного поля такой напряженности, найдем связь между компонентой электрического поля Ezw=E0I0(k1r) и магнитного поля 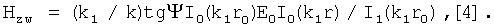 Для внутренней области спирали, где k1 - поперечный волновой вектор: k=(ω/с)·ε1/2 - волновой вектор, r0 - радиус спирали, выражение равно: (k1/k)=1/βф, tgΨ≈h/2πr0, так что (k1/k)·tgΨ=ε1/2, для начала спирали k1r0=2 и соотношение I0(k1r0)/I1(k1r0)=2. Таким образом, на оси спирали, компоненте магнитного поля Hzw=1.27 МГс соответствует напряженность электрического поля: Ezw≈5.37·106 В/см.
Для внутренней области спирали, где k1 - поперечный волновой вектор: k=(ω/с)·ε1/2 - волновой вектор, r0 - радиус спирали, выражение равно: (k1/k)=1/βф, tgΨ≈h/2πr0, так что (k1/k)·tgΨ=ε1/2, для начала спирали k1r0=2 и соотношение I0(k1r0)/I1(k1r0)=2. Таким образом, на оси спирали, компоненте магнитного поля Hzw=1.27 МГс соответствует напряженность электрического поля: Ezw≈5.37·106 В/см.
Значение скобки, {}, в формуле (13) работы [4] для значений аргумента xin=2 и xfin=0.34, 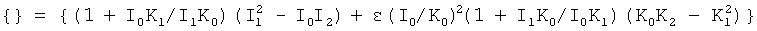
примерно одинаково и равно: {}=8, так, что требуемая мощность Р для достижения напряженности поля Ezw=5.37 МВ/см и для начальной скорости магнитного диполя βin=2*10-6, может быть найдена из формулы, [4]:
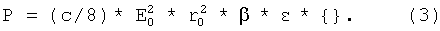
Мощность волны, выраженная в Ваттах, равна [4]:


Согласно формуле (4) для достижения градиента магнитного поля на оси поля G=50 кГс/см потребуются мощность: Р=6.4 ТВт. Такая мощность может быть достижима для импульсной техники.
Разложим синусоидальный импульс, [4], соответствующий полуволне Epulse=E0pulsesin(2π/T0)t, 2π/T0=ω0, ω0=2πf0 в ряд Фурье.
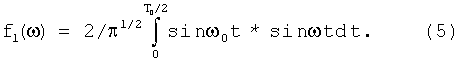
Спектр импульса достаточно узкий и занимает область частот от 0 до 2 ω0. Поскольку в спиральном волноводе дисперсия (зависимость фазовой скорости от частоты) слабая, можно ожидать, что весь спектр частот от 0 до 2ω0 будет распространяться примерно с одной и той же фазовой скоростью. В результате полуволновой синусоидальный импульс в пространстве будет расплываться в 3.5 раза только за счет увеличения фазовой скорости волны. Согласование спирального волновода с подводящим фидером в этом случае надо осуществлять в полосе частот: Δf≈ω0/2π.
Введем понятие амплитуды импульса 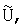 связанное с напряженностью поля на оси спирали Е0 соотношением [4]:
связанное с напряженностью поля на оси спирали Е0 соотношением [4]:
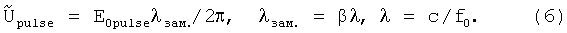
Напряжение импульса 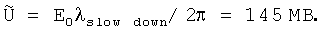 Ток
Ток 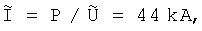 волновое сопротивление
волновое сопротивление 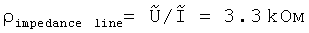 . Энергия импульса: Wp=¼·P·τ=1.2 ГДж, энергия магнитного диполя:
. Энергия импульса: Wp=¼·P·τ=1.2 ГДж, энергия магнитного диполя: 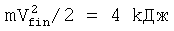 . В таблице собраны основные параметры ускорителя магнитных диполей.
. В таблице собраны основные параметры ускорителя магнитных диполей.
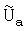
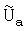 =145 MB
=145 MB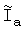
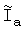 =44 kA
=44 kA
4. Предотвращение разворота диполя на 180° в магнитном поле импульса наложением однородного магнитного поля
Все было бы хорошо, если бы диполь был точечным. Но магнитный диполь не точка и действие со стороны радиальной компоненты магнитного поля приводит к «опрокидыванию», развороту диполя. Два взаимодействующих контура будут стремиться установиться так, чтобы их плоскости были параллельны друг другу, а направление обоих токов было одинаково. В отличие от «разностных» сил, ускоряющих диполь и приводящих к радиальному смещению центра тяжести, действие пары сил, приводящих к «развороту» диполя, суммируется.
Наиболее простым решением, препятствующим развороту на 180° диполя в ускоряющем поле волны, является наложение внешнего однородного магнитного поля, которое на процесс ускорения диполя влиять, в силу своей однородности, не будет, а будет лишь удерживать диполь от разворота в пространстве.
Наложим внешнее магнитное поле Hout на спираль с диполем, такое, чтобы оно удерживало рамку от переворачивания. Магнитное поле волны составляет величину порядка Hw=1.27 МГс, соответственно, для компенсации малых отклонений sinθ<<1 внешнее магнитное поле должно быть более Hout>3 МГс.
Таким образом, мы зафиксировали плоскость и направление (тока) в рамке. Разворачивающий момент теперь будет действовать на витки спирали, по которым течет импульсный ток, и их необходимо надежно закреплять. Можно рассматривать механическую модель такого ускорителя, которая должна состоять из двух магнитов, направленных друг к другу одноименными полюсами. Один из магнитиков - это намагниченный железный магнитный диполь. Второй магнитик - это импульс тока, бегущий по виткам спирали. Одноименные полюса магнитиков отталкиваются, импульс тока по виткам спирали бежит ускоренно и ускоряет (толкает) намагниченный магнитный диполь. От переворачивания толкаемый магнитик удерживает специальный узкий канал, (ствол) в котором он не может «развернуться». Толкающий магнитик так же не может «развернуться», он удерживается от разворота механическими силами.
Известно, что в однородном магнитном поле нет выделенной оси и однородное поле на диполь не действует, это означает, что магнитный диполь может смещаться в поперечном направлении под действием поля волны или просто из-за не нулевой начальной радиальной скорости.
Запишем формально уравнение радиального движения в виде:
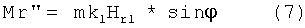
Угол отклонения магнитного диполя от оси
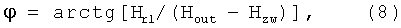
где Hr1 - радиальная компонента магнитного поля волны,
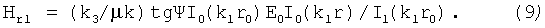
Учитывая, что центр диполя должен двигаться вблизи оси, будем считать Нr1 малым по сравнению с полем волны Hzw
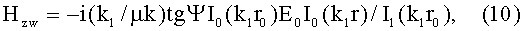
заменим Hr1=(k1r/2)Hzw, преобразуем формулу (10) для угла отклонения φ
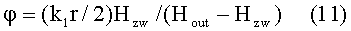
и преобразуем уравнение (7) к виду:
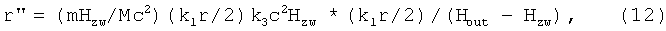
окончательно получим, заменяя k1 на k3 и mHzw/Mc2=Wλm.
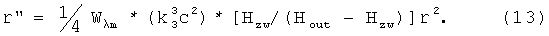
Линеаризуем уравнение (13), представим r=rbo+r1, тогда для r1 получим дифференциальное уравнение
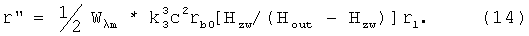
Выражение, стоящее перед радиусом r1 имеет смысл квадрата имкремента радиального движения:
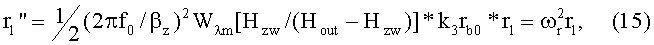
где
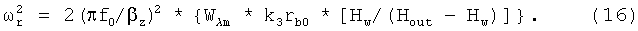
Как и в случае ускорения заряженных частиц, инкремент пропорционален частоте ускорения, однако для диполей он оказался много меньше, чем для заряженных частиц, где соответствующее выражение имеет вид, [4]:
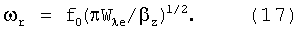
Это значит, что радиус магнитного диполя в секции нарастает экспоненциально. Возьмем начальный радиус влета магнитных диполей в секцию равным: rb0=0.1 см, начальную радиальную скорость примем равной нулю. Зависимость радиуса от времени тогда выглядит так:
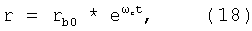
и это означает, что в отсутствие внешней фокусировки магнитный диполь будет отклоняться от оси полем волны. Подстановка численных значений в формулу (18) показывает, что инкремент нарастания радиального отклонения велик и надо вводить радиальную фокусировку.
5. Радиальная фокусировка магнитным полем, имеющим переменную составляющую
Чтобы исключить возможность «ухода» магнитных диполей по радиусу, надо ввести радиальную фокусировку. Проще всего это сделать, если наложить на внешнее однородное поле Hout дополнительное синусоидальное поле, так что суммарное поле будет представлять собой комбинацию постоянного поля Hout0, удерживающего рамку с током от «разворота», и переменной составляющей Hout1·sinkzZ, которая автоматически появится, если катушки соленоида, создающего продольное магнитное поле Hout, поставить достаточно редко. При этом kz=2π/az, где az - пространственный период расстановки катушек. Такой риппл, гофр Hout=Hout0+Hout1·sinkzZ магнитного поля приведет к появлению знакопеременного градиента внешнего магнитного поля и появлению знакопеременной силы в уравнении радиального движения, в предположении k⊥=kz
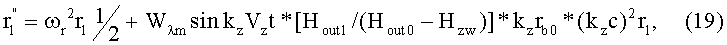
где kzVz - частота колебаний во внешнем магнитном поле.
Произведем замену переменных kzVzt=ωoutt=2τ. Тогда ∂/∂t=½ωout∂/∂τ и уравнение (19) можно записать в виде:
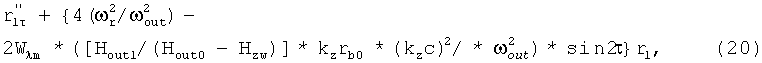
и уравнение поперечного движения сведется к уравнению Матье, [5]:
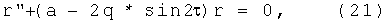
где
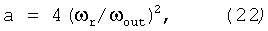
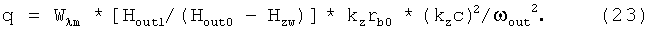
В зависимости от значения параметров а и q у уравнения Матье есть области устойчивых и неустойчивых решений. Выбирая расстановку катушек, формирующих магнитное поле (kz) и ток в них (Hout1) такими, чтобы решение уравнения (20) попадало в область устойчивости, можно будет получить устойчивое ускорение магнитных диполей. Условие устойчивости выглядит так, [5]: 0.92>q>a. После сокращения на Wλm, kzrb0, ωout 2 и (Hout0-Hw)-1 получим:
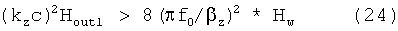
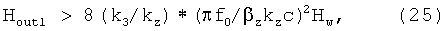
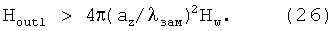
Подставляя цифры в последнее выражение: Hw=1.27 МГс, f0=375 Гц, βz=2·10-6, az=2π/kz, az≈r0=50 см - начальный радиус спирали, с=3·1010 см/с - скорость света в вакууме, получим:
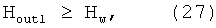
Для удержания магнитных диполей вблизи оси ускорения (радиальной фокусировки) переменная составляющая магнитного поля, удерживающего магнитные диполи от разворота на 180 градусов, должна составлять величину порядка поля волны.
Можно вообще исключить постоянное магнитное поле, а удержание диполя от разворота и удержание его по радиусу осуществлять только одним знакопеременным магнитным полем, не имеющим постоянной составляющей. Такое поле просто формировать на базе постоянных магнитов, аналогично тому, как это делается для фокусировки, например, электронных пучков в лампах бегущей волны. Такой результат получается, если амплитуда внешнего поля Hout будет в 2 раза превосходить поле импульса Hw, умноженное на отношение полупериода внешнего поля az к пространственной протяженности импульса lp: Hout>2(az/lp)Hw.
6. Затухание мощности при распространении импульса по спирали
Затухание волны в спиральном волноводе будет приводить к тому, что амплитуда распространяющегося по спирали импульса будет уменьшаться по мере движения импульса от начала к концу спирали и это уменьшение связано с омическими токами, идущими на нагрев спирали.
Ток Iφ протекает по виткам спирали и, собственно, омические потери это
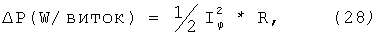
где Iφ - ток, текущий по витку в Амперах, R - сопротивление витка в Омах. Тогда ΔР/виток - будет выражено в Ваттах.
Найдем сначала сопротивление витка. Сопротивление вычисляется по обычной формуле: R=ρl/s, где р=1.7·10-6 Ом·см - удельное сопротивление меди, будем считать виток медным, 1=2πr0 - длина витка, r0 - радиус спирали. Поскольку ток, текущий по спирали, высокочастотный (переменный), появился множитель, ½ и такой ток проникает в проводник на глубину скин-слоя, которую и надо найти.
Выражение для глубины скин-слоя можно записать в виде:
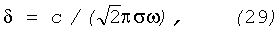
где с=3·1010 см/с - скорость света в вакууме, σ=5.4·10171/с - проводимость меди, ω=2πf0 - круговая частота, f0=375 Гц - частота волны, распространяющейся в спирали. Подстановка численных значений в формулу (29) дает: δ=0.34 см.
Получилась глубина скин-слоя, δ=0.34 см, много большая, чем расстояние между витками спирали h=1/n=0.02 см, n≈50 - число витков спирали, приходящихся на 1 см длины спирали. Это означает, что для уменьшения сопротивления одного витка и, соответственно, для уменьшения затухания наматывать спираль надо довольно широкой лентой, с шириной: Н=2δ=0.7 см. Ленту надо располагать широкой стороной Н по радиусу, с расстоянием между витками, например, h/2 так, чтобы из шага намотки h величину h/2 занимал виток и пространство h/2 было равно пробелу между витками.
Тогда сопротивление одного витка R=ρl/s будет равно:
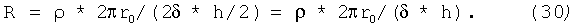
Подставляя численные значения для начала спирали r0=50 см, найдем
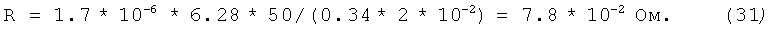
Теперь надо найти Iφ - ток, текущий по виткам. Для этого воспользуемся формулой
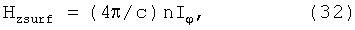
где Hzsurf - магнитное поле на поверхности спирали. Откуда ток, текущий по виткам спирали, nIφ может быть найден: nI φ(А/см)=Hzsurf/(4π/c)=(1.226)-1*Hzsurf(A/см)=Hzsurf (Гс.). Дальше - ток в одном витке равен:
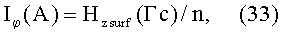
откуда ток в одном витке равен: Iφ(A)=[2.5 МА/см]/(50 витков/см)=50 кА/виток.
Подставляя это выражение в формулу (33), найдем, что омические потери тока в одном витке равны
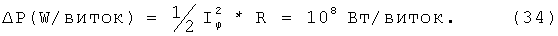
Поскольку на 1 см находится n витков, потери энергии на 1 см будут в n раз больше
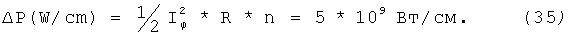
Введем соотношение
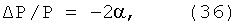
откуда
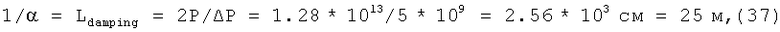
это длина, на которой напряженность поля уменьшится в е раз вследствие затухания. Видно, что движение магнитного диполя при ускорении надо рассчитывать с учетом затухания мощности импульса при его распространении по спиральному волноводу.
7. Захват магнитных диполей в режим ускорения. Допуска
Рассчитаем требуемую точность совпадения начальной ускоряющей объект фазы волны (импульса) с синхронной фазой. Теория захвата частиц в бегущую волну дает [6]: Δφ=3φs, (+φs-2φs). Реально это означает, например, в нашем случае, где λ/4 по длительности соответствует 300 мкс или 90°, что одному градусу по фазе примерно соответствует временной промежуток 3.3 мкс. В линейных ускорителях группирователь дает фазовую ширину сгустка +-15° и, чтобы не иметь больших фазовых колебаний, потребуем, чтобы точность синхронизации магнитного диполя с ускоряющим импульсом была: Δτ=+-15°=+-50 мкс. Такая точность синхронизации, по-видимому, вполне достижима для порохового старта - предварительного газодинамического ускорения магнитных диполей.
Рассчитаем теперь допуск на точность совпадения начальной скорости магнитного диполя и фазовой скорости распространяющегося по спиральной структуре импульса. Введем величину g=(p-ps)/ps - относительную разность импульсов [6]. В нерелятивистском случае - это просто относительный разброс скоростей g=(V-Vs)/Vs. Вертикальный размах сепаратрисы рассчитывается по формуле [6]:
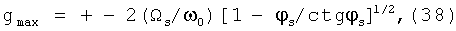
где φs=45°=π/4, ctgφs=1, [1-φs/ctgφs]1/2=0.46, 2*0.46=0.9, ω0=2πf0=2.35*103, Ωs/ω0=[Wλmctgφs/2πβs]1/2.
Определим величину: Wλm=(m∂Hz/∂z)λ0sinφs/Mc2 - относительный набор энергии магнитным диполем на длине волны λ0 в вакууме. В нашем случае: λ0=c/f0=8·107 см, sinφs=0.7, Мс2=1 ГэВ, Wλm=5.6·10-7, ctgφs=1. Подставляя численные значения, получим: g=(Vin-Vs)/Vs=ΔV/Vs и, наконец, ΔV/Vs=+-[5.6·10-7/(6.28·2·10-6)]1/2·0.9=+-0.19.
Таким образом, допустимое несовпадение начальной скорости магнитного диполя со скоростью импульса составляет величину порядка ΔV/Vs=+-20%.
Предложенный способ можно реализовать с помощью устройства
На Фиг.1 приведена схема устройства. Устройство состоит из пушки 1, где магнитные диполи 2 разгоняются до начальной скорости Vin=0.6 км/с. Полем высоковольтного токового импульса с напряжением: Uacc=145 MB, распространяющимся по секциям 3 спирального волновода с общей длиной L=25 метров, магнитные диполи ускоряют до конечной скорости Vfin=2 км/с. Энергия импульса составляет величину ~1.2 ГДж, переданная магнитным диполям энергия равна: 4 кДж, так, что их движение не искажает распространения импульса по спиральной структуре. Расположенными над секциями токовыми катушками 4, создающими магнитное поле: Hout0=3 МГс, магнитные диполи удерживают от разворота на 180°, этими же катушками создают периодическое изменение величины магнитного поля: Hout1≈1.3 МГс, этим, переменным по величине магнитным полем, ускоряемые магнитные диполи удерживают вблизи оси.
Возможное применение в военном деле.
1. Баллистика
Рассчитаем движение магнитного диполя, ускоренного электродинамическим способом и выпущенного под углом Θ к горизонту с учетом сопротивления воздуха. Уравнение движения магнитного диполя можно записать в виде:
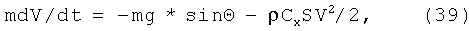
где m - масса диполя, V - скорость, g - 0.01 км/сек2 - ускорение силы тяжести, ρ=ρ0е-z/H - барометрическая формула изменения плотности атмосферы с высотой, ρ0=1.3*10-3 г/см3 - плотность воздуха у поверхности Земли, Н=7 км - значение высоты, на которой плотность падает в е раз, Θ - угол наклона траектории к горизонту, в нашем случае Θ=70°, sinΘ=0.9, cosΘ=0.34, S - поперечное сечение диполя, в нашем случае это магнитный диполь, S=πd2/4=3*10-2 см2, Сх - аэродинамический коэффициент.
Аэродинамическим коэффициентом или коэффициентом аэродинамического сопротивления называется безразмерная величина, учитывающая «качество» формы магнитного диполя.
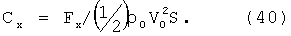
В нашем случае, поскольку начальная скорость V0=2 км/с, то второй член в уравнении (39) больше первого, то есть первым членом в уравнении (39), а именно mg*sinΘ, можно пренебречь, по сравнению со вторым.
Тогда уравнение (39) упрощается и выглядит так:
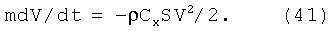
Решение уравнения (41) может быть записано в виде:
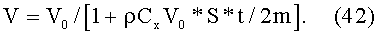
Для того чтобы можно было вычислять изменение скорости магнитного диполя со временем, необходимо найти аэродинамический коэффициент Сх.
2. Расчет коэффициента аэродинамического сопротивления диполей для воздуха
Будем считать, что магнитный диполь имеет форму цилиндрического стержня с конической головной частью. Тогда, при ударе молекулы азота по конусу, изменение продольной скорости молекул равно:
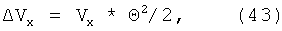
где Θ - угол конуса при вершине. Молекулы газа передают стержню импульс:
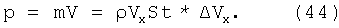
Изменение импульса в единицу времени - сила, сила лобового торможения.
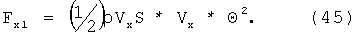
Разделив Fx1 на (½)ρV2 xS, получим коэффициент аэродинамического сопротивления для острого конуса при зеркальном отражении молекул от конуса (формула Ньютона):
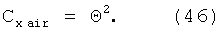
В нашем случае выбрано: Θ=1/15 и Cx air=4·10-3.
3. Прохождение магнитных диполей сквозь атмосферу
Проведем расчет прохождения магнитного диполя, имеющего коэффициент аэродинамического сопротивления Cx air=4·10-3, через атмосферу Земли. Уменьшение скорости со временем из-за сопротивления воздуха описывается формулой (42). Выберем следующие параметры: ρ=ρ0e-z/H, где Н=7 км, Cx air=4·10-3, S=3·10-2 см2, Vin=2·105 см/с, m=2 г, ρ0=1.3·10-3 г/см3. За первую секунду полета уменьшение скорости составит очень маленькую величину 7.8·10-3, меньшую одного процента.
В дальнейшем, с увеличением высоты подъема, вклад этого слагаемого будет экспоненциально уменьшаться. Так, для высоты подъема z=2 км, сомножитель е-z/H равен 0.75, для z=4 км равен 0.57 и т.д. Это означает, что потерей скорости, как при подъеме магнитного диполя, так и при спуске можно пренебречь и считать, что полет магнитного диполя проходит в безвоздушном пространстве. После спуска, вблизи поверхности Земли, скорость магнитного диполя будет примерно такой же, как и при старте: V0=2 км/с.
4. Глубина проникновения магнитных диполей в воду
При движении магнитного диполя в воде определяющей будет сила торможения, связанная с лобовым сопротивлением. В воде, в отличие от воздуха, отражение молекул от магнитного диполя надо считать диффузным, это приводит к коэффициенту аэродинамического сопротивления Сх water≈1. Зависимость уменьшения скорости от времени будет описываться формулой (42). Полагая, что второй член в знаменателе формулы (42) много больше первого (единицы), найдем путь, проходимый магнитным диполем до остановки:
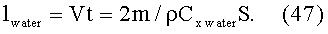
Подставляя в формулу (47) численные значения m=2 г, ρ=1 г/см3,
Cx water=1, S=3·10-2 см2, получим: lwater=1.3 метра.
5. Выводы
Максимальная высота подъема магнитных диполей, (1), h=170 км, получается выше траекторий полета самолетов и большей части ракет.
Дальность стрельбы, (2), Smax=250 км, такова, что с трех-четырех эсминцев, расположенных в Аденском заливе, можно простреливать весь залив.
Глубина проникновения в воду, (47), lwater=1.3 м, такова, что магнитными диполями можно обстреливать не только пиратов, но и легкие корабли.
Стоимость одного запуска ракеты Томагавк составляет 1 млн долларов.
Стоимость одного выстрела из rail gun составляет 1000 долларов.
Ожидаемая стоимость выстрела по данному способу может составить 1 выстрел/доллар.
Литература
1. Albert F. Reidi III, "Preliminary Investigation of an Electromagnetic Gun", NWL Technical Not No. TN-E-10/72, July 1972, Naval Weapon Laboratory, Dahlgren VA, 22448.
2. http://ru.wikipedia.org/wiki/Пушка_Гаусса
3. C.H.Доля, Способ ускорения макрочастиц, Заявка на изобретение №2010142684 от 20.10. 2010.
4. C.H.Доля, К.А.Решетникова, Об электродинамическом ускорении макроскопических частиц, Сообщение ОИЯИ, Р9-2009-110, Дубна, 2009, http://www1.jinr.ru/Preprints/2009/110%28P9-2009-110%29.pdf
5. Н.В.Мак-Лахлан, Теория и приложения функций Матье, Перев. с англ., Москва, Изд.-во иностр. лит., 1953.
6. И.М.Капчинский, Динамика частиц в линейных резонансных ускорителях, М.: Атомиздат, 1966.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УСКОРЕНИЯ МАГНИТНЫХ ДИПОЛЕЙ | 2011 |
|
RU2451894C1 |
| СПОСОБ УСКОРЕНИЯ МАКРОЧАСТИЦ | 2013 |
|
RU2523439C1 |
| СПОСОБ УСКОРЕНИЯ МАКРОЧАСТИЦ | 2012 |
|
RU2510603C2 |
| СПОСОБ УСКОРЕНИЯ МАГНИТНЫХ ДИПОЛЕЙ | 2012 |
|
RU2510164C2 |
| СПОСОБ УСКОРЕНИЯ МАКРОЧАСТИЦ | 2010 |
|
RU2456782C2 |
| СПОСОБ ЭЛЕКТРОСТАТИЧЕСКОГО УСКОРЕНИЯ МАКРОЧАСТИЦ | 2011 |
|
RU2455800C1 |
| СПОСОБ УСКОРЕНИЯ ТЕЛА | 2014 |
|
RU2558509C1 |
| СПОСОБ УСКОРЕНИЯ ЗАРЯЖЕННЫХ ЧАСТИЦ И ЛИНЕЙНЫЙ УСКОРИТЕЛЬ | 2022 |
|
RU2792343C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ПОДВОДНЫХ ОБЪЕКТОВ | 2012 |
|
RU2495448C1 |
| СПОСОБ ПОЛУЧЕНИЯ ПУЧКА ИОНОВ ВЫСОКОЙ ЗАРЯДНОСТИ | 2010 |
|
RU2448387C2 |
Изобретение относится к области ускорительной техники и может быть использовано для создания потока искусственных микрометеоритов и в военном деле. Ускорение магнитных диполей в данном способе осуществляют полем бегущего по спиральной структуре токового импульса. Магнитные диполи ускоряют газодинамическим способом до скорости, соответствующей скорости инжекции. Синхронную фазу выбирают на переднем склоне импульса. Разворот диполей на 180 градусов в поле импульса предотвращают наложением внешнего однородного магнитного поля, по величине превосходящего поле волны и противоположно к нему направленного. Фокусировку диполей осуществляют наложением внешнего магнитного поля, периодически изменяющегося в пространстве и по величине и примерно равного полю импульса. Изобретение позволяет создать условия, когда достигается продольная устойчивость ускоряемых магнитных диполей. 1 ил., 1 табл.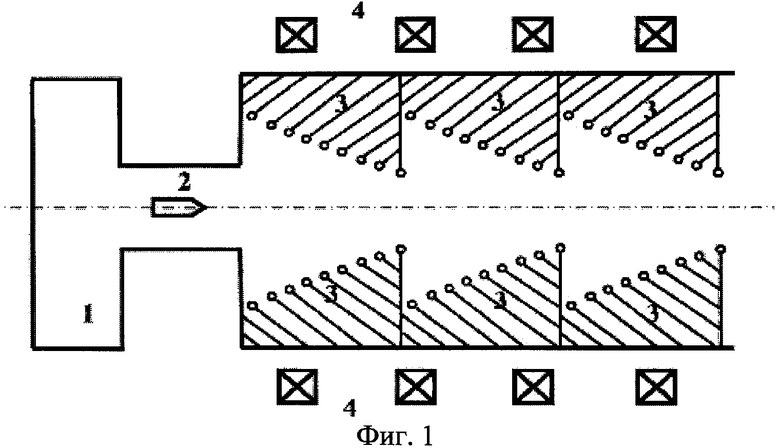
Способ ускорения магнитных диполей, заключающийся в том, что магнитные диполи ориентируют в пространстве так, чтобы ось намагничивания совпадала с осью ускорения и ускоряют полем бегущего токового импульса, отличающийся тем, что магнитные диполи предварительно ускоряют газодинамическим способом до скорости, соответствующей скорости инжекции, синхронную фазу выбирают на переднем склоне импульса, разворот диполей на 180° в поле импульса предотвращают наложением внешнего однородного магнитного поля, по величине превосходящего поле импульса и противоположно к нему направленного, а радиальную фокусировку диполей осуществляют наложением внешнего магнитного поля, периодически изменяющегося в пространстве и по величине примерно равного полю импульса.
| 0 |
|
SU89332A1 | |
| ЭЛЕКТРОМАГНИТНЫЙ УСКОРИТЕЛЬ МЕТАЕМОГО ТЕЛА | 2004 |
|
RU2267074C1 |
| УСТРОЙСТВО ДЛЯ УСКОРЕНИЯ ПРОВОДНИКОВ ПРИ ИСПЫТАНИЯХ МАТЕРИАЛОВ И ИЗДЕЛИЙ НА УДАРНОЕ ВОЗДЕЙСТВИЕ | 2000 |
|
RU2188377C2 |
| US 4922800 А, 08.05.1990 | |||
| Герметичный магнитоуправляемый контакт | 1973 |
|
SU448496A1 |
Авторы
Даты
2012-02-20—Публикация
2010-11-08—Подача