Описание изобретения
Изобретение относится к области ускорительной техники и может быть использовано для решения научных и прикладных задач, в частности для создания потока искусственных микрометеоритов.
Область техники
Известен, [1], способ ускорения макрочастиц - магнитных диполей, заключающийся в том, что магнитные диполи ориентируют в пространстве так, чтобы их ось намагничивания совпадала с осью ускорения, и ускоряют полем бегущего токового импульса, при этом внутри магнитных диполей создают дополнительный магнитный момент с помощью сверхпроводящей обмотки, расположенной внутри них с наружным диаметром Dout=2 cm, толщиной δsc=0.2 cm и длиной lsc=40 cm, и возбуждают в ней кольцевой ток с плотностью тока jsc=3*105 A/cm, а ускоряемые магнитные диполи имеют массу m=1 kg, диаметр Dsh=20 mm, полную длину ltot=65 cm, длину конусной части lcone=20 cm, магнитные диполи достигают конечной скорости Vfin=8.5 km/s и дальности полета Smax=12300 km при длине ускорения Lacc=2.27 km.
Однако этот способ ускорения макрочастиц имеет существенный недостаток. В течение всего времени ускорения и времени полета до цели, внутри магнитного диполя надо сохранять низкую температуру и поддерживать сверхпроводимость. Иначе, из-за большого выделения энергии внутри магнитного диполя он просто может разрушиться.
Известен, [2], способ ускорения макрочастиц, заключающийся в том, что макрочастицы предварительно ускоряют до скорости, соответствующей скорости инжекции в спиральный волновод, макрочастицы облучают пучком электронов, инжектированных из электронного ускорителя, электрически их заряжая, и окончательно ускоряют макрочастицы полем бегущего по виткам спирального волновода импульса напряжения, при этом макрочастицы имеют цилиндрическую форму с острым конусом в головной части, угол раствора конуса ©≈0.1, имеющим небольшую асимметрию, приводящую к созданию подъемной силы, Су=10-2, так что коэффициенты аэродинамического сопротивления Cx и подъемной силы Су примерно равны Cx≈Cy и по абсолютному значению составляют величину, много меньшую единицы, Cx Cy<<1.
Этот способ является наиболее близким к заявляемому способу ускорения макрочастиц и может быть выбран за прототип. Однако прототип имеет существенный недостаток, а именно низкий темп ускорения. Рассмотрим подробнее, какие ограничения присущи прототипу.
Недостатки прототипа:
1. Поверхностный барьер
Чтобы создать поверхностный барьер для электронов, «разместившихся» на макрочастице, нужно возможно больше увеличить работу выхода для электронов из макрочастицы. Наибольшей известной работой выхода обладает платина, пассивированная кислородом, [3], стр.445. Размещенный на макрочастице заряд будет с нее стекать путем автоэлектронной эмиссии, в соответствии с формулой, [3], стр.444.
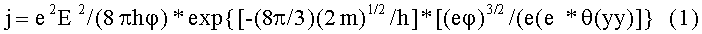
где θ(у) - функция Нордгейма, в которой аргументом является относительное снижение работы выхода внешним электрическим полем по Шоттки.
«Посадить» несколько зарядов на макрочастицу - не составит проблемы, но дальше, когда электронов на макрочастице будет много, они начнут стекать с нее за счет автоэлектронной эмиссии. Пусть напряженность поля для автоэлектронной эмиссии составляет: Е=3*107В/см. После достижения этой напряженности поля, сколько бы вы новых электронов ни сажали, они утекут с макрочастицы, собственно за счет кулоновского расталкивания.
После того как посажено достаточно много электронов, для того чтобы посадить последующие, надо преодолеть отталкивание тех, которые уже там сидят. И это значит, что энергия электронов, которые мы хотим посадить на макрочастицу, должна быть достаточно большой, такой, чтобы они могли преодолеть этот кулоновский барьер, долететь до макрочастицы и на ней остаться.
Кулоновский барьер растет для частиц цилиндрической формы линейно с ростом радиуса и для частиц с диаметром d=20 mm и будет достигать 30 MeV, так, что для его преодоления потребуется ускорять электроны в специальном ускорителе.
Определим заряд, который должен быть расположен на макрочастице, для создания напряженности электрического поля Esurf=3*107 V/cm, из выражения, связывающего напряженность поля на цилиндре с линейной плотностью заряда на нем:

откуда: Ne=1014, для диаметра цилиндрического стержня dr=20 mm.
Считая, что ускорение макрочастицы будет занимать достаточно большое время, τ≈2Lacc/Vfin, найдем, что для Lacc=10 km и Vfin=10 km/s это время составит: τ=2 s.
2. Утечка электронов
Найдем количество электронов, покинувших макрочастицу, за время ускорения. Для напряженности поля Е=30 MV/cm и работы выхода: еφ=6.5 eV из графика, [3], стр.461 найдем, что плотность тока утечки равна j30=10-9 A/cm2.
Утечка заряда ΔQ будет равна:
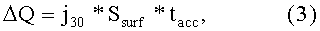
где j30=10-9 A/cm - ток утечки, Ssurf=6.28 cm - площадь боковой поверхности макрочастицы, tacc=2 s - время ускорения. Подставляя цифры в формулу (3), найдем, что ΔQ=6*1010 электронов и это составляет малую величину от числа электронов, посаженных на макрочастицу Ne=1014.
Для поверхностной напряженности электрического поля Esurf=40 MV/cm плотность тока утечки составляет: j40=10-4 A/cm2 утечка заряда (при постоянном электрическом поле) составила бы ΔQ=6*1015 электронов, это больше, чем размещено на цилиндре.
3. Число электронов, приходящихся на единицу массы
Чтобы найти заряд, приходящийся на единицу массы в таком стержне, а конкретно заряд, приходящийся на один нуклон, найдем число нуклонов на единице длины стержня из соотношения:

Площадь поперечного сечения равна, 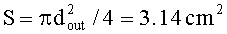
Найдем число электронов, приходящихся на нуклон в таком отрезке цилиндра единичной длины: (Z/A)e=(Ne/A)e=8.8*10-12, что является достаточно малой величиной для эффективного ускорения.
4. Длина ускорения
Действительно, для ряда практических применений целесообразно ускорять макрочастицы до скорости Vfin=8.5 km/s, которой соответствует энергия, приходящаяся на нуклон, равная:
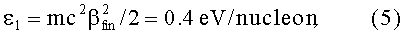
где βfin=Vfin/c=2.83*10-5 - скорость макрочастицы, выраженная в единицах скорости света в вакууме, с=3*1010 cm/s. Тогда в электрическом поле с напряженностью Ezw0*sinφs=250 kV/cm, где sinφs=0.7, φs=45° - синхронная фаза, темп ускорения будет равен:

и для достижения конечной энергии ε1=0.4 eV/nucleon потребуется длина Lacc1=ε1/ΔW1=1.8*103 m=1.8 km. Такая большая длина ускорения, Lacc1=1.8 km, получается именно из-за низкого темпа ускорения макрочастиц.
Таким образом видно, что прототип с ростом диаметра макрочастиц имеет все более низкий темп ускорения и для достижения требуемой конечной скорости макрочастиц требуется все большая длина ускорения.
Техническая задача изобретения состоит в устранении указанных недостатков, а именно в увеличении темпа набора энергии макрочастицами при ускорении в спиральном волноводе.
Ускорение электрических диполей
Сущность предложенного способа состоит в том, что в способе ускорения макрочастиц их предварительно электрически заряжают, предварительно ускоряют газодинамическим способом до скорости, соответствующей скорости инжекции в спиральный волновод, и окончательно ускоряют полем бегущего по виткам спирального волновода импульса напряжения, при этом, что в качестве макрочастиц используют плоский конденсатор, который ускоряют полем бегущего по виткам импульса напряжения с темпом ускорения ΔW/Δz=(Ne/A)e*(2πdd/λs)*Ezw0*sinφs, где ΔW/Δz - набор энергии плоским конденсатором на единице длины, eNe/A - электрический заряд какого-либо знака, расположенный на плоском конденсаторе и приходящийся на один нуклон в нем, dd - расстояние между обкладками плоского конденсатора, λs - длина волны ускорения в спиральном волноводе, Ezw0 - амплитуда волны, φs - синхронная фаза, при этом ускорение плоского конденсатора ведут в диэлектрическом канале, предотвращая его разворот на 180 градусов и его отклонение от оси ускорения.
Связь отличительных признаков с положительным эффектом
На макрочастице можно разместить большое количество связанных зарядов, то есть зарядов противоположных знаков и, таким образом, получить электрический диполь, если выбрать макрочастицу в виде плоского конденсатора. При этом общий электрический заряд, размещенный на макрочастице, будет равен нулю, но у такой макрочастицы будет достаточно большой электрический дипольный момент, который может взаимодействовать с градиентом электрического поля.
1. Параметры электрического диполя
Рассмотрим ускорение цилиндрического конденсатора с наружным диаметром dout=2 cm, расстояние между обкладками которого равно:
dd=1 cm, где в качестве диэлектрика используется конденсаторная керамика Т-900, с относительной диэлектрической проницаемостью ε=1000 и пробивным напряжением U=28 kV/mm, [3], стр.321. Будем считать плотность конденсаторной керамики равной: ρ=6 g/cm3, [4].
Найдем удельный электрический заряд такого конденсатора, при этом массой собственно металлических обкладок пренебрежем. Площадь и объем диэлектрика равны: 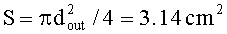
Найдем электрический заряд, находящийся на конденсаторе. Емкость плоского конденсатора в практической системе координат равна:
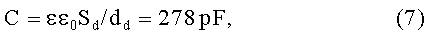
где ε0=8.85*10-12 F/m - диэлектрическая проницаемость вакуума. Такой конденсатор можно зарядить до 280 kV, [3], стр.321, так, что электрический заряд (выраженный в практических единицах) на нем будет:
Q=CU=7.8*10-5 Coulomb, (8)
то есть конденсатор будет содержать:
Ne=7.8*10-5*6*1018=4.7*1014электронов.
Число нуклонов в таком цилиндре равно: А=1.13*10 нуклонов, отношение заряда к массе в таком конденсаторе, таким образом, равно: (Ne/A)e=4.1*10-11. Таким образом, количество электронов, приходящихся на один нуклон, в таком плоском конденсаторе много больше, чем число электронов, приходящихся на нуклон в электрически заряженном стержне, (Ne/A)e=8.8*10-12, имеющем такие же размеры.
2. Ускорение диполей
Ускорение электрического диполя осуществляется градиентом электрического поля волны, аналогично тому, как градиент магнитного поля ускоряет магнитный диполь
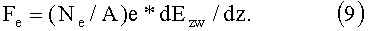
Так же как для магнитного диполя, градиент электрического поля волны равен dEzw/dz=k3*Ezw, k3=2π/λs, где λs=λ0*φph - замедленная длина волны в структуре, βph=Vph/c - относительная фазовая скорость волны в спиральном волноводе.
Окончательно,
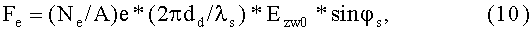
где Ezw0 - амплитуда напряженности электрического поля на оси спирали.
Прежде чем подставлять цифры в формулу (10), сделаем несколько общих замечаний.
Отметим, прежде всего, независимость ускоряющей электрические диполи силы Fe от физической длины диполя dd. Действительно, с уменьшением dd растет емкость С плоского конденсатора, но одновременно уменьшается пробойное напряжение U, так что заряд, запасенный в конденсаторе от параметра dd, не зависит.
С уменьшением параметра dd уменьшается масса диэлектрика и удельный электрический заряд, заряд, приходящийся на единицу массы, растет. Однако с уменьшением dd уменьшается ускоряющая сила, Fe, действующая на диполь. Это связано с тем, что ускоряющая сила является разностью между силой отталкивания одного полюса и силой притяжения другого полюса. Из формулы (10) видно, что эта сила тем больше, чем больше расстояние dd между полюсами диполя.
Более того, ускоряющая сила, действующая на электрический диполь, не зависит от величины Sd - поперечной площади диполя. Действительно, с ростом этой площади растет запасенный в конденсаторе заряд, но одновременно в этой же пропорции растет масса диэлектрика. Это приводит к независимости удельного электрического заряда конденсатора от его поперечного сечения. Надо сказать, что в случае магнитного диполя ситуация иная. Магнитный момент витка с током растет как площадь витка, то есть квадратично с ростом радиуса, масса же витка растет как периметр витка, то есть линейно с ростом радиуса, что приводит к линейному росту удельного магнитного момента с ростом радиуса витка с током.
Подставим теперь цифры в формулу (10). Первый сомножитель (Ne/A)e определяет тот максимальный электрический заряд, приходящийся на один нуклон, который можно запасти в конденсаторе. Как было показано выше, он определяется только свойствами вещества, в данном случае конденсаторной керамики, а именно максимально возможными относительной диэлектрической проницаемостью ε и максимальным пробивным напряжением U. Возможно, со временем, будут разработаны материалы с лучшими характеристиками.
Второй сомножитель 2πdd/λs определяется отношением физической длины диполя dd к замедленной длине волны λs в спиральном волноводе. При большой длине ускорителя весь ускоритель нужно будет разбивать на отдельные секции, каждая из которых будет иметь индивидуальное питание. Тогда можно будет вести ускорение на оптимальной для каждой секции частоте, которая для случая спирального волновода определяется соотношением: λs=2πr0, где r0 - радиус спирали. Диаметр спирали может быть выбран несколько большим, чем dout - диаметр конденсатора, например: dout/2r0=0.5, при этом параметр равен: dd/r0=0.5.
Окончательно,

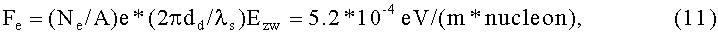
так, что для достижения той же конечной скорости потребуется длина ускорения, равная:
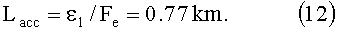
Осуществление изобретения
Работа устройства
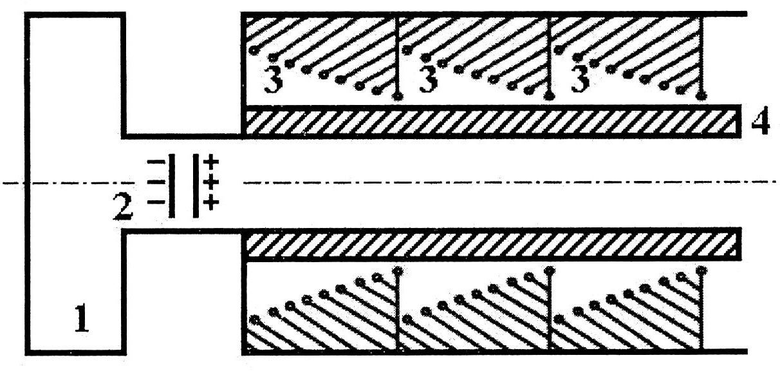
На Фиг.1 приведена схема устройства: 1 - пушка, осуществляющая газодинамическое ускорение макрочастиц, 2 - макрочастицы, предварительно заряженные электрические конденсаторы, 3 - секции спирального волноводы, 4 - диэлектрический канал, расположенный на оси системы, в котором осуществляется ускорения макрочастиц.
1. Предварительное ускорение макрочастиц газодинамическим методом
Для ускорения макрочастиц полем бегущей волны волна должна быть очень медленной. Надо сказать, что относительная скорость β=10-6 соответствует обычной скорости, равной: V=0.3 km/s и она меньше скорости звука в воздухе. Газодинамический способ ускорения не позволяет достичь скорости, превышающей скорость Vg=2 km/s. Например, технические характеристики пушки АП 35/1000, выпускаемой немецкой фирмой «Рейнметалл», таковы: начальная скорость стрельбы Vin=1.5 km/s, диаметр снаряда: dsh=35 mm. Фирма «Маузер» разрабатывает авиационную пушку с калибром (диаметром снаряда) dsh=30-35 mm и начальной скоростью снаряда Vin=1.8 km/s.
Примем начальную скорость макрочастицы, достигнутую после равной Vin=1 km/s.
Возможно, впрочем, использование подкалиберного снаряда позволит достичь большей начальной скорости, чем мы предполагаем. Так же, при скорости снаряда Vsh равной Vsh=2 km/s динамическое противодавление со стороны воздуха, находящегося в стволе пушки, составляет 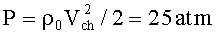
2. Шаг спирали
Поскольку мы выбрали радиус спирали равным: r0=2 cm, то чтобы получить в этой спирали замедление равное βph in=3.3*10-6, где βph in=Vin/c - начальная фазовая скорость, выраженная в единицах скорости света и совпадающая с начальной скоростью макрочастицы, потребуется очень мелкий шаг намотки спирали.
Замедление в спирали является чисто геометрическим, в простейшем случае фазовая скорость волны, выраженная в единицах скорости света в спиральном волноводе, как известно, равна:
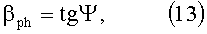
где tgψ - тангенс угла намотки, тангенс, в случае больших замедлений равен: tgψ=h/2πr0 - отношению шага намотки спирали к периметру витка.
Кроме чисто геометрического замедления волны в спирали можно волну дополнительно замедлить, если спираль целиком поместить внутрь диэлектрической среды с относительной диэлектрической проницаемостью ε. Для титаната бария, вблизи точки Кюри, достижимы значения ε=8*103, [5], стр.557. Примем для ε несколько меньшее значение: ε=1.28*103. Связь между фазовой скоростью волны, распространяющейся в спирали, и ее параметрами в этом случае можно записать в виде, [6],
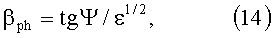
Область, находящуюся внутри спирали, надо оставить свободной от диэлектрика, в этой области, по оси спирали, будет происходить ускорение макрочастиц. Тогда для спирали, у которой диэлектриком заполнена область, расположенная между спиралью и внешним экраном, дисперсионное уравнение - уравнение, связывающее параметры спирали с фазовой скоростью волны, выглядит так, [6],
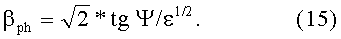
Для начала спирали, где скорость макрочастицы равна Vin=1 km/s, βph in=3.3*106, r0=2 cm, ε=1.28*103, найдем из (15), что шаг намотки спирали должен быть равен:

Амплитудная напряженность поля Ezw0, выбранная нами, равна: Ezw0=Ezw/sinφs=350 kV/cm. При шаге h=10-3 cm=10µ возникает опасность межвиткового пробоя диэлектрика. Пробивное напряжение полиимида достигает 300 MV/m [5], стр.550, или 300 V/µ, так, что можно выбрать структуру спирали следующей: медный виток с поперечным сечением 8µ и изоляцию из полиимида, толщиной в 2 микрона.
3. Потребная мощность волны
Связь, между потоком мощности и напряженностью поля волны на спирали, дается формулой, [6],
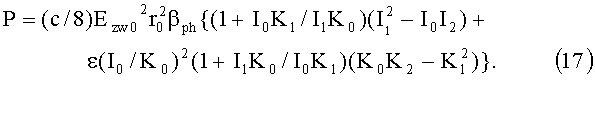
Аргументом модифицированных функций Бесселя первого и второго рода, стоящих в фигурных скобках, является величина х=2πr0/λs, которую мы выбрали равной: x=1. Тогда для этого аргумента второе слагаемое в фигурных скобках много больше первого, а сама фигурная скобка равна: {}=3.77*ε. Подставляя цифры в формулу (17), найдем,
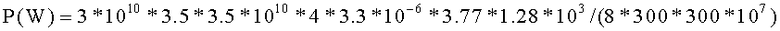
что для того чтобы напряженность поля на оси спирали была равна Ezw0=350 kV/cm, в нее требуется ввести мощность: P=125 MW.
Такая мощность может быть достижима для импульсной техники.
Разложим синусоидальный импульс, [6], соответствующий полуволне Epulse=E0PulseSin(2π/T0)t, 2π/Т0=ω0, ω0=2πf0 в ряд Фурье.
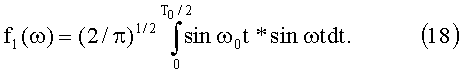
Спектр импульса достаточно узкий и занимает область частот от 0 до 2ω0. Поскольку в спиральном волноводе дисперсия (зависимость фазовой скорости от частоты) слабая, можно ожидать, что весь спектр частот от 0 до 2ω0 будет распространяться примерно с одной и той же фазовой скоростью. В результате полуволновой синусоидальный импульс в пространстве будет расплываться только за счет увеличения фазовой скорости волны. Согласование спирального волновода с подводящим фидером в этом случае надо осуществлять в полосе частот: Δf≈ω0/2π.
Введем понятие амплитуды импульса Uacc, связанное с напряженностью поля на оси спирали Ezw0 соотношением, [6]:

В нашем случае длина волны в вакууме λ0 равна:
λ0=λs/βin=4.18*106 cm, частота волны: f0=c/f0=7.1*103 Hz, полупериод - длительность импульса по основанию равна: T0/2=1/2f0=90 µs.
Таким образом, амплитуда импульса напряжения, распространяющегося по спирали, должна быть равна: Uacc=Ezw0*λs/2ρ=700 kV. В Таблице собраны основные параметры ускорителя.
конечная, β=βph
2.83*10-5
4. Затухание мощности при распространении импульса по спирали
Затухание волны в спиральном волноводе будет приводить к тому, что амплитуда распространяющегося по спирали импульса будет уменьшаться по мере движения импульса от начала к концу спирали и это уменьшение связано с омическими токами, идущими на нагрев спирали.
Ток Iφ протекает по виткам спирали и, собственно, омические потери это:
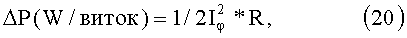
где Iφ - ток, текущий по витку в амперах, R - сопротивление витка в омах. Тогда ΔP/виток - будет выражено в ваттах.
Найдем сначала сопротивление витка. Сопротивление вычисляется по обычной формуле: R=ρl/s, где ρ=1.7*10-6 Ohm*cm - удельное сопротивление меди, будем считать виток медным, l=2πr0 - длина витка, r0 - радиус спирали, s - поперечное сечение витка. Поскольку ток, текущий по спирали, высокочастотный (переменный), появился множитель, Ѕ и такой ток проникает в проводник на глубину скин-слоя, которую и надо найти.
Выражение для глубины скин-слоя можно записать в виде:
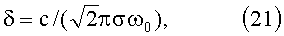
где с=3*1010 cm/s - скорость света в вакууме, σ=5.4*1017 l/s - проводимость меди, ω0=2πf0 - круговая частота, f0=7.1*103 Hz - частота волны, распространяющейся в спирали. Подстановка численных значений в формулу (21) дает: δ=7.7*10-2 cm.
Получилась глубина скин-слоя, δ=7.7*10-2 cm, много большая, чем расстояние между витками спирали h=1/n=10-3 cm, где n≈103 - число витков спирали, приходящихся на 1 cm длины спирали. Это означает, что для уменьшения сопротивления одного витка и, соответственно, для уменьшения затухания, наматывать спираль надо довольно широкой лентой, с шириной: Н=2δ=0.15 cm. Ленту надо располагать широкой стороной Н по радиусу, с расстоянием между витками 10 µ, как было сказано выше, толщина собственно ленты 8 µ и 2 µ толщина полиимидной изоляции, покрывающей медную ленту.
Тогда сопротивление одного витка R=ρl/s будет равно:
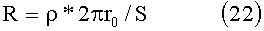
Подставляя численные значения для начала спирали r0=2 cm, найдем
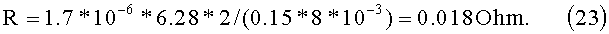
Теперь надо найти Iφ - ток, текущий по виткам. Для этого воспользуемся формулой:
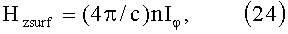
где Hzsurf - магнитное поле на поверхности спирали.
Найдем связь между компонентой электрического поля Е0 на оси спирали и компонетной магнитного поля Hz на поверхности спирали: Hzsurf=(k1/k)tgψI0(k1r0)E0I0(k1r)/I1(k1r0), [6]. Для внутренней области спирали, где k1 - поперечный волновой вектор: k=(ω/с)*ε1/2 - волновой вектор, r0 - радиус спирали, выражение равно: (k1/k)=1/βph, tgψ=h/2πr1, так что (k1/k)*tgψ=ε1/2. Для k1r0=1 соотношение I0(k1r0)/I1(k1r0)=2.
Таким образом, компоненте электрического поля: Е0≈350 kV/cm, на оси спирали, соответствует напряженность магнитного поля Hzsurf=83 kGs на поверхности спирали.
Теперь можно найти ток, текущий по виткам спирали, Ток nIφ может быть найден из соотношения: nIφ(А/ст)=1.226*Hzsurf=100 kA/cm. Ток в одном витке равен:
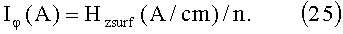
Подставляя численные значения в формулу (25), что ток в одном витке равен: Iφ(А)=[100 kA/cm]/(103 витков/cm)=100 А/виток.
Омические потери тока в одном витке равны:
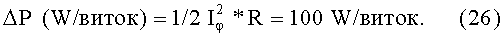
Поскольку на 1 cm находится n витков, потери энергии на 1 cm будут в n раз больше:
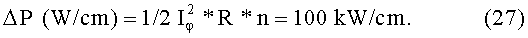
Введем соотношение:

откуда
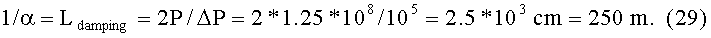
Это длина, на которой напряженность поля уменьшится в е раз вследствие затухания. Видно, что при ускорении частицы затухание мощности импульса при распространении мощности по спиральному волноводу можно не учитывать.
5. Захват макрочастиц в режиме ускорения, допуска
Рассчитаем требуемую точность совпадения начальной ускоряющей объект фазы волны (импульса) с синхронной фазой. Теория захвата частиц в бегущую волну дает, [7]: Δφ=3φs, (+φs-2φs). Реально это означает, например, что в нашем случае, где Т0/4 по длительности соответствует 45 µs или 90°, что одному градусу по фазе примерно соответствует временной промежуток 0.5 µs. В линейных ускорителях группирователь дает фазовую ширину сгустка ±15° и, чтобы не иметь больших фазовых колебаний, потребуем, чтобы точность синхронизации макрочастицы с ускоряющим импульсом была: Δτ=±15*0.5 µs=±7 µs. Такая точность синхронизации, по-видимому, вполне достижима для порохового старта - предварительного газодинамического ускорения макрочастиц.
Рассчитаем теперь допуск на точность совпадения начальной скорости макрочастицы и фазовой скорости распространяющегося по спиральной структуре импульса. Введем величину g=(p-ps)/ps - относительную разность импульсов, [7]. В нерелятивистском случае - это просто относительный разброс скоростей g=(V-Vs)/Vs. Вертикальный размах сепаратрисы рассчитывается по формуле, [7]:
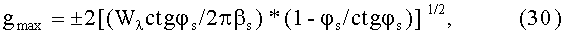
где φs=45°=π/4, ctgφs=1, [1-φs/ctgφs]1/2=0.46, 2*0.46=0.9, Wλ=(Z/A)eE0λ0sinφs/Mc2.
Определим величину: Wλ=(2πd/λs)*(Z/A)eE0λ0sinφs/Mc2 - относительный набор энергии макрочастицей на длине волны λ0 в вакууме. В нашем случае: λ0=c/f0=4.18*106 cm, sinφs=0.7, Мс2=1 GeV, Wλ=2.1*10-8. Подставляя численные значения, получим: g=(Vin-Vs)/Vs=ΔV/Vs и, наконец, ΔV/Vs=±[2.1*10-8/(6.28*3.3*10-6)]1/2*0.9=±0.09.
Таким образом, допустимое несовпадение начальной скорости макрочастицы со скоростью импульса составляет величину порядка: ΔV/Vs=±9%. Для начальной скорости макрочастицы Vin=1 km/s допуск на отклонение скорости составляет ΔV<90 m/s.
6. Автофазировка
Известно, [7], в бегущей волне область фазовой устойчивости находится на переднем склоне волны, импульса. Действительно, если частица будет обгонять волну, она будет попадать в область все более слабого поля и, в конце концов, ускоренно бегущий импульс догонит частицу.
Если же частица будет отставать от бегущего импульса, она будет попадать в область все более сильного поля, будет приобретать большую энергию по сравнению с той, которую она приобретала бы находясь в синхронной фазе, и, в конце концов, частица догонит волну и вернется к своей синхронной фазе φs.
Таким образом, с точки зрения взаимного расположения частицы и ускоряющего импульса возможен только случай, когда импульс «толкает, а не «тянет» частицу. В наших расчетах мы выбрали синхронную фазу равной φs=45°, sinφs=0.7, для достижения большего темпа ускорения можно выбрать и большее значение φs=60°, sinφs=0.87, но тогда при ускорении придется выдерживать более жесткие допуска.
Известно, [7], что при ускорении частиц в азимутально-симметричном поле области фазовой устойчивости соответствует радиальная неустойчивость. Это означает, что когда мы толкаем импульсом частицу, мы толкаем ее не только вперед, но и немного по радиусу. Сила, действующая на частицу, линейно возрастает с ростом отклонения частицы от оси и начальное отклонение экспоненциально возрастает.
Для удержания частицы вблизи оси при ускорении надо вводить фокусировку, то есть надо использовать дополнительные силы поля, которые будут возвращать частицу к оси ускорения.
7. Предотвращение разворота диполя на 180° в электрическом поле импульса и удержание диполя вблизи оси ускорения
При ускорении диполей появляется новая проблема, которой не было при ускорении точечных частиц, а именно ускоряющий диполь импульс будет приводить к опрокидыванию диполя, то есть к его развороту на 180 градусов.
Это легче всего можно видеть при ускорении магнитных диполей, обычных магнитиков, бегущим токовым импульсом. Если такой импульс, толкающий магнитик, заменить другим магнитиком, то можно видеть, что толкаемый магнитик будет не просто отталкиваться от одноименного полюса толкающего магнитика, но будет стремиться развернуться на 180 градусов и притянуться к противоположному полюсу.
В отличие от «разностных» сил, ускоряющих диполь и приводящих к радиальному смещению центра тяжести, действие пары сил, приводящих к «развороту» диполя, суммируется.
Наиболее простым решением, препятствующим развороту на 180° магнитных диполей в ускоряющем поле волны, является наложение внешнего однородного магнитного поля, которое на процесс ускорения диполя влиять, в силу своей однородности, не будет, а будет лишь удерживать диполь от разворота в пространстве, [1].
По аналогии с однородным магнитным полем, не влияющим на процесс ускорения диполей, а только удерживающим магнитные диполи от разворота на 180 градусов, можно использовать однородное электрическое поле для удержания от разворота электрического диполя.
Напряженность такого электрического поля должна быть по крайней мере большей амплитуды волны, то есть Ekeep>350 kV/cm. При длине ускорения Lacc≈1 km электростатическое поле для этой цели не подходит, поскольку в этом случае пришлось бы иметь гигантскую разность потенциалов.
Однородное электрическое поле можно создать индукционным способом. Пусть длина индуктора равна (вдоль оси ускорения) lind=10 cm. Такую длину макрочастица, имеющая скорость Vin=1 km/s, пролетит за время τind=10-4s, следовательно, индукционным способом надо создать напряжение Uind=Ekeep*lind=3.5 MV на время τind=10-4s.
Перемножая эти величины, найдем, что требуемый магнитный поток составляет величину Ф=350 Т*m2. Пусть этот поток создается перемагничиванием железа от значения -1 Т до значения +1 Т, тогда площадь сечения железа в индукторе должна составлять Sind=175 m2 и, при длине индуктора вдоль оси ускорения lind=10 cm его радиальная протяженность должна составлять: rind=1750 m, что также не разумно.
Удерживать макрочастицы вблизи ускорения и одновременно удерживать их от разворота на 180 градусов можно, если вести ускорение макрочастицы в узком диэлектрическом канале, расположенном на оси системы.
8. Влияние сил трения
Рассмотрим, насколько трение боковой поверхности макрочастицы по внутренней поверхности канала будет влиять на процесс ускорения.
Боковая поверхность макрочастицы должна быть диэлектрической, чтобы по ней не было замыкания конденсатора, канал также должен быть диэлектрическим, чтобы он не экранировал ускоряющее макрочастицы электрическое поле бегущего по спиральной структуре импульса.
Собственно, сила трения, направленная против ускоряющей силы, равна коэффициенту трения, умноженному на радиальную силу, прижимающую макрочастицу к внутренней поверхности канала. В свою очередь, эта радиальная сила пропорциональна силе ускорения и отклонению макрочастицы от оси, в силу азимутальной симметрии системы, радиальная сила отсутствует, когда центр макрочастицы находится на оси системы.
Пусть отклонение макрочастицы от оси системы составляет 1% от ее радиуса, dout/2=1 cm, то есть Δr=100 µ. Из разложения функции Бесселя первого порядка при малом аргументе, следует, что пара сил, действующая на диполь, при этом будет равна:
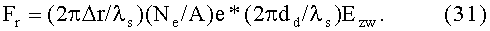
Типичное значение коэффициента трения, например целлофана по целлофану, [5], стр.128, равно: kfr=0.4. С одной стороны, коэффициент трения скольжения возрастает, если трущиеся поверхности находятся в вакууме, с другой стороны, он падает с увеличением скорости относительного движения поверхностей. Будем считать, что при наших скоростях движения макрочастицы внутри канала коэффициент трения имеет примерно такое же значение. Тогда отношение силы, направленной против скорости, Ff, к силе ускорения равно:
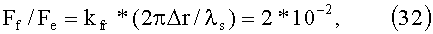
что будет компенсироваться автофазировкой.
Найдем упругую силу Felas, которая будет препятствовать сжатию макрочастицы из закона Гука:
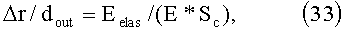
где Δr/dout=5*10-3 - относительное сжатие, Е - модуль Юнга, Sc - площадь контакта.
Длину хорды а при высоте сегмента Δr можно найти из формулы:
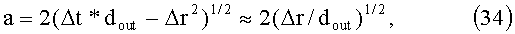
и тогда площадь контакта равна: Sc=dd*a=3*10-5 m2. Типичное значение модуля Юнга Е для пластмасс равно Е=108 N/m2, [3], стр.53 и из формулы (33) получим, что значение силы Felas равно: Felas=15N, что сравнимо с радиальной силой Fr, которую надо умножить на число нуклонов А=1.13*1025, Fr=5*10-3*5.2*10-4*1.6*10-19*1.13*1025=5N.
Видно, что значительному радиальному смещению центра тяжести макрочастицы относительно оси системы будет препятствовать сила упругости, возвращающая центр тяжести макрочастицы на ось системы.
Выводы
Эффективность ускорения заряженных макрочастиц цилиндрической формы уменьшается с ростом диаметра цилиндра. Это связано с тем, что электрический заряд располагается на поверхности цилиндра, площадь единичного отрезка цилиндра растет как радиус, а объем и масса растут как квадрат радиуса. В результате заряд, приходящийся на единицу массы (нуклон) с ростом радиуса, уменьшается как 1/r и начиная с некоторого радиуса темп ускорения макрочастицы - электрического диполя, градиентом поля волны, становится больше темпа ускорения заряженной макрочастицы.
Выбор макрочастицы в форме плоского конденсатора - электрического диполя - позволяет избежать этого падения темпа ускорения, что позволяет набирать макрочастице скорость порядкам первой космической на длине менее одного километра.
Литература
1. С.Н.Доля. Способ ускорения магнитных диполей, Патент РФ, №2451894.
2. С.Н.Доля. Способ ускорения макрочастиц, Патент РФ, №2456782.
3. Таблицы физических величин. Справочник под ред. И.К.Кикоина, Москва, Атомиздат, 1976.
4.http://ru.wikipedia.org/wiki/Титанат_бария стронция.
5. Физические величины. Справочник под ред. И.С.Григорьева и Е.З.Мейлихова. Москва, Энергоатомиздат, 1991.
6. С.Н.Доля, К.А.Решетникова, Об электродинамическом ускорении макроскопических частиц, Сообщение ОИЯИ, Р9-2009-110, Дубна, 2009, http://arxiv.org/ftp/arxiv/papers/0908/0908.0795.pdf.
7. И.М.Капчинский. Динамика частиц в линейных резонансных ускорителях, Москва, Атомиздат, 1966.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ УСКОРЕНИЯ МАКРОЧАСТИЦ | 2012 |
|
RU2510603C2 |
| СПОСОБ УСКОРЕНИЯ МАГНИТНЫХ ДИПОЛЕЙ | 2011 |
|
RU2451894C1 |
| СПОСОБ УСКОРЕНИЯ МАГНИТНЫХ ДИПОЛЕЙ | 2010 |
|
RU2442941C1 |
| СПОСОБ УСКОРЕНИЯ МАГНИТНЫХ ДИПОЛЕЙ | 2012 |
|
RU2510164C2 |
| СПОСОБ УСКОРЕНИЯ МАКРОЧАСТИЦ | 2010 |
|
RU2456782C2 |
| СПОСОБ ЭЛЕКТРОСТАТИЧЕСКОГО УСКОРЕНИЯ МАКРОЧАСТИЦ | 2011 |
|
RU2455800C1 |
| СПОСОБ УСКОРЕНИЯ ТЕЛА | 2014 |
|
RU2558509C1 |
| СПОСОБ СОЗДАНИЯ НАПРАВЛЕННОГО ВЗРЫВА | 2012 |
|
RU2498199C1 |
| КОМПЛЕКС АППАРАТУРЫ ДЛЯ ВОЗДУШНОГО НАБЛЮДЕНИЯ | 2013 |
|
RU2535381C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ПОДВОДНЫХ ОБЪЕКТОВ | 2012 |
|
RU2495448C1 |
Изобретение относится к области ускорительной техники и может быть использовано для решения научных и прикладных задач. Ускорение макрочастиц в данном способе осуществляют градиентом поля бегущего по спиральной структуре электрического импульса. Способ ускорения макрочастиц заключается в том, что их предварительно электрически заряжают, предварительно ускоряют газодинамическим способом до скорости, соответствующей скорости инжекции в спиральный волновод, и окончательно ускоряют полем бегущего по виткам спирального волновода импульса напряжения. В качестве макрочастиц используют плоский конденсатор, который ускоряют полем бегущего по виткам импульса напряжения, при этом ускорение плоского конденсатора ведут в диэлектрическом канале, предотвращая его разворот на 180 градусов и его отклонение от оси ускорения. Технический результат - увеличение темпа ускорения. 1 ил., 1 табл.
Способ ускорения макрочастиц, заключающийся в том, что их предварительно электрически заряжают, предварительно ускоряют газодинамическим способом до скорости, соответствующей скорости инжекции в спиральный волновод, и окончательно ускоряют полем бегущего по виткам спирального волновода импульса напряжения, отличающийся тем, что в качестве макрочастиц используют плоский конденсатор, который ускоряют полем бегущего по виткам импульса напряжения с темпом ускорения ΔW/Δz=(Ne/A)e*(2πdd/λs)*Ezw0*sinφs, где ΔW/Δz - набор энергии плоским конденсатором на единице длины, eNe/A - электрический заряд какого-либо знака, расположенный на плоском конденсаторе и приходящийся на один нуклон в нем, dd - расстояние между обкладками плоского конденсатора, λs - длина волны ускорения в спиральном волноводе, Ezw0 - амплитуда волны, φs - синхронная фаза, при этом ускорение плоского конденсатора ведут в диэлектрическом канале, предотвращая его разворот на 180 градусов и его отклонение от оси ускорения.
| СПОСОБ УСКОРЕНИЯ МАКРОЧАСТИЦ | 2010 |
|
RU2456782C2 |
| СПОСОБ УСКОРЕНИЯ МАГНИТНЫХ ДИПОЛЕЙ | 2011 |
|
RU2451894C1 |
| EP 1617713A1, 18.01.2006 | |||
| US 2011101892A1, 05.05.2011 | |||
Авторы
Даты
2014-07-20—Публикация
2013-03-19—Подача