Изобретение относится к спектрометрии корпускулярных излучений, преимущественно к исследованию энергетических спектров космических частиц на ИСЗ и космических аппаратах.
Известны электростатические спектрометры для измерения дифференциальных энергетических спектров, содержащие электростатические анализаторы, в которых применяется отклоняющий конденсатор с неплоскими пластинами, чаще всего с пластинами сферической [1] или цилиндрической [2] формы. Однако расширение диапазона исследуемых энергий в сторону их увеличения усложняет реализацию анализаторов подобного типа, так как требует прецизионного изготовления криволинейных поверхностей с большим радиусом кривизны.
Известен также дифференциальный электростатический спектрометр типа плоского электронного зеркала [3], в котором анализируемые частицы вводятся в зазор плоского конденсатора через отверстие в одной из пластин под углом θ к пластине, а выводятся через другое отверстие в той же пластине после отклонения частиц в электрическом поле конденсатора. Однако при высоких энергиях эффективный размер входного окна в таком спектрометре становится весьма малым и чувствительность спектрометра мала.
Наиболее близким к заявляемому изобретению представляется устройство с двумя плоскими конденсаторами, состыкованными под некоторым углом (далее - шевронный анализатор). Схема расположения электродов опубликована в [4]. Однако в [4] решена лишь математическая задача об электрическом поле в зазоре такого шевронного конденсатора с полубесконечными пластинами. Приведенное в [4] шевронное расположение является необходимым, но еще не достаточным условием построения дифференциального анализатора. Очевидно также, что анализатор с полубесконечными пластинами неработоспособен.
Целью изобретения является увеличение отношения сигнал/шум путем указания ограничений на геометрические и электрические параметры такого анализатора, достаточные для обеспечения его работы в нужном дифференциальном режиме.
Цель достигается тем, что угол шеврона выбирается равным 180о - 2 β, где угол β находится в пределах  ≅ tgβ ≅
≅ tgβ ≅  , где 2d - величина зазора между пластинами конденсатора; L - длина пластины (фиг. 1).
, где 2d - величина зазора между пластинами конденсатора; L - длина пластины (фиг. 1).
Целью изобретения является также повышение чувствительности анализатора.
Анализатор (фиг. 1) содержит пару плоских конденсаторов с обкладками 1, 2 и 3, 4, источник 5 питания и детектор 6. Исследуемые частицы попадают внутрь конденсатора (1, 2) через его торец 7. На фиг. 2-6 показаны траектории частиц, соответствующие минимальной T1 и максимальной T2 энергиям частиц, проходящих через анализатор и попадающих на детектор. На фиг. 2 показаны также система координат и величины, используемые ниже при вычислении граничных энергий T1 и T2.
Анализатор работает следующим образом. Заряженная частица влетает в зазор анализатора в точке yo (фиг. 2) под углом α , определяемым из соотношения tgα = 

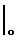 = y
= y , и далее движется в электрическом поле Е по траектории, описываемой уравнением
, и далее движется в электрическом поле Е по траектории, описываемой уравнением
y = _  x2+y
x2+y x+yo (1) где K =
x+yo (1) где K =  , qe - заряд частицы; T∞ - кинетическая энергия частицы в свободном от поля пространстве.
, qe - заряд частицы; T∞ - кинетическая энергия частицы в свободном от поля пространстве.
Минимальной энергии T1 соответствует K1 и в первом конденсаторе траектория с yo= = -d (d - полуширина зазора между пластинами), yk = d (yk - значение y в точке касания xk), yk' = 0, yL' = -tgβ (yL' - значение y' при выходе из зазора первого конденсатора). Во втором конденсаторе траектория с T1 симметрична траектории в первом конденсаторе относительно вертикали на фиг. 2. Для отыскания K1, xk, yo', yL воспользуемся уравнением траектории (1) для x = L.
yL= -  L2+y
L2+y L-d а также продифференцированным по x уравнением (1) в точке x = xk
L-d а также продифференцированным по x уравнением (1) в точке x = xk
-tgβ = - 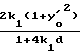 L+y
L+y Напишем также соответствующие уравнения для x = xk
Напишем также соответствующие уравнения для x = xk
d = - 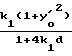 x
x xk-d
xk-d
0 = - 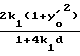 xk+y
xk+y Из этих уравнений находим связь между K1, tg β и геометрией конденсатора λ =
Из этих уравнений находим связь между K1, tg β и геометрией конденсатора λ = 
k1 =  Подставив в эту формулу K1=
Подставив в эту формулу K1= 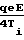 ,E =
,E =  =
=  , где U - разность потенциалов между пластинами конденсатора, а также выразив tg α в единицах λ , т.е. положив tgα=γλ , получим окончательно для T1
, где U - разность потенциалов между пластинами конденсатора, а также выразив tg α в единицах λ , т.е. положив tgα=γλ , получим окончательно для T1
T1 = qeU  (2) При λ<<1
(2) При λ<<1
T1≈ qeU  Зависимость
Зависимость  от λ,γ показана на фиг. 7.
от λ,γ показана на фиг. 7.
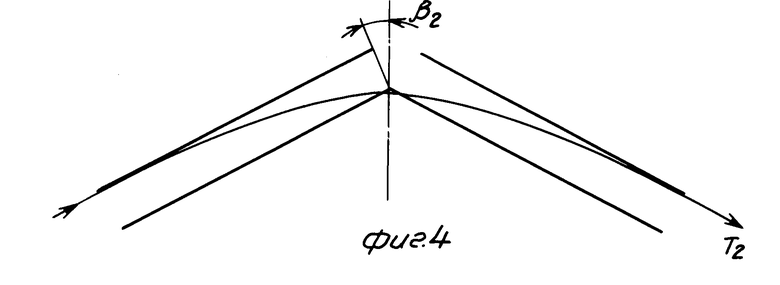
Максимальной энергии T2 соответствует K2. При угле β1 , отвечающем соотношению tgβ = 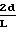 =λ (т.е. γ = 1), анализатор оптически непрозрачен, его пропускание частиц с энергией T2=∞ становится нулевым (фиг. 3), при дальнейшем увеличении β анализатор становится дифференциальным, т.е. пропускает только частицы с энергиями, находящимися между T1 и T2.
=λ (т.е. γ = 1), анализатор оптически непрозрачен, его пропускание частиц с энергией T2=∞ становится нулевым (фиг. 3), при дальнейшем увеличении β анализатор становится дифференциальным, т.е. пропускает только частицы с энергиями, находящимися между T1 и T2.
Зависимость T2 (λ,γ) в интервале углов β между β1 и β2 , показанными на фиг. 3 и 4, находится с использованием условий на входе и выходе yo = d, yL = -d, yL' = -tg β . Для уравнения траектории (1) в этом интервале имеем
-d = - 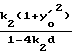 L2+y
L2+y L+d Дифференцируя по x в точке x = L, имеем также
L+d Дифференцируя по x в точке x = L, имеем также
-tgβ = - 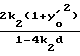 L + y
L + y Зависимость T2 (λ,γ), полученная из этих уравнений, имеет вид
Зависимость T2 (λ,γ), полученная из этих уравнений, имеет вид
T2= qeU 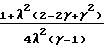 (3) При λ<<1
(3) При λ<<1
T2= qeU  При β=β2 (фиг. 4) условия на входе и выходе имеют вид yo = d, yo' = 0, yL = -d, yL' = - tg β2, а T2= qeU
При β=β2 (фиг. 4) условия на входе и выходе имеют вид yo = d, yo' = 0, yL = -d, yL' = - tg β2, а T2= qeU  и tg β2 = 2 λ , т. е. γ = 2.
и tg β2 = 2 λ , т. е. γ = 2.
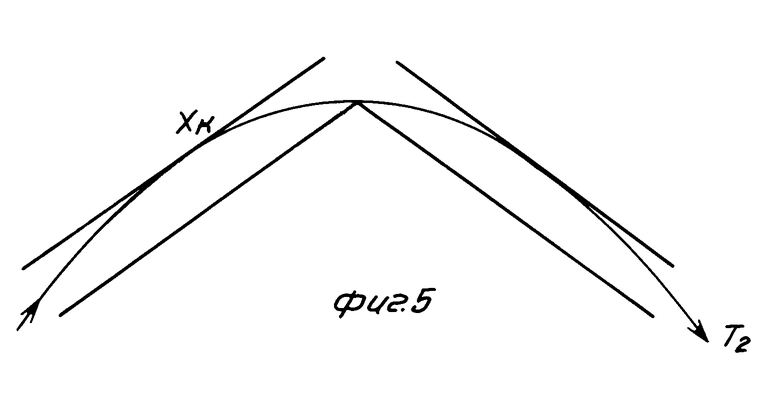
В интервале углов β между β2 и β3 (фиг. 4 - 6) траектории частиц с T2 определяются величинами yk = d, yk' = 0, yL= = -d, yL' = -tg β . Соответствующая пара уравнений для части траектории (фиг. 5), начинающейся в xk, будет иметь вид
-d = -  (L-xk)2+d
(L-xk)2+d
-tgβ = - 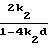 (L-xk) Полученная из этих уравнений зависимость T2 (λ, γ) выражается как
(L-xk) Полученная из этих уравнений зависимость T2 (λ, γ) выражается как
T2= qeU 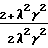 (4) При λ<<1
(4) При λ<<1
T2≈ qeU 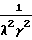 При β = β2, когда γ= 2, (4) совпадает с (2). Оба участка (3) и (4) показаны на фиг. 7.
При β = β2, когда γ= 2, (4) совпадает с (2). Оба участка (3) и (4) показаны на фиг. 7.
Предельный угол β=β3 анализатора соответствует случаю, когда T1 = T2, т. е. случаю, когда анализатор "запирается" и перестает пропускать частицы. Уголβ3 определяется соотношением tgβ3=4λ , т.е. γ = 4. Значение T2 = T1 при β3 равно qeU 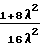 .
.
Таким образом, предлагаемое устройство в виде двух одинаковых простых плоских конденсаторов, расположенных в форме шеврона (фиг. 1), без каких-либо дополнительных коллиматоров на входе, снабженное только источником питания и детектором частиц, образует дифференциальный электростатический спектрометр с границами пропускания по энергии T1 и T2 в интервале углов β , определяемом соотношением λ≅tgβ≅4λ.
Шевронный электростатический анализатор такого спектрометра позволяет продвинуться в область высоких энергий без изменения формы пластин конденсаторов или U путем лишь изменения угла шеврона и расстояния между пластинами; позволяет изменять ширину полосы пропускания T2-T1 при данном λ путем изменения β ; прост по конструкции и в изготовлении, так как имеет плоские обкладки отклоняющих конденсаторов и не требует специального коллиматора на входе; входным окном служит торец первого конденсатора.
Наличие двух одинаковых конденсаторов не является необходимым условием конструкции предлагаемого устройства. Анализатор в виде расположенных под углом 180о - 2 β двух конденсаторов с разными λ1 и λ2 также работоспособен, но значения T1 и T2 для такого анализатора будут отличаться от приведенных на фиг. 7.
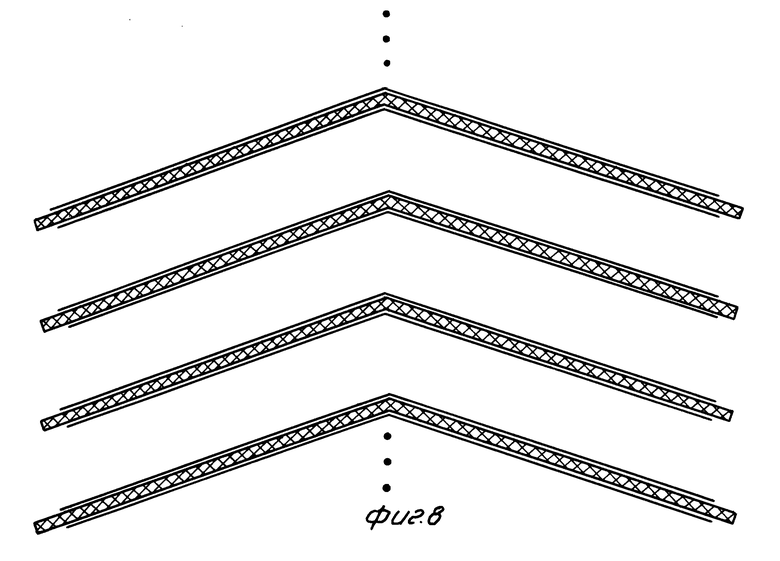
Для работы в области высоких энергий предлагаемый одиночный шевронный анализатор будет иметь малую величину λ , если на его продольный габарит наложены ограничения, а следовательно, малую площадь входного зазора и малую чувствительность. Однако шевронная геометрия, в отличие от сферической или цилиндрической, позволяет увеличить чувствительность в n раз путем объединения n одинаковых пар рассмотренных конденсаторов в пакет (фиг. 8). Обкладками соседних пар служат в таком пакете изолированные один от другого проводящие слои, нанесенные на противоположные стороны пластин из изоляционного материала.
В качестве примера рассмотрим характеристики шевронного анализатора с T2 = =1,2 МэВ; U = 20 кВ; γ = 3. Значение λ для диапазона γ 2...4 находится по формуле (4)
λ2= 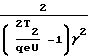 =
= 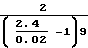 = 1.87·10-3
= 1.87·10-3
λ = 4.32·10-2
tgβ=3λ=0,1296; β=7o25' Значение T1 находится по формуле (2)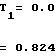 2
2 = 0.02
= 0.02  = ΔT = T2-T1 = 1,2-0,824 = 0,376 МэВ. Средняя энергия To = (T1+T2)/2 = 1,042 МэВ. ΔT/To= = 0,376/1,042 = 0,361 = 36,1%. ( ΔT/To)1/2 = =18%, что вполне приемлемо для измерений в космическом пространстве. В случае же цилиндрического конденсатора с 2d = Δr= 1 см для энергии To≃ 1 МэВ при U = =20 кВ потребовались бы отклоняющие пластины с радиусами кривизны ~
= ΔT = T2-T1 = 1,2-0,824 = 0,376 МэВ. Средняя энергия To = (T1+T2)/2 = 1,042 МэВ. ΔT/To= = 0,376/1,042 = 0,361 = 36,1%. ( ΔT/To)1/2 = =18%, что вполне приемлемо для измерений в космическом пространстве. В случае же цилиндрического конденсатора с 2d = Δr= 1 см для энергии To≃ 1 МэВ при U = =20 кВ потребовались бы отклоняющие пластины с радиусами кривизны ~  Δr =
Δr =  · 1 = 100 см = 1 м. Многослойный шевронный анализатор может быть изготовлен, например, из фольгированного стеклотекстолита.
· 1 = 100 см = 1 м. Многослойный шевронный анализатор может быть изготовлен, например, из фольгированного стеклотекстолита.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ обнаружения подводного источника широкополосного шума | 2019 |
|
RU2715431C1 |
| ВРЕМЯПРОЛЕТНЫЙ МАСС-АНАЛИЗАТОР | 2023 |
|
RU2841356C1 |
| СПОСОБ АНАЛИЗА ЗАРЯЖЕННЫХ ЧАСТИЦ ПО МАССАМ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2431214C1 |
| СПОСОБ ПОСТРОЕНИЯ ИНТЕГРАЛЬНОЙ ЗОНЫ ПОРАЖЕНИЯ ГРУППИРОВКИ ОГНЕВЫХ СРЕДСТВ | 2010 |
|
RU2430384C1 |
| ЭЛЕКТРОСТАТИЧЕСКИЙ СПЕКТРОМЕТР ДЛЯ ЭНЕРГЕТИЧЕСКОГО И УГЛОВОГО АНАЛИЗА ЗАРЯЖЕННЫХ ЧАСТИЦ | 1988 |
|
SU1814427A1 |
| Массэнергоанализатор | 1985 |
|
SU1290431A1 |
| АХРОМАТИЧЕСКИЙ ЭЛЕКТРОСТАТИЧЕСКИЙСПЕКТРОМЕТР С ПОПЕРЕЧНЫМ ОТКЛОНЯЮЩИМЭЛЕКТРИЧЕСКИМ ПОЛЕМ | 1971 |
|
SU425244A1 |
| МАГНИТНЫЙ МАСС-СПЕКТРОМЕТР С ДВОЙНОЙ ФОКУСИРОВКОЙ | 2000 |
|
RU2176836C2 |
| Масс-спектрометр | 1980 |
|
SU993362A1 |
| Ионный микрозондовый анализатор | 1988 |
|
SU1605288A1 |





Использование: относится к спектрометрии корпускулярных излучений, преимущественно к исследованию энергетических спектров на космических аппаратах. Анализатор образован двумя плоскими конденсаторами. За ними расположен детектор. Повышение его чувствительности достигается путем указания ограничений на его геометрические параметры и выполнения его в виде пакета из одинаковых анализаторов. 1 з.п. ф-лы, 8 ил.
 ≅ tgβ ≅
≅ tgβ ≅  ,
,
где 2d - величина зазора между пластинами конденсатора, м;
L - длина пластины.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Коган В.И., Назаров А.Г., Хабибуллаев П.К | |||
| Журнал технической физики, 1987, т.57, N 6, с.1150. | |||
Авторы
Даты
1994-10-30—Публикация
1990-09-20—Подача