Изобретение относится к испытаниям и может использоваться при исследовании работоспособности объектов (радиоэлектронной аппаратуры, узлов, блоков, комплектующих изделий и т.п.), функционирующих в условиях комплексного воздействия внешних и других факторов.
Известны способы испытаний [1], предусматривающие определение показателей стойкости (надежности) исследуемых объектов путем воспроизведения на экспериментальных установках уровней факторов (механических климатических и др.), имеющих место в реальных условиях эксплуатации.
Недостатком таких испытаний является их малая информативность, поскольку результаты получаются на уровне да-нет, т.е. выдержал или не выдержал объект данный режим испытаний.
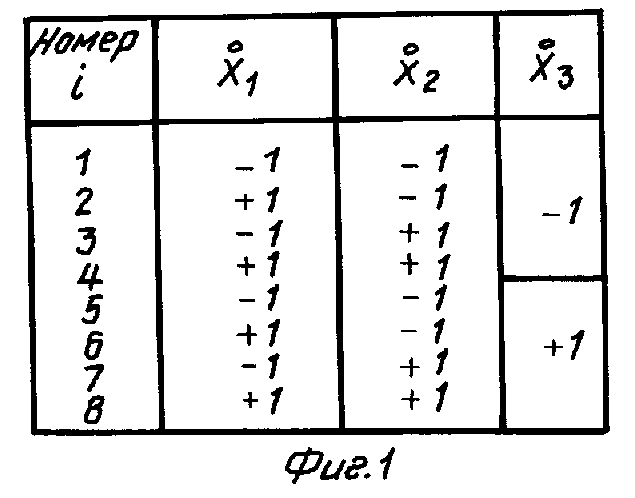
Известны активные многофакторные испытания объекта [2], проводимые по специальным планам - полного факторного эксперимента (ПФЭ), ортогональным и ротатабельным центральным композиционным планам (соответственно ОЦКП и РЦКП) и др. Примерный вид плана ПФЭ, ОЦКП и РЦКП представлен на фиг. 1-3 соответственно для трехфакторного случая. Для удобства воздействующие факторы представлены в центрированном виде: =
=  , l =
, l =  , i =
, i =  (1) где xli и
(1) где xli и  - соответственно реальное и центрированное значение l-го фактора, воспроизводимые на экспериментальной установке для i-го сочетания;
- соответственно реальное и центрированное значение l-го фактора, воспроизводимые на экспериментальной установке для i-го сочетания;
хlмакс и хlмин - соответственно максимальное и минимальное значения этого же фактора;
m - число учитываемых факторов;
N - число их сочетаний, воспроизводимых в ходе испытаний.
В ходе таких испытаний уровни воздействующих факторов задаются на экспериментальных установках в соответствии с планами (ПФЭ, ОЦКП, РЦКП) и измеряются значения параметров исследуемого объекта. По полученным данным - матрице х воздействующих факторов (размерностью N строк и m столбцов) и матрице y выходных параметров (размерностью N строк и n столбцов, где n - число учитываемых параметров объекта) строятся математические модели реакции параметров объекта на воздействие факторов:
yj=f(x1, x2, . . . , xm, Aj), j = 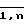 ,(2) где yj - j-й выходной параметр объекта;
,(2) где yj - j-й выходной параметр объекта;
хl - l-й воздействующий фактор ((l =  ));
));
Аj= [a1, a2,...,am] - вектор коэффициентов модели (2);
М - число коэффициентов модели (2) - размер вектора Аj.
Численные значения коэффициентов регрессии аl (компонентов вектора Aj) определяются расчетным путем из условия минимума дисперсии Dj (суммы квадратов разностей между экспериментальными и расчетными значениями j-го выходного параметра объекта);
Dj = 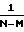
 (y
(y ));
));
хl - значение l-го воздействующего фактора ((l = 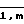 )) для i-го сочетания, устанавливаемого согласно плану испытаний (см., например, фиг. 1-3).
)) для i-го сочетания, устанавливаемого согласно плану испытаний (см., например, фиг. 1-3).
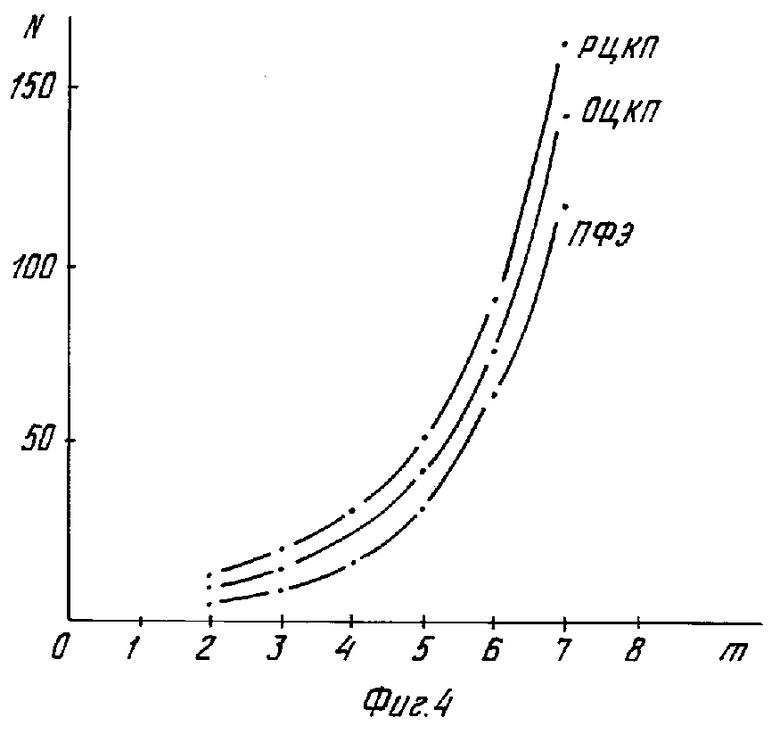
Тем не менее такие испытания, обеспечивая получение достаточно информативных моделей (2) для исследования объектов, обладают недостатками, в частности требуют фиксированного и достаточно большого числа испытаний (фиг. 4) для построения моделей (2), что увеличивает продолжительность и стоимость испытаний, часто не позволяют полностью воспроизвести план активных испытаний на реальных экспериментальных установках, что снижает адекватность моделей (2).
Целью изобретения является повышение эффективности испытаний за счет построения адекватной модели (2) при меньшем объеме испытаний (меньшем числе N).
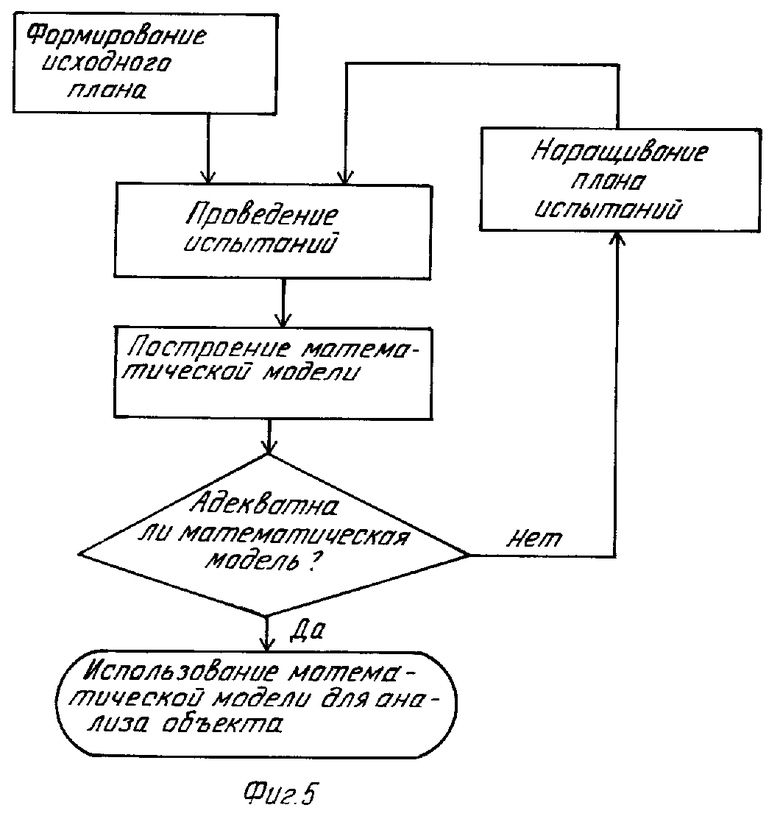
Для достижения цели поступают следующим образом (см. фиг. 5). Формируют исходный план, содержащий минимально необходимое число испытаний No, при котором уже становится возможным получать модель (2), из условия No > m+1, для чего используют, например, часть плана ПФЭ (фиг. 1), отобрав из него No строк. Проводят испытания по этому плану, устанавливая соответственно уровни воздействующих факторов и измеряя значения выходных параметров объекта благодаря чему формируются исходные матрицы х и y, содержащие по No строк. Задают вид модели (2), например, в виде уравнения регрессии (если вид модели неизвестен заранее):
f(x1,..., xm, Aj) = a1+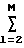 alZl (4) где zl - l-й условный фактор, представляющий собой как какой-либо воздействующий фактор и/или его функциональное преобразование (например, zl=x12), так и/или взаимосочетания факторов (например, zl=x1x2).
alZl (4) где zl - l-й условный фактор, представляющий собой как какой-либо воздействующий фактор и/или его функциональное преобразование (например, zl=x12), так и/или взаимосочетания факторов (например, zl=x1x2).
Определяют искомые численные значения коэффициентов Аjматематической модели (2), для чего решают систему из М уравнений относительно Аj: f(y
f(y = 0, l =
= 0, l =  (5)
(5)
Оценивают адекватность моделей (2), используя, например, критерий Фишера, для чего вычисляют величину
Fj = 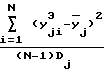 , j =
, j =  (6) где
(6) где =
= 
 y
y
Величину Fj при степенях свободы ν1 = N-1 и ν2 = N-M сравнивают с табличными значениями Fтабл (4). Если Fj > Fтабл, то считают,что модель (2) адекватна с соответствующей доверительной вероятностью, ее можно использовать для решения задач моделирования поведения объекта и испытания на этом прекращают. В противном случае (модель неадекватна) испытания продолжают. Продолжение испытаний заключается в том, что наращивается матрица х (увеличивается число N) путем определения значений факторов по выражению
хli = xlмин + ζ (хlмакс-хlмин), l =  , (7) где ζ - величина, лежащая в пределах от 0 до 1 и определяемая из условия минимальной корреляции между факторами, для чего могут быть использованы, например, таблицы случайных чисел (4).
, (7) где ζ - величина, лежащая в пределах от 0 до 1 и определяемая из условия минимальной корреляции между факторами, для чего могут быть использованы, например, таблицы случайных чисел (4).
Центрирования полученных по выражению (7) величин хli по формуле (1), занесения их в матрицу Х дополнительной строкой и воспроизведения полученного сочетания факторов на экспериментальных установках с последующим замером выходных параметров объекта и занесением их соответствующей строкой в матрицу y.
Уточняется (или оставляется неизменным) вид модели (2), по полученным матрицам х и y через выражение (5) вычисляются коэффициенты вектора Аj, вновь оценивается адекватность модели (2), например, по критерию Фишера и принимается решение о прекращении испытаний и использовании полученной модели (2) или о продолжении испытаний.
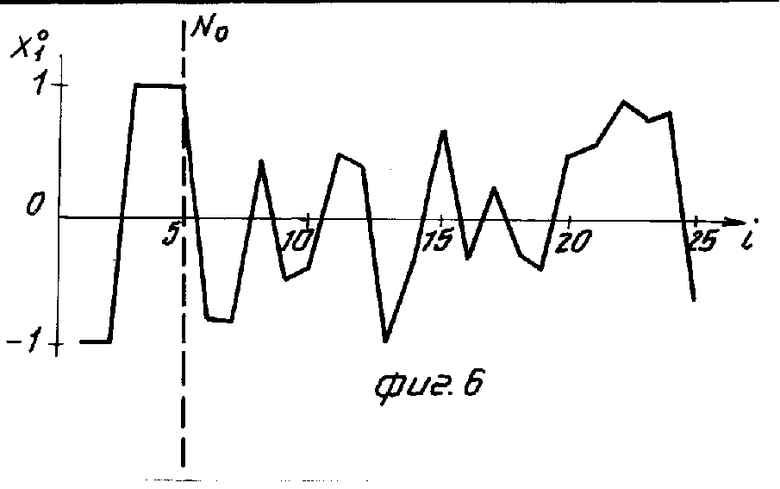
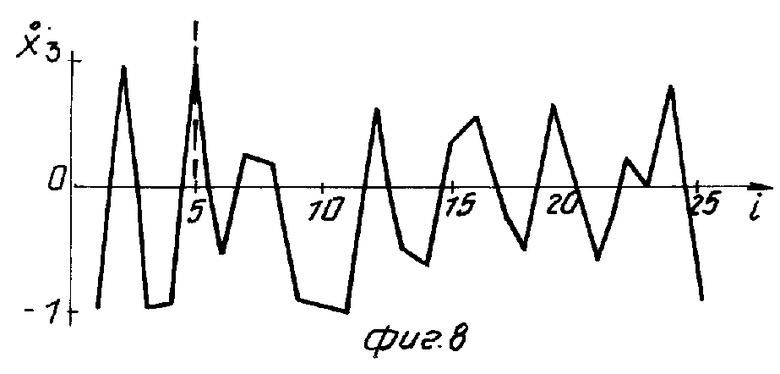
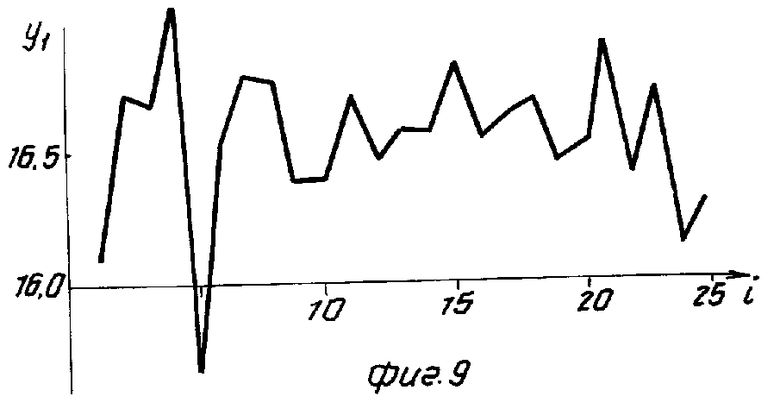
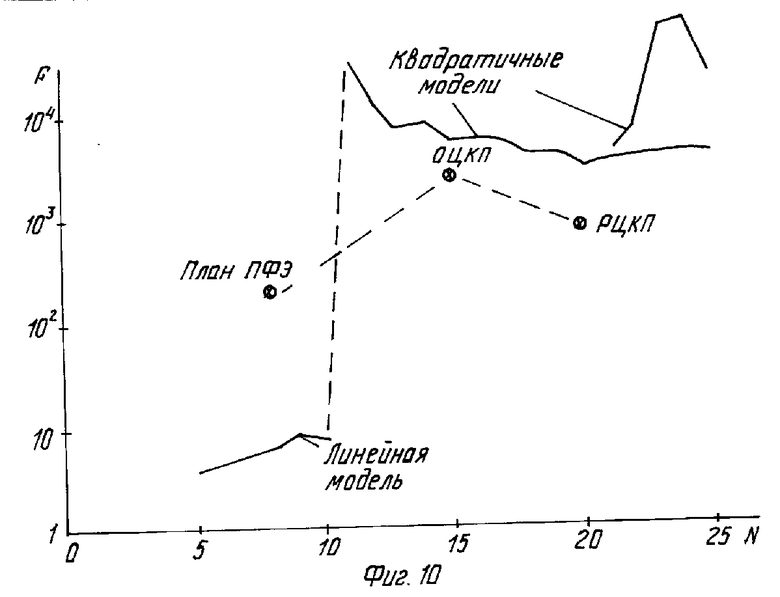
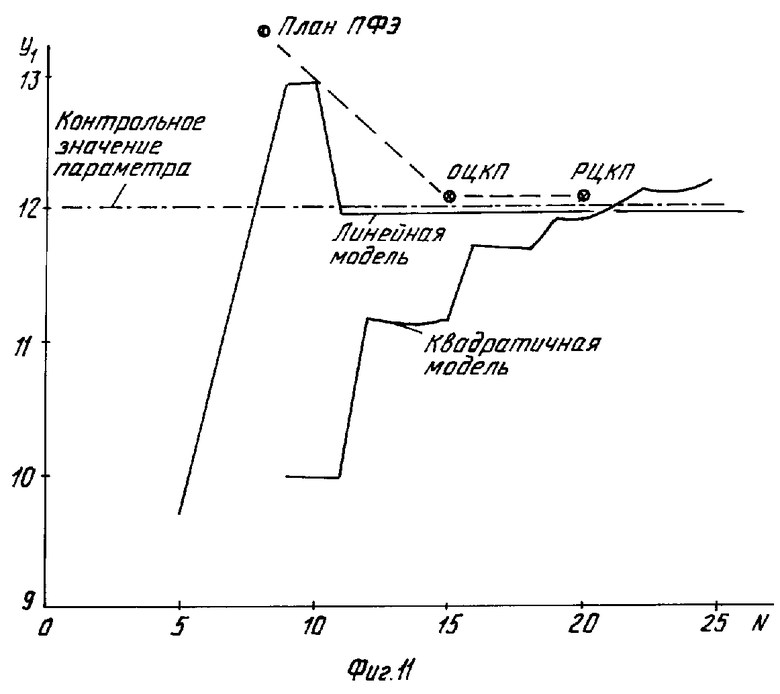
На фиг. 4 показана зависимость числа испытаний N для различных планов активных испытаний от числа m учитываемых факторов; на фиг. 5 - схема проведения испытаний и анализа их результатов; на фиг. 6-8 - изменение центрированных уровней воздействующих факторов (температуры, атмосферного давления и коэффициента нагрузки) в ходе испытаний реле заявляемым способом; на фиг. 9 - соответствующее изменение выходного параметра объекта (реле) - напряжения срабатывания; на фиг. 10 - сопоставительные уровни адекватности (величины критериев Фишера) моделей (2,4) при испытаниях по плану ПФЭ, ОЦКП, РЦКП и при планировании в соответствии с заявляемым способом; на фиг. 11 - проверка точности полученных модулей путем сопоставления с контрольным значением выходного параметра.
Заявляемый способ проиллюстрирован на примере испытаний реле (5). В рамках данного подхода оно было представлено в виде объекта, имеющего один (n=1) выходной параметр - напряжение срабатывания y1 и подверженного воздействию трех (m=3) факторов - температуры окружающего воздуха (х1), атмосферного давления (х2) и коэффициента нагрузки (х3). Требуется провести испытания реле на воздействие указанных факторов с целью построения математической модели (2):
y1= f (x1, x2, x3, A1) (8) и последующего ее использования для оценки работоспособности реле и решения других практических задач. Поскольку вид модели (2, 8) заранее не известен ввиду сложности протекающих процессов, ищут ее в виде уравнения регрессии (4).
Формируют исходный план, для чего случайным образом выбираю из плана ПФЭ (фиг. 1) пять (No=5) строк и, задавая соответствующим образом комплексы температуры (х1), давления (х2) и коэффициента нагрузки (х3), измеряют значения напряжения срабатывания (y1) и формируют матрицы х и y (матрица y имеет один столбец). Уравнение регрессии (4) ищут сначала в линейном виде:
y1= A1тZт, (9) где Z=[1, x1, x2, x3] - вектор условных факторов, а численные значения коэффициентов регрессии (вектора А1) получают из решения системы (5) из четырех (М=4) уравнений, что может быть осуществлено любым известным способом, например (3).
Оценка адекватности модели (9) по критерию Фишера (вычисление величины F1 по формуле (6) и сопоставление с табличным значением (4), а также пересчет контрольной точки для  = 2,
= 2,  = 2 и
= 2 и  = 2показали в целом удовлетворительные результаты (см. фиг. 10, 11). Тем не менее испытания были продолжены (скорее с исследовательской целью) причем каждое новое значение факторов выбиралось случайным образом из диапазона между их минимальным и максимальным значениями по формуле (7) (см. фиг. 6-8).
= 2показали в целом удовлетворительные результаты (см. фиг. 10, 11). Тем не менее испытания были продолжены (скорее с исследовательской целью) причем каждое новое значение факторов выбиралось случайным образом из диапазона между их минимальным и максимальным значениями по формуле (7) (см. фиг. 6-8).
В результате испытаний были получены еще более точные модели (9), среди которых полная и неполная квадратичные (векторы Z для них равны соответственно [1, x1, x2, x3, x1x2, x1x3, x2x3] и [1, x1,x2,x3, x1x2, x1x3, x2x3, x12x22, x32]). Эти модели и были эффективно использованы для решения следующих задач: прогнозирования напряжения срабатывания реле в различных эксплуатационных режимах, компенсации нежелательного воздействия неуправляемых факторов за счет управляемого изменения других факторов (например, стабилизация напряжения срабатывания реле при колебаниях коэффициента нагрузки и пониженного атмосферного давления за счет управления температурным режимом), такого подбора эксплуатационного режима (факторов х1, х2, х3), когда напряжение срабатывания y1 было бы экстремальным, определения допустимых рабочих областей для реле на множестве факторов {x1, x2, x3} и т. п.
Для подтверждения эффективности заявляемого способа были проведены испытания этого же реле классическим образом (по плану ПФЭ, ОЦКП и РЦКП), что также позволило получить адекватные модели (9) (см. фиг. 10,11).
Тем не менее по сравнению с классическими активными испытаниями заявляемый способ является более эффективным - модель (2, 4, 9), пригодную для анализа параметров объекта, становится возможным получить по относительно малому числу испытаний, например, в случае реле (5)-11 испытаний вместо 20 по плану РЦКП или 15 по ОЦКП. Кроме того, заявляемый способ испытаний обходится без "звездных плеч", характерных для ОЦКП и РЦКП, в ряде случаев превышающих возможности испытательного оборудования.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ КОМБИНИРОВАННОГО ИСПЫТАНИЯ ОБЪЕКТОВ | 1992 |
|
RU2025708C1 |
| СПОСОБ КОМБИНИРОВАННЫХ ИСПЫТАНИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1991 |
|
RU2007699C1 |
| Стенд для комплексных испытаний объектов | 1990 |
|
SU1711009A1 |
| Стенд для комплексных испытаний объектов | 1988 |
|
SU1675714A1 |
| УСТРОЙСТВО ИНДИКАЦИИ ВЗЯТИЯ ВОРОТ В ФУТБОЛЕ | 1991 |
|
RU2008055C1 |
| УСТРОЙСТВО ИНДИКАЦИИ ПОЛОЖЕНИЯ "ВНЕ ИГРЫ" В ФУТБОЛЕ | 1992 |
|
RU2028814C1 |
| УСТРОЙСТВО ДЛЯ УКРЫТИЯ ФУТБОЛЬНОГО ПОЛЯ | 1991 |
|
RU2016605C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ПОЛУПРОВОДНИКОВОГО ТЕНЗОРЕЗИСТОРНОГО ПРЕОБРАЗОВАТЕЛЯ ДАВЛЕНИЯ | 1994 |
|
RU2097720C1 |
| ВЕРТОЛЕТ | 1992 |
|
RU2009078C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ ПОСЛЕОПЕРАЦИОННОГО РЕЦИДИВА МНОГОУЗЛОВОГО ЗОБА С ПОМОЩЬЮ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ | 2009 |
|
RU2398289C1 |



Изобретение относится к испытаниям объектов (блоков радиоэлектронной аппаратуры, деталей, узлов и т. п.) на комплексное воздействие внешних и других факторов и направлено на повышение эффективности испытаний за счет построения адекватной математической модели реакции параметров объекта на воздействие факторов при меньшем объеме испытаний. Сущность способа заключается в том, что строится исходный план испытаний объекта (на основе, например, известного плана полного факторного эксперимента) и проводятся испытания в соответствии с этим планом, по результатам испытаний строится математическая модель и оценивается ее адекватность если адекватность удовлетворительная, то испытания прекращают и используют полученную модель в практических целях, если адекватность недостаточная, то наращивают план испытаний, вводят в него комбинации факторов, исходя из минимальной коррекции между уровнями факторов в общем плане, проводят испытания в соответствии с вновь определенной комбинацией факторов, вновь переходят к построению математической модели и т.д. При использовании предложенного способа испытаний для построения адекватной модели требуется значительно меньший объем испытаний, а уровни факторов соответствует возможностям испытательного оборудования. 11 ил.
СПОСОБ КОМПЛЕКСНЫХ ИСПЫТАНИЙ, включающий в себя выбор исходных факторов, определение исходных уровней 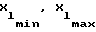 минимального и максимального уровней i-го фактора, испытание объекта, измерение значений выходных параметров, построение математической модели вида Jj = f(X1, X2,..., Xm, Aj),
минимального и максимального уровней i-го фактора, испытание объекта, измерение значений выходных параметров, построение математической модели вида Jj = f(X1, X2,..., Xm, Aj),  где Jj j-й выходной параметр объекта, Xl - l-й воздействующий фактор
где Jj j-й выходной параметр объекта, Xl - l-й воздействующий фактор  Aj = (a1, a2,...,am) - вектор коэффициентов математической модели, и оценка ее адекватности, отличающийся тем, что выбирают число испытаний Nо в зависимости от количества факторов m, где No > m + 1, если адекватность модели удовлетворительна, испытания прекращают и используют полученную модель, а если ее адекватность недостаточна, то испытания продолжают, при продолжении испытаний добавляют дополнительную комбинацию факторов, уровни
Aj = (a1, a2,...,am) - вектор коэффициентов математической модели, и оценка ее адекватности, отличающийся тем, что выбирают число испытаний Nо в зависимости от количества факторов m, где No > m + 1, если адекватность модели удовлетворительна, испытания прекращают и используют полученную модель, а если ее адекватность недостаточна, то испытания продолжают, при продолжении испытаний добавляют дополнительную комбинацию факторов, уровни 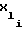 которых определяют из выражения
которых определяют из выражения
где ζ∈[0,1] - случайная величина, выбираемая по равномерному закону распределения,
затем измеряют выходные параметры объекта, строят математическую модель и вновь оценивают ее адекватность, если адекватность полученной модели удовлетворительна, то испытания прекращают и используют полученную модель, а если адекватность недостаточна, то испытания и выбор новых уровней проводят до получения адекватной модели.
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Статистические методы в инженерных исследованиях | |||
| Лабораторный практикум./Под ред.Г.К.Круга | |||
| М.: Высшая школа, с.38-42, 100-106. | |||
Авторы
Даты
1995-01-20—Публикация
1992-04-01—Подача