Изобретение относится к измерительной технике, а именно к способам определения соотношения фаз, в частности к способам определения квадратурных фазовых сдвигов между синусоидальными сигналами одинаковой частоты, и предназначено для преимущественного использования в устройствах, работающих на инфранизких частотах, когда амплитуды сигналов могут значительно различаться между собой и изменяться в широких пределах.
Известны различные способы определения квадратурных фазовых сдвигов между двумя синусоидальными сигналами при измерении их разности фаз [1, 2, 3] Эти способы характеризуются сложностью из-за большого количества операций формирования дополнительных импульсов в определенные моменты времени, сравнения временных интервалов, введения коэффициентов модуляции, корреляции и т. п. В таких способах возникают дополнительные погрешности определения квадратурных фазовых сдвигов при малой амплитуде хотя бы одного из сигналов, особенно в инфранизкочастотной области измерений. Эти погрешности обусловлены уменьшением скорости изменения сигналов, что ведет к неоднозначности моментов времени срабатывания пороговых устройств.
Известны более простые осциллографические способы определения соотношений фаз с помощью фигур Лиссажу, когда по фигуре в виде эллипса на экране осциллографа определяют квадратурные фазовые сдвиги между синусоидальными сигналами.
В способе [4] исследуемые сигналы подают каждый на свою пару отклоняющих пластин. При этом определение квадратурных фазовых сдвигов между сигналами затруднено из-за конечной разрешающей способности осциллографа, определяемой шириной луча, к тому же при малом значении амплитуды хотя бы одного из сигналов регистрация исследуемых напряжений будет осуществляться на нелинейном участке отклоняющего напряжения. Кроме того, погрешность регистрации исследуемых сигналов с помощью осциллографа возрастает в инфранизкочастотном диапазоне из-за трудностей количественных оценок измерений.
Известен другой способ [5] в соответствии с которым исследуемые сигналы перемножают и получают напряжение, имеющее переменную составляющую и постоянную составляющую. Квадратурный фазовый сдвиг между сигналами определяют, когда постоянная составляющая становится равной нулю.
Недостатки способа заключаются в том, что значения переменной составляющей, так же как и постоянной составляющей, зависят от величин исследуемых сигналов. Поэтому при изменении исследуемых сигналов в больших пределах изменяются в большом диапазоне и составляющие полученного сигнала после перемножения, что затрудняет обеспечение высокой точности при выделении постоянной составляющей, особенно на инфранизких частотах.
Наиболее близким техническим решением к заявляемому по общим используемым признакам является способ определения соотношения фаз двух синусоидальных сигналов [6] основанный на анализе результата взаимодействия сигналов, в соответствии с которым величины одного исследуемого сигнала делят на величины другого, регистрируют сигнал-частное, выбирают по крайней мере два значения сигнала-частного на временном интервале, расположенном в пределах половины любого периода сигнала-делителя и не превышающем по длительности этот полупериод, таким образом, чтобы в пределах этого интервала два выбранных значения сигнала-частного различались между собой по величине больше возможной погрешности сравнения этих значений, и определяют соотношение фаз сигналов делимого и делителя по характеру изменения значений сигнала-частного на интервале полупериода сигнала-делителя.
Способ весьма эффективен при изменении сигналов в большом динамическом диапазоне, а также на инфранизких частотах, однако способ не позволяет определять квадратурные фазовые сдвиги между исследуемыми синусоидальными сигналами.
Целью изобретения является расширение функциональных возможностей при измерениях.
Цель в способе определения квадратурных фазовых сдвигов синусоидальных сигналов, основанном на анализе результата взаимодействия исследуемых сигналов на выбранном интервале времени, в соответствии с которым величины одного исследуемого сигнала делят на величины другого, регистрируют сигнал-частное, достигается тем, что значения сигнала-частного ограничивают по величине и усредняют на выбранном интервале времени, а квадратурный фазовый сдвиг между исследуемыми сигналами определяют, когда полученное усредненное значение будет равно нулю; интервал времени для усреднения выбирают таким образом, чтобы его середина совпадала с серединой одной из полуволн сигнала-делителя.
Сущность изобретения заключается в том, что, совершив простейшее действие над исследуемыми сигналами деление величин их друг на друга однозначно определяют квадратурные фазовые сдвиги по равенству нулю усредненного на выбранном интервале времени значения регистрируемого сигнала-частного.
При делении двух синусоидальных сигналов одной частоты сигнал-частное представляет собой функцию времени:
f (t)=[Asin (ω t+F1)]/[Bsin( ω t+F2)] (1) где K=A/B, Bsin( ω t+F2)≠0; F1 и F2 фазы двух исследуемых сигналов; А и В измеряемые амплитуды исследуемых колебаний. Функция f(t) будет периодической прерывной функцией и по виду напоминать функции тангенсов или котангенсов.
В случае F1>F2, F2=0 выражение (1) запишем аналогично с [6] следующим образом для K> 0, 0< Fo< π/2 и К< 0, π/2< Fo< π
f (t)= K[cosFo+sinFoctg(2 πt/T)] (2) где Т=2 π/ω Fo разность фаз между исследуемыми сигналами.
В случае F2>F1, F1=0 можно записать для К>0, π/2<Fo<0 и К<0, π < Fo < -π/2:
f(t)=K{1/[cosFo+sinFo ctg(2 πt/T)] (3)
Положив Fo= -270 или Fo=90 (первый вариант квадратурных фазовых сдвигов между двумя синусоидальными сигналами), будем иметь следующие значения: sinFo= 0; cosFo= 1. Подставляя эти значения в выражения (2) и (3), получим соответственно:
f (t)=K[ctg(2 πt/T)] (4)
f(t)=K[tg(2 πt/T)] (5)
Положив Fo=270 или Fo=-90 (второй возможный вариант квадратурных фазовых сдвигов между двумя синусоидальными сигналами), будем иметь следующие значения: sinFo=-1,cosFo=0. Подставляя их в выражения (2) и (3), получим соответственно:
f (t)=-K[ctg(2 πt/T)] (6)
f (t)=-K[tg(2 πt/T)] (7)
Следовательно, в случае квадратурных фазовых сдвигов получим функцию f(t) в виде функции тангенса или котангенса, умноженных на соответствующие коэффициенты К, то есть будем иметь функцию f(t), симметричную относительно момента времени t(0), соответствующего середине рассматриваемого полупериода сигнала-делителя (фиг. 1, 2). Коэффициент К будет определять лишь наклон функции f(t). Следовательно, на интервалах времени внутри любого рассматриваемого полупериода сигнала-делителя, середины которых совпадают, площади фигур, ограниченные осью абсцисс и функцией f(t) сигнала-частного, равны между собой (фиг. 1, 2).
Среднее значение fc функции f(t) определяется через интеграл следующим образом:
fс= (1/T)  f(t) dt (8) где Т интервал усреднения.
f(t) dt (8) где Т интервал усреднения.
Так как в рассматриваемом интервале времени площади над осью абсцисс и под осью абсцисс равны, а середина этого интервала совпадает с серединой полуволны сигнала-делителя, то среднее значение fc на этом интервале времени равно нулю:
fс= (2/T) f(t) dt - (2/T)
f(t) dt - (2/T)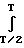 f(t) dt 0
f(t) dt 0
Таким образом, усредненное значение функции f(t) сигнала-частного для квадратурных фазовых сдвигов двух синусоидальных сигналов равно нулю, причем усреднять значения можно на большом интервале времени или на сравнительно малом интервале времени, середина которого совпадает с серединой полуволны рассматриваемого сигнала-делителя. При использовании интервала времени для усреднения, который гораздо больше, чем интервал времени, соответствующий полупериоду исследуемых сигналов, можно считать, что условие соответствия середин интервалов времени всегда выполняется.
При изменении амплитуд исследуемых сигналов при сохранении их соотношений значения функции f(t) не будут изменяться, что также повышает точность измерений при анализе фазовых соотношений.
При малых отклонениях от квадратурных фазовых сдвигов двух синусоидальных сигналов значения функции f(t) cигнала-частного будут подниматься или опускаться относительно оси абсцисс, то есть будет нарушаться симметрия функции f(t) относительно середины рассматриваемого полупериода сигнала-делителя, следовательно, будут различаться и площади фигур над осью абсцисс и под осью абсцисс. Поэтому при усреднении значений функции f(t) в тех же условиях будет наблюдаться постоянная составляющая, знак которой будет зависеть от величины отклонения фазового сдвига от квадратурного.
Для повышения разрешающей способности следует симметрично ограничивать по уровню сигнал-частное, что уменьшает величину сравниваемых площадей. В этом случае при нарушенивии симметрии функции f(t) можно получить увеличение чувствительности (фиг. 1, 2).
Устройство для реализации предлагаемого способа представлено на фиг. 3. Оно содержит блок 1 деления и блок регистрации осциллограф 2, первый вход которого подключен к выходу блока 1 деления, на два входа последнего подают синусоидальные сигналы Х(t) и Y(t), причем первое сигнал-делимое, второе сигнал-делитель, который также подключен к второму входу осциллографа 2. В качестве блока деления был использован цифровой вольтметр В7-23, работающий в режиме деления, и выбран двухлучевой осциллограф типа С1-83. Блок деления можно выполнить аналогично [7]
Устройство работает следующим образом. Входные сигналы напряжений Ux(t) и Uy(t) поступают на первый и второй входы блока 1 деления. Сигнал-делитель напряжением Uy(t) поступает также на второй вход осциллографа 2. На выходе блока 1 деления получают напряжение U1(t), пропорциональное частному от деления двух сигналов Ux(t)/Uy(t), изменяющееся на интервале полупериода сигнала-делителя по закону, близкому к виду функции тангенса или котангенса. Если сигнал-делимое Ux(t), к примеру, опережает сигнал-делитель Uy(t), то U1(t) имеет вид котангенса. Это напряжение U1(t) поступает на первый вход двухлучевого осциллографа 2. По экрану осциллографа сравнивают площади фигур над осью абсцисс и под осью абсцисс, ограниченные функцией сигнала-частного напряжения U1(t). Временной интервал выбирают относительно середины полуволны сигнала-делителя. При равенстве площадей анализируемых фигур определяют квадратурный фазовый сдвиг между исследуемыми сигналами.
Предлагаемый способ не только позволяет определять квадратурный фазовый сдвиг между синусоидальными сигналами по сравнению с прототипом, но также имеет существенные преимущества перед другими рассмотренными способами по простоте и точности, особенно в инфранизкочастотном диапазоне даже тогда, когда амплитуды исследуемых колебаний значительно различаются между собой, изменяясь при этом в большом динамическом диапазоне.



Применение: изобретение относится к измерительной технике,а именно к способам определения квадратурных фазовых сдвигов двух синусоидальных сигналов. Сущность изобретения: после деления величин исследуемых сигналов друг на друга получают сигнал - частное, значения которого ограничивают и усредняют на выбранном интервале времени, а квадратурный фазовый сдвиг между сигналами определяют, когда усредненное значение будет равно нулю. 1 з.п. ф-лы, 3 ил.
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| Алексенко А.Г., Коломбет Е.А., Стародуб Г.И | |||
| Применение прецизионных аналоговых ИС | |||
| М.: Советское радио, 1980, с.100-102. | |||
Авторы
Даты
1995-05-20—Публикация
1993-08-05—Подача