Изобретение относится к области спектрального анализа сигналов и предназначено для определения действующего значения гармонических составляющих в сигнале, также может использоваться для оценки нелинейности четырехполюсника, когда требуется обеспечить быстродействие и точность измерений.
Известен способ спектрального анализа, в соответствии с которым для определения действующего значения высших гармоник в каждом канале сигнал непосредственно фильтруют в узкой полосе частот, детектируют и интегрируют (или возводят в квадрат, детектируют и усредняют) [1.а, б]
Такому способу присущи недостатки громоздкость фильтров не инфранизких частотах, большая погрешность от неравномерности АЧХ фильтров, малое быстродействие.
Известен другой способ спектрального анализа сигнала [2] основанный на преобразовании частоты исследуемого сигнала и выделении спектральных составляющих и огибающих амплитуд.
Такой способ имеет также низкое быстродействие и погрешности от использования фильтров на низких частотах.
Известен способ безгетеродинного спектрального анализа [3] заключающийся в сжатии сигналов во времени с переменным коэффициентом преобразования временного масштаба, который определяет дискретизацию выборки сигнала, и используемый для узкополосной фильтрации выборки постоянной длительности сжатого во времени сигнала при всех значениях коэффициента преобразования времени масштаба.
Недостатки способа на инфранизких частотах аналогичные погрешности АЧХ фильтров и низкое быстродействие.
Наиболее близким способом по общим используемым признакам, взятым за прототип, является способ [4] гармонического анализа сигнала известной частоты, основанный на преобразовании входного сигнала и измерении результата на индикаторе, в соответствии с которым выделяют временные интервалы, определяемые экстремумами входного сигнала, измеряют длительность интервалов между экстремумами, сравнивают ее с заданным интервалом, находят разность указанных длительностей и по ее величине судят об относительном содержании высших гармонических составляющих в сигнале.
Способ можно использовать на инфранизких частотах, он имеет высокое быстродействие, довольно прост, однако имеет низкую точность, так как работает только при больших искажениях во входном сигнале, кроме этого нельзя определять действующее значение высших гармоник в сигнале.
Целью изобретения является повышение точности измерений при расширении функциональных возможностей.
Цель в способе определения действующего значения гармонических составляющих в сигнале, основанном на преобразовании входного сигнала, в соответствии с которым выделяют определенные временные интервалы для анализа, достигается тем, что определяют действующее значение входного сигнала, определяют частоту первой гармоники входного сигнала, формируют опорный синусоидальный сигнал с частотой первой гармоники входного сигнала, выбирают первый временной интервал, в котором входной сигнал не изменяет свой знак, определяют середину первого временного интервала, выбирают второй временной интервал, в котором опорный синусоидальный сигнал не изменяет свой знак, определяют середину второго временного интервала, измеряют мгновенные значения входного сигнала в момент времени t1, а опорного сигнала в момент времени t2, причем моменты времени t1 и t2 выбирают равноотстоящими соответственно от середины первого и второго временных интервалов, определяют модуль отношения мгновенных значений входного и опорного сигналов, многократно определяют модули отношения мгновенных значений входного и опорного сигналов для каждой пары моментов времени, равноотстоящих от середин соответственно первого и второго временных интервалов, определяют усредненное значение модулей отношения мгновенных значений входного и опорного сигналов, а действующее значение гармонических составляющих входного сигнала определяют как корень квадратный из разности квадратов двух величин действующего значения входного сигнала и произведения действующего значения опорного синусоидального сигнала на усредненное значение модулей отношения мгновенных значений входного и опорного сигналов.
Сущность способа заключается в том, что действующее значение Ue гармонических составляющих во входном сигнале определяют при помощи математического выражения:
где Uд действующее значение входного сигнала;
Uод действующее значение опорного синусоидального сигнала;
Kс усредненное значение модулей отношения мгновенных значений входного и опорного сигналов, для определения которого формируют опорный синусоидальный сигнал с частотой первой гармоники входного сигнала, многократно определяют модули отношения мгновенных значений входного и опорного сигналов для каждой пары моментов времени, равноотстоящих от середин выбранных временных интервалов, внутри которых, соответственно, входной и опорный сигналы не изменяют свои знаки.
Входной квазисинусоидальный сигнал Ux(t) и опорный синусоидальный сигнал Uy(t) с частотой "ω" (первой гармоники) представим в виде отдельных функций, рассматриваемых на выбранных временных интервалах bj, не содержащих сигналов, равных нулю:
Ux(t)=Ux(bj), (1)
Uy(t)=Uy(bj), (2)
где t время;
Ux(bj), Uy(bj) соответствующие сигналы на выбранных временных интервалах bj.
Сигналы Ux(bj) и Uy(bj) на выбранных временных интервалах bj будем аппроксимировать в виде фрагментов синусоид, для которых
где Ax, Ay значения амплитуд аппроксимирующих сигналов;
ω значения круговой частоты сигналов;
Fx, Fy начальные фазы входного и опорного сигналов.
Разделим мгновенные значения входного и опорного сигналов друг на друга и рассмотрим функцию f(bj):
f(bj)=Ka[sin(ωt+Fx)]/sin(ωt+Fy), (5)
где f(bj) функция на интервале времени bj, определяемая отношением двух сигналов Ux(bj) и Uy(bj);
Ka=(Ax/Ay) отношение амплитуд сигналов из (3) и (4).
Для момента времени t0 на интервале bj, когда значение функции f(bj)= f(t0)=Ka, должно выполняться условие:
[sin(ωto+Fx)]/[sin(ωt+Fy)]=1 (6)
Обозначим левую часть уравнения (6) через L, тогда:
Разность фаз F0 между сигналами Ux(bj) и Uy(bj) равна:
F0=Fx-Fy, (8)
Если, к примеру, Fx>Fy, то можно принять Fy=0, и после преобразования из выражения (7) получим:
L=cosFo+(sinFo)/(tgωt) (9)
Если Fx<Fy, то можно принять Fx=0, и после преобразования из выражения (7) получим:
L=1/[cosFo+(sinFoctgωt)] (10)
Выполнение условия (6) сводится к выполнению условия:
cosFo+sinFo/[tg(2π/T)to]=1, (11)
где t0 соответствует искомому моменту времени;
T период первой гармоники входного сигнала.
Обозначим (2π/T)to=β значение угла, определяемого положением t0 на интервале времени периода T. Тогда после перестановок выражение (11) перепишем в следующем виде:
tgβ=sinFo/(1-cosFo). (12)
После преобразований получим:
sinF0/(1-cosF0) ctg(F0/2) (13)
Из (12 и 13) следует:
tgβ=ctg(Fo/2). (14)
Из выражения (14) получим:
tgβ=tg[(π/2)-(Fo/2)] (15)
После преобразования получим:
tgβ=tg[(π-Fo)/2] (16)
Из равенства (16) получаем выражение для β:
b=(π-Fo)/2 . (17)
Так как β=(2π/T) t0 соответствует моменту времени, когда выполняется условие (6), то из (17) определим положение точки t0 на интервале bj. Угол π соответствует полупериоду, то есть такому интервалу времени, когда значение входного или опорного сигнала имеет один и тот же знак. Положение точки t0 на интервале bj соответствует середине интервала времени, лежащего внутри одного из полупериодов, из которого исключен интервал времени, соответствующий сдвигу фаз между сигналами. Этот момент времени t0 находится на одинаковом расстоянии от середин выбранных интервалов времени, где не происходит изменение знака входного или опорного сигнала, см. фиг.1.
Значения синусоидальных сигналов в момент времени t0 на середине интервала, равного фазовому сдвигу F0, будут равны соответственно Axsin(F0/2) и Aysin(F0/2), а отношение мгновенных значений сигналов будет определяться как Ka=Ax/Ay.
Измерение мгновенного значения входного сигнала можно проводить в момент времени t1, отстоящий от середины выбранного первого временного интервала этого сигнала, к примеру, на интервал времени, соответствующий фазовому сдвигу F0 или [(π/2) F0] а измерение опорного сигнала в момент времени t2, отстоящий от середины выбранного второго временного интервала своего сигнала на интервал времени соответственно F0 или [ (π/2) F0] Для момента времени t1 мгновенное значение входного сигнала можно представить, как AxsinF0= Axcos[(π/2) F0] а мгновенное значение опорного сигнала в момент времени t2 можно представить, как AysinF0=Aycos[(π/2) F0] Модуль отношения мгновенных значений входного и опорного синусоидальных сигналов будет равен Ka=Ax/Ay.
Мгновенное значение одного сигнала в момент времени  будет равно AxcosF0, другого сигнала в момент времени
будет равно AxcosF0, другого сигнала в момент времени  будет равно AycosF0. Модуль их отношений будет равен Ka Ax/Ay.
будет равно AycosF0. Модуль их отношений будет равен Ka Ax/Ay.
Следовательно, если измерять отношения мгновенных значений сигналов синусоидальной формы в различные моменты времени, равноотстоящие от середин выбранных временных интервалов полуволн своих сигналов, то модули K(ωt) отношений мгновенных значений входного и опорного сигналов будут равны K(ωt) Ka=Ax/Ay.
Если во входном сигнале будут искажения, обусловленные присутствием гармонических составляющих входного сигнала, то будут наблюдаться отклонения в получаемых значениях модулей отношения мгновенных значений входного и опорного сигналов.
На фиг.1 показан пример определений моментов времени t0, t1, t2, равноотстоящих от середин выбранных временных интервалов-полуволн входного и опорного сигналов, для произвольного фазового сдвига между сигналами. Для фазового сдвига F0 получают несколько пар моментов времени t1; t2; 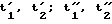 и так далее. AxsinF0/AysinF0= Ka для измерений в моменты времени t1 и t2; AxcosF0/AycosF0 для измерений в моменты времени
и так далее. AxsinF0/AysinF0= Ka для измерений в моменты времени t1 и t2; AxcosF0/AycosF0 для измерений в моменты времени 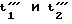 и так далее.
и так далее.
Измерения в момент времени t0 можно рассматривать как частный случай выбора соответствующей пары, когда t1=t2.
Действующее значение Ue гармонических составляющих Ui(t) во входном сигнале U(t) можно определить из соотношений [6]
где U(t) представляет из себя функцию входного сигнала без составляющей первой гармоники входного сигнала.
Запишем входной сигнал напряжения U(t) в виде:
U(t)=βsinωt+g(t) (19)
где β амплитуда синусоидального напряжения первой гармоники входного сигнала;
g(t) некоторая функция, значения которой изменяются во времени так, чтобы выполнялось равенство (19).
Предположим, что опорный синусоидальный сигнал U(y)=U'(t) имеет частоту w первой гармоники, тогда:
U′(t)=Aosin(ωt+Fo) (20)
где A0 амплитуда опорного синусоидального сигнала;
F0 сдвиги фаз между входным и опорным сигналами.
Для каждого из фазовых сдвигов F0 будем определять модули K(ωt) отношения мгновенных значений входного U(t1) и опорного U'(t2) сигналов. Тогда входной сигнал U(t) можно представить в виде:
U(t)=[Aosin(ωt)]K(ωt) (21)
где K(ωt) текущие значения модулей отношения мгновенных значений входного U(t) и опорного U'(t) сигналов, вычисленных для различных пар моментов времени t1 и t2, равноотстоящих от середин соответственно первого и второго выбранных временных интервалов. При этом можно записать:
Если входной сигнал синусоида, то есть g(t)=0 в (19), то при различных фазовых сдвигах при усреднении значений модулей K(ωt) отношения мгновенных значений входного и опорного сигналов получают одно и то же значение Kc, которое численно будет равно Kc β /A0, и тогда входной сигнал U(t) представим в виде:
U(t)=(AoKc)sin(ωt)+g(t) (23)
Из (21) и (23) определим выражение для функции g(t):
где K0 усредненное значение модулей отношения мгновенных значений входного и опорного сигналов.
Подставляя (25) в (19), получим для входного сигнала:
U(t)=AoKcsin(ωt)+Aosin(ωt)[K(ωt)-Kc] (26)
Из (26) можно определить значение квадрата входного сигнала:
Из [6] получим выражение для квадрата действующего значения входного сигнала в следующем виде:

После преобразования выражение (29) будет иметь вид:
Из (30) среднеквадратическое значение входного сигнала можно представить в следующем виде:
Первое слагаемое правой части выражения (31) представляет собой квадрат произведения действующего значения опорного синусоидального сигнала на усредненное значение Kc модулей отношения мгновенных значений входного и опорного сигналов, что соответствует составляющей первой гармоники входного сигнала, поэтому (31) можно записать в следующем виде:
где Uoд действующее значение опорного синусоидального напряжения;
K(ωt) -текущие значения модулей отношения мгновенных значений входного и опорного сигналов;
Kс усредненное значение модулей отношения мгновенных значений входного и опорного сигналов.
Разность квадратов двух величин K(ωt) и Kc в выражении (32) можно представить в виде квадрата корня квадратного из разности квадратов этих же величин, поэтому (32) можно представить в следующем виде: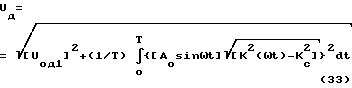
Первое слагаемое под общим корнем в правой части выражения (33) представляет собой квадрат действующего значения составляющей первой гармоники входного сигнала, а второе слагаемое равно квадрату действующего значения гармонических составляющих входного сигнала.
Следовательно, выражение (33) можно представить в следующем виде:
Из (34) получим окончательное выражение для действующего значения гармонических составляющих Ue входного сигнала:
Таким образом, действующее значение гармонических составляющих входного сигнала равно корню квадратному из разности квадратов двух величин - действующего значения входного сигнала и произведения действующего значения опорного синусоидального сигнала на усредненное значение Kc модулей отношения K(ωt) мгновенных значений входного и опорного сигналов.
Следует отметить, что в предлагаемом способе не требуется отдельно выделять ни первую гармонику, ни высшие гармоники, что повышает быстродействие, а повышение точности достигается особенно в тех случаях, когда действующее значение входного сигнала уже известно или когда измерить действующее значение сигнала не представляет труда при использовании стандартной аппаратуры.
На фиг.2 приведена структурная схема устройства, реализующего способ.
Устройство содержит формирователь 1, управляемый опорный генератор 2, фазовращатель 3, блок индикации 4, блок 5 для измерения действующего значения входного сигнала. Блоки в устройстве соединены следующим образом. Формирователь 1, управляемый опорный генератор 2 и фазовращатель 3 соединены последовательно. Вход устройства соединен с входом блока 5 для измерения действующего значения входного сигнала, с входом формирователя 1 и с первым входом блока 4 индикации, второй вход которого подключен к выходу фазовращателя 3.
Устройство работает следующим образом. Входной сигнал Ux(t) поступает на блок 5 для измерения действующего значения входного сигнала, на первый вход блока 4 индикации и на вход формирователя 1, на выходе которого формируется напряжение U1, пропорциональное периоду T первой гармоники входного сигнала. Это напряжение U1 поступает на вход управляемого опорного генератора 2, на выходе которого получают напряжение U2 синусоидальной формы, период которых зависит от управляемого напряжения U1 и равен периоду T первой гармоники входного сигнала.
Синусоидальное напряжение U2 амплитудой Ay с выхода опорного генератора 2 поступает на вход фазовращателя 3, на выходе которого получают синусоидальное напряжение Uy(t) той же амплитуды, которая не изменяется при изменениях фазовых сдвигов. Для синусоидального напряжения амплитудой Ay известно его действующее значение, которое равно  Ay. Таким образом, на два входа блока индикации двухлучевого осциллографа 4 поступают входные сигналы Ux(t) и опорные синусоидальные сигналы напряжения Uy(t), имеющие между собой фазовой сдвиг, к примеру, как показано на фиг.1. Для каждого фазового сдвига F0 производят измерения мгновенных значений входного Ux(t1) и опорного Uy(t2) сигналов, определяют модули K(ωt) отношения мгновенных значений при выбранной паре моментов времени t1 и t2 соответственно, каждый из которых равноотстоит от середины выбранных временных интервалов, внутри которых входной и опорный сигналы соответственно не изменяют своих знаков. Эти временные интервалы соответствуют полуволнам входного и опорного сигналов. Вычисленные значения модулей K(ωt) усредняют и получают значения Kc.
Ay. Таким образом, на два входа блока индикации двухлучевого осциллографа 4 поступают входные сигналы Ux(t) и опорные синусоидальные сигналы напряжения Uy(t), имеющие между собой фазовой сдвиг, к примеру, как показано на фиг.1. Для каждого фазового сдвига F0 производят измерения мгновенных значений входного Ux(t1) и опорного Uy(t2) сигналов, определяют модули K(ωt) отношения мгновенных значений при выбранной паре моментов времени t1 и t2 соответственно, каждый из которых равноотстоит от середины выбранных временных интервалов, внутри которых входной и опорный сигналы соответственно не изменяют своих знаков. Эти временные интервалы соответствуют полуволнам входного и опорного сигналов. Вычисленные значения модулей K(ωt) усредняют и получают значения Kc.
Действующее значение гармонических составляющих входного сигнала определяют как корень квадратный из разности квадратов двух величин - действующего значения U5 на выходе блока 5 и произведения действующего значения  Ay опорного синусоидального сигнала Uy(t) на усредненное значение Kc модулей Kωt отношения мгновенных значений входного и опорного синусоидального сигналов.
Ay опорного синусоидального сигнала Uy(t) на усредненное значение Kc модулей Kωt отношения мгновенных значений входного и опорного синусоидального сигналов.
Для повышения разрешающей способности следует уменьшать величину фазового сдвига, увеличивая количество этих фазовых сдвигов. При использовании прецизионного опорного генератора способ имеет высокую разрешающую способность, способ не требует использования узкополосных фильтров, что существенно повышает быстродействие и точность.
Используемые источники информации
1. Мирский Г.Я. Аппаратурное определение характеристик случайных процессов. М. Энергия, 1972, а) с.234, б) с. 247.
2. Калинчук Б.А. Пиастро В.П. Анализаторы инфранизких случайных процессов. М. Энергия, 1973, с.116.
3. Авторское свидетельство СССР N 1287034, кл.G01R 23/16, 1987.
4. Авт. свид. СССР N 1113751, кл.G01R, 23/16, 1984 (прототип).
5. Измерения в электронике. Справочник. М. Энергоатом, 1987, с.382 -383.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ КОЭФФИЦИЕНТА НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ СИГНАЛА | 1993 |
|
RU2090900C1 |
| СПОСОБ ИЗМЕРЕНИЯ СРЕДНЕКВАДРАТИЧЕСКОГО ЗНАЧЕНИЯ СИГНАЛА | 1993 |
|
RU2090895C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛОВ | 1993 |
|
RU2090898C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛА | 1993 |
|
RU2065168C1 |
| СПОСОБ ГАРМОНИЧЕСКОГО АНАЛИЗА СИГНАЛА ДЛЯ ОЦЕНКИ МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ | 1993 |
|
RU2075756C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ АБСОЛЮТНОГО СРЕДНЕГО СИГНАЛА | 1993 |
|
RU2065169C1 |
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА СИГНАЛА | 1994 |
|
RU2086991C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА НЕЛИНЕЙНЫХ ИСКАЖЕНИЙ | 1993 |
|
RU2065170C1 |
| СПОСОБ ГАРМОНИЧЕСКОГО АНАЛИЗА СИГНАЛА | 1992 |
|
RU2010246C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ОТНОШЕНИЯ ЗНАЧЕНИЙ АМПЛИТУД КВАЗИСИНУСОИДАЛЬНЫХ СИГНАЛОВ | 1994 |
|
RU2093886C1 |

Изобретение относится к измерительной технике и предназначено для измерения действующего значения гармонических составляющих в сигнале, может использоваться для оценки нелинейности четырехполюсника, когда требуется обеспечить быстродействие и точность измерений. Способ спектрального анализа сигнала основан на преобразовании входного сигнала, в соответствии с которым выделяют определенные временные интервалы, при этом определяют действующее значение входного сигнала, определяют частоту первой гармоники входного сигнала, формируют опорный синусоидальный сигнал с частотой первой гармоники входного сигнала, выбирают первый временной интервал, в котором входной сигнал не изменяет свой знак, определяют середину первого временного интервала, выбирают второй временной интервал, в котором опорный синусоидальный сигнал не изменяет свой знак, определяют середину второго временного интервала, измеряют мгновенные значения входного сигнала в момент времени t1, а опорного сигнала - в момент времени t2, причем моменты времени t1 и t2 выбирают равноотстоящими соответственно от середины первого и второго временных интервалов, определяют модуль отношения мгновенных значений входного и опорного сигналов, многократно определяют модули отношения мгновенных значений входного и опорного сигналов для каждой пары моментов времени, равноотстоящих от середин соответственно первого и второго временных интервалов, определяют усредненное значение модулей мгновенных значений входного и опорного сигналов, а действующее значение гармонических составляющих входного сигнала определяют как корень квадратный из разности квадратов двух величин - действующего значения входного сигнала и произведения действующего значения опорного синусоидального сигнала на усредненное значение модулей отношения мгновенных значений входного и опорного сигналов.
Способ определения действующего значения гармонических составляющих в сигнале, основанный на преобразовании входного сигнала, в соответствии с которым выделяют определенные временные интервалы для анализа, отличающийся тем, что определяют действующее значение входного сигнала, определяют частоту первой гармоники входного сигнала, формируют опорный синусоидальный сигнал с частотой первой гармоники входного сигнала, выбирают первый временной интервал, в котором входной сигнал не изменяет свой знак, определяют середину первого временного интервала, выбирают второй временной интервал, в котором опорный синусоидальный сигнал не изменяет свой знак, определяют середину второго временного интервала, измеряют мгновенные значения входного сигнала в момент времени t1, а опорного сигнала в момент времени t2, причем моменты времени t1 и t2 выбирают равноотстоящими соответственно от середин первого и второго временных интервалов, определяют модуль отношения мгновенных значений входного и опорного сигналов, многократно определяют модули отношения мгновенных значений входного и опорного сигналов для каждой пары моментов времени, равноотстоящих от середин соответственно первого и второго временных интервалов, определяют усредненное значение модулей отношения мгновенных значений входного и опорного сигналов, а действующее значение гармонических составляющих входного сигнала определяют как корень квадратный из разности квадратов двух величин действующего значения входного сигнала и произведения действующего значения опорного синусоидального сигнала на усредненное значение модулей отношения мгновенных значений входного и опорного сигналов.
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Мирский Г.Я.Аппаратурное определение характеристик случайных процессов | |||
| - М.: Энергия, 1972, с | |||
| Крутильный аппарат | 1922 |
|
SU234A1 |
| Аппарат для очищения воды при помощи химических реактивов | 1917 |
|
SU2A1 |
| Калинчук Б.А | |||
| и др | |||
| Анализаторы инфранизных случайных процессов | |||
| - М.: Энергия, 1973, с | |||
| Способ получения бензидиновых оснований | 1921 |
|
SU116A1 |
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Способ безгетеродинного спектрального анализа сигналов | 1985 |
|
SU1287034A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| Способ гармонического анализа электрического сигнала | 1982 |
|
SU1113751A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1997-09-20—Публикация
1993-08-24—Подача