Изобретение относится к оптике и предназначено для использования в оптических приборах различного назначения.
Известны коноидные линзы, имеющие отрицательную кривизну преломляющей поверхности. Они характеризуются тем, что центры кривизны главных нормальных сечений лежат по разные стороны от преломляющей поверхности [1]
В этой конструкции экваториальное сечение имеет вид окружности, в меридиональном сечении преломляющая поверхность также образуется кривой с постоянным радиусом. Поэтому в такой линзе кривизна поверхности в любой точке является переменной величиной.

где R1 радиус окружности образующей в меридиональном сечении;
R2 радиус окружности образующей в экваториальном сечении.
По этой причине традиционная коноидная линза не может строить правильного изображения.
Для устранения указанного недостатка предлагается коноидная линза, образующая поверхности которой в меридиональном сечении выполнена в виде кривой с переменным радиусом кривизны, с таким условием, чтобы кривизна поверхности коноидной линзы в любой точке ее поверхности была постоянной величиной: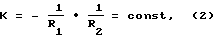
Выполнение этого условия позволяет построить тонкую коноидную линзу, способную строить правильное изображение.
Уравнение образующей поверхности вращения постоянной отрицательной кривизны имеет вид:
где a, b постоянные коэффициенты;
r текущая координата;
Z ортогональная текущая координата.
Если b < a, то из уравнения (3) видно, что r всегда меньше b.
При r b производная dz/dr 0 и касательная к образующей параллельна оси r.
В точке 0 образующая имеет точку возврата. При r 0 производная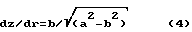
Анализ уравнения (4) показывает, что все образующие пересекают ось вращения 0 под острым углом. Поверхность вращения с образующей (3) при b < a является поверхностью вращения постоянной отрицательной кривизны эллиптического типа и имеет конечные размеры.
Таким образом, линза, построенная с применением формул (4), имеет конечную толщину и строго постоянную отрицательную кривизну преломляющей поверхности.
На фиг. 1 схематично изображена предлагаемая собирательная линза, на фиг. 2 ход лучей в линзе.
Как видно из чертежа, собирательная линза имеет отрицательную гауссову кривизну преломляющей поверхности, сечение которой в одной плоскости является окружностью, а в ортогональной плоскости ограничено кривой (3).
Анализ показал, что ход лучей в тонкой линзе с отрицательной гауссовой кривизной поверхности подчиняется законам геометрической оптики.
Лучи, падающие на линзу, преломляются таким образом, что они фокусируются в различные точки, расположенные на геометрической оси линзы (фиг. 2). Поэтому линза с отрицательной гауссовой кривизной имеет распределенное в пространстве фокусное расстояние. Длина линии распределенного фокуса определяется уравнением образующей поверхности, а также диаметром линзы.
Такая линза обладает рядом преимуществ по сравнению с традиционной коноидной линзой:
1. Коноидная линза с постоянной кривизной в любой точке поверхности строит правильное изображение.
2. Коноидная линза с постоянной кривизной поверхности обладает в 2 раза меньшим весом.
3. Коноидная линза с постоянной кривизной поверхности обладает меньшими потерями излучения за счет меньшей длины пролета фотонов в теле линзы.
| название | год | авторы | номер документа |
|---|---|---|---|
| ЛИНЗА-ФОКОН | 1992 |
|
RU2069380C1 |
| Биконоидный концентратор излучения | 2001 |
|
RU2224956C2 |
| КОНЦЕНТРАТОР СОЛНЕЧНОГО ИЗЛУЧЕНИЯ | 1994 |
|
RU2123158C1 |
| СТРОИТЕЛЬНАЯ ОПТИЧЕСКАЯ ПАНЕЛЬ | 1994 |
|
RU2099487C1 |
| ПОРТАТИВНЫЙ ГЕЛИОСВАРОЧНЫЙ АППАРАТ | 1994 |
|
RU2090329C1 |
| СТРОИТЕЛЬНАЯ СВЕТОВАЯ ПАНЕЛЬ | 1998 |
|
RU2143039C1 |
| ГРАДИЕНТНАЯ ЛИНЗА | 2005 |
|
RU2289830C1 |
| ИНТРАОКУЛЯРНАЯ ЛИНЗА С РАСШИРЕННОЙ ГЛУБИНОЙ ФОКУСА | 2020 |
|
RU2820775C1 |
| УСТРОЙСТВО ОПРЕДЕЛЕНИЯ ПОЛОЖЕНИЯ И СКОРОСТИ ПЕРЕМЕЩЕНИЯ ОПТИЧЕСКОЙ ГОЛОВКИ ЛАЗЕРНОГО ПРОИГРЫВАТЕЛЯ | 1992 |
|
RU2071612C1 |
| ИНТРАОКУЛЯРНАЯ ЛИНЗА И СПОСОБ ЛЕЧЕНИЯ ГЛАЗА | 2020 |
|
RU2815293C2 |

Использование: в оптических приборах различного назначения. Сущность изобретения: линза образована преломляющий поверхностью, сечение которой в одной плоскости является окружностью, а в перпендикулярной - кривой с переменным радиусом кривизны, описываемой уравнением  где a, b - постоянные коэффициенты, r - текущая координата, z - ортогональная текущая координата. 2 ил.
где a, b - постоянные коэффициенты, r - текущая координата, z - ортогональная текущая координата. 2 ил.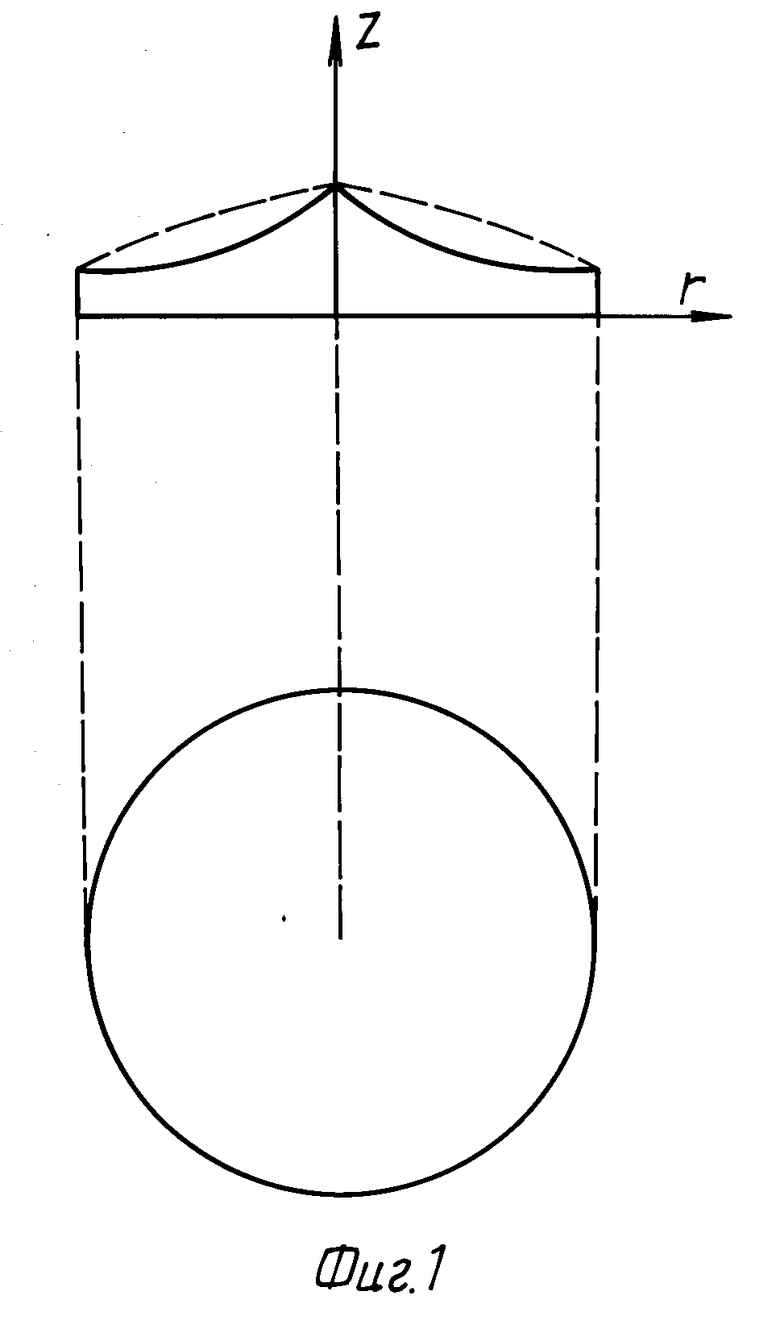
Коноидная линза, сечение преломляющей поверхности которой в одной плоскости является окружностью, а в ортогональной плоскости кривой с переменным радиусом кривизны, причем центры кривизны в сечениях лежат по разные стороны от преломляющей поверхности, отличающаяся тем, что преломляющая поверхность образована кривой, удовлетворяющей уравнению
где a и b постоянные коэффициенты;
r текучая координата;
Z ортогональная текучая координата.
| Бегунов Б.Н | |||
| и др | |||
| Теория оптических систем | |||
| -М.: Машиностроение, 1973, с | |||
| Льночесальная машина | 1923 |
|
SU245A1 |
Авторы
Даты
1997-11-10—Публикация
1992-06-09—Подача