ГРАДИЕНТНАЯ ЛИНЗА Российский патент 2006 года по МПК G02B3/00 

1. ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ

Предлагаемое изобретение относится к градиентной оптике и может быть использовано в волоконной оптике и оптическом приборостроении для создания объективов, конденсоров, эндоскопов, устройств согласования волоконно-оптических линий связи с источниками излучения и фотоприемниками и т.д.

2. УРОВЕНЬ ТЕХНИКИ

В градиентной оптике известны линзы со сфероконцентрическим градиентом показателя преломления (ПП).

Так, известна идеально фокусирующая линза со сфероконцентрическим градиентом ПП (линза Люнеберга) [1, 2], выполненная в форме сферы, в которой зависимость ПП удовлетворяет уравнению

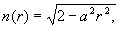
или в декартовой системе координат

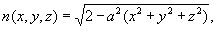
где a - постоянная;

r - расстояние от центра распределения ПП.

Входной параллельный пучок известная линза фокусирует на своей сферической поверхности на стороне, противоположной стороне падения входного пучка.

Недостатком известной линзы являются ограниченные эксплуатационные возможности, поскольку в случае, если предмет расположен на конечном расстоянии, то входной гомоцентрический расходящийся пучок уже не будет идеально сфокусирован в точку, и образуется кружок рассеяния. Кроме того, требуется материал с ПП на рабочей длине волны, в точности равный 2, что резко ограничивает также и возможности изготовления линзы из-за трудностей с подбором материала.

Наиболее близкой по совокупности существенных признаков к заявляемой является идеально фокусирующая линза со сфероконцентрическим градиентом ПП (линза Ильинского) [2], имеющая вдоль оптической оси z толщину d, ограниченная первой выпуклой и второй вогнутой преломляющими сферическими поверхностями с радиусами R₁ и R₂ соответственно, в которой центр сфероконцентрического градиента ПП совпадает с центром второй поверхности на оптической оси, а зависимость градиента ПП для материала линзы имеет вид

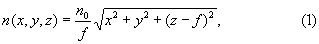
где n₀ - показатель преломления в вершине первой преломляющей поверхности;

f - заднее фокусное расстояние;

причем выполняется соотношение

f=d+s'_F',

где s'_F'=R₂ - задний фокальный отрезок (расстояние вдоль оптической оси от вершины второй поверхности до заднего фокуса).

В плоскости, проходящей через центр сфероконцентрического распределения ПП (плоскости y0z), зависимость n(x, y, z) может быть представлена как

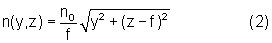
В этой известной линзе радиус первой поверхности связан с задним фокусным расстоянием следующим образом

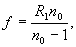
соответственно, для радиуса

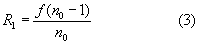
Примечание. В различных российских и зарубежных научно-технических публикациях распределение ПП, у которого поверхности равного ПП представляют собой сферы, называют как сферическим [2], так и сфероконцентрическим [3]. Ниже для определенности распределение ПП будет называться сфероконцентрическим, для отличия от формы поверхности - сферической.

Известная линза не имеет ограничений на выбор материала с заданным начальным ПП в отличие от линзы Люнеберга и точно фокусирует входной параллельный пучок (предмет в бесконечности) в точку на оси, проходящей через центр распределения ПП, но также не способна преобразовать входной расходящийся гомоцентрический пучок от предмета, находящегося на конечном расстоянии на оси, проходящей через центр распределения ПП, в выходной сходящийся гомоцентрический пучок, что часто требуется в практике. Это является недостатком известной линзы.

3. РАСКРЫТИЕ ИЗОБРЕТЕНИЯ

Задача, на решение которой направлено изобретение, - повышение эксплуатационных возможностей градиентной линзы.

Решение поставленной задачи достигается путем выполнения первой преломляющей поверхности линзы определенной формы и определения необходимого уравнения для образующей первой поверхности, в результате чего возникает возможность получать с помощью заявляемой линзы действительное безаберрационное изображение точечного предмета, находящегося на конечном расстоянии от линзы.

Для этого в градиентной линзе, имеющей вдоль оптической оси z толщину d, ограниченной первой выпуклой преломляющей поверхностью вращения с образующей у₁(z) и второй вогнутой преломляющей сферической поверхностью с радиусом R₂, имеющей сфероконцентрическое распределение показателя преломления в материале линзы, определяемое уравнением

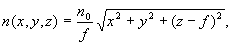
где n₀ - показатель преломления в вершине первой преломляющей поверхности;

f=d+s' - расстояние от вершины первой поверхности до центра сфероконцентрического распределения показателя преломления;

s'=R₂ - задний отрезок (расстояние вдоль оптической оси от вершины второй поверхности до осевой точки изображения);

причем центр сфероконцентрического распределения показателя преломления совпадает с центром второй поверхности на оптической оси, предусматривается, что образующая первой преломляющей поверхности в плоскости, проходящей через центр сфероконцентрического распределения показателя преломления, определяется уравнением

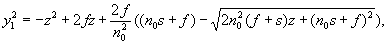
где s - передний отрезок (расстояние вдоль оптической оси от осевой точки предмета до вершины первой поверхности линзы).

Для подтверждения правильности предложенных соотношений в заявляемой градиентной линзе рассмотрим ход лучей в ней при преломлении на ее первой поверхности (фиг.1).

Линза толщиной d, выполненная из материала со сфероконцентрическим распределением ПП n(x, y, z), известным для заданной длины волны, и ограниченная первой преломляющей поверхностью вращения с образующей y₁(z) и второй сферической преломляющей поверхностью с радиусом R₂=s', расположена в однородной среде (примем ПП однородной среды n₁=1 (воздух)). Вершина первой поверхности расположена в начале координат. Ось z представляет собой оптическую ось линзы. Принимая, что линза обладает осевой симметрией, рассмотрение проводится в меридиональной плоскости, проходящей через центр распределения ПП (плоскость y0z). Соответственно, для распределения ПП в плоскости y0z можно рассматривать зависимость n(y, z).

Луч падающего на первую поверхность пучка, выходящего из точки М на оптической оси, имеет направляющий коэффициент u_K, преломляется в точке А с координатами z_П, y_П и после преломления получает направление, характеризующееся направляющим коэффициентом u_B. Угол падения луча на первую поверхность обозначим как ε, угол преломления - как ε', а нормаль к первой поверхности в точке А - как N.

Расстояние между точкой М и вершиной первой поверхности линзы является передним отрезком s.

После преломления в точке А луч движется в материале линзы по прямой, поскольку его траектория совпадает с радиусом, выходящим из центра сфероконцентрического распределения ПП, затем падает нормально на вторую сферическую поверхность, не испытывая преломления, после чего, попадая вновь в однородную среду (воздух) и не меняя своего направления, пересекает оптическую ось в точке М'.

Расстояние между вершиной второй поверхности линзы и точкой М' является задним отрезком s'.

Направляющий коэффициент u_H нормали N к образующей первой поверхности в точке А можно выразить в виде

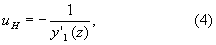
где y'₁(z) - первая производная от y₁(z).

Значение u_K определяется из выражения

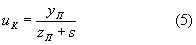
Угол падения луча можно определить по формуле [4]

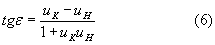
Соответственно, используя известное соотношение [4], можно вычислить

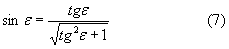
По закону преломления

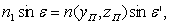
где n(y_П, z_П) - ПП в точке преломления А.

Тогда (с учетом того, что n₁=1) угол преломления выразится в виде

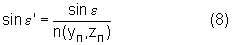
Пользуясь известным соотношением [4], получим

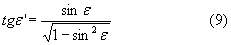
Угол преломления может быть также выражен следующим образом [4]:

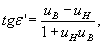
откуда

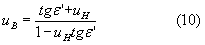
Подставив в (10) выражение (9), получим

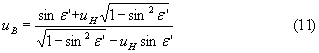
Учитывая (8) и подставляя в (11), имеем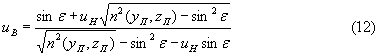

Если подставить в полученное уравнение (12) выражение (7), получим

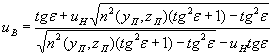
Подставляя в полученное уравнение выражение (6), получим

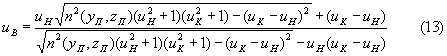
Для точного фокусирования в точке М луч после преломления в точке А должен иметь направляющий коэффициент

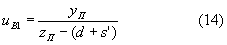
Приравняв (13) и (14), можно получить уравнение, связывающее основные параметры линзы. Выразим из уравнения (13) распределение ПП. Для этого преобразуем его следующим образом:

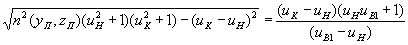
Далее, после несложных преобразований можно получить

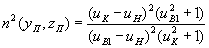
или, после извлечения квадратного корня,

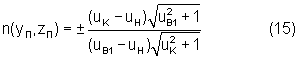
Если в (15) подставить (4), (5) и (14) и перейти к координатам, то получим

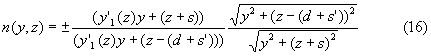
У сфероконцентрического распределения ПП поверхностями равного показателя преломления являются сферы, а при рассмотрении в плоскости, проходящей через центр распределения ПП (как в рассматриваемом случае), - окружности. Если зафиксировать значение ПП n(y, z)=n_R=const, то окружность должна иметь соответствующий радиус R, а центр ее должен располагаться в центре распределения ПП на расстоянии

от начала координат на оси z.

С учетом (17) выражение (16) можно переписать

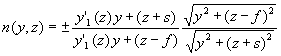
Зафиксировав значение ПП, получим

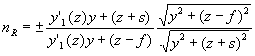
или

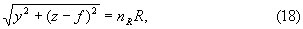
где

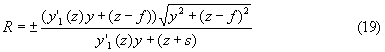
Уравнение (18) можно записать в следующем виде

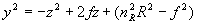
Это уравнение окружности с центром на оси z, смещенным в сторону возрастания z на расстояние f,

имеющей радиус R_N=n_RR.

Зададим для полученного распределения ПП, как и в [2], начальное условие

n(0,0)=n₀

Таким образом, в случае, если окружность касается начала координат, должно выполняться

n² ₀R²-f²=0

Тогда величина R определяется из выражения

Учитывая (20), обратимся к разрешению выражения (19), которое нетрудно преобразовать к виду

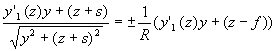
В полученном выражении вполне логично принять y=y₁(z), тогда получим

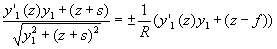
Легко заметить, что левая и правая части этого уравнения - полные производные соответственно, можно записать

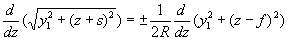
Интегрирование дает

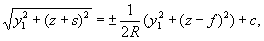
где с - постоянная интегрирования.

Исходя из начального условия для образующей

y₁(0)=0,

можно определить постоянную интегрирования

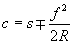
Тогда уравнение образующей примет вид

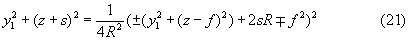
Нетрудно показать, что уравнение (21) преобразуется в биквадратное уравнение

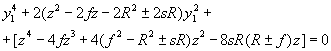
решения которого можно выразить

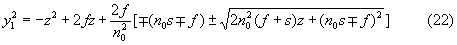
Таким образом, образующая представляет собой поверхность 4-го порядка. Соответствующее распределение ПП можно получить из выражения (16), с учетом принятого выше соотношения y=y₁(z), в виде

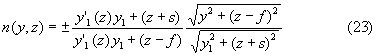
Вычислив производную от (22), подставив ее и (22) в (23) и учитывая положительность значения ПП, получим

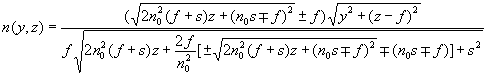
Для определенного выбора знака в полученном распределении ПП и соответствующей образующей были проведены численные расчеты хода лучей. Согласно полученным результатам необходимо выбрать знак "плюс" (для знака "минус" кривизна получающейся образующей оказывается недостаточной для точной фокусировки лучей). Тогда верное распределение ПП будет иметь вид

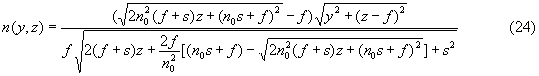
Соответствующее уравнение образующей

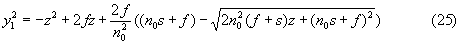
Радиус кривизны образующей при вершине

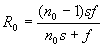
Можно отметить, что в предельном случае при s→∞ выражение для радиуса совпадает с формулой, определяющей радиус первой сферической поверхности (3) для идеально фокусирующей линзы [2]. Действительно,

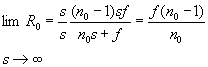
Внимательный анализ довольно громоздкого уравнения (24) приводит к выводу о возможности упрощения этого уравнения. Для этого представим (24) в виде

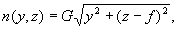
где

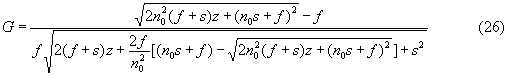
Определим условия, при которых G=const. После несложных преобразований из (26) можно получить

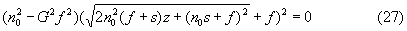
В верное равенство полученное выражение (27) обращается только в случае

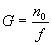
Или, другими словами, уравнение (26) сокращается до полученного выражения.

Тогда уравнение (24) значительно упрощается и его можно записать в виде

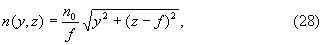
при этом оно, как нетрудно заметить, полностью совпадает с известным распределением (2).

При y=0 и z=d значение ПП, с учетом (17)

Если перейти от меридионального сечения к трем координатам, выражение для сфероконцентрического распределения ПП (28) примет вид, совпадающий с (1)

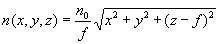
Таким образом, применение первой преломляющей поверхности с образующей (25) позволит обеспечить точную фокусировку на выходе выпукло-вогнутой линзы с известным сфероконцентрическим распределением ПП (1), в результате чего каждый луч входного гомоцентрического расходящегося пучка с центром на оптической оси после прохождения через линзу сфокусируется в заданной точке на оптической оси, осуществив преобразование входного гомоцентрического расходящегося пучка в выходной гомоцентрический сходящийся пучок и построив действительное безаберрационное изображение точечного предмета. Это расширяет эксплуатационные возможности градиентной линзы.

4. КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

На фиг.1 показаны схема преломления луча на первой поверхности градиентной линзы в меридиональной плоскости, проходящей через центр сфероконцентрического распределения ПП, и условные обозначения для расчета хода луча.

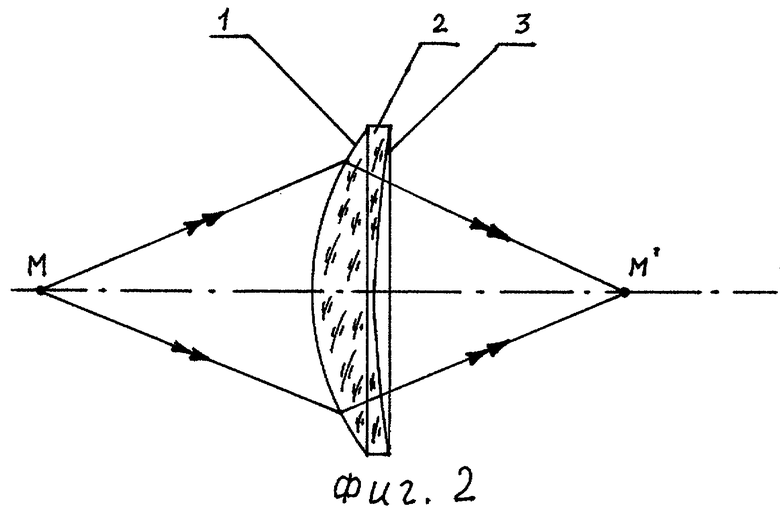
На фиг.2 показаны оптическая схема градиентной линзы в меридиональной плоскости, проходящей через центр сфероконцентрического распределения ПП, и ход лучей в линзе.

Двойными стрелками на фиг.1 и 2 показан ход лучей.

5. ОСУЩЕСТВЛЕНИЕ ИЗОБРЕТЕНИЯ

Для реализации предложенной градиентной линзы вначале определяются необходимые параметры оптической схемы и линзы - d, R₂, s, s', n₀.

Затем рассчитывается на основе уравнений (1) и (17) сфероконцентрическое распределение ПП и определяется граничное значение ПП n_d согласно (29). В зависимости от предполагаемого способа формирования градиента в материале подбирается исходная заготовка и компоненты для формирования требуемого распределение ПП. Необходимо отметить, что выбранные способ и исходный материал должны допускать достижение рассчитанного перепада значения ПП от n₀ до n_d. После этого рассчитанное сфероконцентрическое распределение ПП формируется одним из известных способов.

Среди известных способов формирования сфероконцентрического распределения ПП можно, например, отметить способ управляемого ионной диффузии (для стекол [5]) и способ управляемой диффузии мономера с последующей полимеризацией (для полимеров [6]).

Полученная заготовка со сформированным сфероконцентрическим распределением ПП подвергается обычной обработке по одной из известных оптических технологий для формообразования второй сферической преломляющей поверхности, например последовательной шлифовке и полировке.

Для формообразования первой преломляющей поверхности 4-го порядка могут использоваться известные способы получения асферических поверхностей, например, путем последовательной шлифовки и полировки или путем применения абразивной технологии с последующей ионной ретушью поверхностей [7] до достижения формы поверхности в соответствии с (25).

В качестве исходных данных для численного расчета хода лучей были приняты значения для стеклянных микролинз, ранее использованные в [2]: n₀=1,6; n_d=1,52; d=0,25 мм; s'=R₂=4,75 мм. Разница между значениями ПП n₀ и n_d, как указано в [2], вполне может быть достигнута при современном уровне технологии. Для переднего отрезка предлагаемой линзы было принято значение s=5,0 мм, соответственно радиус кривизны образующей при вершине для первой поверхности составил R₀=1,153 мм. Значение R₀ меньше, чем значение радиуса R₁=1,875 мм первой сферической поверхности в идеально фокусирующей линзе [2], что физически вполне объяснимо, поскольку в предлагаемой линзе углы падения лучей на первую поверхность больше при одинаковых углах преломления и кривизна поверхности также должна быть больше.

Можно отметить, что, поскольку радиус кривизны образующей R₀ меньше, чем f=d+s', то при формировании требуемого распределения ПП удобно использовать исходную заготовку в виде сферы радиуса порядка f, из которой после завершения процесса формировании распределения ПП можно вырезать несколько рабочих заготовок линз для последующего формообразования преломляющих поверхностей.

В приложении приведены последовательность и результаты численных расчетов хода лучей, подтверждающие гомоцентрический ход лучей на выходе заявляемой линзы.

Используется предлагаемая градиентная линза обычным образом. В точку М перед первой поверхностью 2 линзы 1 (фиг.2) помещается точечный источник излучения. После преломления на первой поверхности и прохождения внутри линзы гомоцентрический пучок излучения, преломляясь на второй поверхности 3 линзы, выходит из нее, оставаясь гомоцентрическим, и фокусируется в точке М'.

Предложенная градиентная линза может быть использована как отдельно, например, в качестве устройства сопряжения оптических волоконных световодов с источниками излучения (полупроводниковыми лазерами, светодиодами) и приемниками излучения (фотодиодами), в качестве конденсора, объектива и т.п., так и в составе более сложной оптической системы.

6. ИСТОЧНИКИ ИНФОРМАЦИИ

1. Luneburg R.К. Mathematical theory of optics Berkeley, CA: University of California Press, 1964.

2. Roman Ilinsky. Gradient-index meniskus lens free of spherical aberration - Journal of Optics A: Pure and Applied Optics, Volume 2, Number 5, September 2000, pp.449-451.

3. Вычислительная оптика. Справочник / Под ред. М.М.Русинова - М., Машиностроение, 1984, 423 с.

4. Выгодский М.Я. Справочник по высшей математике. 1-е изд. - М., Наука, 1972, 870 с.

5. David J. Fischer, Curtis J. Harkrider, Duncan T. Moore. Design and manufacture of a gradient-index axi-con - Applied Optics, Vol.39, No.16, 1 June 2000, pp.2687-2694.

6. Косяков В.И., Тухватулин А.Ш., Фадеев Е.А. Математическое моделирование технологии и свойств градиентных сферических линз - Журнал технической физики, 1998, том 68, №10, стр.70-73.

7. Государственный оптический институт им. С.И.Вавилова. Официальный сайт в сети Интернет. Информация по адресу http://soi.srv.pu.ru/r_1251/developments/technology/ap_ktf.htm

Приложение

1. Методика проведения расчетов

1.1. Общие условия

Целью проведения расчетов является подтверждение точной фокусировки лучей на выходе заявляемой линзы.

Для расчетов используется схема фиг.1 заявки, расчеты проводились для меридиональной плоскости y0z, проходящей через центр сфероконцентрического распределения показателя преломления (ПП), численные значения даны в миллиметрах, результаты приведены с точностью до семи значащих цифр.

Исходными данными для расчета хода лучей и параметров линзы являются:

1) закон распределения показателя преломления

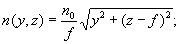
6) уравнение образующей 1-й поверхности линзы

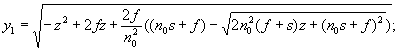
2) значения ПП в вершине 1-й поверхности n₀=1,60;

3) толщина линзы d=0,25 мм;

4) задний отрезок s'=R₂=4,75 мм, равный радиусу второй сферической поверхности;

5) передний отрезок s=5,0 мм.

Допущение - не рассчитывается траектория хода лучей после преломления на 1-й поверхности, вычисляется только реальный и идеальный направляющие коэффициенты луча после преломления на 1-й поверхности.

Указанное допущение рационально сокращают объем расчетов и основано на прямолинейном ходе преломленных на 1-й поверхности лучей, что обосновано в описании.

1.2. Последовательность расчетов

1. Определяются постоянные

f=d+s',

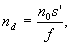
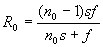
1. Для текущего значения координаты z_т определяется значение координаты у_1T

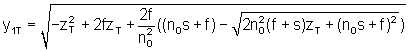
2. Определяется значение показателя преломления на данной высоте входного луча у_1T

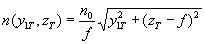
4. Определяется значение производной y'_1T(z_T) для образующей 1-й поверхности в точке преломления А

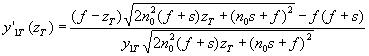
5. Определяется значение направляющего коэффициента нормали в точке преломления А

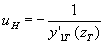
6. Определяется значение направляющего коэффициента входного луча

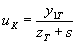
7. Рассчитывается угол падения

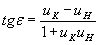
8. Затем вычисляется

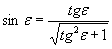
9. Определяется угол преломления

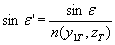
10. Затем вычисляется

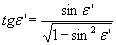
11. Рассчитывается реальный направляющий коэффициент u_B преломленного на 1-й поверхности входного луча

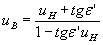
6. Определяется идеальным значение U_B0 направляющего коэффициента выходного луча

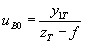
23. Определяется разница между полученным в результате преломления u_B и идеальным u_B0 значениями направляющего коэффициента выходного луча

Δ=u_B-u_B0,

которая, согласно замыслу, должна быть равна нулю.

2. Результаты расчетов

Постоянные величины:

f=d+s'=5,0 мм; n_d=1,52; R₀=1,153 мм

Преломление лучей на первой поверхностиz_тy_1Tu_Ku_нtgεsinεn(y_1T,z_T)0,010,1517733,029404E-2-1,320158Е-11,629615Е-11,608399Е-11,5975380,020,2144444,271790E-2-1,872143Е-12,317859Е-12,257998Е-11,5950760,030,2623985,216661Е-2-2,299304Е-12,855218Е-12,745500Е-11,5926150,040,3027126,006181Е-2-2,662508Е-13,316157Е-13,147601Е-11,5901530,050,3381286,695594Е-2-2,985278Е-13,729381Е-13,494291Е-11,5876910,060,3700547,313323Е-2-3,279652Е-14,109553Е-13,801096Е-11,5852290,070,3993297,876305Е-2-3,552772Е-14,465355Е-14,077323Е-11,5827660,080,4264978,395607Е-2-3,809284Е-14,802433Е-14,329093Е-11,5803040,090,4519388,878944Е-2-4,052411Е-15,124698Е-14,560695Е-11,5778410,100,4759299,331947Е-2-4,284501Е-15,435002Е-14,775282Е-11,5753780,110,4986799,758883Е-2-4,507323Е-15,735495Е-14,975252Е-11,5729150,120,5203491,016307Е-1-4,722252Е-16,027852Е-15,162486Е-11,5704520,130,5410701,054717Е-1-4,930385Е-16,313410Е-15,338492Е-11,5679880,140,5609461,091334Е-1-5,132609Е-16,593257Е-15,504500Е-11,5655240,150,5800631,126335Е-1-5,329657Е-16,868296Е-15,661535Е-11,5630600,160,5984941,159871Е-1-5,522145Е-17,139286Е-15,810457Е-11,5605960,170,6163001,192068Е-1-5,710592Е-17,406878Е-15,952001Е-11,5581310,180,6335331,223035Е-1-5,895446Е-17,671633Е-16,086796Е-11,5556660,190,6502381,252867Е-1-6,077093Е-17,934041Е-16,215393Е-11,5532000,200,6664551,281644Е-1-6,255872Е-18,194539Е-16,338270Е-11,5507340,210,6822191,309440Е-1-6,432081Е-18,453513Е-16,455850Е-11,5482680,220,6975591,336319Е-1-6,605984Е-18,711313Е-16,568508Е-11,5458010,230,7125031,362338Е-1-6,777817Е-18,968255Е-16,676580Е-11,5433340,240,7270751,387546Е-1-6,947794Е-19,224631Е-16,780364Е-11,5408660,250,7412961,411991Е-1-7,116106Е-19,480709Е-16,880132Е-11,538398

Продолжение таблицыz_Tsinε'tgε'u_Вu_В0Δ0,011,006798E-11,011940Е-1-3,041546Е-2-3,041546Е-2-3,469446Е-180,021,415604Е-11,430005Е-1-4,306102Е-2-4,306102Е-26,938893Е-180,031,723894Е-11,750095Е-1-5,279639Е-2-5,279639Е-2-5,551115Е-170,041,979432Е-12,019389Е-1-6,103054Е-2-6,103054Е-20,00,052,200863Е-12,256184Е-1-6,830858Е-2-6,830858Е-2-2,775557Е-170,062,397821Е-12,469875Е-1-7,490975Е-2-7,490975Е-21,387778Е-170,072,576073Е-12,666053Е-1-8,099973Е-2-8,099973Е-2-5,551115Е-170,082,739404Е-12,848364Е-1-8,668635Е-2-8,668635Е-28,326672Е-170,092,890464Е-13,019345Е-1-9,204445Е-2-9,204445Е-21,387778Е-170,103,031196Е-13,180847Е-1-9,712843Е-2-9,712843Е-2-1,387778Е-170,113,163076Е-13,334268Е-1-1,019793Е-1-1,019793Е-1-1,387778Е-170,123,287260Е-13,480699Е-1-1,066289Е-1-1,066289Е-14,163336Е-170,133,404674Е-13,621007Е-1-1,111026Е-1-1,111026Е-18,326672Е-170,143,516073Е-13,755896Е-1-1,154209Е-1-1,154209Е-16,938893Е-170,153,622082Е-13,885949Е-1-1,196005Е-1-1,196005Е-12,775557Е-170,163,723229Е-14,011654Е-1-1,236557Е-1-1,236557Е-1-4,163336Е-170,173,819960Е-14,133423Е-1-1,275982Е-1-1,275982Е-15,551115Е-170,183,912662Е-14,251611Е-1-1,314382Е-1-1,314382Е-15,551115Е-170,194,001667Е-14,366524Е-1-1,351846Е-1-1,351846Е-10,00,204,087269Е-14,478429Е-1-1,388448Е-1-1,388448Е-10,00,214,169722Е-14,587561Е-1-1,424256Е-1-1,424256Е-15,551115Е-170,224,249257Е-14,694128Е-1-1,459328Е-1-1,459328Е-1-1,665334Е-160,234,326074Е-14,798313Е-1-1,493716Е-1-1,493716Е-1-2,775557Е-170,244,400357Е-14,900283Е-1-1,527467Е-1-1,527467Е-15,551115Е-170,254,472268Е-15,000185Е-1-1,560622Е-1-1,560622Е-1-8,326672Е-17

3. Краткие выводы

Приведенные результаты расчетов хода лучей в заявляемой линзе показывают, что

1) лучи, преломленные на 1-й поверхности линзы, образуют гомоцентрический пучок (отклонение величины Δ от нуля в таблице определяется только погрешностью машинного расчета);

3) точная фокусировка лучей на выходе заявляемой линзы подтверждается.

Изобретение относится к градиентной оптике и может быть использовано в волоконной оптике и оптическом приборостроении. Градиентная линза имеет вдоль оптической оси z толщину d, ограничена первой выпуклой преломляющей поверхностью вращения с образующей y₁(z) и второй вогнутой преломляющей сферической поверхностью с радиусом R₂ и имеет сфероконцентрическое распределение показателя преломления в материале линзы, определяемое уравнением 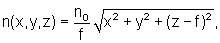где n₀ - показатель преломления в вершине первой преломляющей поверхности; f=d+s' - расстояние от вершины первой поверхности до центра сфероконцентрического распределения показателя преломления; s'=R₂ - задний отрезок. Центр сфероконцентрического распределения показателя преломления совпадает с центром второй поверхности на оптической оси. Образующая первой преломляющей поверхности в плоскости, проходящей через центр сфероконцентрического распределения показателя преломления, определяется уравнением 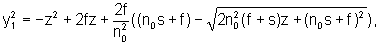где s - передний отрезок. Линза преобразует входной расходящийся гомоцентрический пучок от предмета, находящегося на конечном расстоянии на оси, в выходной сходящийся гомоцентрический пучок, фокусирующийся в центре распределения показателя преломления. Технический результат - повышение эксплуатационных возможностей. 2 ил., 1 прилож., 1 табл.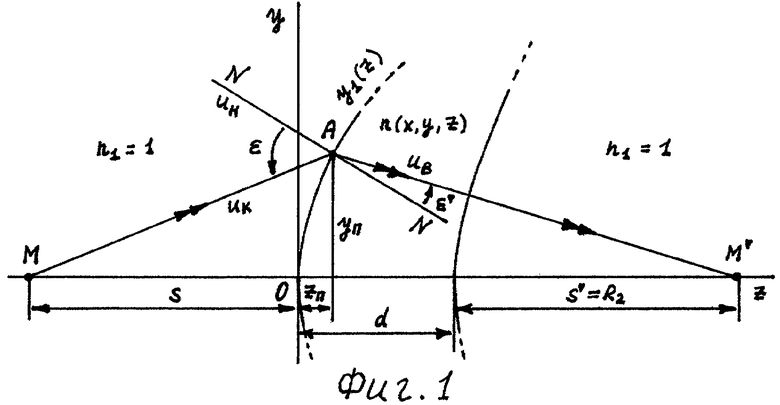

Градиентная линза, имеющая вдоль оптической оси z толщину d, ограниченная первой выпуклой преломляющей поверхностью вращения с образующей y₁(z) и второй вогнутой преломляющей сферической поверхностью с радиусом R₂, имеющая сфероконцентрическое распределение показателя преломления в материале линзы, определяемое уравнением

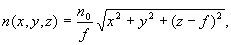
где n₀ - показатель преломления в вершине первой преломляющей поверхности;

f=d+s' - расстояние от вершины первой поверхности до центра сфероконцентрического распределения показателя преломления;

s'=R₂ - задний отрезок;

причем центр сфероконцентрического распределения показателя преломления совпадает с центром второй поверхности на оптической оси, отличающаяся тем, что образующая первой преломляющей поверхности в плоскости, проходящей через центр сфероконцентрического распределения показателя преломления, определяется уравнением

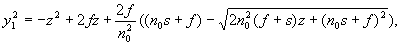
где s - передний отрезок.