Изобретение относится к гамма-дефектоскопии и может быть использовано при неразрушающем контроле качества ответственных деталей в реакторной, авиационной и ракетной техники, а также в медицинской гамма-диагностике.
В качестве аналога рассмотрен известный в оптике способ оптического стереоскопического зрения (ОСЗ), например стереоскопического зрения человека [1] Этот способ не может быть использован в гамма-стереоскопии ввиду оптической непрозрачности анализируемых материалов.
В качестве прототипа рассмотрен известный способ комптоновской гамма-дефектоскопии, включающий облучение изучаемого объекта зондирующими гамма-квантами и измерение распределения интенсивности рассеянного излучения в зависимости от положения точки зондирования в плоскости сканирования объекта [2,3] который позволяет получать информацию об электронной плотности объекта в плоскости,перпендикулярной направлению зондирования, и не может обеспечить получение такой информации вдоль направления зондирования, поскольку в нем не предусмотрено формирование внутри объекта протяженного квазиодномерного зондирующего пучка зондирующих фотонов (ПЗФ), рассеяние которых только и может обеспечить получение стереоскопической информации, получение стереоскопической информации ограничено коллиматором детектора, т.е. малой апертурой регистрации рассеянного излучения,линейное разрешение вдоль ПЗФ ограничено энергетическим разрешением спектрометрического детектора (СД).
Целью изобретения является определение электронной плотности объекта в направлении (вдоль) луча зондирования.
Поставленная цель достигается тем, что внутри изучаемого объекта формируют протяженный квазиодномерный пучок зондирующих фотонов и измеряют распределение интенсивности комптоновски рассеянных фотонов вдоль пучка зондирования.
На фиг. 1 схематически изображено сравнение схем способа оптического стереоскопического зрения (ОСЗ) и возможного однодетекторного способа комптоновского стереоскопического зондирования (КСЗ). Разрешающая способность ω = ω1 = ω2 (радиан) обеспечивает в оптике при базовом расстоянии между L и R, равном b0, возможность различить две равноудаленные на расстояние l от наблюдателя точки B и D [1] Согласно геометрии, величина разноудаленных точек AB ΔrA и СД = Δrc (C и D стереоскопически различимые точки) определена формулами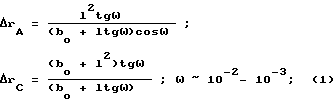
Разрешающая сила ОСЗ на произвольном расстоянии оценивается величиной стереодиоптрии, равной
где b0 и l выражены в метрах. Здесь W0 м-1 оценка числа различимых объектов на глубине пространства, равной 1 м, удаленного от наблюдателя на расстояние l метров [1] Такая оценка в ОСЗ справедлива при естественном условии b0 ≈ l, w << 1. Следует отметить, что в ОСЗ необходим внешний источник света.
В случае КСЗ следует принять b0 ≈ l, w < 1, так что в КСЗ разрешающую силу следует оценивать по формуле (полагая, что w = ω1≥ ω2, ω2 угловая расходимость ПЗФ)
Кроме того, следует учесть, что в КСЗ необходимо формировать внутри объекта достаточно протяженный ПЗФ, что возможно лишь в относительно легких материалах; так, например, для E0 ≈ 511 кэВ эта возможность ограничена вблизи титана (Z 22, d 4,5 г/см3). Следует отметить, что в КСЗ внешний источник излучения, подобный свету в ОСЗ, не нужен.
Разрешающую способность в КСЗ можно вычислить, используя вытекающую из геометрии фиг. 1 формулу ω = ν2 - ν1, которая связывает ω с углами комптоновского рассеяния, а также используя классическую формулу А. Комптона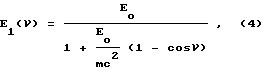
связывающую энергию рассеянного фотона E1 с энергией зондирующего фотона E0 и углом рассеяния ν(mc2 511 кэВ энергия, равная массе покоя электрона):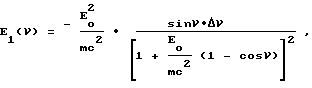
Полагая для простоты E0 mc2, получаем оценку разрушающей силы в КСЗ при зондировании позитрон-аннигиляционными фотонами: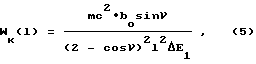
где под ΔE1 теперь следует понимать энергетическое разрешение спектрометрического детектора (СД),размещенного в точке L на фиг.1. Используя типичное значение E1 2 кэВ и V > π /2 для КСЗ и w ≈ 10-2 10-3 для ОСЗ нетрудно показать, что Wk(l) ≈ W0(l).
Эта оценка демонстрирует принципиальную возможность достичь удовлетворительное стереоскопическое разрешение (порядка разрешения ОСЗ человека) в однодетекторной схеме КСЗ.
Однако практическая реализация рассмотренной однодетекторной схемы КСЗ осложнена рядом обстоятельств: малой геометрической светосилой регистрации рассеянных фотонов,ограничением стереоскопического разрешения за счет аппаратурного энергетического разрешения СД,ограничением стереоскопического разрешения за счет энергетического распределения зондирующих фотонов. Последнее ограничение имеет отношение к способам зондирования позитрон - аннигиляционными или тормозными фотонами, например, для позитрон-аннигиляционных фотонов DEo ~ ΔE1 ~ 2 кэВ, тогда как при зондировании ядерными гамма-квантами уширением зондирующих фотонов ΔEo ≈Г ≅10-5 эВ всегда можно пренебречь.
Сущность предлагаемого изобретения заключается в том, что вместо одного спектрометрического детектора, размещенного в точке L на фиг.1, используют несколько (десятков) неспектрометрических детекторов, НД, расположенных вдоль пучка зондирования, что увеличивает геометрическую светосилу, и либо ослабляет требования к энергетическому разрешению детекторов рассеянного излучения (при гамма-локационном зондировании), либо позволяет использовать только неспектрометрические счетчики рассеянных фотонов (при зондировании ядерными гамма-квантами).
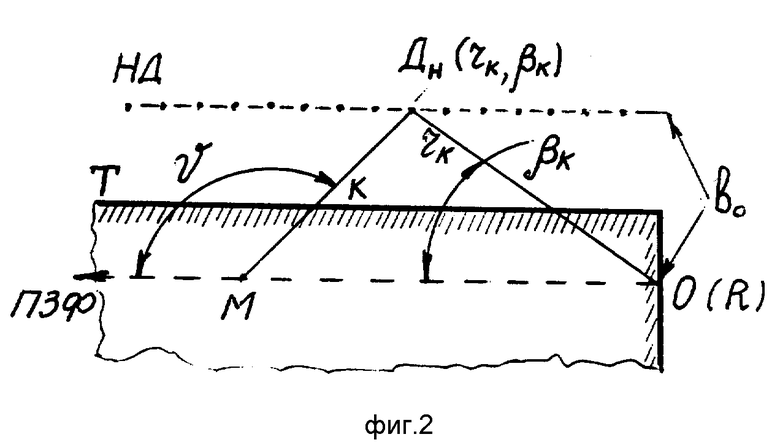
На фиг. 2 изображена схема одного из вариантов предлагаемого способа КСЗ многодетекторного КСЗ. Пучок зондирующих фотонов ПЗФ попадает в анализируемый объект в точке О и проходит внутри объекта параллельно его поверхности Т (которая перпендикулярна плоскости фиг. 2). Базовое расстояние b0 фиксирует положение неспектрометрических детекторов Dн (rk, βк K 1, 2, n, b0 rksin  , где rk линейное расстояние K-того детектора от точки О, а угол βк -угол между направлением ПЗФ и rk. Зондирующий фотон с энергией E0 однократно рассеивается в точке M на глубине l OM и попадает в один из детекторов Dн (rk, бетаk). В этой схеме характерные длины и углы К-того детектора связаны с энергией рассеянного фотона E1(V) следующими соотношениями:
, где rk линейное расстояние K-того детектора от точки О, а угол βк -угол между направлением ПЗФ и rk. Зондирующий фотон с энергией E0 однократно рассеивается в точке M на глубине l OM и попадает в один из детекторов Dн (rk, бетаk). В этой схеме характерные длины и углы К-того детектора связаны с энергией рассеянного фотона E1(V) следующими соотношениями: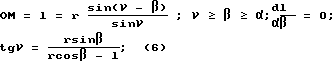
где α угол между плоскостью Т и ПЗФ; для варианта, изображенного на фиг. 2 a 0. Для аннигиляционных фотонов E0 mc2: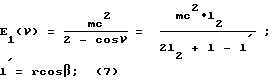
Мы хотим теперь показать, что информация об электронной плотности объекта, получаемая в однодетекторной схеме КСЗ (фиг. 1) адекватна информации, получаемой в многодетекторной схеме КСЗ (фиг. 2), за исключением некоторых аппаратурных ограничений, присущих схеме фиг.1 (ограничения по светосиле и по энергетическому разрешению СД). Для этого допустим на некоторое время, что в схеме фиг. 2 регистрация рассеянного излучения выполняется только одним детектором Dс (rc, 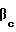 ), причем этот детектор - спектрометрический (что делает на это время схему фиг. 2 адекватной схеме фиг. 1), и запишем выражение для энергетического (или, что согласно (4), (7) эквивалентно для углового) распределения фотонов, зарегистрированных этим детектором в телесном угле ΔΩ = 2πssinνΔν(2πc апертура детектора, s < 1):
), причем этот детектор - спектрометрический (что делает на это время схему фиг. 2 адекватной схеме фиг. 1), и запишем выражение для энергетического (или, что согласно (4), (7) эквивалентно для углового) распределения фотонов, зарегистрированных этим детектором в телесном угле ΔΩ = 2πssinνΔν(2πc апертура детектора, s < 1):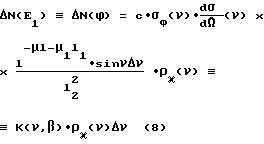
где 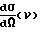 дифференциальное сечение комптоновского рассеяния (сечение Кляйна-Нишины-Тамма [4] ), sф(ν) ≡ σф(E1) сечение фотопоглощения [4] рассеянных фотонов с энергией E1(V) в детекторе, μ(Eo), μ1(E1) линейные коэффициенты поглощения зондирующих (E0) и рассеянных (E1) фотонов в материале объекта, l1 MK расстояние, проходимое рассеянным фотоном в материале объекта (фиг. 2), l2 расстояние от точки рассеяния М до точки регистрации Dс (rc,бетаc), а ρκ(ν) ≡ ρκ(l) искомое распределение электронной плотности, которое можно моделировать, например, с помощью функции:
дифференциальное сечение комптоновского рассеяния (сечение Кляйна-Нишины-Тамма [4] ), sф(ν) ≡ σф(E1) сечение фотопоглощения [4] рассеянных фотонов с энергией E1(V) в детекторе, μ(Eo), μ1(E1) линейные коэффициенты поглощения зондирующих (E0) и рассеянных (E1) фотонов в материале объекта, l1 MK расстояние, проходимое рассеянным фотоном в материале объекта (фиг. 2), l2 расстояние от точки рассеяния М до точки регистрации Dс (rc,бетаc), а ρκ(ν) ≡ ρκ(l) искомое распределение электронной плотности, которое можно моделировать, например, с помощью функции: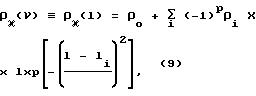
в которой P 1 для 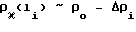 и P 2 для
и P 2 для 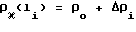 , Δρi приращение плотности вблизи i-того дефекта, ρi "амплитуда" дефекта, Δi его "полуширина". Константа C в (8) исчезает при естественной нормировке спектра
, Δρi приращение плотности вблизи i-того дефекта, ρi "амплитуда" дефекта, Δi его "полуширина". Константа C в (8) исчезает при естественной нормировке спектра 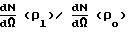 где, как и в (9), ρo бездефектная плотность объекта, а ρl ≡ ρκ(l).
где, как и в (9), ρo бездефектная плотность объекта, а ρl ≡ ρκ(l).
Согласно (8) и (9), дефект электронной плотности в точке l=li(v)=li(Ei) проявляется в виде "пика" (P 2) или "провала" (P 1) в энергетическом (угловом) спектре фотонов (8).
Вычислим полное число рассеянных фотонов F(bc), зарегистрированных рассматриваемым спектрометрическим детектором Dс (rc, βc ) в схеме фиг. 2: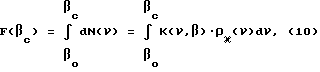
где βo максимальный угол ν, определяемый длиной ПЗФ; вследствие (4) интегрирование (10) по углу адекватно интегрированию по энергии E1(V). Такое же число рассеянных фотонов F(bc) было бы зарегистрировано и в том случае, если бы вместо спектрометрического Dс (rc, βc) (при прочих равных параметрах) мы использовали неспектрометрический Dн (rc, βc), поскольку интегрирование энергетического спектра по энергии E1(V) полностью нивелирует его спектрометрические проявления. Поскольку число фотонов,зарегистрированных таким неспектрометрическим детектором, является только функцией βк (вследствие b0 rksin βк Const), то используя (10), его всегда можно вычислить из соотношения: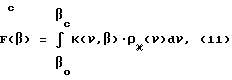
Допустим теперь, что согласно схеме фиг.2, все детекторы Dн (rk, βк) неспектрометрические и в результате эксперимента получена серия значений F(βк). Тогда, чтобы определить распределение электронной плотности вдоль направления зондирования ρκ(ν) ≡ ρκ(l) следует выполнить следующие операции.
Построить по точкам F(bк) интерполяционный многочлен F(β) целую [5] дифференцируемую функцию (см. также [6]).
Исключить поправки на многократное рассеяние зондирующих фотонов [7] см. также [6]
Рассматривая соотношение (11) как интегральное уравнение Вольтерра 1-го рода [8] дополнить его интегрируемое ядро K(ν,β) до фредгольмова ядра [8] преобразовать полученное уравнение Фредгольма [8] к системе линейных уравнений и решить эту систему (на компьютере) относительно ρκ(ν).
В случае необходимости учет энергетического распределения зондирующих (например, позитрон-аннигиляционных) фотонов выполняют усреднением ядра K(ν,β) ≡ K(Eo, ν, β) по известному спектру (полученному экспериментально, например методом измерения угловых корреляций аннигиляционных фотонов) f(E0) зондирующих фотонов (эту процедуру можно выполнить в (8) и в (11).
Согласно теории Фредгольма [8] интегральное уравнение (11) с интегрируемым ядром K(ν,β) имеет однозначное решение, если функции K(v, β) и F(бета) дифференцируемы и функция K(ν,ν) ≡ K(β,β) ≠ 0.
В рассматриваемом случае эти условия всегда выполняются, поскольку F(β) целая [5] функция (по построению пункт 1), а функция K(ν,β) произведение целых функций. Физическая основа однозначности решения интегрального уравнения (11) заключается в том, что в рассматриваемых процессах рассеяния и регистрации участвуют только значения конечных вероятностей и конечного числа частиц (отсутствует физическая причина появления "расходимостей").
Предлагаемый способ КСЗ обеспечивает наивысшую геометрическую светосилу регистрации рассеянных фотонов и исключает ограничения, связанные с конечным энергетическим разрешением спектрометрических детекторов. Основные ограничения этого способа связаны с возможной (в случае зондирования аннигиляционными фотонами) немонохроматичностью ПЗФ и статистической ошибкой при измерении F(βк), а также с погрешностью определения координат βк, (т. е. всегда связаны с точностью интерполяции функции F(β)). С ростом числа используемых неспектрометрических детекторов n точность интерполяции возрастает и при n ≈ 20-30 заведомо превышает возможную статистическую точность и точность определения координат βк. Малые значения n ≈ 4-5 ограничивают аппаратурную точность. Оптимальные значения n нами не оценивались, т.к. они зависят от конкретного типа используемых детекторов.
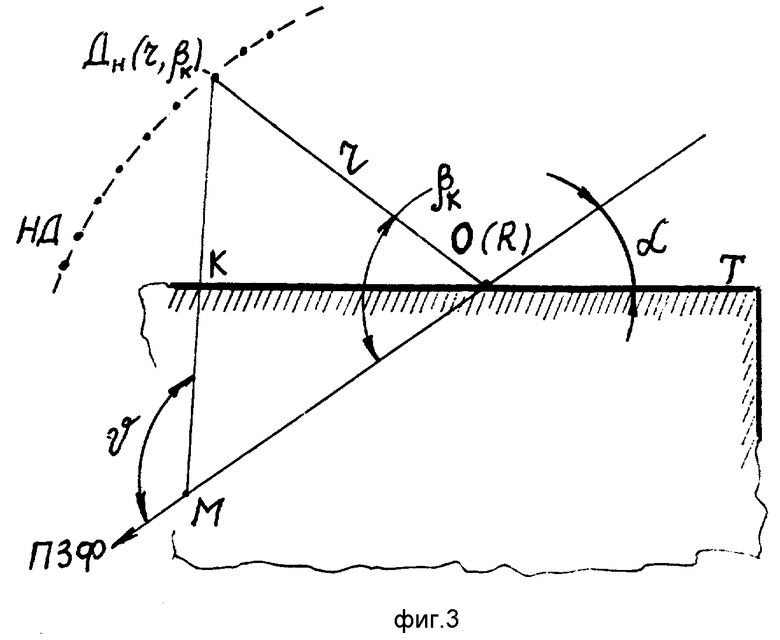
Наиболее эффективно (несмотря на ограничения, связанные с немонохроматичностью зондирующего пучка) применение предлагаемого способа КСЗ в устройстве многодетекторного гамма-локатора [3] с матричной регистрацией рассеянных фотонов [9] поскольку в этом устройстве компактно формируется до ≈ 103 узких, ⊘ ≈ 1 мм, независимых квазиодномерных ПЗФ. Схема стереоскопа на основе [9] фиг. 3, отличается от рассмотренной на фиг. 2 лишь тем, что детекторы рассеянного излучения располагают [10] не на прямой b0=rksin βк, а на дуге окружности r Const с центром в точке O. При этом b0 ≠ Const и угол α ≠ 0. В таком устройстве функция детекторов рассеянного излучения заключается также и в качественном детектировании гамма-локационного сигнала, так что использование спектрометрических детекторов (типа CdTe) полностью избежать не удается, но в то же время достижение эффекта КСЗ не предъявляет дополнительных требований высокого энергетического разрешения к этим детекторам. Поэтому гамма-локатор с матричной регистрацией рассеянных фотонов [3, 9] может обеспечивать двухмерную дефектоскопическую информацию для материалов тяжелее титана (Z 22, a 4,5 г/см3) и стереоскопическую информацию для более легких материалов.
Подписи под рисунками.
Фиг. 1: сравнение схемы оптического стереоскопического зрения (ОСЗ) со схемой однодетекторного комптоновского стереоскопического зондирования (КСЗ):
L положение левого зрачка наблюдателя (или спектрометрического детектора рассеянных фотонов);
R положение правого зрачка наблюдателя (или "глаз Платона" пучок зондирующих фотонов (ПЗФ);
b0 базовое расстояние между точками L и R,
v1, v2 углы комптоновского рассеяния ПЗФ в точках D и C,
w разрешающая сила глаза (радиан), wv2-v1;
B, D равноудаленная от наблюдателя LR различимая пара точек,
A, B неравноудаленная различимая пара точек,
D, C стереоскопически различимая пара точек.
Фиг. 2: схема линейного многодетекторного КСЗ:
T плоскость изучаемого объекта перпендикулярна плоскости рисунка;
O точка внедрения ПЗФ в тело объекта, сопоставима с точкой R на фиг.1;
НД воображаемая линия размещения неспектрометрических детекторов (НД), координаты которых условно отмечены точками;
b0 базовое расстояние;
rk, bк полярные координаты НД;
V угол комптоновского рассеяния;
M точка комптоновского рассеяния;
K точка выхода рассеянного фотона из тела объекта;
Фиг. 3: схема многодетекторного КСЗ с геометрией отдельного ПЗФ в гамма-локаторе [3, 9] Детекторы рассеянных фотонов, расположенные в геометрии полусферы [10] приведены к базовой плоскости, проходящей через ПЗФ перпендикулярно Т. Обозначения см. на фиг.2, базовое расстояние переменно.
Список литературы:
1. Валюс Н. А. // Стереоскопия/. М. Гостехиздат, 1962.
2. Румянцев С. В. Добромыслов В. А. Борисов О. И. // Типовые методики радиационной дефектоскопии и защиты. М. Атомиздат, 1979.
3. Радько В. Е. // Комптоновская гамма-дефектоскопия, ПО ПТЭ, N 4, 1991, с.174 1937.
4. Берестецкий В. Б.Лифшиц Е. М. Питаевский Л.П.// Квантовая электродинамика. М.Наука,1989, с. 404 и 241.
5. Левин Б. Я. // Распределение корней целых функций. М. Гос. изд-во техн.-теор. лит. 1962.
6. Радько В. Е. // Физика и техника измерения комптоновского профиля. ПТЭ, N 2, 1989, с.15 35.
7. Felsteiner J. Pattison P. // Monte Carlo study of Multiple scattering of Photons in Compton NIM, 1975, v. 124, p. 449.
8. М. П. Краснов // Интегральные уравнения. М.Наука, 1975.
9. Радько В. Е. // Устройство для гамма-дефектоскопии, заявка в Госком изобретений N 5028348/25 от 24.2.1992.
10. Радько В. Е. // Комптоновская контрастность в третьем измерении, Комптоновский стереоскоп тезисы к докладу на Международном Совещ. по ядерной спектроскопии и структуре ат. ядра, Минск, 1994, с. 341, 342; Изв. Российской АН, сер. физ. 1994.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО ДЛЯ ГАММА-СТЕРЕОСКОПИИ | 1994 |
|
RU2098800C1 |
| УСТРОЙСТВО ДЛЯ ГАММА-ДЕФЕКТОСКОПИИ | 1992 |
|
RU2080589C1 |
| СПОСОБ КОМПТОН-ФЛЮОРЕСЦЕНТНОГО ЭЛЕМЕНТНОГО АНАЛИЗА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2004 |
|
RU2284028C2 |
| ЗАКРЫТЫЙ РАДИОАКТИВНЫЙ ИСТОЧНИК И СПОСОБ ЕГО ПРИГОТОВЛЕНИЯ | 1995 |
|
RU2098876C1 |
| Гамма-спектрометр | 1975 |
|
SU522651A1 |
| СПОСОБ ГАММА-СПЕКТРОМЕТРИИ | 1997 |
|
RU2159451C2 |
| Гамма-спектрометр | 1975 |
|
SU556651A1 |
| СПОСОБ ГАММА-РАДИОГРАФИЧЕСКОЙ ИНТРОСКОПИИ | 2018 |
|
RU2680849C1 |
| РЕГИСТРАТОР ПРОСТРАНСТВЕННЫХ ПЕРЕМЕЩЕНИЙ | 1992 |
|
RU2077734C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЛОТНОСТИ ТКАНИ ПАТОЛОГИЧЕСКОГО ОЧАГА С ПОМОЩЬЮ ПОЗИТРОННО-ЭМИССИОННОГО ТОМОГРАФА | 2014 |
|
RU2599192C2 |
Сущность изобретения: изобретение позволяет получать информацию о распределении электронной плотности в анализируемом объекте вдоль направления квазиодномерного пучка зондирующих фотонов (ПЗФ). Для этого сначала измеряют распределение интенсивности комптоновски рассеянных фотонов вдоль ПЭФ, а затем решают интегральное уравнение типа уравнения Вольтерра, связывающее распределение интенсивности комптоновски рассеянных фотонов с распределением искомой электронной плотности. В результате использования данного способа вместо двухмерной дефектоскопической информации получают трехмерную информацию. 1 з.п. ф-лы, 3 ил.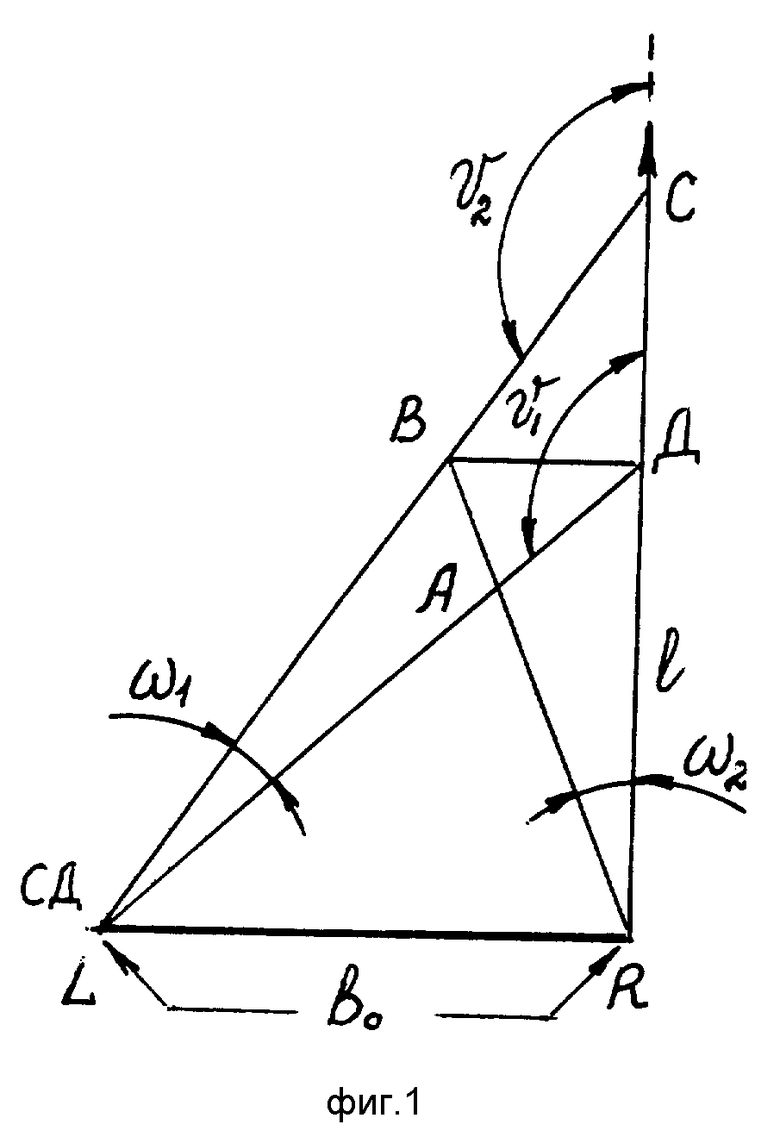
| Румянцев С.В | |||
| и др | |||
| Типовые методики радиационной дефектоскопии и защиты | |||
| - М.: Атомиздат, 1979 | |||
| Радько В.Е | |||
| ПТЭ, N 4, с | |||
| Способ прикрепления барашков к рогулькам мокрых ватеров | 1922 |
|
SU174A1 |
Авторы
Даты
1997-12-10—Публикация
1994-03-10—Подача