Изобретение относится к области специальной радиотехники, а именно к способам восстановления распределения в пространстве волновых случайных неоднородностей среды распространения, меняющихся во времени и пространстве, может быть использовано для неразрушающего контроля объектов (дефектоскопии), в медицинской диагностике (интроскопии), для проведения мониторинга океана, атмосферы и т.п.
Известны методы реконструктивной томографии, позволяющие восстанавливать (определять) количественные характеристики n(r) различных объектов по измеренным интегралам от n(r) по некоторым многообразиям.
Классический способ построения томографических изображений основан на математической операции преобразовании Радона, применяемом в интегральной геометрии. Помимо формулы обращения Радона обратная задача может быть решена другими способами сверточными методами или обратным проектированием с фильтрацией проекций, методами Фурье, алгебраическими процедурами восстановления, матричным методом обращения, итерационными методами и т.д. В общем виде томографические задачи заключаются в восстановлении функции по конечному числу ее линейных интегралов, причем процедура восстановления должна соответствовать схеме сканирования.
Преобразование Радона ставит в соответствие искомой функции f(r) другую функцию:
f′(e,p) = ∫f(r)δ(p-r•e))dr = Re,p{f(r)} (1)
где Re,p{•} преобразование Радона по прямой r•e=p; e - единичный вектор нормали к этой прямой.
Задача заключается в нахождении оператора R-1, такого, что R-1{R{f(r)} R-1{ f'(e, p)} f(r). Оператор R-1 можно выразить в виде последовательности простых операторов, которые могут быть выполнены на цифровых ЭВМ. В качестве примера можно привести Фурье-алгоритм, представляющий собой непосредственную численную реализацию теоремы о проекциях, устанавливающей фундаментальное соотношение между преобразованием Радона, двумерным преобразованием Фурье и оператором, представляющим собой фурье-образ проекции по первой переменной:
где Fr{•} оператор прямого двумерного преобразования Фурье по r=p•e,
Fp{•} оператор прямого одномерного преобразования Фурье по переменной p.
Основу всех методов томографической визуализации составляют три момента: возбуждение, модель взаимодействия со средой и измерения вне объекта.
Методы на базе геометрической оптики предполагают, что наблюденные данные связаны с характеристиками среды n(r) интегралами по прямым линиям (по прямолинейным лучевым траекториям). Модель взаимодействия сводится к преобразованию Радона для неоднородностей вдоль прямолинейных траекторий. Наиболее общая геометрия измерения для двумерной трансмиссионной прямолучевой томографии показана на фиг. 1, из которой видно, что главные допущения метода состоят в следующем:
лучевое (коротковолновое) приближение теории распространения волн, позволяющее не учитывать дифракционные эффекты;
излученная волна проходит к приемнику по прямолинейному пути.
Эти допущения значительно ограничивают общность и соответственно область применения этих методов. Принципы геометрической оптики применимы, когда пространственные размеры отдельных неоднородностей среды много больше длины волны источника излучения (a > λ ), а расстояние, проходимое волной в неоднородной среде, мало по сравнению с первой зоной Френеля (x < a2/l). В ряде областей возможного применения томографических методов, например мониторинг океанических, воздушных сред, количественная визуализация мягких тканей с помощью ультразвука в медицине, ультразвуковая дефектоскопия, радиолокационное картографирование поверхности Земли, восстановление сейсмической информации и т.п. коротковолновое приближение является неадекватным. Несмотря на то, что выражения для реконструкции изображения по прямолинейным траекториям могут быть получены из уравнения Гельмгольца, используемые при выводе приближения оказываются слишком грубыми, что приводит к искажению за счет дифракционных эффектов и рефракции.
Внесение поправок в прямолинейную аппроксимацию траекторий лучей на базе методов геометрической оптики и построение истинного хода лучей (итерационные методы алгебраической реконструкции), как правило, требуют больших затрат машинного времени и для применений, требующих масштаба времени, близкого к реальному, непригодны. Из сравнения результатов реконструкции с использованием допущения о прямолинейном ходе лучей и реконструкции с учетом поправок на искривление (истинных траекторий) лучей можно сделать вывод о том, что хотя учет искривления лучей и устраняет некоторые атрефакты восстановленных изображений, вызванные преломлением, на разрешающую способность они не влияют. Причина здесь в том, что не учитываются дифракционные явления, поскольку в качестве основного уравнения, описывающего распространение, взято уравнение геометрической оптики.
Известны методы восстановления изображений, основанные на дифракционных данных. Дифракционная томография используется в ситуациях, в которых неверны предположения геометрической оптики относительно распространения волн внутри изучаемой среды. Эти методы обычно включают в себя два разных этапа реализации. Первый этап упрощение уравнения модели, позволяющее осуществить его инверсию вычислительно эффективным способом. Второй этап реализации - обработка сигналов, в каком-то смысле обобщение некоторых алгоритмов для недифракционной (прямолучевой) томографии.
В этих методах волновое уравнение, описывающее распространение волн в среде с пространственно изменяющимися волновыми параметрами, решается приближенно. Для скалярного волнового поля, пространственно неоднородной среды и монохроматического возбуждения волновое уравнение может быть сведено к скалярному уравнению Гельмгольца с пространственно переменными коэффициентами:
Δψ(r)+k
где Δ оператор Лапласа, k0 = ω/c0 пространственное волновое число в однородной среде, ω круговая частота, cо скорость распространения в однородной среде, e(r) (cо/с(r))2-1 малое возмущение, 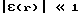 , обусловленное присутствием объекта исследования, c(r) -скорость распространения внутри объекта. Цель решения обратной задачи состоит в том, чтобы получить приближенное изображение ε(r) которое будем называть функцией объекта или сценой, основываясь на данных измерения поля ψ(r) вне объекта.
, обусловленное присутствием объекта исследования, c(r) -скорость распространения внутри объекта. Цель решения обратной задачи состоит в том, чтобы получить приближенное изображение ε(r) которое будем называть функцией объекта или сценой, основываясь на данных измерения поля ψ(r) вне объекта.
Указанные методы используют метод возмущений для преобразования неоднородного волнового уравнения (3) с переменными коэффициентами в неоднородное уравнение с постоянными коэффициентами, которое решается аналитически и учитывает дифракционные эффекты.
Используя условие малости возмущения 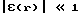 и считая зондирующую волну плоской
и считая зондирующую волну плоской
ψ0(r) = exp(jk•r) (4)
в приближении Рытова уравнение (3) сводится к уравнению
Δu(r)+j2k•▿u(r) = -ε(r). (5)
где u(r) преобразование вида
u(r) = ln[ψ(r)•ψ0(r)] (6)
Будем обозначать заглавной буквой фурье-образ функции, а индексом α у функции указывать, что это функция объекта, повернутого на угол a. Определим оператор поворота A в виде
Пусть Λ = (μ, β) двумерный вектор в частотной области с декартовыми координатами μ и β, а r соответствующий ему вектор в пространственной области с координатами x и y.
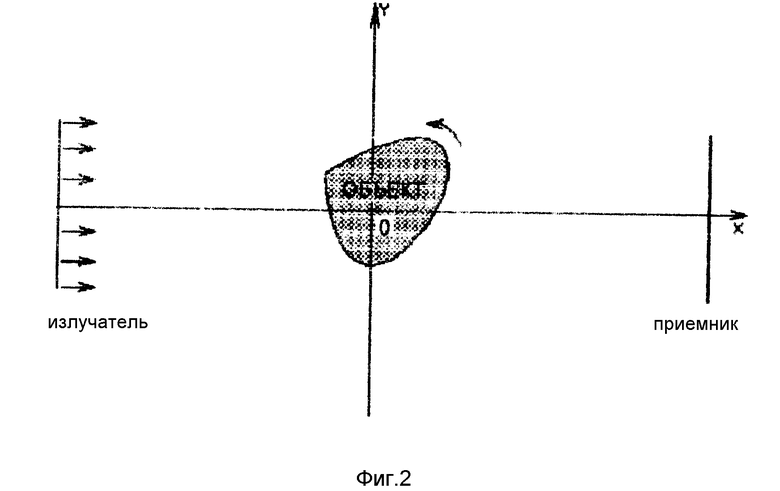
На фиг. 2 показана наиболее общая геометрия измерения для двумерной трансмиссионной дифракционной томографии. Предлагается, что источник возбуждения испускает плоские волны, а матрица приемников измеряет суперпозицию первичного и рассеянного излучения. База данных для осуществления инверсии получается в результате когерентного измерения рассеянных волн для некоторого числа угловых ориентаций объекта.
Для объекта, повернутого на угол a, измеряется поле j0(x0, y) и преобразуется в функцию uα(x0, y) (6). Одномерный фурье-образ функции uα(x0, y) по координате y связан с пространственным спектром сцены e(r) следующим образом: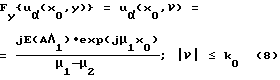
где Fy{•} оператор одномерного преобразования фурье по координате y;
E(AΛ1) = Fr{εα(r)} = Fr{ε(Ar)} пространственный спектр сцены;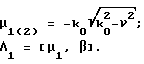
Обратно,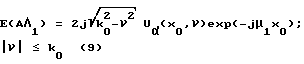
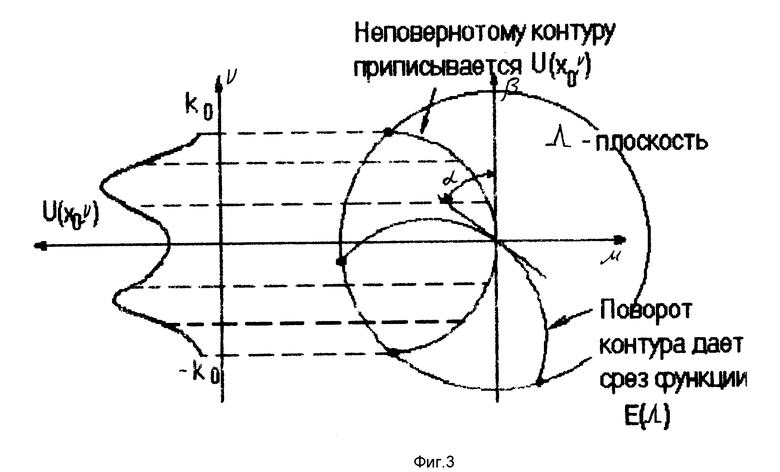
Соотношение (9) устанавливает связь в фурье-области между одномерным фурье-образом преобразованного измеренного поля и двумерным фурье-образом восстанавливаемой сцены (функции объекта ε(r)). Так как величина ν переменная, вектор 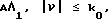 описывает в фурье-пространстве ([μ, β] плоскости) полукруглый контур, на котором функция E(·) может быть определена по функции Uα(x0, ν). На фиг.3 показаны контур для данного угла α и процесс, с помощью которого значения функции Uα(x0, ν) отображаются на этот контур, чтобы получить приближенное полукруглое "сечение" функции E(Λ). Набор данных для реконструкции сцены ε(r) осуществляется путем плотного покрытия частотной плоскости этими дифракционными сечениями при варьировании угла α. На основе этой базы данных сцена может быть восстановлена с помощью алгоритмов известных из прямолучевой томографии: в фурье-области и в пространственной области. В частности, реконструкция в фурье-области включает в себя интерполяцию дискретных данных с полукруглых контуров реконструкции на однородную прямоугольную сетку в частотной области и применение быстрого преобразования Фурье (БПФ).
описывает в фурье-пространстве ([μ, β] плоскости) полукруглый контур, на котором функция E(·) может быть определена по функции Uα(x0, ν). На фиг.3 показаны контур для данного угла α и процесс, с помощью которого значения функции Uα(x0, ν) отображаются на этот контур, чтобы получить приближенное полукруглое "сечение" функции E(Λ). Набор данных для реконструкции сцены ε(r) осуществляется путем плотного покрытия частотной плоскости этими дифракционными сечениями при варьировании угла α. На основе этой базы данных сцена может быть восстановлена с помощью алгоритмов известных из прямолучевой томографии: в фурье-области и в пространственной области. В частности, реконструкция в фурье-области включает в себя интерполяцию дискретных данных с полукруглых контуров реконструкции на однородную прямоугольную сетку в частотной области и применение быстрого преобразования Фурье (БПФ).
Наиболее близким к предлагаемому изобретению является способ восстановления пространственных неоднородностей среды распространения волн, состоящий в определении количественных характеристик таких неоднородностей внутри исследуемого объекта на основании наблюдений рассеянного объектом поля и использования алгоритма реконструкции в фурье-области. В этом методе может быть выделена следующая последовательность операций:
1) излучение источником возбуждения непрерывной плоской волны (4), направленной на исследуемый объект;
2) когерентное измерение линейной матрицей приемников с равномерным пространственным периодом дискретизации рассеянного поля jα(x0,y);
3) поворот исследуемого объекта относительно его геометрического центра на некоторое число фиксированных углов α и повторение операций, описанных в пунктах 1) и 2) для каждой угловой ориентации объекта;
4) преобразование (6) измеренного поля jα(x0,y) в функцию Uα(x0,ν);
5) одномерное БПФ функции Uα(x0,y) по координате y для всех углов измерений α;
6) получение дискретных значений двумерного пространственного спектра сцены E(Λ) на основе набора одномерных спектров Uα(x0,ν) в соответствии с выражением (9);
7) интерполяция нерегулярно расположенных на дискретной сетке частот спектральных компонент E(Λ) на равномерную сетку;
8) обратное двумерное БПФ пространственного спектра сцены E(Λ), восстанавливающее функцию объекта ε(r).
Недостаток данного способа состоит в том, что реконструируемые рассеиватели предполагаются детерминированными и "замороженными", т.е. обладающими неизменными характеристиками в течение времени измерения (лоцирования).
Вместе с тем в ряде практических ситуаций, например в медицине при визуализации кровотока в тканях и сосудах, томографии структур, совершающих быстрые движения (например, сердце человека, которое сокращается примерно раз в секунду), а также в гидро- и атмосферной акустике, когда времена флуктуации неоднородностей сравнимы с длительностью зондирующего сигнала, такое предположение является слишком грубым. В этом случае для гармонических полей происходят случайные доплеровские смещения несущей частоты, приводящие к существенному уширению спектра рассеянного поля, а для широкополосных зондирующих сигналов происходит рассогласование рассеянного сигнала с излучением. Это приводит к появлению артефактов восстановленных изображений (функций объекта) в случае медленных по сравнению с длительностью зондирующего сигнала флуктуаций и к невозможности восстановления сцены в случае быстрых флуктуаций.
Целью изобретения является расширение способов восстановления пространственного распределения неоднородностей на неоднородности, изменяющиеся во времени.
Поставленная задача достигается тем, что в способах реконструктивной томографии проекции исследуемого объекта предлагается формировать особым образом, а именно облучением объекта одновременно с противоположных направлений для различных проекционных углов, создавая в исследуемом объекте поле, представляющее собой суперпозицию плоских волн, распространяющихся попарно навстречу друг другу, измерением рассеянных в направлениях облучения объектом сигналов и вычислением корреляционной функции комплексных огибающих рассеянных сигналов, измеренных с противоположных направлений.
Предложенная схема облучения объекта и измерения рассеянного сигнала построена на основе модели взаимодействия плоской монохроматической волны с изменяющимися во времени неоднородностями в рамках теории метода плавных возмущений (метода Рытова).
Распространение волн в средах с флуктуирующими во времени и пространстве параметрами в скалярном случае описывается дифференциальным уравнением вида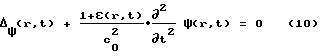
где ε(r,t) (cо/с(r, t))2-1 случайные флуктуации квадрата показателя преломления скорости звука в рассеивающем объеме.
Вводя новую функцию
u = lnψ (11)
и рассматривая ε(r,t) как малое возмущение 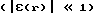 , найдем решение уравнения (10), подставив в него функцию u (11), методом малых возмущений.
, найдем решение уравнения (10), подставив в него функцию u (11), методом малых возмущений.
Поместим начало координат в центре рассеивающей области М (заполненной неоднородностями коэффициента преломления). Возьмем в качестве нулевого приближения функцию u, соответствующую плоской монохроматической волне, распространяющейся вдоль оси X:
u0 = lnA0-j(ω0t-k0x) (12)
Известно, что в первом приближении метода плавных возмущений решение уравнения (10) для функции (11) имеет вид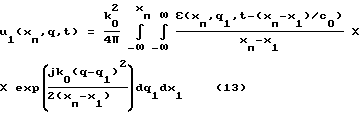
где rп=(xп,q) точка размещения приемника.
Это уравнение получено в предположении, что размеры неоднородностей значительно больше длины падающей волны λ0 = 2π/k0, а характерный период их изменения во времени значительно больше периода падающей волны T0 = 2π/ω0.
Рассмотрим случай, когда точка наблюдения отодвинута от объема, занятого неоднородностями, в область фраунгоферовой дифракции:
xпλ ≫ L2 (14)
где L максимальный диаметр рассеивающей области. В этом случае в знаменателе (13) можно положить
xп-x1≈xп, (15)
а
exp(jπa2/λxп) ≈ 1. (16)
Тогда с учетом конечности в пространстве рассеивающей области М (13) перепишется
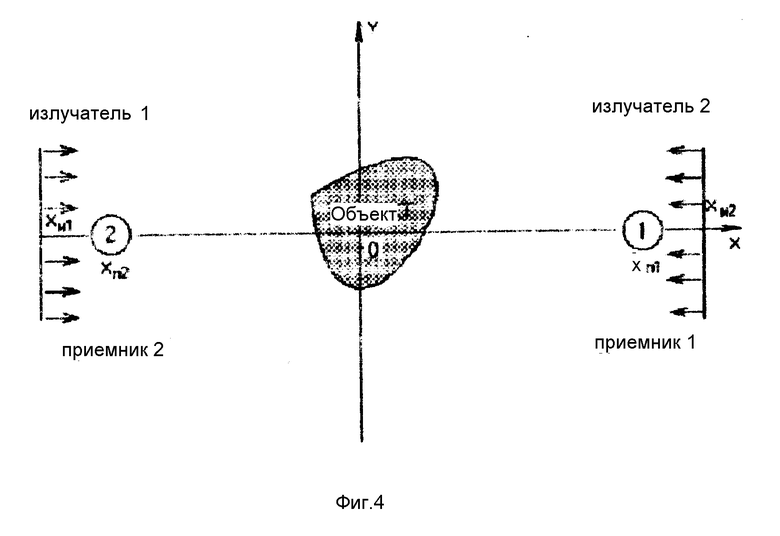
Зондирующую плоскую волну ψ0 expuо в рассеивающей области будем создавать источником, расположенным в точке rи1 (-xи,q) фиг. 4, где xи>xп):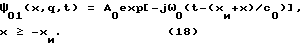
Тогда поле в точке rп1=(xп,q) на основании (11) запишется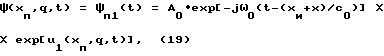
а логарифм комплексной огибающей сигнала ψп1(t), обозначим его vп1(t), запишется в виде
vп1(t) u1(xп,q,t) + jkо(xи+xп) + lnAо, (20)
Если изменить расположение источника и приемника относительно центра сцены на противоположное, т.е. для первичной волны, создаваемой источником, расположенным в точке rи2=(xи,q),
ψ02(x,q,t) = A0exp[-jω0(t-(xи-x)/c0)], (21)
логарифм комплексной огибающей поля ψ(rп2,t) = ψп2(t) в точке rп2=(-xп, q) фиг.4 по аналогии с (19) и (20) имеет вид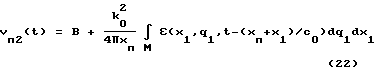
где B=jkо(xи+xп) + lnAо. (23)
Найдем функцию ковариации сигналов vп1(t) и vп2(t) на основании (17), (20) и (22), полагая, что среда в среднем однородна, то есть <ε(r,t)>=0: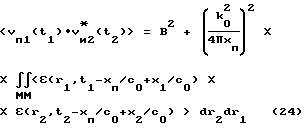
Положим, что неоднородности среды имеют ковариационную функцию вида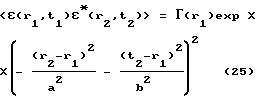
где a много меньше элемента разрешения томографической системы d, но много больше длины падающей волны λ0, а b много меньше величины d/cо, но много больше периода зондирующего сигнала T0 = λ0/c0. В этом случае ковариационную функцию (25) можно приближенно записать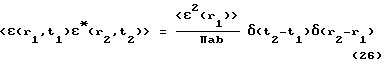
Множители 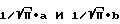 появляются вследствие того, что площадь под функцией, стремящейся к δ-функции, должна быть равна единице.
появляются вследствие того, что площадь под функцией, стремящейся к δ-функции, должна быть равна единице.
Тогда корреляционная функция сигналов vп1(t) и vп2(t)
Для двумерного случая r (x, y) (27) можно переписать
<vп1(t)•v
где 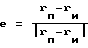 единичный вектор в направлении с источника на приемник.
единичный вектор в направлении с источника на приемник.
Таким образом, корреляционная функция двух сигналов vп1(t) и vп2(t) с точностью до констант равна преобразованию Радона по прямой r•e = cτ/2, т.е. проекции среднего квадрата сцены <ε2(r)> на направление единичного вектора e. При наличии таких проекций для различных направлений сцена может быть визуализирована стандартными алгоритмами восстановления, используемыми в томографии. В частности, при использовании методов Фурье, основанных на соотношении (2), необходимо выполнить последовательность одномерных преобразований Фурье корреляционных функций (28) по переменной p = cτ/2 для различных направлений e (проекционных углов α), что позволит получить значения двумерного спектра функции <ε2(r)> на полярной сетке пространственных частот. Обратное двумерное преобразование Фурье от этих значений даст саму функцию <ε2(r)>.
Набор данных, достаточный для реконструкции функции <ε2(r)>, предлагается получать с помощью набора систем излучателей и приемников, аналогичных описанной выше фиг.4, для различных направлений e (проекционных углов α).
В предлагаемом способе реконструкции пространственного распределения меняющихся во времени случайных волновых неоднородностей среды может быть выделена следующая последовательность операций:
1) излучение набором из N систем излучателей, расположенных вокруг исследуемого объекта с угловым шагом Da, каждая из которых (систем) состоит из двух излучателей, расположенных симметрично относительно геометрического центра исследуемого объекта в точках rиi1 и rиi2, причем rиi1=-rиi2=rи•eиi1= -rи•eиi2, где rи= 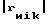 , eиik=rиik/rи, k 1, 2, плоских монохроматических волн
, eиik=rиik/rи, k 1, 2, плоских монохроматических волн
создающих в исследуемом объекте поле, представляющее собой суперпозицию плоских волн, распространяющихся попарно (ψ0i1(r,t) и ψ0i2(r,t)) навстречу друг другу;
когерентное измерение системой ненаправленных приемников, расположенных вокруг исследуемого объекта в дальней зоне относительно него в точках rпik, причем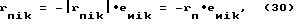
суперпозиции первичного и рассеянного излучения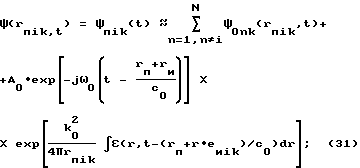
3) выделение комплексных огибающих ψпik(t) измеренных сигналов ψпik(t) для i=1, N, k 1, 2: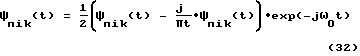
4) преобразование (12) комплексных огибающих ψпik(t) в функцию vпik(t):
vпik(t) = ln[ψпik(t) i=1, ..., N, k = 1,2; (33)
5) удаление постоянных составляющих сигналов vпik(t):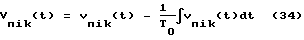
где i=1,N, k=1, 2; Tо длительность зондирующего сигнала;
6) вычисление корреляционных функций
hi(τ) = <VПi1(t)•V
для i=1,N;
7) одномерные преобразования Фурье функций hi(τ) для i=1,N, т.е. для всех углов измерений αi:
Hi(ν) = F{hi(τ)}; (36)
8) формирование дискретных по углу значений двумерного пространственного спектра сцены E(k) = Fr{<ε2(r)>} на основе набора одномерных спектров
9) обратное двумерное преобразование Фурье пространственного спектра сцены E(k), восстанавливающее функцию объекта <ε2(r)>.
Следует отметить, что при использовании процедуры быстрого преобразования Фурье (БПФ) после выполнения последовательности одномерных БПФ необходимо произвести интерполяцию значений двумерного спектра функции <ε2(r)> с полярной на прямоугольную сетку частот.
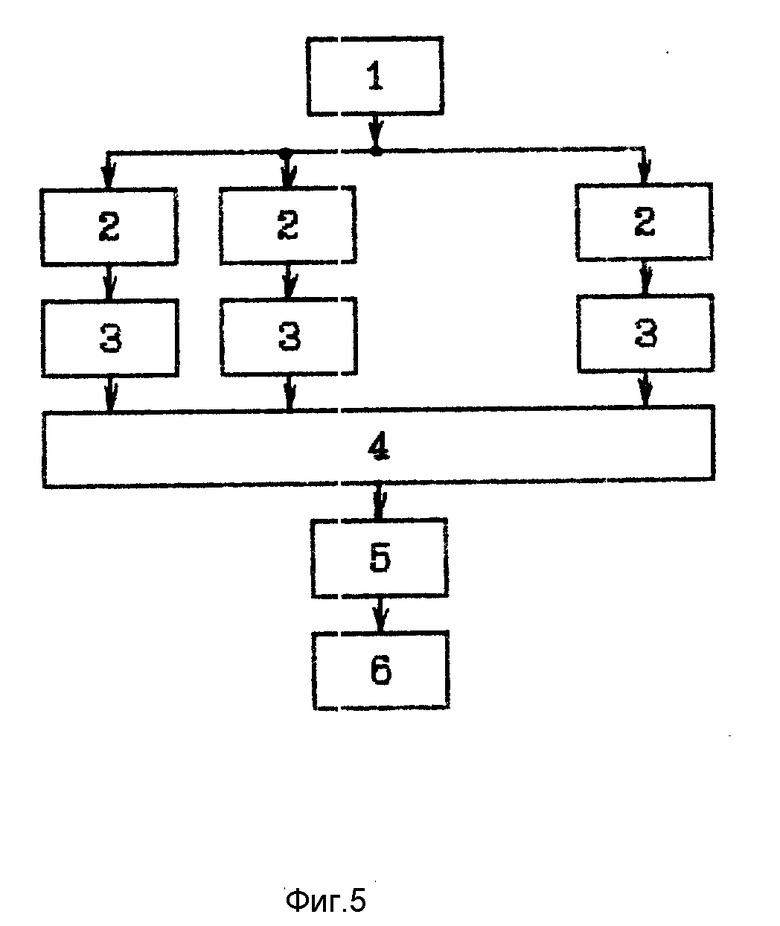
Предлагаемый способ восстановления пространственного распределения меняющихся во времени случайных волновых неоднородностей среды может быть реализован с помощью устройства представленного на фиг.5, которое состоит из генератора 1 тонального сигнала, N блоков 2 формирования проекций исследуемого объекта, N блоков 3 вычисления одномерного быстрого преобразования Фурье (БПФ), блока 4 вычисления двумерного дискретного спектра на основе N одномерных, интерполятора 5, блока 6 вычисления обратного двумерного БПФ.
С блока 1 тональный сигнал поступает на входы всех блоков 2, в каждом из которых формируется проекция исследуемого объекта hi(m) для соответствующего направления (функциональная схема блока описана ниже). С выходов блоков 2 проекции hi(m) поступают на блоки 3, в которых вычисляются одномерные БПФ проекций Hi(n) в соответствии с (36), которые затем поступают на N входов блока 4, в котором формируется двумерный спектр E(k) на основе набора одномерных спектров Hi(n) в соответствии с (36). С выхода блока 4 дискретные значения спектра E(k) поступают в блок 5, в котором производится интерполяция двумерного спектра функции E(k) с полярной сетки пространственных частот на прямоугольную. После интерполяции в блоке 5 спектр E(k) поступает на блок 6, в котором производится обратное двумерное БПФ спектра E(k) и тем самым восстанавливается функция объекта <ε2(r)>.
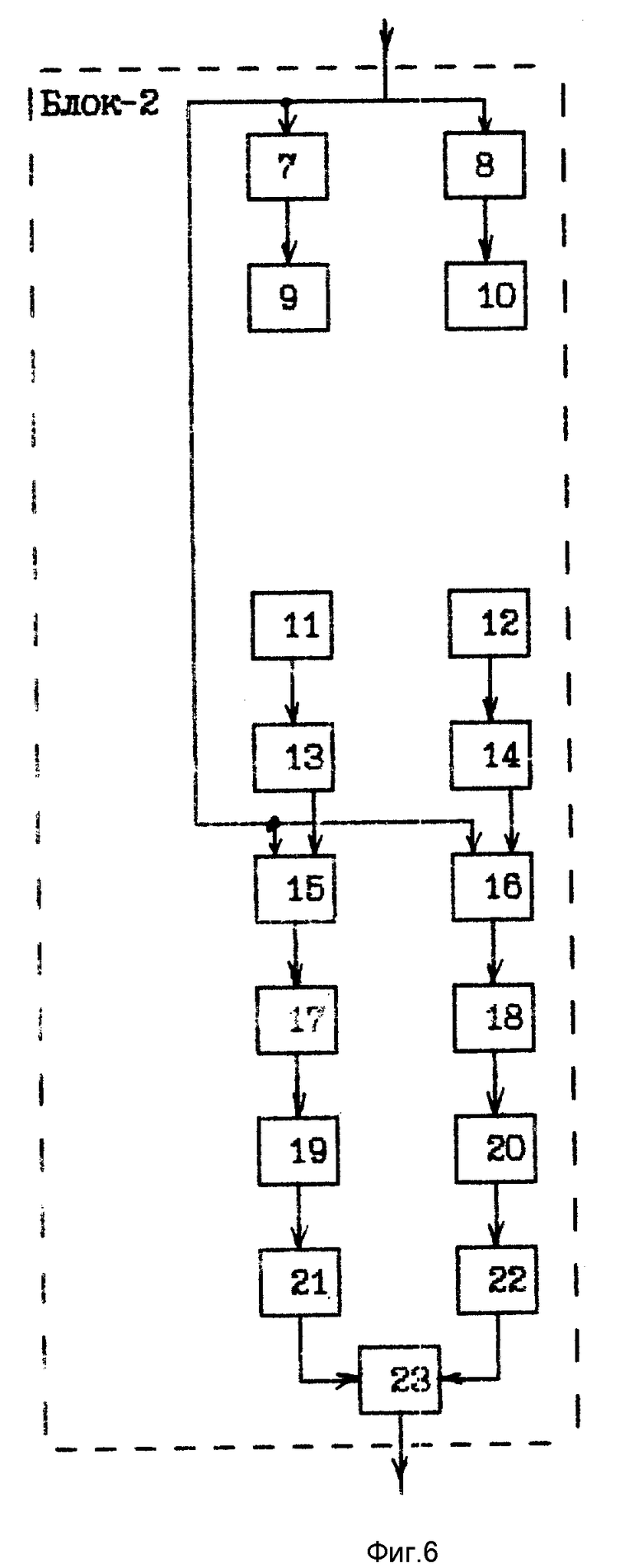
Функциональная схема блока формирования проекции исследуемого объекта для одного направления (блока 2) представлена на фиг. 6, где 7 усилитель 1, 8 усилитель 2, 9 излучатель 1 (плоских волн), 10 излучатель 2 (плоских волн), 11 приемник 1 (ненаправленный), 12 приемник 2 (ненаправленный), 13 предварительный усилитель 1, 14 предварительный усилитель 2, 15 - синхронный детектор 1, 16 синхронный детектор 2, 17 аналого-цифровой преобразователь 1 (АЦП 1), 18 аналого-цифровой преобразователь 2 (АЦП 2), 19 блок вычисления логарифма 1, 20 блок вычисления логарифма 2, 21 блок удаления постоянной составляющей 1, 22 блок удаления постоянной составляющей 2, 23 коррелятор.
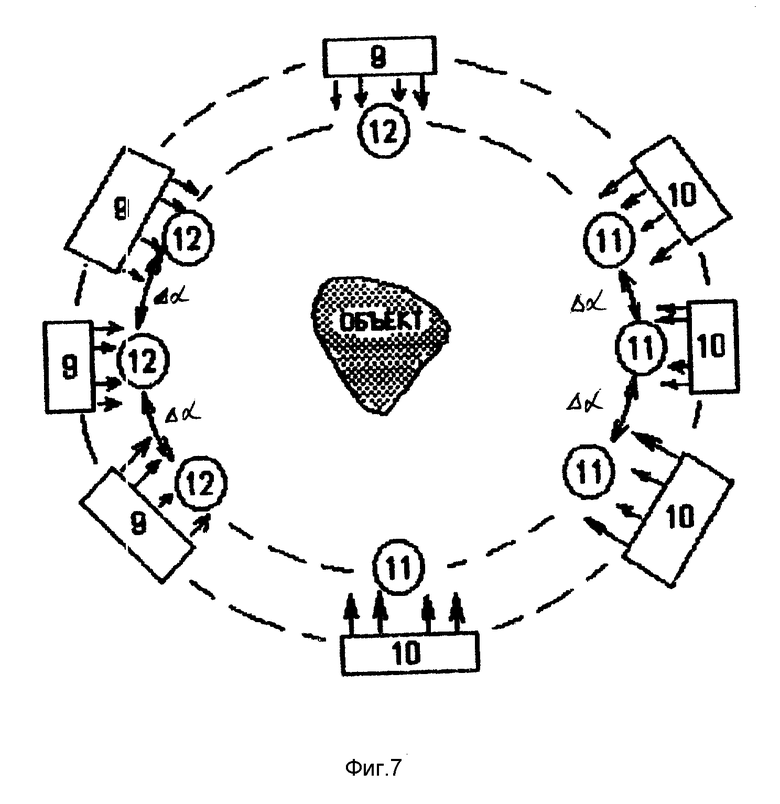
Блоки 7, 9, 11, 13, 15, 17, 19, 21 образуют канал измерения 1, а блоки 8, 10, 12, 14, 16, 18, 20, 22 канал измерения 2. Принцип работы блока 2 заключается в следующем. Тональный сигнал с входа блока 2 поступает на усилители (7, 8) и синхронные детекторы (15, 16) каналов 1 и 2. Усиленные тональные сигналы с выходов блоков 7, 8 подаются на соответствующие излучатели (блоки 9, 10). Излучатель 1 и приемник 1 (9, 11) расположены на прямой, проходящей через геометрический центр исследуемого объекта по разные стороны относительно него, причем приемник 1 (11) расположен в дальней зоне относительно объекта в соответствии с выражением (33), а излучатель 1 (9) на расстоянии от центра объекта большем, чем приемник 1 (11). Излучатель 2 и приемник 2 (10, 12) расположены симметрично излучателю 1 и приемнику 1 (9, 11) соответственно относительно геометрического центра исследуемого объекта. Схема размещения излучателей 1, 2 и приемников 1, 2 блока 2 (9, 10, 11, 12) представлена на фиг. 7. Излучатели 1, 2 создают в исследуемом объекте две плоские монохроматические волны, распространяющиеся навстречу друг другу.
Излучатели и приемники всех N блоков 2 расположены вокруг исследуемого объекта с угловым шагом Δα 180o/N фиг.7 для формирования проекций исследуемого объекта для всевозможных направлений. Таким образом, в исследуемом объекте создается поле, представляющее собой суперпозицию плоских волн, распространяющихся попарно навстречу друг другу в соответствии с выражением (29), где k 1 соответствует излучателю 1 (9), k 2 излучателю 2 (10), а индекс i 1,N номеру блока 2.
Приемники 1, 2 (11, 12) измеряют суперпозицию первичного и рассеянного излучения в соответствии с выражением (31). С выхода приемников 1, 2 (11, 12) измеренные реализации jпi1(t), ψпi2(t) через предварительные усилители 1, 2 (13, 14) поступают на первые входы синхронных детекторов 1, 2 (15, 16), на вторые входы которых поступает опорный тональный сигнал с генератора (1). В синхронных детекторах 1, 2 (15, 16) выделяются комплексные огибающие ψпi1(t) и ψпi2(t) измеренных сигналов ψпi1(t) и ψпi2(t) в соответствии с выражением (32). С выходов блоков 15, 16 комплексные огибающие подаются на входы АЦП 1, 2 (17, 18) соответственно, в которых производится дискретизация и квантование с частотой дискретизации, удовлетворяющей условиям теоремы Котельникова для комплексных огибающих ψпi1(t) и ψпi2(t). С выходов блоков 17, 18 дискретные квантованные выборки ψпi1(t) и ψпi2(t) поступают на входы соответственно блоков 19, 20, в которых вычисляются логарифмы vпi1(m) и vпi2(m) этих выборок в соответствии с (33). С выходов блоков 19, 20 результаты подаются на входы блоков 21, 22 соответственно, в которых реализации центрируются в соответствии с выражением (34). С выходов блоков 21, 22 центрированные реализации Vпi1(m) и Vпi2(m) поступают на соответствующие входы коррелятора (23), в котором вычисляется их корреляционная функция в соответствии с выражением (35). Таким образом, на выходе коррелятора (23), который является выходом блока 2, формируется проекция hi(m) среднего квадрата сцены <ε2(r)> на направление, определяемое прямой, на которой размещены излучатели 1, 2 (9, 10) и приемники 1, 2 (11, 12) данного (i-го) блока 2.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ АКУСТИЧЕСКОГО ПРЕДСТАВЛЕНИЯ ПРОСТРАНСТВЕННОЙ ИНФОРМАЦИИ ДЛЯ ИНВАЛИДОВ ПО ЗРЕНИЮ | 1993 |
|
RU2085162C1 |
| СПОСОБ КОРРЕЛЯЦИОННОЙ ОБРАБОТКИ СИГНАЛОВ, ОТРАЖЕННЫХ ОТ БЫСТРОДВИЖУЩИХСЯ ЦЕЛЕЙ | 2005 |
|
RU2293997C1 |
| УСТРОЙСТВО ДЛЯ ПРИЕМА РЕЧЕВЫХ СИГНАЛОВ | 1993 |
|
RU2049426C1 |
| ШИРОКОПОЛОСНЫЙ ИМПУЛЬСНЫЙ ИЗЛУЧАТЕЛЬ НАПРАВЛЕННОГО ДЕЙСТВИЯ | 1995 |
|
RU2099831C1 |
| СПОСОБ ПОЛУЧЕНИЯ СЕЙСМИЧЕСКОГО РАЗРЕЗА | 1991 |
|
RU2022310C1 |
| СПОСОБ И УСТРОЙСТВО ОБНАРУЖЕНИЯ СЛОЖНЫХ ШИРОКОПОЛОСНЫХ ЧАСТОТНО-МОДУЛИРОВАННЫХ СИГНАЛОВ С ФИЛЬТРАЦИЕЙ В МАСШТАБНО-ВРЕМЕННОЙ ОБЛАСТИ | 2004 |
|
RU2282209C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ СЛОЖНЫХ ШИРОКОПОЛОСНЫХ ЧАСТОТНО-МОДУЛИРОВАННЫХ СИГНАЛОВ С ФИЛЬТРАЦИЕЙ В МАСШТАБНО-ВРЕМЕННОЙ ОБЛАСТИ НА ОСНОВЕ ДИСКРЕТНОГО ВЕЙВЛЕТ-ПРЕОБРАЗОВАНИЯ | 2010 |
|
RU2439601C1 |
| СПОСОБ ПЕРЕДАЧИ РЕЧЕВЫХ СИГНАЛОВ | 1993 |
|
RU2049456C1 |
| СПОСОБ ВОССТАНОВЛЕНИЯ РЕЛЬЕФА МОРСКОГО ДНА ПРИ ИЗМЕРЕНИЯХ ГЛУБИН ПОСРЕДСТВОМ ГИДРОАКУСТИЧЕСКИХ СРЕДСТВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2010 |
|
RU2429507C1 |
| СПОСОБ АКУСТИЧЕСКОГО ПРЕДСТАВЛЕНИЯ ПРОСТРАНСТВЕННОЙ ИНФОРМАЦИИ ДЛЯ ПОЛЬЗОВАТЕЛЕЙ | 2012 |
|
RU2523340C2 |
Изобретение относится к области специальной радиотехники, а именно к способам восстановления распределения в пространстве волновых случайных неоднородностей среды распространения, меняющихся во времени и пространстве, может быть использовано для проведения мониторинга океана и атмосферы, в медицине при визуализации динамических структур, для неразрушающего контроля объектов (дефектоскопии) и т. п. Отличительной особенностью предлагаемого способа является то, что проекции динамического объекта предлагается получать путем одновременного облучения объекта с противоположных относительно его центра направлений и вычисления корреляционной функции сигналов, прошедших через объект. Восстановление пространственного распределения неоднородностей производится стандартными методами реконструктивной томографии на основе набора проекций объекта, полученных указанным выше способом, для различных проекционных углов. 7 ил.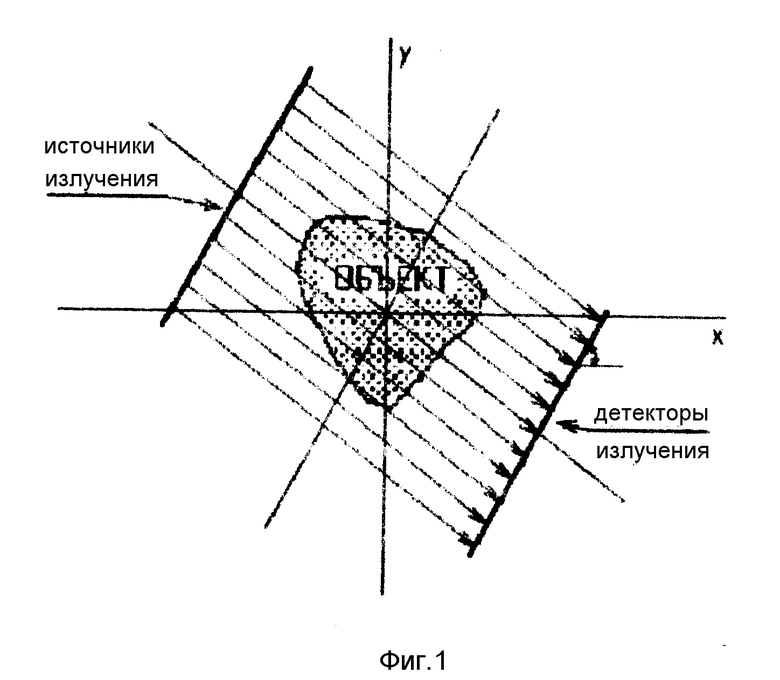
Способ восстановления пространственного распределения случайных волновых неоднородностей среды, меняющихся во времени, основанный на операциях облучения объекта с различных направлений монохроматическими волнами, измерения рассеянных объектом сигналов на различные направления, вычисления прямого одномерного преобразования Фурье проекций сцены на различные направления, обратного двумерного преобразования Фурье пространственного спектра сцены, отличающийся тем, что дополнительно проводят операции облучения объекта попарно на линиях, проходящих через геометрический центр объекта и соответствующих разным проекционным углам, причем в каждой паре облучение производят одновременно, создавая в исследуемом объекте поле, представляющее собой суперпозицию плоских волн, распространяющихся попарно одна навстречу другой, измерения рассеянных в направлениях облучения объектом сигналов, вычисления корреляционной функции комплексных огибающих рассеянных сигналов, измеренных с противоположных направлений.
| Реконструкция изображений / Под ред | |||
| Старка Г | |||
| - М.: Мир, 1992, с.441 - 491. |
Авторы
Даты
1997-12-20—Публикация
1995-07-26—Подача