Изобретение относится к области инженерной геологии и геофизики.
Цель изучения деформационных свойств - определение количественных характеристик: модулей упругости, деформации, коэффициента Пуассона и т.п., отображающих деформируемость изучаемых тел при заданных условиях силовых воздействий и необходимых для расчетов напряженно-деформируемого состояния.
Основные показатели деформируемости обычно определяются в результате статических нагружений горных пород в отдельных наиболее характерных точках (участках) исследуемого массива.
Основными статическими методами определения деформационных характеристик горных пород в натурных условиях являются, м3:
Метод штампа, объем деформируемой зоны - 0,5 - 2,0
Метод гидравлических подушек, объем деформируемой зоны - 10
Метод гидростатической камеры, объем деформируемой зоне - 102 - 104
Метод радиального пресса, объем деформируемой зоны - 10 - 102
Метод скважинных дилатометров и прессиометров, объем деформируемой зоны - 0,01 - 1,0
Известен метод прессиометрических испытаний, заключающийся в том, что в скважину опускают каротажный зонд, представляющий собой замкнутый сосуд, внутреннее давление жидкости в котором передается на стенки определенного участка длины скважины. Смещения стенок скважины, возникающие в результате этого, могут быть измерены и, с учетом некоторых идеализирующих предпосылок, позволяют составить определенное представление о деформируемости скального массива в зоне загруженного участка скважины, см. Витке В. Механика скальных пород.-М.: Недра, 1990.
Для исследования деформируемости породы при нагружении и разгрузке, как правило, применяются программу нагружения, предусматривающую несколько циклов нагружения и разгрузки в течение времени t. В каждом цикле нагружения давление повышают ступенями до конечного значения, увеличивающегося в каждом последующем цикле. При принятии максимального давления стремятся к тому, чтобы оно соответствовало нагрузкам на породу, ожидаемым в ходе строительства, а также за тем, чтобы в скважине не создавались большие необратимые деформации, в результате которых при испытаниях получают слишком низкие значения модуля деформации. В каждом цикле разгрузки давление понижают также ступенями, до тех пор пока оно не достигнет начального значения P0. Отсчеты измеряемых величин продолжают до тех пор, пока смещение стенок скважины не достигнет конечного значения.
Нанеся на график нагрузки P соответствующие им изменения диаметра скважины Δd (или ΔV изменение объема рабочей камеры), получают зависимости перемещения стенок скважины от давления. Модули деформации Ee и упругости Ew определяются из выражения
EE= c·ΔP/ΔdE; EW= c·ΔP/ΔdW; EW≥EE
где
C - константа, зависящая от применения конструкции зонда,
ΔdE и ΔdW - изменение диаметра скважины при первичном нагружении и разгрузке. Для измерения перемещений используются индуктивные датчики перемещений.
Основные недостатки аналога заключаются в следующем:
1. Ограничены возможности применения дилатометров, так как необходим выбор участка измерений, т.е., например, наличие дефектов различного типа может исказить условия нагружения или сделать его невозможным. Для предварительной оценки и выбора испытательных участков скважины следует использовать керн и, при возможности, провести телевизионное обследование скважин.
2. Передающиеся на стенку скважины напряжения быстро затухают по мере удаления вглубь массива, поэтому объем скальной породы, исследуемый в прессиометрических испытаниях не всегда представителен (для дилатометров системы LNEC объем составляет около 0,06 м3).
3. Значительный разброс результатов прессиометрических испытаний, обусловленный методикой испытаний, вызывает необходимость проведения большого числа испытаний, чтобы более или менее надежно судить о распределении модулей деформации. Представительным для деформируемости исследуемого массива является лишь среднее геометрическое значение 
4. Большая трудоемкость и высокая стоимость исследований.
Все известные статические методы изучений искомых параметров охватывают малый объем изучаемого тела, остается неизвестной картина распределения их по объему массива. Для исключения этого фактора производится оценка деформационных характеристик с применением методик сейсмоакустических исследований. При применении известных геофизических методов существуют существенные различия деформационных характеристик, полученных разными методами - статическими и динамическими.
Известен способ нахождения модуля упругости по данным ультразвукового каротажа (Савич А. И. и др. Сейсмоакустические методы изучения массивов скальных пород. -М.: Недра, 1969, с. 155-166). В данном методе производится ультразвуковой каротаж скважин с получением многоканальных встречных осциллограмм. Обработка осциллограмм осуществляется в следующем порядке:
а) производится выделение и корреляция выбранных фаз основных P и R волн на осциллограммах УЗК;
б) снимаются времена прихода выделенных фаз колебаний;
в) вычисляются средние приращения времен прихода волн двух встречных наблюдений на исследуемой базе (шаг зонда);
г) вычисляют скорости волн VP и VR по полученным значениям времен;
д) рассчитывают отношение скоростей выделенных волн VR/VP;
е) находим величину отношений длины волны LR к периметру скважины 2πr0, где r0 - радиус исследуемой скважины;
ж) с помощью номограммы Кнопова-Коптева по отношению величин скоростей VR/VP с учетом величины LR/2πr0 находят коэффициент Пуассона - ν.
з) динамический модуль упругости Eдин по скважине вычисляют по значениям скорости продольной волны VP и коэффициенту Пуассона с помощью выражения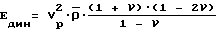
где - среднее значение плотности, соответствующее нетрещиноватым породам (образцам).
- среднее значение плотности, соответствующее нетрещиноватым породам (образцам).
Данное техническое решение выбрано в качестве прототипа, так как в нем, так же как и в предлагаемом методе, осуществляется ультразвуковой каротаж исследуемой скважины, нахождение и расчет скоростей двух типов волн, анализ типов волн, нахождение величин коэффициента Пуассона и модуля упругости.
Недостатками прототипа являются:
1. Значительное различие модулей упругости, полученных разными способами - статическими и динамическими.
2. Невозможность оценки модуля деформации.
3. Невозможность полной и достоверной оценки трещиноватости исследуемого тела из-за искажения искомых параметров напряженным состоянием и неучета направленности параметра - скорость величина векторная. Невозможность оценки объемной трещиноватости и ее параметров в двух взаимно перпендикулярных направлениях.
Целью изобретения являются масштабная оценка статического модуля упругости Eст и модуля деформации D, оценка трещиноватости, не искаженной присутствующим в сооружении, массиве напряженным состоянием, и ее изменение под действующей нагрузкой.
Согласно изобретению способ определения состояния и деформационных параметров тела, сооружения, массива, включающий проведение наблюдений с помощью ультразвукового каротажа скважины на многоканальным встречным осциллограммам упругих волн двух типов P и R т отношения их скоростей VR/VP, оценку отношения длины волны LR к периметру скважины 2πr0 и по величине отношения скоростей с учетом величины LR/2πr0 по дополненной номограмме Кнопова-Коптева нахождение коэффициента Пуассона ν и динамического модуля упругости, характеризуется тем, что рассчитывают величину конечного параметра формы порового пространства Aк для нагрузки, испытываемой сооружением в данной точке в момент проведения УЗК по выражению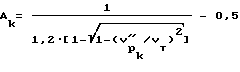
где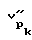 - скорость продольной волны вдоль оси скважины для нагрузки, испытываемой телом в данной точке,
- скорость продольной волны вдоль оси скважины для нагрузки, испытываемой телом в данной точке,
Vт - скорость продольной волны в скелете материала.
Затем решают уравнение третьей степени вида A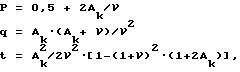
после чего рассчитывают величины скоростей продольной волны для напряженного состояния в рассматриваемой точке тела перпендикулярно оси скважины 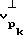 по выражению
по выражению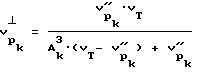
для разгруженного состояния вдоль оси скважины 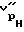 и перпендикулярно оси скважины
и перпендикулярно оси скважины 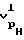 по выражениям
по выражениям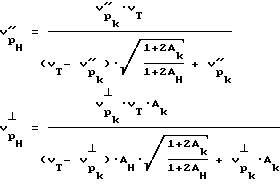
Затем по величинам скоростей продольной волны вдоль и перпендикулярно оси скважины для разгруженного состояния и по величинам Aн и Aк, характеризующим отношение интегральной длины трещиноватости к величине интегрального раскрытия трещиноватости для соответствующего разгруженного или нагруженного состояния судят о зонах повышенной трещиноватости тела - сооружения в исследуемой скважине, кроме того, рассчитывают модуль упругости по величине равный статическому модулю упругости E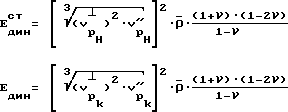
где  - среднее значение плотности по образцам,
- среднее значение плотности по образцам,
а модуль деформации находим с помощью выражения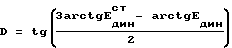
где D - модуль деформации, а Eдин - динамический модуль упругости для нагрузки испытываемой телом.
Техническая суть изобретения сводится к следующему.
Многие авторы основными факторами, определяющими различия между динамическим и статическим модулями упругости считают разный уровень действующих напряжений и существенно разную длительность силового воздействия.
В работе (Савич А.И., и Куюджич В.Д. Комплексные инженерногеофизические исследования при строительстве гидротехнических сооружений. - М.: Недра, 1990, с. 348-349) доказывается, что влияние длительности силового воздействия на различие между Eст и Eдин определяется термодинамическими особенностями процесса деформации и для горных пород не превышает 0,1%.
Величина силового воздействия не должна влиять на величины модулей упругости, так как модуль упругости характеризуется линейной частью диаграммы напряжение - деформация.
По мнению ряда авторов различие между статическим и динамическим модулями упругости определяется не столько термодинамикой процессов деформирования, сколько особенностями проявления упругого последействия. Указывается, что для получения сопоставимых значений модулей упругости, полученных разными способами Eст и Eдин необходимо отделить идеально-упругую деформацию εид от деформации упругого последействия εуп. Влияние упругого последействия менее всего сказывается на начальных и конечных частях диаграммы напряжение - деформация, поэтому для определения модуля упругости следует использовать начальную часть диаграммы напряжение - деформация.
Разница между искомыми величинами может заключаться в объеме исследуемого тела, подвергнувшегося силовому воздействию разного вида. При статических нагрузках образцы (часть массива) горных пород подвержены напряжениям в полном объеме своей массы, а при динамических нагрузках в результате возникновения волны воздействию подвергается только часть образца.
Вопросу о соотношении между статическим и динамическим модулями упругости посвящено много работ, но до настоящего времени нет общепринятых четко сформулированных положений, позволяющих находить сопоставимые значения указанных величин даже для скальных пород. Почти все авторы, производившие определения на образцах отмечают в общем малое различие модулей, не превышающее, как правило, нескольких десятков процентов. В тех же случаях, когда сопоставляются натурные определения, различия нередко достигают нескольких сот процентов.
В заявленном способе определения упомянутых выше параметров, во-первых, при оценке динамического модуля упругости не учитывается влияние напряженно-деформируемого состояния тела, сооружения, массива в точке исследования (изменение формы порового пространства в результате действия нагрузки), которое оказывает значительное влияние на величину скорости продольной волны, а величина скорости продольной волны, используемая в методике для расчета динамического модуля упругости взята в квадрате. Поэтому неправильность выбора значения скорости продольной волны для оценки динамического модуля упругости существенно искажает величину искомого параметра. Исследуемое тело - сооружение, массив находится под действием от точки к точке переменного по величине напряженного состояния, с соответствующей величиной деформации, которая может складываться как из упругой, так и остаточной составляющей. На поясняющем сущность изобретения чертеже приведена зависимость напряжение - деформация для исследуемого тела. По оси скважины это может быть точка A, B или C. В результате ультразвуковых исследований в рассматриваемой точке скважины (A, B, C) прикладывается дополнительная нагрузка Δσ, которой соответствует своя ΔεA, ΔεB или ΔεC величина деформации, а следовательно и разные по величине модули упругости. Оценка модуля упругости должна осуществляться относительно разгруженного состояния, как это осуществляется при оценке статического модуля упругости - по ветви разгрузки.
Следовательно, в формуле для расчета модуля упругости необходимо использовать величину скорости продольной волны, соответствующей разгруженному состоянию исследуемой точки тела.
Во-вторых, так как при статических исследованиях воздействию нагрузки подвергается вся масса исследуемого объема (для данной точки), а мы пытаемся оценить модуль упругости по величине равный статическому, целесообразно при расчете динамического модуля упругости использовать величину скорости продольной волны, соответствующую корреляционному (по трем направлениям 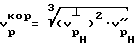 ) значению скорости для разгруженного состояния исследуемого объема.
) значению скорости для разгруженного состояния исследуемого объема.
Таким образом, задача сводится к нахождению корреляционного по трем направлениям значения скорости продольной волны, соответствующего разгруженному состоянию тела в рассматриваемой токе тела.
Теоретическое подтверждение возможности реализации заявленного способа заключается в следующем.
Так как мы хотим оценить модуль упругости, следует помнить, что при наличии упругих деформаций роста трещин при приложении нагрузки быть не должно, что описывается уравнением, определяющим неизменность площади поверхности интегральной трещиноватости при нагружении (решение о выдаче патента от 06 июля 1995 г. по заявке N 94022538/28 на изобретение "Способ определения деформационных характеристик материалов" тех же заявителей).
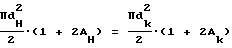
где
dн и dк - интегральная величина раскрытия трещиноватости для разгруженного и нагруженного состояний.
Aн и Aк - параметры формы порового пространства для разгруженного и нагруженного состояний.
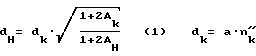
где
a - шаг применяемого ультразвукового зонда.
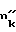 - пористость вдоль оси скважины для нагрузки испытываемой телом в момент проведения УЗК.
- пористость вдоль оси скважины для нагрузки испытываемой телом в момент проведения УЗК.
По уравнению "среднего времени"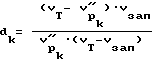
где
Vзап - скорость продольной волны в заполнителе.
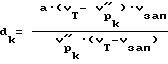
соответственно 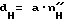
где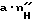 - интегральная величина раскрытия трещиноватости вдоль оси скважины на данном участке тела для разгруженного состояния.
- интегральная величина раскрытия трещиноватости вдоль оси скважины на данном участке тела для разгруженного состояния.
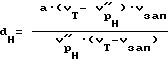
Запишем выражение (1) в виде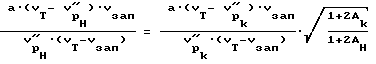
преобразуем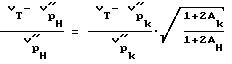
где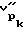 - скорость продольной волны вдоль оси скважины, полученная на исследуемой базе по материалам УЗК для нагрузки на момент исследования.
- скорость продольной волны вдоль оси скважины, полученная на исследуемой базе по материалам УЗК для нагрузки на момент исследования.
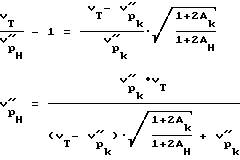
Параметр начальной формы порового пространства по прозвучиванию образцов описывается выражением (материалы заявки N 94022538/28)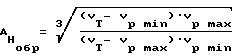
Коэффициент анизотропии определяется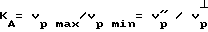
По материалам УЗК коэффициент анизотропия на момент проведения УЗК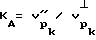
При УЗК параметр Aк является начальным для ультразвукового воздействия, поэтому Aк определяется выражением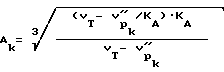
а коэффициент анизотропии равен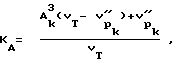
а скорость продольной волны перпендикулярно оси скважины для нагрузки испытываемой рассматриваемым участком тела в момент проведения УЗК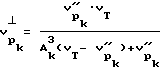
Интегральная длина трещиноватости на исследуемом участке для нагрузки в момент исследования - lк;
lk= b·n
где
b - зона ультразвукового воздействия,
n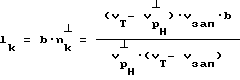
Интегральная длина трещиноватости на исследуемом участке для разгруженного состояния lн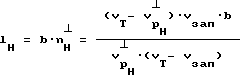
n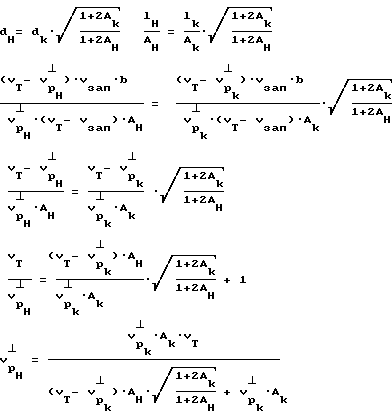
Значения скоростей продольной волны 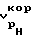 и
и 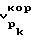 по выражениям
по выражениям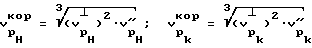
а динамический модуль упругости по величине равный статическому и динамический модуль упругости по выражениям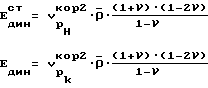
Тангенс угла наклона начального участка диаграммы tgα на чертеже отвечает статическому модулю упругости Eст. Проведем в некоторой точке C диаграммы касательную к кривой σ(ε). Тангенс угла наклона этой касательной с осью абсцисс tgβ определяет касательный модуль Ek= dσ/dε = tgβ.
Соединим точку C с началом системы координат 0, тангенс угла наклона этого отрезка будет соответствовать модулю деформации в рассматриваемой точке - tgγ.
Рассмотрим участок диаграммы σ(ε) - 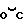 как дугу окружности и из точек касания 0 и C касательных, определяющих модули (упругости и касательный) восстановим перпендикуляры и продлим их до точки пересечения перпендикуляров S - центра окружности.
как дугу окружности и из точек касания 0 и C касательных, определяющих модули (упругости и касательный) восстановим перпендикуляры и продлим их до точки пересечения перпендикуляров S - центра окружности.
Углы, образованные полученными радиусами с вертикалью соответственно равны углам α и β, как углы, образованные взаимно перпендикулярными сторонами, а центральный угол, опирающийся на интересующую нас дугу 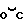 равен α - β.
равен α - β.
Угол, составленный касательной и хордой, измеряется половиной дуги, заключенной внутри него, следовательно угол AOC равен 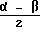 . Интересующий нас угол наклона отрезка OC с осью абсцисс равен разности углов α и
. Интересующий нас угол наклона отрезка OC с осью абсцисс равен разности углов α и 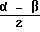 . Это угол
. Это угол 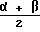 . Следовательно, модуль деформации равен тангенсу полусуммы углов α и
. Следовательно, модуль деформации равен тангенсу полусуммы углов α и 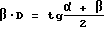 .
.
Тангенс угла наклона начального участка диаграммы отвечает статическому модулю упругости или, как отмечено выше, динамическому модулю упругости для разгруженного состояния tgα.
В точке C диаграммы форма порового пространства материала исследуемого тела изменена относительно разгруженного состояния приложенным напряжением σc. Следовательно, мы имеем другое состояние тела. Для оценки измененного состояния тела в точке C перенесем начало координат в рассматриваемую точку. Касательная, определяющая касательный модуль, должна в точке определять модуль упругости, поэтому развернем систему координат вокруг исследуемой точки C на угол α относительно касательной в точке C.
Произошел разворот осей координат на угол, равный - (α - β).
Ультразвуковая нагрузка в точке C мала относительно нагрузки, испытываемой телом (сооружением) и вызванная ей деформация мала, поэтому можно принять, что отношение приращений Δσ и Δε определяется касательным модулем. Таким образом, касательный модуль в рассматриваемой точке (в старой системе координат) есть динамический модуль упругости в новой системе координат.
Используя выражения для нахождения новых координат точки по ее старым координатам, динамический модуль упругости в точке можно найти с помощью выражения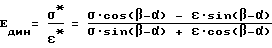
разделим числитель и знаменатель на ε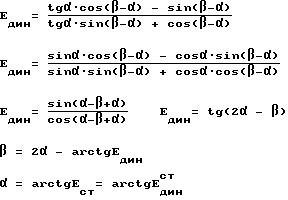
модуль деформации по выражению
Заявленное техническое решение является новым, так как характеризуется новой совокупностью существенных признаков, отсутствующей во всех аналогах.
Заявленные отличия при реализации сообщают объекту изобретения ряд полезных свойств, заключающихся в обеспечении возможности достаточно просто и достоверно оценивать по материалам ультразвукового каротажа упругие свойства тела и его состояние как по величине скоростей продольной волны в двух взаимноперпендикулярных направлениях, так и с помощью величин статических модулей упругости и модулей деформации, производить достоверную оценку трещиноватости тела, не искаженную и не маскирующуюся напряженным состоянием тела. Это свойство отсутствует у всех известных нам аналогов, является свойством заявленной совокупности признаков, что позволяет сделать вывод о соответствии заявленного решения критерию "изобретательский уровень".
Способ реализуется следующим образом:
1. Проводят ультразвуковой каротаж с получением встречных многоканальных осциллограмм.
2. Осуществляют обработку осциллограмм с составлением таблицы, в которую заносятся искомые величины 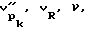 , Aк, Aн, а затем и
, Aк, Aн, а затем и 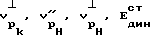 , Eдин, D.
, Eдин, D.
3. Находят отношение длины волны LR к периметру скважины 2πr0.
4. Используя дополненную номограмму Кнопова-Коптева по величине VR/VP с учетом αR/2πr0 находят величину коэффициента Пуассона ν.
5. Находят величину параметра формы порового пространства для нагруженного состояния по выражению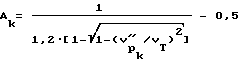
6. Находят величину параметра формы порового пространства для разгруженного состояния, решая уравнение A
p = 0,5+2Aк/y; q=Aк•(Aк+y)/y2
t=Aн/2y2•[1-(1+y)2•(1+2Aк)]
7. Зная величины Aк и Aн рассчитывают величины скоростей продольной волны для нагруженного и разгруженного состояний в двух взаимно перпендикулярных направлениях - параллельно и перпендикулярно оси скважины для каждого рассматриваемого участка скважины по выражениям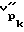 - известно по материалам УЗК;
- известно по материалам УЗК;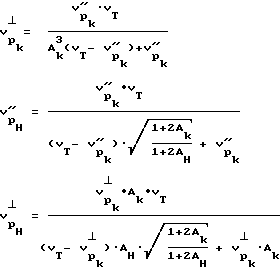
8. Сопоставляя изменения параметра формы порового пространства и скоростей продольной волны для разгруженного состояния с глубиной скважины производят оценку трещиноватости исследуемого тела по скважине.
9. Рассчитывают величины корреляционных значений скорости продольной волны для нагруженного и разгруженного состояния по выражениям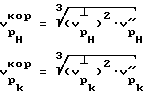
10. Рассчитывают модуль упругости по величине равный статическому модулю упругости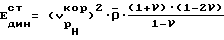
11. Рассчитывают динамический модуль упругости в рассматриваемой точке для нагрузки соответствующей моменту проведения УЗК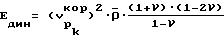
12. Находят модуль деформации в точке исследования для нагрузки испытываемой телом (сооружением) в момент проведения УЗК по выражениям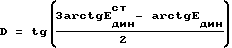
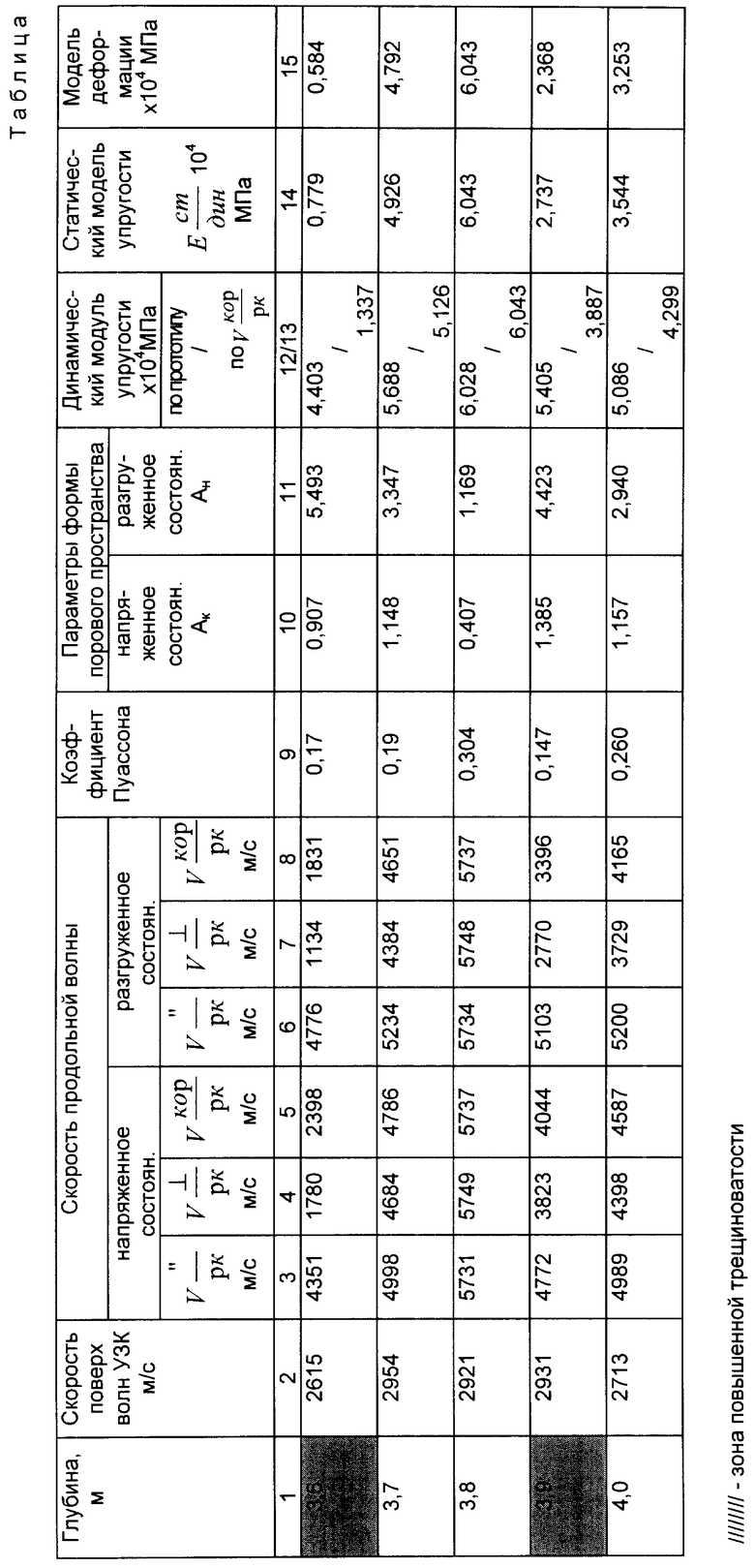
Пример применения предлагаемой методики представлен в таблице, в которую сведены результаты обработки встречных многоканальных осциллограмм для одной стоянки зонда, шаг зонда 0,1 м. Обработка многоканальных осциллограмм производилась по величине разности прихода волн в каждой соседней паре приемников. В таблицу сведены последовательно полученные по следующим выражениям параметры:
1. Столбец 2 и 3 - величины скоростей VR и 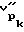 , полученные по осредненным временам прямой и встречной осциллограммы на базе равной шагу зонда.
, полученные по осредненным временам прямой и встречной осциллограммы на базе равной шагу зонда.
2. Столбец 9 - величина динамического коэффициента Пуассона ν, полученная по номограмме Кнопова-Коптева по величине отношения скоростей, с учетом влияния криволинейности границ вдоль которых распространяются упругие волны на характер волновой картины при УЗК скважин, для чего рассчитывают отношение длины регистрируемых волн LR к периметру скважины. Диаметр скважины 110 мм. Период волны TR = 32 мкс. Длина волны LR = VR•TR = 2606•32•10-6 ≈8,3 см
y = 0,19
3. Величина Aк (столбец 10)
4. Коэффициенты уравнения третьей степени вида A
p = 0,5 + 2Aк/y = 0,5 + 2•1,148/0,19 = 12,580
q = Aк•(Aк+y)/y2 = 1,148•(1,148+0,19)/0,192 = 42,549 Ан = 3,347
Ан = 3,347
5. Величины скоростей продольной волны вдоль оси скважины 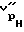 для разгруженного состояния (столбец 6)
для разгруженного состояния (столбец 6)
6. Скорость продольной волны перпендикулярно оси скважины для нагруженного состояния (столбец 4):
7. Величина скорости продольной волны перпендикулярно оси скважины для разгруженного состояния (столбец 7).
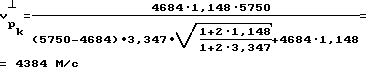
8. Корреляционные значения скорости продольной волны для разгруженного состояния - (столбец 8) и нагруженного - (столбец 5)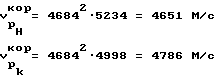
9. Величина модуля упругости равная соответствующей величине статического модуля упругости - (столбец 14)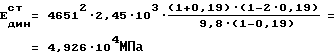
10. Величины динамического модуля упругости по корреляционному значению скорости и по величине скорости вдоль оси керна 0 (столбец 12, 13)
11. Модуль деформации - (столбец 15).

Использование заявляемого технического решения обеспечивает следующие технико-экономические преимущества:
1. Расширяет функциональные возможности ультразвуковых методов исследования.
2. Обеспечивает возможность масштабной, детальной оценки статического модуля упругости и модуля деформации по длине скважины.
3. Дает возможность оценки состояния тела, сооружения, массива - его трещиноватости на момент исследования по величинам скоростей в двух взаимно перпендикулярных направлениях для разгруженного состояния, оценки формы порового пространства и его изменение под действием нагрузки, испытываемой рассматриваемой точкой на момент исследования.
4. Данный вид исследования экономически выгоден относительно используемых геотехнических методов нахождения искомых деформационных параметров.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ НАХОЖДЕНИЯ ЛИНЕЙНЫХ ДЕФОРМАЦИОННЫХ ПАРАМЕТРОВ ИССЛЕДУЕМОГО ТЕЛА, СООРУЖЕНИЯ, МАССИВА | 1996 |
|
RU2115920C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ | 1993 |
|
RU2077714C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИОННЫХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 1994 |
|
RU2077811C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЛАВНЫХ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ В МАССИВЕ ГОРНЫХ ПОРОД | 1994 |
|
RU2064579C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ГЛАВНЫХ НОРМАЛЬНЫХ НАПРЯЖЕНИЙ В МАССИВЕ ГОРНЫХ ПОРОД И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1992 |
|
RU2029084C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МОДУЛЯ ДЕФОРМАЦИИ МАТЕРИАЛЬНОЙ СРЕДЫ | 2014 |
|
RU2566400C1 |
| СПОСОБ И УСТРОЙСТВО ДЛЯ ИСПЫТАНИЯ ГРУНТОВ СТАТИЧЕСКОЙ И ДИНАМИЧЕСКОЙ НАГРУЗКОЙ | 2010 |
|
RU2446251C1 |
| Способ определения удароопасности участков массива горных пород | 1989 |
|
SU1694893A1 |
| Способ определения механических свойств горного массива | 1984 |
|
SU1183676A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ МАТЕРИАЛА С ХРУПКИМ СКЕЛЕТОМ | 2013 |
|
RU2543709C2 |
Способ предназначен для использования в области инженерной геологии и геофизики. Способ оценки состояния тела - его трещиноватости, статического модуля упругости и модуля деформации основан на возможности учета влияния дефектов на исследуемые параметры по двум взаимноперпендикулярным направлениям и их изменений в результате приложения нагрузки. Способ дает возможность определения состояния тела - сооружения, массива - его трещиноватости на момент исследования по величине скоростей в двух взаимно перпендикулярных направлениях для разгруженного и нагруженного состояний. Позволяет оценить форму порового пространства и его изменение под действием нагрузки, испытываемой рассматриваемой точкой тела на момент исследования. 1 ил., 1 табл.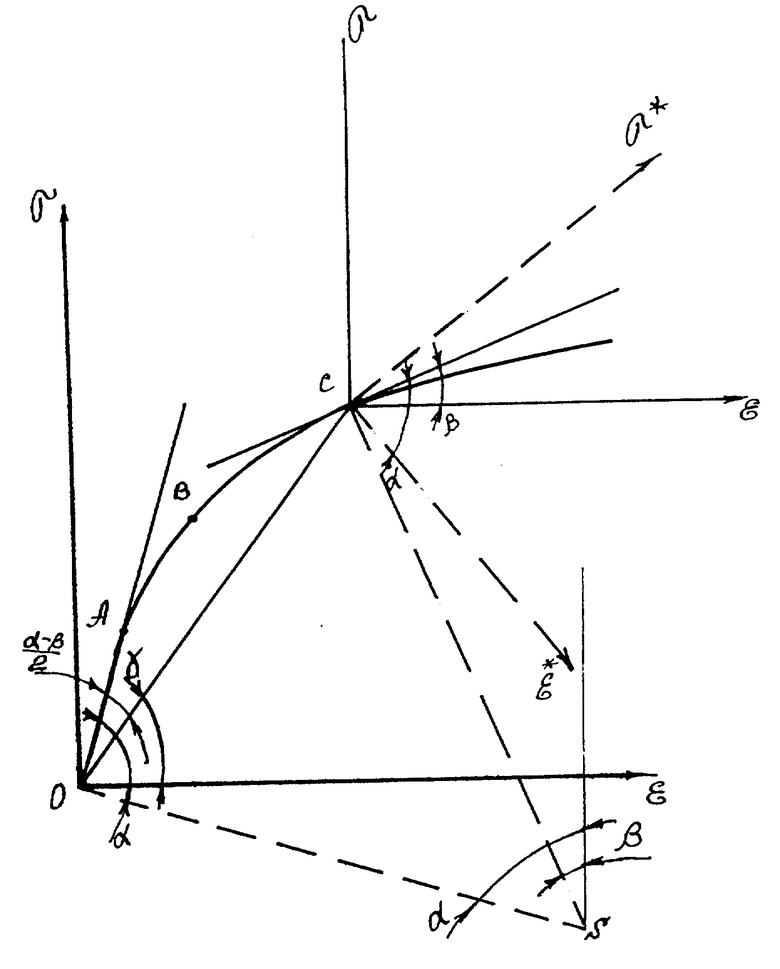
Способ определения состояния и деформационных параметров тела, сооружения, массива, включающий проведение наблюдений с помощью ультразвукового каротажа (УЗК) скважины и выделение по многоканальным встречным осциллограммам упругих волн двух типов P и R, расчет скоростей этих волн VP и VR и их отношения VR/VP, оценку отношения длины волны LVR к периметру скважины 2πro и по величине отношения скоростей с учетом величины LR/2πro по дополненной номограмме Кнопова-Коптева нахождение коэффициента Пуассона ν и динамического модуля упругости, отличающийся тем, что рассчитывают величину конечного параметра формы порового пространства Ак для нагрузки, испытываемой телом в данной точке в момент проведения УЗК, по выражению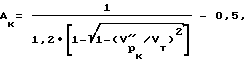
где 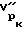 - скорость продольной волны вдоль оси скважины для нагрузки, испытываемой телом в данной точке;
- скорость продольной волны вдоль оси скважины для нагрузки, испытываемой телом в данной точке;
Vт - скорость продольной волны в скелете материала,
затем решают уравнение третьей степени вида
Ан 3 + рАн 2 + gАн + t = 0 относительно Ан,
где Ан - начальный параметр формы порового пространства для разгруженного состояния, коэффициенты которого рассчитывают по выражениям
p = 0,5+2Aк/ν,
g = Aк•(Aк+ν)/ν2,
t = A
после чего рассчитывают величины скоростей продольной волны для напряженного состояния в рассматриваемой точке тела перпендикулярно к оси скважины 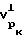 по выражению
по выражению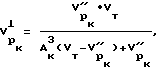
для разгруженного состояния вдоль оси скважины 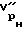 и перпендикулярно оси скважины
и перпендикулярно оси скважины 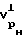 по выражениям
по выражениям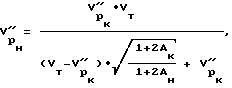
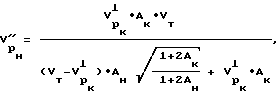
затем по величинам скоростей продольных волн вдоль и перпендикулярно к оси скважины для нагруженного и разгруженного состояний и по величинам Ан и Ак судят о зонах повышенной трещиноватости тела, сооружения, массива в исследуемой скважине, кроме того, рассчитывают модуль упругости, по величине равный статическому модулю упругости E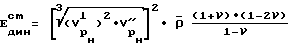
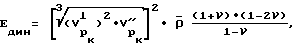
где  среднее значение плотности по образцам,
среднее значение плотности по образцам,
а модуль деформации D определяют по выражению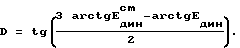 е
е
| Савич А.И | |||
| и др | |||
| Сейсмоакустические методы изучения массивов скальных пород | |||
| - М.: Недра, 1969, с.155 - 166. |
Авторы
Даты
1998-07-20—Публикация
1996-10-01—Подача