Изобретение относится к инженерной геологии и геофизике. Данная техническая задача имеет важное значение при решении большого числа инженерных задач, связанных с вопросами строительства, оценки состояния, эксплуатации и проектирования сооружений и механизмов, технологической обработки материалов и других вопросов.
Для оценки напряженного состояния необходимо знать компоненты деформации в исследуемой точке сооружения или массива.
Деформации или относительные удлинения на поверхности обычно измеряют с помощью электрических тензодатчиков [1].
Тензодатчик - это короткий кусок проволоки, изолированный от поверхности исследуемого объекта и приклеенный к нему. Когда возникает удлинение, электрическое сопротивление проволоки увеличивается и в силу этого можно измерять деформацию электрическим способом. Этот эффект усиливается укладыванием проволоки в петли. Проволока вклеивается между кусочками бумаги и вся система наклеивается на поверхность исследуемого объекта.
Основными недостатками аналога являются:
1. Возможность измерения деформации в одной точке - поверхности, на которую наклеен датчик.
2. Сложность и большая стоимость исследований.
3. Частый выход из строя тензодатчиков в течение эксплуатации.
4. Изменение параметров тензодатчиков во времени. Необходимость периодических тарировок тензодатчиков.
Известен способ определения коэффициента Пуассона по данным ультразвукового каротажа (УЗК) [2].
В данном методе проводится ультразвуковой каротаж с получением многоканальных встречных осциллограмм. Обработка осциллограмм осуществляется в следующем порядке:
а) производится выделение и корреляция выбранных фаз основных волн на осциллограммах УЗК;
б) снимаются времена прихода выделенных фаз колебаний;
в) вычисляются средние приращения времен прихода волн из двух встречных наблюдений на исследуемой базе (шаг зонда);
г) вычисляются скорости волн P и R по полученным значениям времени ΔtP и ΔtR ;
д) составляются таблицы значений ΔtP и ΔtR для волн P и R на исследуемой базе по всей глубине скважины;
е) рассчитывается отношение скоростей выделенных волн VR/VP.
По данным УЗК, кроме скорости продольных волн VP, уверенно определяется лишь скорость поверхностных волн на цилиндрической поверхности VR, которая зависит от отношения длины волны LR к периметру скважины 2πr0 , поэтому коэффициент Пуассона находится по номограмме Кнопова-Коптева по величине отношения VR/VP с учетом отношения LR/2πr0.
Данное техническое решение выбрано в качестве прототипа, так как в нем также, как и в предлагаемом методе, осуществляют ультразвуковой каротаж исследуемой скважины, нахождение и расчет скоростей двух типов волн, анализ типов волн и нахождение величин коэффициента Пуассона.
Основным недостатком прототипа является невозможность нахождения величин абсолютных линейных деформаций для рассматриваемой нагрузки сооружения (массива) относительно разгруженного состояния.
Целью изобретения является масштабная оценка величин абсолютных линейных деформаций, вызванных силовыми воздействиями на сооружение относительно разгруженного состояния в пределах исследуемой скважины по материалам ультразвукового каротажа. Согласно изобретению способ определения деформационных параметров тела, сооружения, массива, включающий проведение наблюдений с помощью ультразвукового каротажа скважины и выделение по многоканальным встречным осциллограммам упругих волн двух типов P и R с расчетом скоростей этих волн и их отношения VR/VP, оценку отношения длины волны LR к периметру скважины 2πr0 , и по величине отношения скоростей с учетом величины LR/2πr0 по дополненной номограмме Кнопова-Коптева нахождение коэффициента Пуассона ν , отличается тем, что для оценки распределения величин абсолютных деформаций по скважине рассчитывают величину конечного параметра формы порового пространства Aк для нагрузки, испытываемой сооружением в данной точке в момент исследования, по выражению: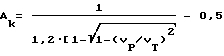 ,
,
где
VT - скорость продольной волны в скелете материала,
VP - скорость продольной волны в рассматриваемой точке, затем, решая уравнение третьей степени вида:
A
где Aн - начальный параметр формы порового пространства для разгруженного состояния, коэффициенты уравнения рассчитываются следующим образом: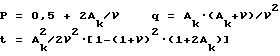
и по величинам Aк и Aн находим величины абсолютных линейных деформаций в каждой рассматриваемой точке скважины - εk (деформации параллельно оси скважины) и εx (деформации перпендикулярно оси скважины) по выражениям: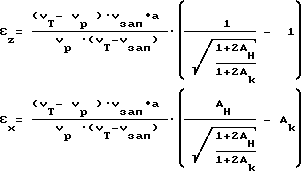
где
Vзап - скорость продольной волны в заполнителе,
а - шаг применяемого ультразвукового зонда.
Сущность изобретения понятна из вывода предлагаемых выражений. Предлагаемый способ оценки абсолютных линейных деформаций основан на определении понятия коэффициента Пуассона как отношения относительных поперечных деформаций к относительным продольным деформациям, рассматриваются деформации при приложении нагрузки относительно ненагруженного состояния.
В предлагаемом способе проводятся исследования в скважине нагруженной конструкции, в которой по общепринятой методике определяется величина динамического коэффициента Пуассона.
В настоящее время известен способ определения коэффициента Пуассона при помощи выражения: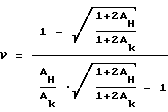
(Решение о выдаче патента от 06 июля 1995 г по заявке N 94022538/28 "Способ определения деформационных характеристик материалов"). Данное выражение показывает зависимость коэффициента Пуассона от изменения формы порового пространства.
Таким образом, зная величину коэффициента Пуассона и зная величину коэффициента формы порового пространства Aк для нагруженного состояния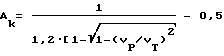 ,
,
можно найти величину коэффициента формы порового пространства для разгруженного состояния Aн. Мы как бы моделируем состояние разгрузки по величине коэффициента Пуассона.
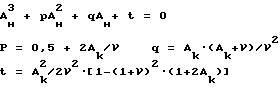
Зная величины начальной и конечной формы порового пространства в каждой точке, находим отношение интегральных величин раскрытия трещиноватости после приложения нагрузки dк к интегральной величине раскрытия трещиноватости до приложения нагрузки dн: 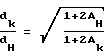
Для расчета интегральной величины раскрытия трещиноватости после приложения нагрузки может быть использовано так называемое "уравнение среднего времени", из которого в долях единицы находится величина трещинной пустотности на исследуемой базе. Исследуемая база а - это шаг применяемого ультразвукового зонда. Уравнение среднего времени может быть использовано для определения трещинной пустотности, так как обычно используются упругие колебания, длина волн которых значительно больше размеров структурных элементов трещиноватой среды.
Величина трещинной пустотности в направлении, параллельном оси скважины, n'' для данной нагрузки из уравнения среднего времени: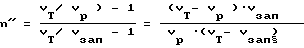
Известна база прозвучивания. Известна величина пористости на этой базе, следовательно, может быть определена интегральная величина раскрытия трещиноватости в ненагруженном состоянии - dн, так как 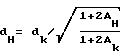
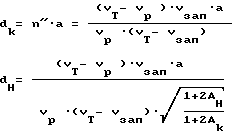
Величина абсолютной линейной деформации для данной нагрузки в каждой конкретной точке исследуемой скважины относительно ненагруженного состояния по оси скважины εz определяется выражением: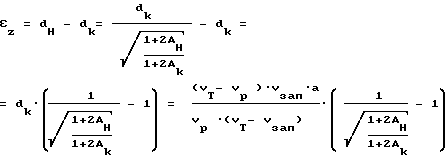
Искомые величины измеряются в мм, так как величина а - шаг применяемого зонда измеряется в мм.
Величина искомой деформации для данной нагрузки в каждой конкретной точке относительно ненагруженного состояния перпендикулярна оси скважины εx определяется выражением: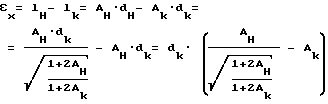
где
lн и lк - интегральная длина трещиноватости соответственно до и после нагрузки.
Aн = lн/dн; Aк = lк/dк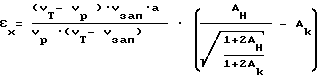
Заявленное техническое решение является новым, так как характеризуется новой совокупностью существенных признаков, отсутствующей во всех аналогах.
Заявленные отличия при реализации сообщают объекту изобретения ряд новых полезных свойств, заключающихся в обеспечении возможности достаточно просто и достоверно находить величины абсолютных линейных деформаций по скважине, что может послужить базой для оценки напряженного состояния исследуемого тела.
Это свойство отсутствует у всех известных нам аналогов, является свойством заявленной совокупности признаков, что позволяет сделать вывод о соответствии заявленного решения критерию "изобретательский уровень".
Способ реализуется следующим образом:
1. Проводится ультразвуковой каротаж с получением встречных многоканальных осциллограмм.
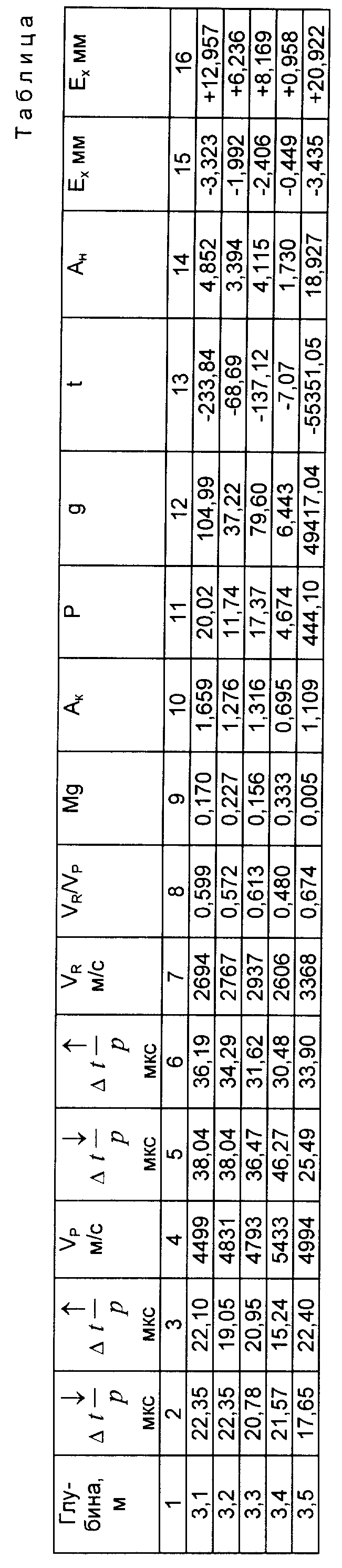
2. Осуществляется обработка осциллограмм с составлением таблиц, в которые заносятся искомые и расчетные значения 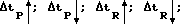 VP; VR; VR/VP; ν Aк; p; q; t; Aн εz и εx
VP; VR; VR/VP; ν Aк; p; q; t; Aн εz и εx
3. Находят отношение длины волны LR к периметру скважины 2πr0 .
4. Используя номограмму Кнопова-Коптева по величине VR/VP с учетом LR/2πr0 , находим величину коэффициента Пуассона ν .
5. Находим величину параметра формы порового пространства нагруженного состояния по выражению: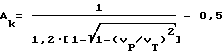
6. Находим величину параметра формы порового пространства для разгруженного состояния, решая уравнение: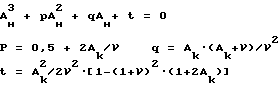
7. Зная величины Aк и Aн, рассчитываем величины абсолютных линейных деформаций вдоль оси скважины εz и перпендикулярно оси скважины εx/ по выражениям: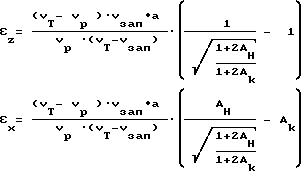
где
Vзап - скорость продольной волны в заполнителе,
а - шаг применяемого зонда.
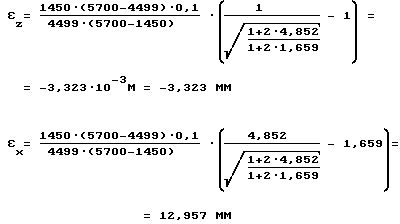
Пример применения предлагаемой методики представлен таблицей, в которую сведены результаты обработки встречных многоканальных осциллограмм для одной стоянки зонда. Шаг применяемого зонда а = 0,1 м. Обработка многоканальных осциллограмм производилась по величине разности прихода волн в каждой соседней паре приемников. В таблицу сведены все расчетные последовательно полученные по следующим выражениям параметры:
1. Столбцы 2, 3, 5, 6 - разности прихода волн ΔtP и ΔtR в каждой паре соседних приемников (прямые и встречные осциллограммы).
2. Столбцы 4 и 7 - величины скоростей волн VP и VR, рассчитанные по осредненным временам прямой и встречной осциллограммы на базе, равной шагу зонда.
3. Столбец 8 - рассчитывается величина отношения скоростей волн VR/VP.
4. Учитываем влияние криволинейности границ, вдоль которых распространяются упругие волны, на характер волновой картины при ультразвуковом каротаже скважин, для этого рассчитываем отношение длины регистрируемых волн к периметру скважины. Диаметр скважины 110 мм. Период волны T = 32 мкс; VR = 2606 м/с. Длина волны LR = VR•T = 2606 • 32 • 10-6 ≈ 8,3 см
LR/2πr0 = 8,3/3,14•11 ≈ 0,24 (округляем до 0,2)
Зная величину VR/VP и величину LR/2πr0 , по номограмме Кнопова-Коптева находим величину коэффициента Пуассона ν (столбец 9).
5. Рассчитываем величины Aк (столбец 10) по выражению: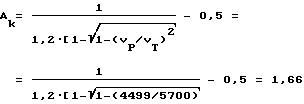
6. Рассчитываем величины Aн и коэффициенты уравнения:
A
Коэффициенты уравнения: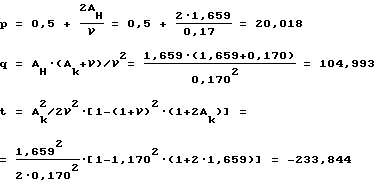
Корни уравнения третьей степени следующие:
Aн1 = 1,663 Aн2 = -10,841 Aн3 = 4,852
Искомое значение корня уравнения Aн = 4,852
Рассчитываем величины абсолютных деформаций вдоль и перпендикулярно оси скважины (столбцы 15 и 16).
Использование заявляемого технического решения обеспечивает следующие технико-экономические преимущества:
1. Расширение функциональных возможностей ультразвуковых методов исследования.
2. Обеспечивает возможность масштабной детальной оценки абсолютных деформаций в двух взаимно перпендикулярных направлениях по оси скважины.
3. Обеспечивает базу для детальной оценки напряженного состояния - оценки полного тензора напряжений в теле, сооружении, массиве с помощью одной скважины (продольного профилирования).
4. Данный вид исследования очень дешев относительно известных методов нахождения искомых параметров.
5. Возможность оценки предлагаемых параметров по уже имеющимся материалам исследования, используемых для оценки упругих параметров при определении упругих свойств материалов.
6. Вероятная возможность промышленного применения заявленного технического решения не вызывает сомнений, т.к. оно может быть реализовано с использованием серийно выпускаемой аппаратуры.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ СОСТОЯНИЯ И ДЕФОРМАЦИОННЫХ ПАРАМЕТРОВ ТЕЛ, СООРУЖЕНИЙ, МАССИВОВ | 1996 |
|
RU2115919C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ФИЗИКО-МЕХАНИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ | 1993 |
|
RU2077714C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДЕФОРМАЦИОННЫХ ХАРАКТЕРИСТИК МАТЕРИАЛОВ | 1994 |
|
RU2077811C1 |
| Способ определения трещинной пористости горных пород | 2015 |
|
RU2615051C1 |
| СПОСОБ И СИСТЕМА КОМБИНИРОВАННОГО СОПРОВОЖДЕНИЯ ПРОЦЕССА БУРЕНИЯ СКВАЖИНЫ | 2018 |
|
RU2687668C1 |
| Способ определения геологических свойств терригенной породы в около скважинном пространстве по данным геофизических исследований разрезов скважин | 2003 |
|
RU2219337C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МЕХАНИЧЕСКИХ СВОЙСТВ ПОРОДЫ ПЛАСТА-КОЛЛЕКТОРА | 2016 |
|
RU2636821C1 |
| Способ с.м.вдовина акустического каротажа | 1978 |
|
SU744411A1 |
| Акустический способ определения упругих констант токопроводящих твёрдых тел | 2017 |
|
RU2660770C1 |
| СПОСОБ ВЫБОРА БУРОВОГО РАСТВОРА ДЛЯ СТРОИТЕЛЬСТВА НАКЛОННЫХ И ГОРИЗОНТАЛЬНЫХ СКВАЖИН, ПРОБУРЕННЫХ В НЕУСТОЙЧИВЫХ ГЛИНИСТЫХ ОТЛОЖЕНИЯХ | 2016 |
|
RU2620822C1 |
Изобретение предназначено для использования в инженерной геологии и геофизике при решении задач, связанных с проектированием, строительством, а также оценкой состояния безопасности сооружений и механизмов, технологической обработки материалов и др. Способ основан на определении понятия коэффициента Пуассона как отношения относительных поперечных деформаций к относительным продольным деформациям. Деформации рассматриваются при приложении нагрузки относительно ненагруженного состояния. Способ расширяет функциональные возможности ультразвуковых методов исследования. Обеспечивает возможность масштабной детальной оценки абсолютных деформаций в двух взаимно перпендикулярных направлениях по оси скважины и полного тензора напряжений тела, сооружения, массива с помощью одной скважины. 1 табл,
Способ нахождения линейных деформационных параметров тела, сооружений, массива, включающий проведение наблюдений с помощью ультразвукового каротажа скважины и выделение по многоканальным встречным осциллограммам упругих волн двух типов Р и R с расчетом скоростей этих волн и их отношения, оценку отношения длины волны к периметру скважины и по величине отношения скоростей с учетом величины LR/2πro по дополненной номограмме Кнопова нахождение коэффициента Пуассона ν, отличающийся тем, что для оценки распределения величин абсолютных деформаций по скважине рассчитывают величину конечного параметра порового пространства Ак для нагрузки, испытываемой телом, сооружением, в данной точке в момент исследования, по выражению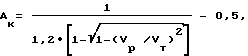
где Vт - скорость продольной волны в скелете материала;
Vр - скорость продольной волны в рассматриваемой точке,
затем решают уравнение третьей степени вида
A
где Ан - начальный параметр формы порового пространства для разгруженного состояния, а коэффициенты уравнения рассчитываются по выражениям
p = 0,5+2Aк/ν;
t = A
g = Aк•(Aк+ν)/ν2
и по величинам Ак и Ан находят величины абсолютных линейных деформаций в каждой рассматриваемой точке скважины параллельно оси скважины и перпендикулярно оси скважины по выражениям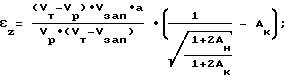
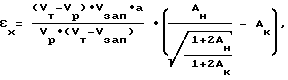
где Vзап - скорость продольной волны в заполнителе;
а - шаг применяемого ультразвукового зонда;
εz - деформации параллельно оси скважины;
εx - деформации перпендикулярно оси скважины.
| M.Hetenyi (ed) Handbook of Experimental stress Analysis, гл.5, 9, New York, 1950, ОСТ 34-72-647-83, ОСТ 34-72-652-83 | |||
| Савич А.И | |||
| и др | |||
| Сейсмоакустические методы изучения массивов скальных пород | |||
| - М.: Недра, 1969, с.155 - 167. |
Авторы
Даты
1998-07-20—Публикация
1996-06-06—Подача