Изобретение относится к строительству и предназначено для возведения сфероидальных куполов и конструкций. Известны многогранные конструкции, приближающиеся по форме к сфере и эллипсоиду /патенты США 4679361, 1987, 4825602, 1989/, состоящие из пятиугольных и шестиугольных панелей.
Недостатком данного технического решения является небольшая прочность конструкций в вершинах многогранников, образованных примыканием 4 граней. В этих вершинах велика вероятность расхождения швов купола. Широко известна и используется наиболее прочная сборка куполов, когда каждый вертикальный шов перекрывается гранью следующего верхнего пояса, например, додекаэдр и усеченный икосаэдр, имеющие трехгранные вершины.
Пятиугольные грани, расположенные в следующем от экваториального ряду, не являются симметричными фигурами, что усложняет сборку купола. Из статьи в "Scientific American", 1989, можно сделать вывод, что купол рассчитывался последовательно по кольцам из многоугольника, точки касания граней к воображаемому эллипсоиду, длины сторон и внутренние углы граней выбирались случайно. Такой метод расчета отрицательно влияет на прочность и надежность конструкции в целом.
Целью изобретения является упрощение сборки конструкции, повышение надежности и прочности купола.
Сущность изобретения заключается в том, что многогранная сфероидальная конструкция содержит 50 симметричных граней 5 типов /фиг. 1, 2, 13/. Верхним и нижним основаниями конструкции служат правильные шестиугольные грани 5 /фиг. 12/.
Конструкция состоит из пяти поясов:
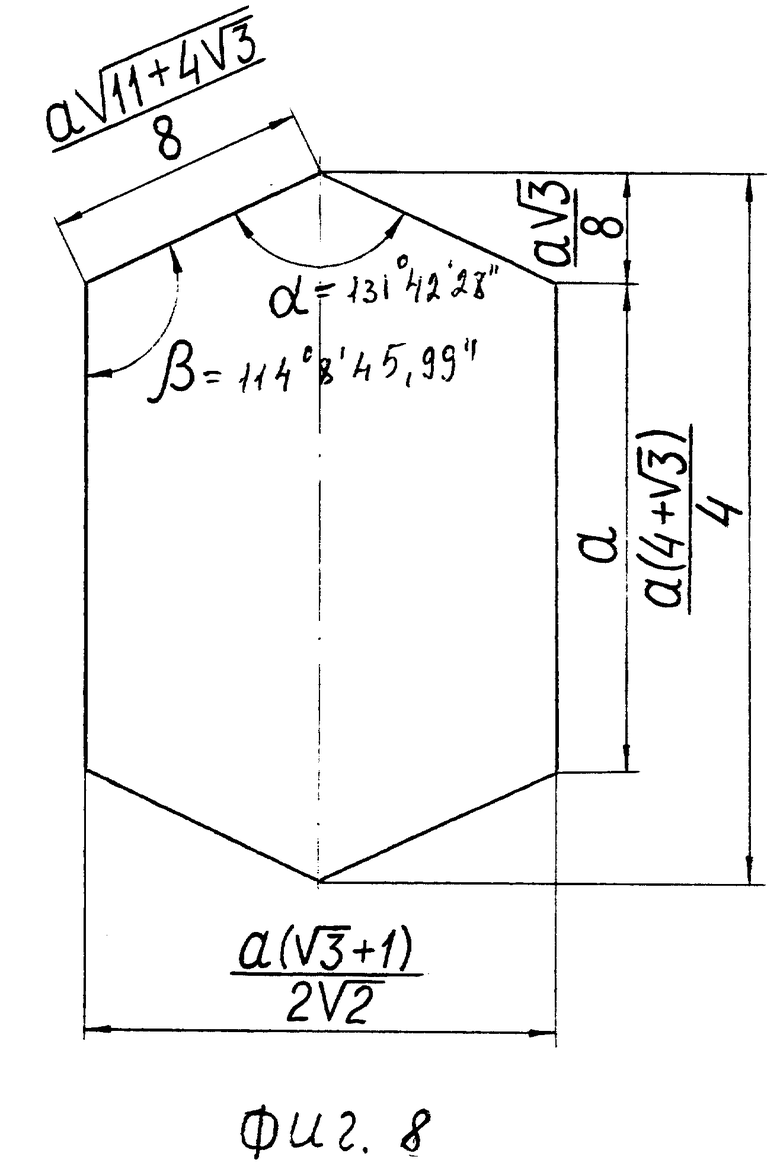
- экваториального пояса, содержащего двенадцать шестиугольных граней 1 /фиг. 8/,
- двух одинаковых поясов, симметрично расположенных относительно экватора, каждый пояс содержит шесть шестиугольных граней 4 /фиг. 11/ и примыкает к основанию,
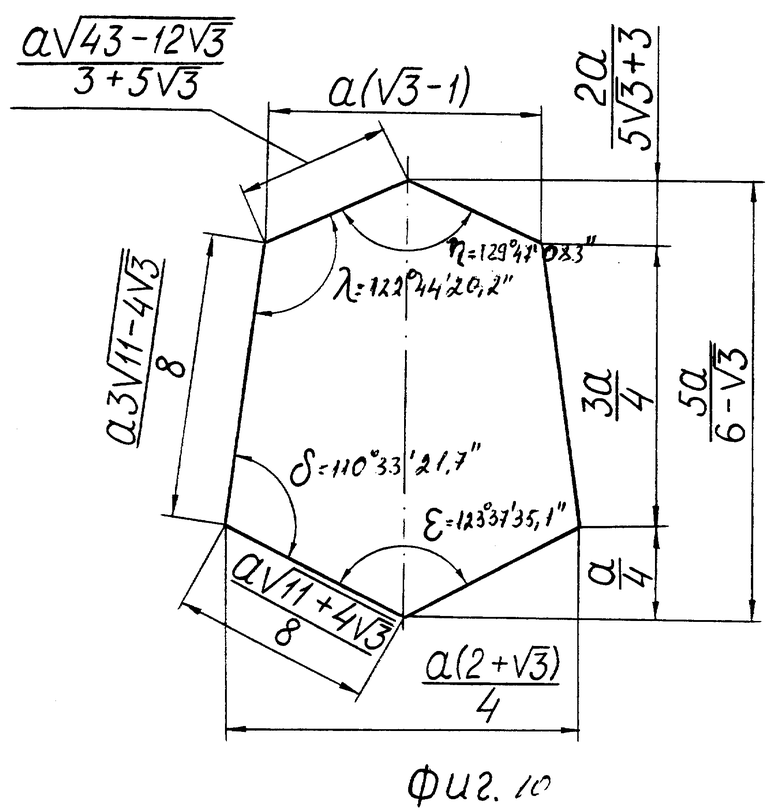
- двух одинаковых поясов, симметрично расположенных относительно экватора, каждый пояс содержит чередующиеся шесть пятиугольных 2 /фиг. 9/ и шесть шестиугольных 3 /фиг. 10/ граней и примыкает к экваториальному поясу.
Многогранник имеет 96 трехгранных вершин.
При мысленном рассечении многогранника 4 плоскостями симметрии 3 плоскостями, проходящими через середины сторон правильных шестиугольных оснований, и 1 плоскостью, проходящей через экватор, в сечениях получаются правильные двенадцатиугольники /фиг. 3-7/. Такой конфигурацией конструкции обеспечивается прочность, общая устойчивость формы и пространственная жесткость. Плоскости симметрии, проходящие через середины сторон правильных шестиугольных оснований, дают в сечениях 3 равных двенадцатиугольника /фиг. 6, сечение Б-Б/. Полагая, что стороны этого двенадцатиугольника равны "a", вычислены элементы пятиугольных и шестиугольных граней многогранника. Для расчета элементов многогранника с любой степенью точности они представлены в виде иррациональных выражений. Как образец, можно привести такое же представление элементов выпуклых правильных /тело Платона/ и полуправильных /тело Архимеда/ многогранников через длину стороны правильной многоугольной грани.
В конструкции вписывается сфера диаметром 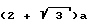 и эллипсоид /овалоид/ вращения, близкий к сфере /сфероид/, точки касания поверхности эллипсоида с гранями конструкции находятся на осях симметрии и совпадают, грани 1 и 5 находятся рядом, грани 2, 3, 4 с центрами тяжести граней /фиг. 16 - 18, 20, 21, 22 - 26/. Шестиугольная грань 3 больше пятиугольной грани 2 на величину равнобедренного треугольника с основанием, равным
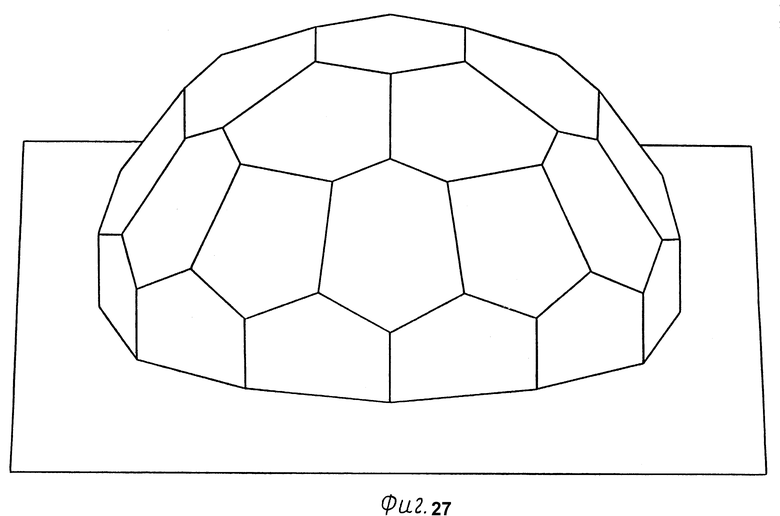
и эллипсоид /овалоид/ вращения, близкий к сфере /сфероид/, точки касания поверхности эллипсоида с гранями конструкции находятся на осях симметрии и совпадают, грани 1 и 5 находятся рядом, грани 2, 3, 4 с центрами тяжести граней /фиг. 16 - 18, 20, 21, 22 - 26/. Шестиугольная грань 3 больше пятиугольной грани 2 на величину равнобедренного треугольника с основанием, равным 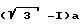 фиг. 9, 10/. На основе половины конструкции можно получить два типа куполов /фиг. 27, 28/, в основании каждого из которых лежит правильный двенадцатиугольник /фиг. 5, 6, сечения А-А, Б-Б/. Наилучший вариант купола /фиг. 27/, при котором пятиугольники в основании составляют с фундаментом прямой угол, благодаря чему обеспечивается сооружение купола.
фиг. 9, 10/. На основе половины конструкции можно получить два типа куполов /фиг. 27, 28/, в основании каждого из которых лежит правильный двенадцатиугольник /фиг. 5, 6, сечения А-А, Б-Б/. Наилучший вариант купола /фиг. 27/, при котором пятиугольники в основании составляют с фундаментом прямой угол, благодаря чему обеспечивается сооружение купола.
Площадь поверхности конструкции:
Объем конструкции: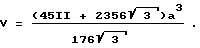
Осуществимо изменение высоты и объема конструкции, этого можно добиться, уменьшая или увеличивая длину грани 1 /фиг. 29/.
Возможность осуществления изобретения подтверждается интересом домостроительных компаний к аналогичному изобретению и открытием консультативной фирмы по его продаже в США.
Перечень чертежей.
Фиг. 1 - вид спереди /главный вид/ многогранной сфероидальной конструкции с нанесением номеров граней. Изображение по методу прямоугольного проецирования.
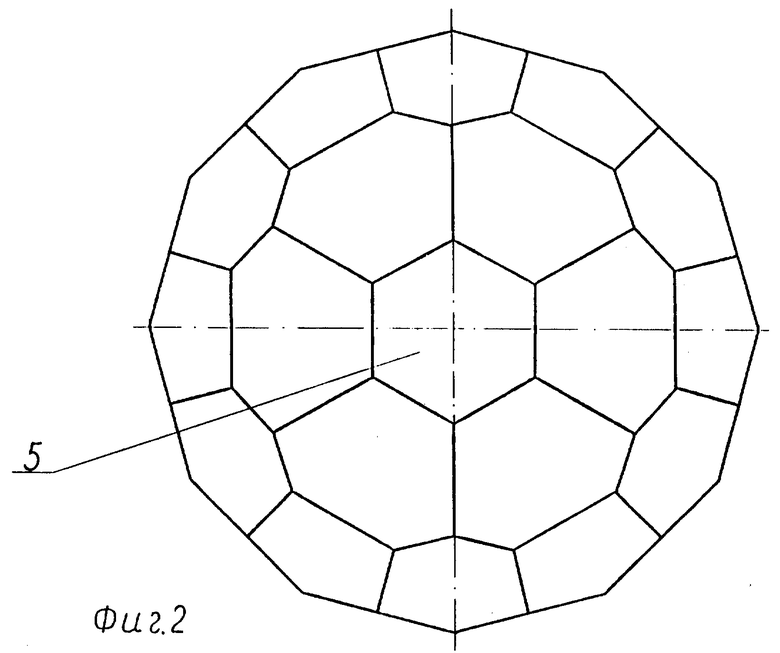
Фиг. 2 - вид сверху на фиг. 1 с нанесением номеров грани.
Фиг. 3 - сечение конструкции /изображения, получающиеся при мысленном рассечении конструкции плоскостями симметрии/, вид спереди.
Фиг. 4 - вид сверху на фиг. 3.
Фиг. 5 - сечение А-А, проходящее через экватор на фиг. 3 /правильный двенадцатиугольник/.
Фиг. 6 - сечение Б-Б, проходящее через середины сторон правильных шестиугольных оснований, на фиг. 4/ правильный двенадцатиугольник/.
Фиг. 7 - сечение В-В, проходящее через вершины правильных шестиугольных оснований на фиг. 4 - правильный двенадцатиугольник/.
Фиг. 8 - шестиугольная грань 1.
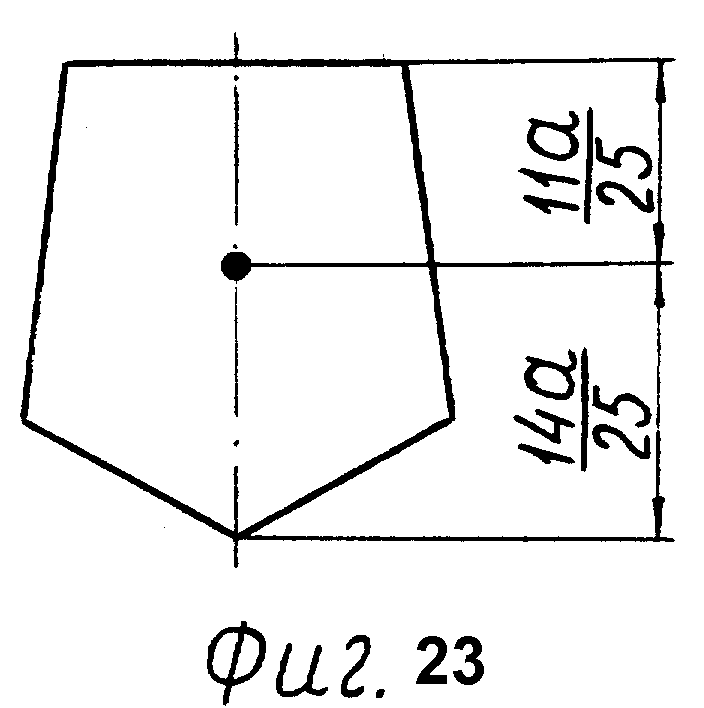
Фиг. 9 - шестиугольная грань 2.
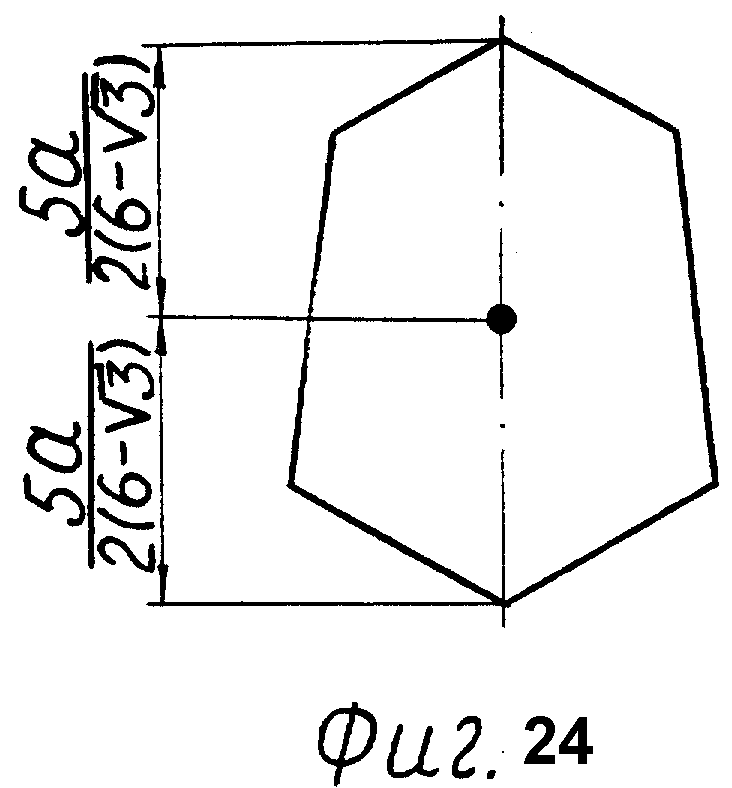
Фиг. 10 - шестиугольная грань 3.
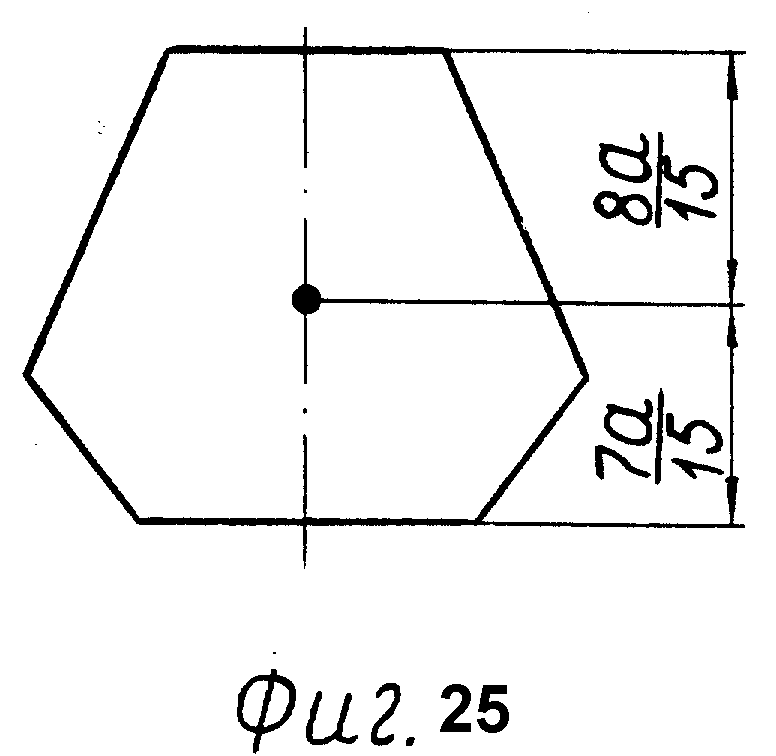
Фиг. 11 - шестиугольная грань 4.
Фиг. 12 - шестиугольная грань 5.
Фиг. 13 - изображение конструкции в диметрии.
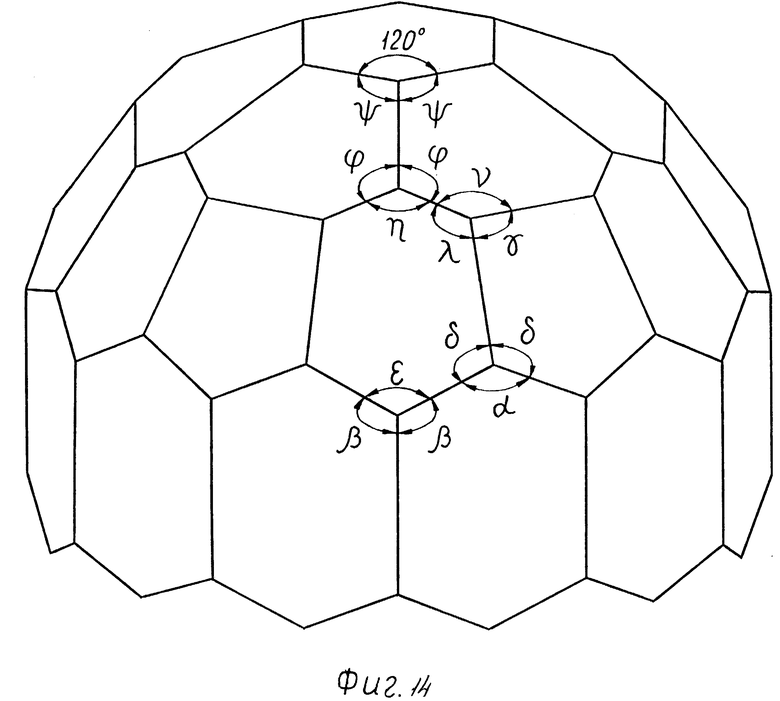
Фиг. 14 - двугранные углы конструкции.
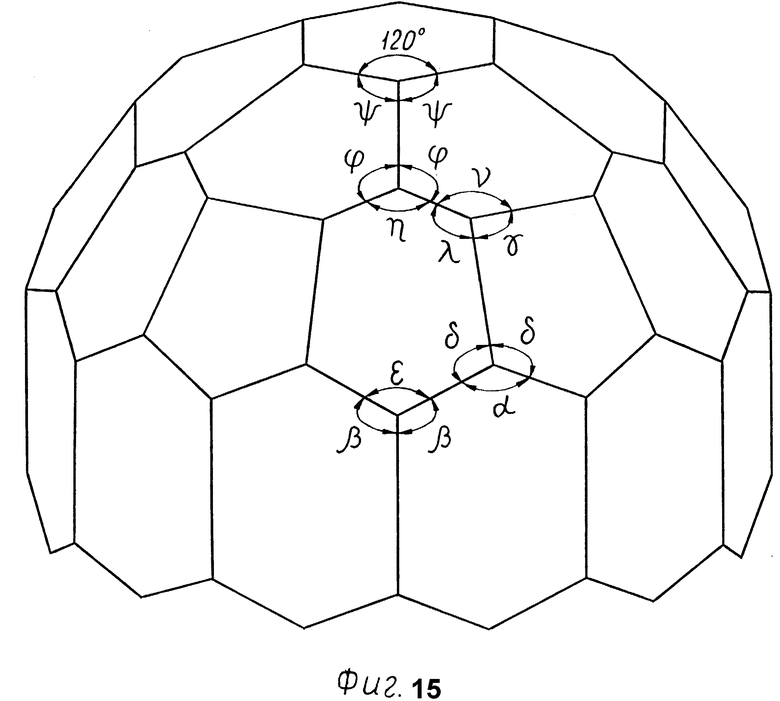
Фиг. 15 - суммы плоских углов, сходящихся в вершинах.
Фиг. 16 - эллипсоид, вписываемый в конструкцию. Вид спереди.
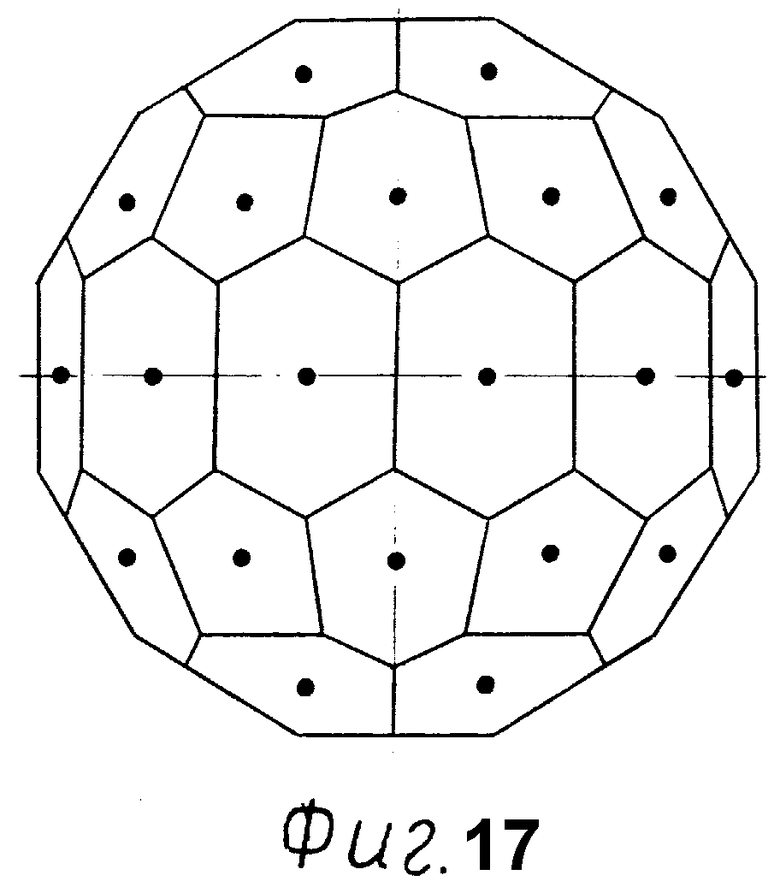
Фиг. 17 - точки касания эллипсоида с гранями. Вид спереди.
Фиг. 18 - эллипсоид, вписываемый в конструкцию. Вид сверху.
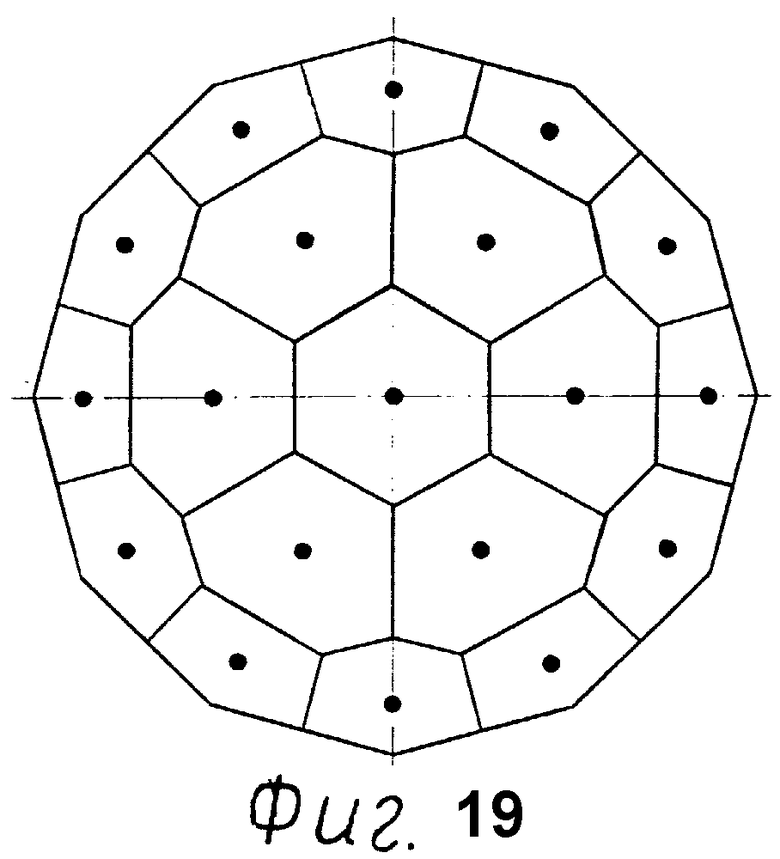
Фиг. 19 - точки касания эллипсоида с гранями. Вид сверху.
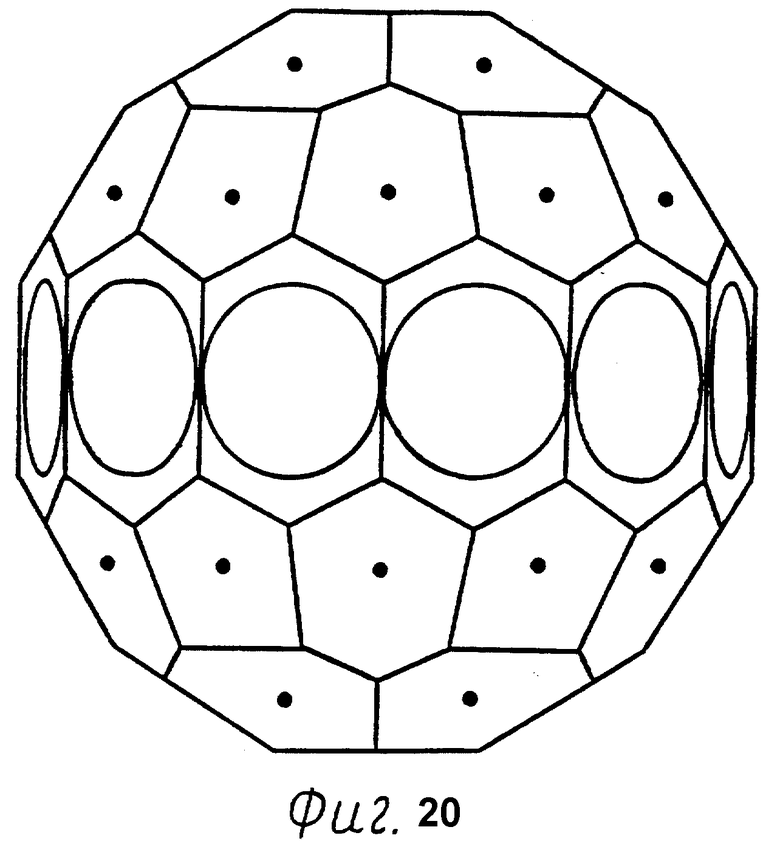
Фиг. 20 - точки касания и линии пересечения сферы диаметром, равным высоте конструкции с гранями. Точки касания эллипсоида с гранями.
Фиг. 21 - точки касания сверху на фиг. 20.
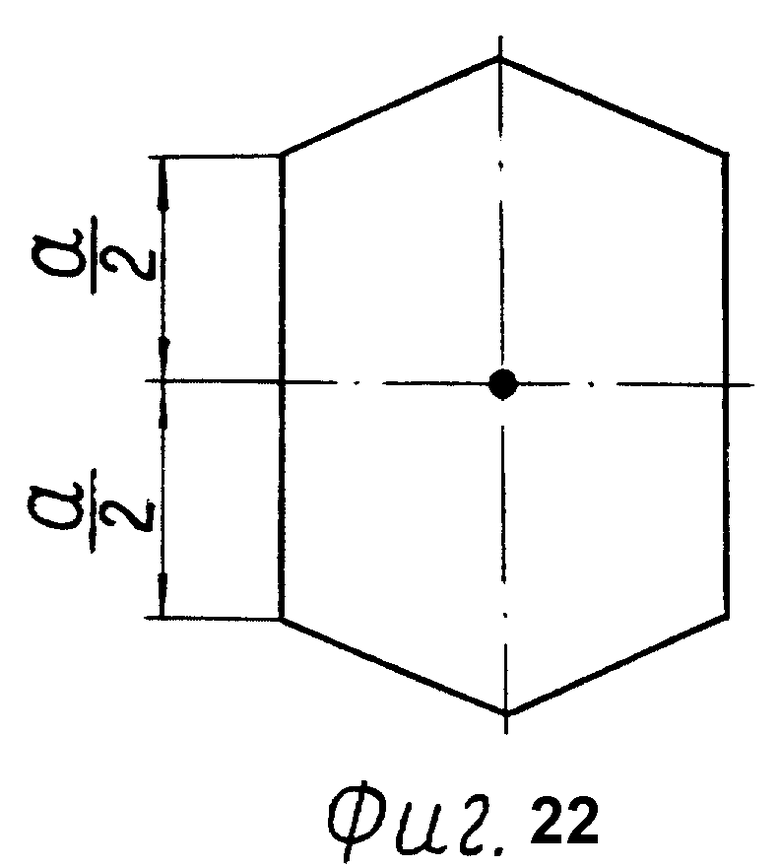
Фиг. 22 - 26 - центры тяжести граней.
Фиг. 27 - купол, изображение в диметрии. Рациональный вариант купола.
Фиг. 28 - купол, изображенный в диметрии. Второй вариант купола.
Фиг. 29 - увеличение объема конструкции.
| название | год | авторы | номер документа |
|---|---|---|---|
| СБОРНЫЙ СФЕРИЧЕСКИЙ КУПОЛ | 2017 |
|
RU2657553C1 |
| СПОСОБ ИЗГОТОВЛЕНИЯ ПОЛЫХ СФЕРИЧЕСКИХ ИЗДЕЛИЙ | 2001 |
|
RU2189268C2 |
| УЧЕБНОЕ ПОСОБИЕ ПО ГЕОМЕТРИИ В ВИДЕ МАКЕТА СКЛАДЫВАЕМОГО ТЕЛА | 1991 |
|
RU2023313C1 |
| ОБЪЕМНАЯ ЛОГИЧЕСКАЯ ГОЛОВОЛОМКА | 1992 |
|
RU2009678C1 |
| Сборная структура на основе сферического икосаэдра | 2023 |
|
RU2821229C1 |
| УСТРОЙСТВО ДЛЯ ТРЕХКООРДИНАТНЫХ ПЕРЕМЕЩЕНИЙ | 1999 |
|
RU2150169C1 |
| ОБЪЕМНЫЙ ЭЛЕМЕНТ ДЛЯ СОТОВЫХ КОНСТРУКЦИЙ И СПОСОБ ИЗГОТОВЛЕНИЯ ТРЕХСЛОЙНЫХ СОТОВЫХ КОНСТРУКЦИЙ С ЕГО УЧАСТИЕМ | 1994 |
|
RU2084349C1 |
| ШАРООБРАЗНАЯ ПРОСТРАНСТВЕННАЯ КОНСТРУКЦИЯ | 1995 |
|
RU2100539C1 |
| ОБЪЕМНЫЙ ЭЛЕМЕНТ И СПОСОБ ИЗГОТОВЛЕНИЯ СОТОВЫХ СТРУКТУР | 1993 |
|
RU2035313C1 |
| СИММЕТРИЧНЫЙ 32-ГРАННИК | 2004 |
|
RU2268080C1 |















Изобретение относится к строительству и предназначено для возведения сфероидальных куполов и конструкций. Технический результат заключается в увеличении прочности и устойчивости конструкции. Сфероидальная конструкция содержит 50 симметричных граней 5 типов. Верхним и нижним основаниями конструкции служат правильные шестиугольные грани. Конструкция состоит из 5 ярусов: экваториального пояса, содержащего 12 шестиугольных граней; двух одинаковых поясов, симметрично расположенных относительно экватора, каждый пояс содержит 6 шестиугольных граней и примыкает к основанию; двух одинаковых поясов, симметрично расположенных относительно экватора, каждый пояс содержит чередующиеся 6 пятиугольных и 6 шестиугольных граней и примыкает к экваториальному поясу. Прочность, общая устойчивость формы и пространственная жесткость конструкции обеспечивается тем, что конструкция имеет 4 плоскости симметрии, дающие при рассечении многогранника в сечениях правильные двенадцатиугольники, при этом все 96 вершин многогранника трехгранные. На основе сфероидальной конструкции можно получить 2 типа куполов. Элементы конструкции представлены в таком виде, который позволяет вычислить длины сторон и внутренние углы граней с любой степенью точности. 29 ил.
Многогранная сфероидальная конструкция, содержащая 50 симметричных граней 5 типов, отличающаяся тем, что конструкция имеет верхнее и нижнее правильные шестиугольные основания и состоит из 5 поясов: экваториального пояса, содержащего 12 шестиугольных граней; двух одинаковых поясов, симметрично расположенных относительно экватора, каждый пояс содержит 6 шестиугольных граней и примыкает к основанию; двух одинаковых поясов, симметрично расположенных относительно экватора, каждый пояс содержит чередующиеся 6 пятиугольных и 6 шестиугольных граней и примыкает к экваториальному поясу, при этом грани многогранника образуют 96 трехгранных вершин, а при рассечении многогранника 4 плоскостями симметрии, 3 плоскостями проходящими через середины стороны правильных шестиугольных оснований и одной плоскостью, проходящей через экватор, в сечениях получаются правильные двенадцатиугольники.
| В мире науки, 1989, N 11, с | |||
| Аппарат для радиометрической съемки | 1922 |
|
SU124A1 |
| US 4679361 A, 14.07.87 | |||
| US 4825602 A, 02.05.89 | |||
| Сборная сферическая оболочка | 1986 |
|
SU1321794A1 |
| Рюле Г | |||
| Пространственные конструкции | |||
| - М.: Стройиздат, 1974, с | |||
| Устройство для выпрямления опрокинувшихся на бок и затонувших у берега судов | 1922 |
|
SU85A1 |
| US 4309852 A, 12.01.82 | |||
| КУПОЛЬНОЕ ПОКРЫТИЕ | 1992 |
|
RU2035561C1 |
Авторы
Даты
1998-11-20—Публикация
1996-12-11—Подача