Изобретение относится к области измерительной техники и может быть использовано в случае измерения сигналов произвольной формы /широкополосных/ в присутствии больших случайных шумов, т.е. при отношении S/N ≤ 1,0.
Широко известным способом измерения сигналов произвольной формы в присутствии случайных шумов является спектральный метод, описанный в [1, 2]. В [1] используется цифровой фильтр, основанный на дискретном преобразовании Фурье, в [2] применен способ апостериорной "Винеровской фильтрации", основанный на прямом и обратном преобразовании Фурье. При "Винеровской фильтрации" определяется исправленное преобразование Фурье, получают "отфильтрованную по Винеру" кривую.
Спектральные методы позволяют получить результат только в апостериорном режиме, т.е. требуют больших временных затрат.
Известен также способ согласованной фильтрации [3], основанный на перемножении на сигнал известной формы с последующим когерентным накоплением результатов измерения. Число накоплений при согласованной фильтрации в 2-3 раза меньше по сравнению с обычным способом когерентного накопления. Эффективность согласованной фильтрации уменьшается с уменьшением отношения сигнал/шум на входе.
Недостатком данного способа является необходимость определения формы сигнала либо форма сигнала и его длительность должны быть известны заранее. В тех случаях, когда форма измеряемого сигнала информативна, т.е. зависит от состояния исследуемого объекта, метод согласованной фильтрации требует дополнительных временных затрат для определения формы измеряемого сигнала, сто снижает его быстродействие.
Известны способы и устройства [4, 5, 6], позволяющие связать параметры детерминированных сигналов /значение постоянного напряжения, амплитуду и среднеквадратическое значение переменных сигналов произвольной формы/ с начальной фазой первой гармоники искусственно сформированного гармонического ступенчатого сигнала, в котором сначала формируют первый импульсный сигнал, амплитуда которого равна сигналу делителя, а длительность равна третьей части периода, затем формируют второй импульсный сигнал, амплитуда которого равна сигналу делимого, а длительность равна третьей части периода, преобразуют периодический ступенчатый импульсный сигнал в гармонический, фаза которого измеряется фазоизмерительной схемой и пропорциональна результату деления двух импульсных напряжений. При известном сигнале-делителе данный способ можно рассматривать как способ измерения значения сигнала-делимого.
Однако в способах и устройствах [4, 5, 6] не рассматривается воздействие помехи на фазу информативной гармоники, в [6] сигнал и помеха подвергаются однополупериодному выпрямлению. При таком преобразовании помехи математическое ожидание ее на периоде информативной гармоники T не равно нулю и поэтому помеха сдвигает начальную фазу информативной гармоники так же, как и полезный сигнал.
Кроме того, способы [4, 5, 6] позволяют измерить только отдельные параметры физических процессов, которые за время измерения являются постоянными /значение постоянного напряжения, амплитуда переменного сигнала, среднеквадратическое значение переменных сигналов произвольной формы/.
Наиболее близким по достигаемому результату является способ когерентного накопления сигнала и шума [7]. Сущность данного способа основана на том, что сигнал с помехой поступают на входной полосовой фильтр, нижняя и верхняя граничная частоты которого определяются минимальными искажениями формы измеряемого сигнала произвольной формы, нижняя граничная частота fгр.Н - медленными компонентами сигнала, верхняя граничная частота fгр.В - быстрыми компонентами, причем расширение полосы пропускания фильтра приводит к ухудшению отношения сигнал/шум - S/Nвых. Далее сигнал с шумом на выходе полосового фильтра подвергают дискретизации с шагом Δtg = 1/2fгр.в /по теореме Шеннона [8]/ и квантованию по уровню, полученные дискретные значения когерентно суммируют, т. е. суммируют значения сигнала, находящиеся в постоянном временном соотношении к некоторому событию, вызвавшему данный сигнал.
Отношение сигнал/шум в методе когерентного накопления улучшается в 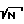 раз, где N - число реализаций.
раз, где N - число реализаций.
Основными недостатками способа когерентного накопления являются:
1. Ограничение частотного диапазона входного сигнала снизу и сверху с помощью входного полосового фильтра, что приводит заведомо к искажению медленных и быстроменяющихся составляющих сигнала и снижению точности воспроизведения формы измеряемого сигнала произвольной формы по результатам измерения данным методом.
2. Метод когерентного накопления является линейным и поэтому улучшения отношения сигнал/шум на выходе можно получить только путем увеличения числа реализаций N и, соответственно, времени измерения, поэтому данный метод при фиксированном времени измерения имеет определенную помехоустойчивость, которую можно увеличить только за счет увеличения времени либо уменьшения полосы пропускания входного фильтра, то есть искажения входного сигнала.
3. В методе когерентного накопления используется текущее мгновенное значение сигнала и помехи в одной точке на i-м шаге дискретизации Δtgi, информация о сигнале и помехах вне этой точки на i-м шаге дискретизации не используется.
4. Ограниченный динамический диапазон и чувствительность.
Целью предлагаемого изобретения является измерение сигнала произвольной формы в присутствии случайных шумов с более высокой точностью, быстродействием, помехоустойчивостью, чувствительностью и более широким динамическим диапазоном.
Поставленная цель достигается тем, что в способе измерения сигналов произвольной формы в присутствии случайных шумов сигнал с помехой подвергают дискретизации и когерентному накоплению, формируют постоянные опорные напряжения U1= и U2=, суммируют опорное напряжение U2= с измеряемым сигналом Ux(t) с помехой n(t) и дополнительным шумом N(t), причем сумма шумов n(t)+N(t) представляет широкополосный равномерный по частоте шум с полосой от 0 до fв.п., закон распределения которого определяется законом распределения шума n(t), fв.п. - верхняя частота полосового шума, которую выбирают исходя из заданной точности, быстродействия и помехоустойчивости, осуществляют перемножение со сдвигом во времени, равным TИ1/2, опорного напряжения U1= и суммарного напряжения U2=+Ux(t)+n(t)+N(t) на последовательности прямоугольных импульсов длительностью TИ1/2, синхронизированных с частотой сигнала, следующих с частотой f1=1/T1, величина которой не менее (20-50)fв.п., причем импульс с амплитудой U1= опережает импульс с амплитудой U2=+Ux(t)+n(t)+N(t) на величину TИ1/2, формируют последовательность однополярных ступенчатых импульсов U1Σступ(t) длительностью TИ1, состоящих из первого импульса с амплитудой U1= и второго импульса с амплитудой, определяемой суммой U2=+Ux(t)+n(t)+N(t) на данном текущем периоде T1, равном M1TИ1, где M1=T1/TИ1, периодические ступенчатые импульсы преобразуют в гармонические путем узкополосной фильтрации с помощью избирательного фильтра на каждом интервале измерения T1, частота фильтра fф1=f1, параметры M1=T1/TИ1, D1=U2=/U1= и добротность фильтра Q1 выбирают исходя из получения необходимой чувствительности, линейности функции преобразования, точности, быстродействия и помехоустойчивости, текущие значения фазы информативной гармоники на периоде T1, пропорциональные Ux(t), следующие с частотой f1, преобразуют в длительности прямоугольных импульсов τi1 с частотой f1, амплитудой U22, формируют последовательность опорных однополярных прямоугольных импульсов длительностью τ1 = T1/2 с амплитудой U12 и частотой f1, сдвинутые на время T1/2 по отношению к импульсам с амплитудой U22, синхронизированные с частотой сигнала Ux(t), перемножают последовательности импульсов с частотой f1 и амплитудами U12 и U22 на последовательности прямоугольных импульсов с частотой f2=1/{[2(2N2-1)+2m2]•T1/2}, где N2 и m2 - целые числа, таким образом, что импульс, состоящий из прямоугольных импульсов с амплитудой U12 и частотой f1 опережает на время TИ2/2=(2N2-1)T1/2 импульс, состоящий из прямоугольных импульсов с амплитудой U22 с частотой f1, формируют последовательность однополярных ступенчатых импульсов U2Σступ(t), следующих с частотой f2, состоящих из первого импульса, представляющего последовательность однополярных прямоугольных импульсов с амплитудой U12 и длительностью TИ2/2= (2N2-1)•T1/2, и второго импульса, представляющего последовательность однополярных прямоугольных импульсов с амплитудой U22, длительностью TИ2/2= (2N2-1)•T1/2, причем длительность каждого импульса τi1 с амплитудой U22 пропорциональна фазе на каждом периоде измерения T1, параметры M2=T2/TИ2= (2N2-1+m2)/(2N2-1), D2=U22/U12, периодические ступенчатые импульсы преобразуют в гармонические путем узкополосной фильтрации с помощью избирательного фильтра на каждом интервале измерения T2, частота фильтра fф2=f2, параметры M2, D2, добротность фильтра Q2 выбирают исходя из необходимой чувствительности, линейности функции преобразования, точности, быстродействия и помехоустойчивости, причем формирование однополярных ступенчатых импульсов осуществляют многократно с понижением частоты следования импульсов до достижения равенства Tn = Δtg = 1/2fгр.в, где fгр.в - верхняя граничная частота в спектре сигнала по теореме Шеннона, полученные значения фазы информативной гармоники на периоде Tn, пропорциональные текущему значению измеряемого сигнала Ux(t), вводят в блок памяти, вывод результатов измерения из которого осуществляют под контролем блока управления, регистрируют данные на принтере.
При недостаточном отношении сигнал/шум повторяют измерение необходимое количество раз и результаты измерений когерентно суммируют.
Существенными отличительными признаками предлагаемого способа являются: суммирование на входе измеряемого напряжения Ux(t) с помехой n(t) с постоянным опорным напряжением U2= и дополнительным шумом N(t), с помощью которого получают сумму шумов /n(t)+N(t)/ в виде равномерного по частоте широкополосного шума от 0 до fв.п с законом распределения шума n(t); многократное формирование последовательности однополярных ступенчатых импульсов с заданным отношением уровней напряжений D1, D2, ..., длительностью M1 = TИ1/T1, M2 = T2/TИ2, ..., с увеличивающимся периодом следования T1<T2<... <Ti<...<Tn, где f1=1/T1≥(20-50)fв.п, конечное значение периода Tn = Δtg = 1/2fгр.в, fгр.в - верхняя граничная частота в спектре сигнала, промежуточное преобразование текущего значения фазы в длительности импульсов τii, следующих с частотой fi-1; синхронизация начального момента преобразования с моментом подачи входного измеряемого сигнала Ux(t).
Сущность предлагаемого способа в отличие от прототипа заключается в том, что расширяют спектральный состав помехи на входе от 0 до fв.п, где fв.п - верхняя граничная частота полосового шума, вводя в состав шума дополнительные спектральные составляющие для получения равномерно распределенного по частоте шума в полосе частот от 0 до fв.п, причем с увеличением fв.п увеличивается частота изменения во времени напряжения полосового шума, амплитуда шума, частота переходов через нулевые значения; измеряемый сигнал Ux(t) с шумом /n(t)+N(t)/ преобразуют в фазу информативной гармоники искусственно сформированного ступенчатого импульса с частотой f1=1/T1≥(20-50)fв.п, причем измеряемое напряжение сдвигает прямо пропорционально постоянное значение фазы на величину Δϕ
Формируют однополярные ступенчатые импульсы из последовательностей прямоугольных импульсов U12(t) и U22(t), следующие с частотой f2=1/T2. Фаза информативной гармоники ϕ2Σступ(t) с периодом T2 зависит прямо пропорционально от Δϕx = f[Ux(t)], случайные изменения фазы ±Δϕi1n(t) и, соответственно, изменения длительности импульсов ±Δτi1n(t) на периоде T2 приводят к частотной модуляции информативной гармоники с периодом T2 и соответственно к расширению спектра и нелинейному преобразованию амплитуд составляющих спектра.
Индекс частотной модуляции зависит от параметра M2 и значений ±Δϕi1n(t). Часть спектральных составляющих устраняется фильтром с добротностью Q2 и частотой fф = f2.
Нелинейные преобразования сигнала с шумом продолжают до тех пор, пока fфп = fд, где fд - частота дискретизации по теореме Шеннона fg = 1/Δtg = 2fгр.в, с целью достижения необходимой точности, быстродействия, помехоустойчивости, чувствительности и линейности функции преобразования.
Параметры D1, D2, ..., Di, ..., Dn; M1, M2, ..., Mi, ..., Mn задают с целью получения линейной зависимости измеряемого сигнала с фазой информативной гармоники, получения высокой чувствительности к измеряемому напряжению и помехоустойчивостью.
В проанализированной патентной и научно-технической литературе данная совокупность существенных признаков не найдена, которая приводит к достижению нового положительного эффекта, а именно измерению сигналов произвольной формы в присутствии случайных шумов с высокой точностью, быстродействием, помехоустойчивостью, чувствительностью и широким динамическим диапазоном.
Таким образом, данное предложение соответствует критериям "новизна" и "существенные отличия".
На фиг. 1 показано устройство, реализующее данный способ; на фиг. 2 - временные диаграммы, поясняющие осуществление способа.
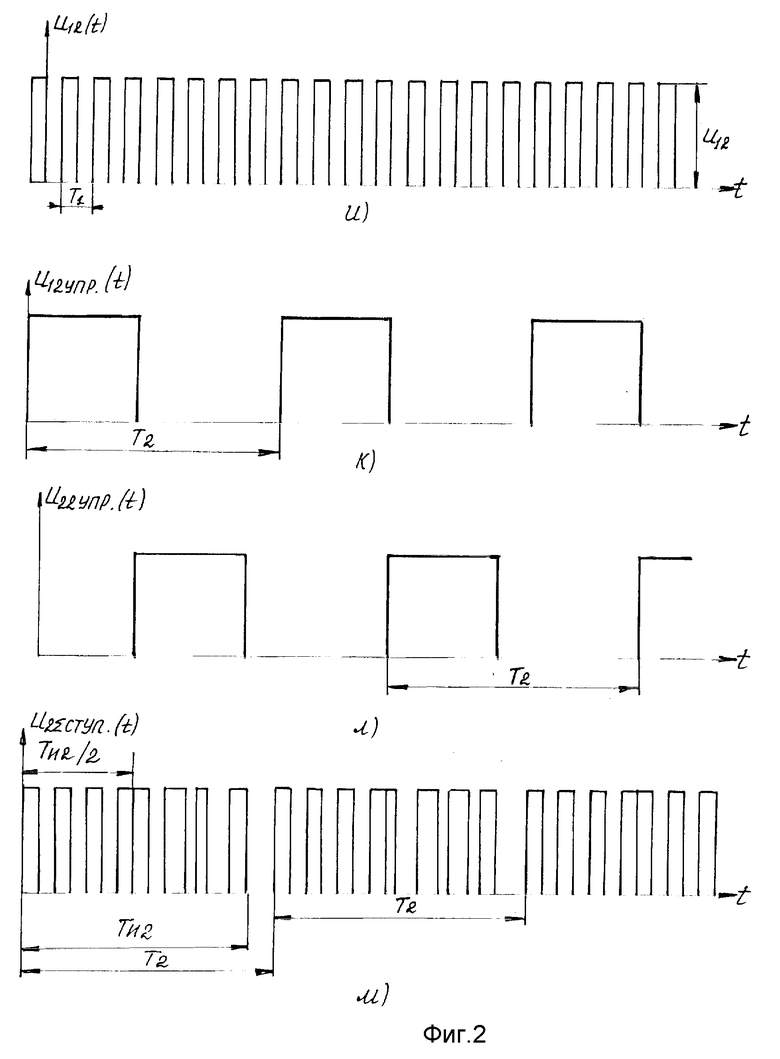
Устройство измерения сигналов произвольной формы в присутствии случайных шумов, фиг. 1, реализующее данный способ, состоит из сумматора 1, кнопки 2 "Пуск", блока 3 управления, сумматора 4, ключей 51, 52, ..., 5i, ..., 5n, 61, 62, ..., 6i, ..., 6n, формирователей 71, 72, ..., 7i, ..., 7n, ступенчатых импульсов, избирательных усилителей 81, 82, ..., 8i, ..., 8n, фазовращателей 91, 92, ..., 9i, ..., 9n, преобразователей 101, 102, ..., 10i, ... , 10n-1 фазы в длительности τii прямоугольных импульсов, фазометра 11, памяти 12, блока 13 управляемой выборки, переключателя П на две позиции, преобразователя 14 код-аналог, сумматора 15, регистратора 16.
Выход сумматора 1 соединен со входом кнопки 2 "Пуск", выходы кнопки 2 "Пуск" соединены со входами блока 3 управления и первым входом сумматора 4. Сигнальный выход блока 3 управления соединен со вторым входом сумматора 4. Выход сумматора 4 подключен через ключ 5 к первому входу формирователя 7 ступенчатых импульсов, сигнальный выход блока 3 управления подключен через ключ 6 ко второму входу формирователя 7 ступенчатых импульсов. Выходы преобразователей 101, 102, ..., 10i, ..., 10n-1 фазы в длительности τii прямоугольных импульсов соединены с первыми входами формирователей 72, ..., 7i, .. . , 7n ступенчатых импульсов через ключи 52, ..., 5i, ..., 5n. Сигнальные выходы блока 3 управления подключены через ключи 62, ..., 6i, ..., 6n ко вторым входам формирователей 72, ..., 7i, ..., 7n ступенчатых импульсов. Выходы блока 3 управления, осуществляющие синхронизацию работы устройства, подключены соответственно ко вторым входам блоков 51, 52, ..., 5i, ..., 5n, 61, 62, ..., 6i, ..., 6n, 11, 12, 13.
Предлагаемый способ реализуется следующим образом. Сигнал Ux(t) с помехой n(t) поступает на первый вход сумматора 1, на второй вход которого поступает дополнительный шум N(t) от внешнего источника случайного шума. Сумма шумов /n(t)+N(t)/ имеет равномерный спектр по частоте и закон распределения, определяемый законом распределения шума n(t). Суммарное напряжение /Ux(t)+N(t)+n(t)/ поступает через кнопку 2 "Пуск", на первый вход сумматора 4, на второй вход которого поступает постоянное опорное напряжение U1= по сигналу из кнопки 2 "Пуск" в блок 3 управления, выходное напряжение сумматора 4 /U2=+Ux(t)+n(t)+N(t)/ представлено на фиг. 2г.
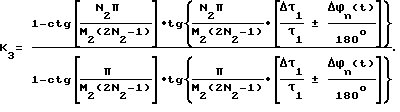
Управляющие импульсы UУПР.1(t) и UУПР.2(t), следующие с частотой f1 = 1/T1, сдвинутые на TИ1/2 относительно друг друга, синхронизированные с частотой сигнала, поступают на вторые входы ключей 51, 61, на первые входы которых поступают сумма /U2=+Ux(t)+n(t)+N(t)/ и постоянное опорное напряжение U1= соответственно. На формирователе 71 формируется последовательность ступенчатых импульсов U1Σступ(t) длительностью TИ1 с частотой f1=1/T1, фиг. 2е. Избирательный усилитель 81 с добротностью Q1 выбирает первую гармонику с частотой f1, фазу которой ϕ1Σступ(t), фиг. 2ж, в блоке 101 преобразуют в длительности τi1 = τ1+Δτi1n(t) последовательности прямоугольных импульсов U22(t), фиг. 2з.
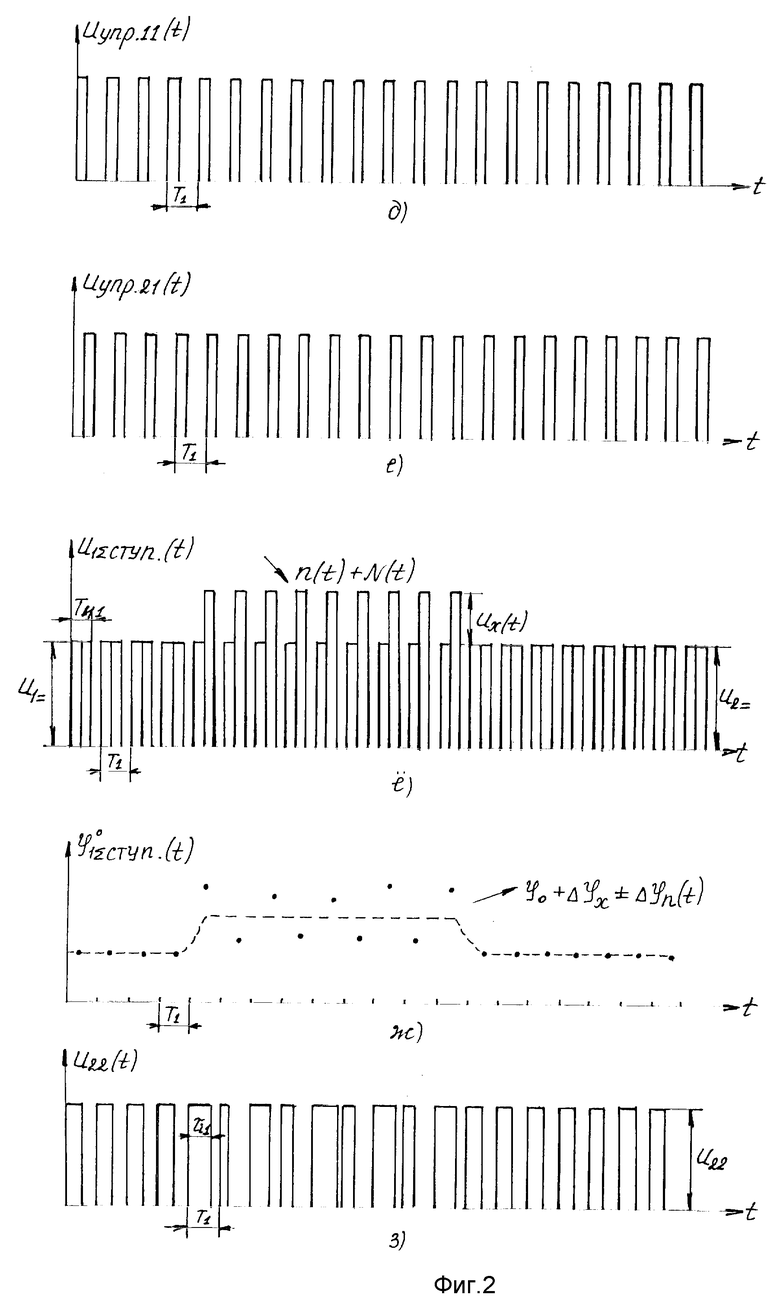
В блоке 3 управления формируют опорную последовательность импульсов U12(t) длительностью τ1, следующую с частотой f1, опережающую последовательность U22(t) на время TИ1/2 /на фиг. 2 и τ1 = M1TИ1/2 = T1/2/. Управляющие импульсы UУПР.12(t) и UУПР.22(t) поступают из блока 3 управления на вторые входы ключей 52, 62, на первые входы которых поступают последовательности импульсов U12(t) и U22(t) соответственно. На выходе формирователя 72 формируется последовательность однополярных ступенчатых импульсов U2Σступ(t) длительностью TИ2=/2N2-1/T1, следующих с периодом T2=[/2N2-1/+m2] T1, где N2 и m2 - целые числа, m2 может быть равным 0.
Избирательный усилитель 82 с добротностью Q2 выбирает первую гармонику с частотой f2 = 1/T2, фазу которой ϕ2Σступ(t) преобразуют в блоке 102 в длительности τi2 прямоугольных импульсов, следующих с частотой f2. Таким образом осуществляется преобразование амплитуды сигнала и шума в фазу, а затем фазы в фазу. Преобразование "фаза-фаза" осуществляется до тех пор, пока период информативной гармоники не станет равным шагу дискретизации по теореме Шеннона Δtg = Tn.
Количество преобразований определяется точностью, быстродействием, помехоустойчивостью, динамическим диапазоном сигнала и помехи, чувствительностью и линейностью функции преобразования.
Текущее i-е значение периода равно:
Ti=[(2Ni-1)+mi]•Ti-1, (1)
где Ni = 1, 2, 3, ...; mi = 0, 1, 2, 3, ...; i = 1, 2, 3, ..., n.
Конечное значение периода равно:
Tn = [(2Nn-1)+mn]•Tn-1. (2)
Сигнал с выхода избирательного усилителя 8n через фазовращатель 9n поступает на фазометр 11 и затем в блок 12 памяти под контролем блока 3 управления.
С помощью блока 13 управляемой выборки из блока 12 памяти в той же последовательности в реальном масштабе времени выводятся текущие значения фазы ϕnΣступ(t)/ через переключатель П непосредственно на преобразователь 14 код-аналог либо через сумматор 15 в том случае, когда отношение сигнал/шум на выходе является недостаточным.
С выхода преобразователя 14 сигналы поступают на регистратор 16.
Для обоснования предлагаемого способа измерения сигналов произвольной формы в присутствии случайных шумов найдем выражение, связывающее фазу информативной гармоники с измеряемым напряжением Ux(t) и суммой шумов /n(t)+N(t)/, которое получается на основании преобразования Фурье однополярного ступенчатого импульса U1Σступ(t):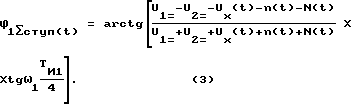
Обозначим:
n(t)+N(t) = nΣ(t);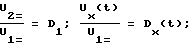
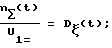
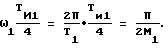
Тогда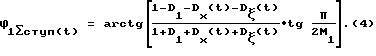 (4)
(4)
Значение информативной гармоники U1(t) равно: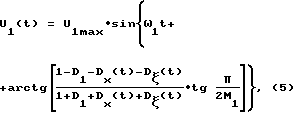
где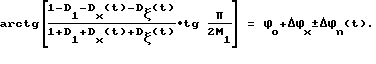
Выражение для фазы ϕ2Σступ(t), полученное на основании преобразования Фурье однополярного ступенчатого импульса U2Σступ(t), фиг. 2м, для случая +Δτ1 имеет вид: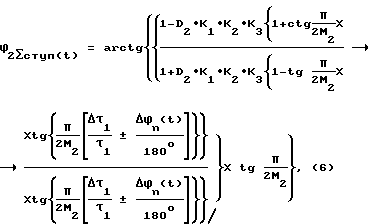
где D2 = U22/U12;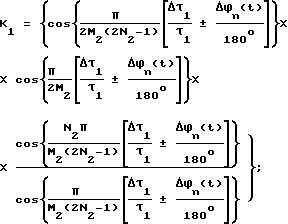
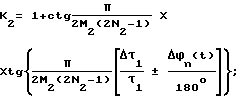
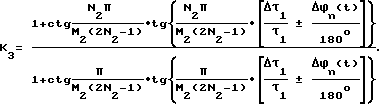
Выражение для случая /-Δτ1/ имеет вид: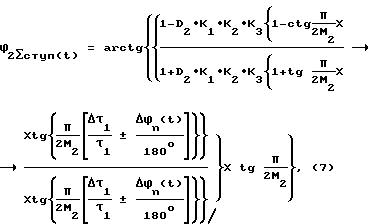
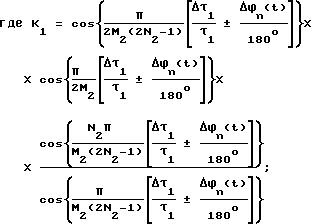
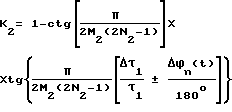
Значения информативной гармоники U2(t) и U3(t) равны соответственно: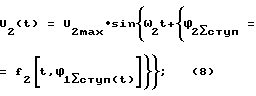
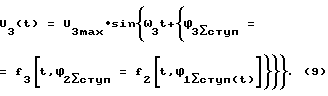
Текущее значение информативной гармоники Ui(t) равно:
Значение n-й информативной гармоники с периодом Tn = Δtg равно: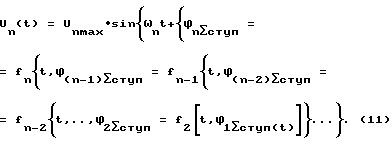
Анализ полученных выражений показал, что сигнал Ux(t), когерентный с опорными сигналами, приводит к пропорциональному изменению постоянной фазы информативных гармоник на величину Δϕx, а полосовая помеха nΣ(t) приводит к динамическим случайным изменениями фазы ±Δϕni(t) относительно постоянного значения и соответственно к частотной модуляции значений информативных гармоник в соответствии с выражениями /5/, /8/, /9/, /10/, /11/.
Глубина частотной модуляции зависит от параметров M1, M2, ..., Mi, ..., Mn, D1, D2, . . . , Di, ..., Dn, от величины амплитуды помехи nΣ(t) и ее верхней частоты fв.п.
Выходные фильтры с добротностями Q1, Q2, ..., Qi, ..., Qn при каждом нелинейном преобразовании уменьшают энергию помехи за счет устранения боковых спектральных составляющих без увеличения времени благодаря нелинейному преобразованию значений U(t) и ϕ(t) помехи на интервалах TИi/2, сигнал, когерентный с опорным напряжением, проходит на выход без искажения, т.к. носителем сигнала являются постоянные фазы информативных гармоник с частотами, являющимися центральными частотами избирательных усилителей.
Если при нелинейном преобразовании сигнала с помехой не достигается необходимое для измерения отношение сигнал/шум, то возможно обычное когерентное накопление значений фаз в сумматоре 15.
Анализ литературных источников [9, 10] показал следующее.
1. Существует теория, основанная на функциях Бесселя 1-го рода n-го порядка, описывающая амплитудный спектр синусоидального сигнала, модулированного по частоте либо по фазе синусоидальной модулирующей функцией; модулированного по нескольким частотам, когда модуляция наложена суммой некоторого числа синусоидальных функций, когда между соответствующими круговыми частотами существуют простые линейные соотношения; модулированного суммой синусоидальных функций, круговые частоты которых находятся в простом соотношении, в частности, в случае модуляции периодическим сигналом, разложенным в ряд Фурье.
2. Отсутствуют теоретические исследования фазового спектра синусоидального сигнала, модулированного по частоте либо по фазе.
В данном способе модулирующей функцией является напряжение помехи nΣ(t) на интервале TИ1/2 либо случайные изменения длительностей импульсов Δτii на интервалах TИ2/2, TИ3/2, ..., TИi/2, ..., TИn/2, поэтому теоретически индекс частотной модуляции определить невозможно, можно только говорить о максимальных частотных и фазовых отклонениях при модуляции, которые могут иметь разные значения справа и слева от средней частоты.
Поэтому автором предлагаемого способа выбран экспериментальный путь исследований фазы ϕiΣступ(t) при воздействии различных помех /синусоидальная, полосовые с различными законами распределения/.
Результаты экспериментальных исследований, подтверждающие достижение положительного эффекта предлагаемым способом, представлены в приложении.
На основании проведенных исследований можно сделать следующие выводы.
1. В предлагаемом способе повышается точность измерения сигналов произвольной формы за счет расширения полосы пропускания от 0 до fгр.в, где fгр.в - верхняя граничная частота в спектре сигнала по теории Шеннона, а также за счет использования информации о сигнале с помехой на интервале от TИi/2 до TИi, а не в точке и уменьшения времени переходных процессов по фазе выходных фильтров.
2. Быстродействие предлагаемого способа значительно больше прототипа за счет нелинейного преобразования сигнала с помехой, в результате которого результат /среднее значение фазы/ достигается значительно быстрее, причем увеличение верхней частоты полосовой помехи fв.п независимо от закона ее распределения приводит к более быстрым изменениям фазы ±Δϕn(t) относительно постоянной фазы информативной гармоники искусственно сформированного импульса и к более быстрому ее осреднению.
3. Одновременно при высоком быстродействии достигается большая помехоустойчивость, т. к. сигнал усиливается прямо пропорционально, а помеха подвергается нелинейному преобразованию, спектр помехи расширяется при каждом i-м преобразовании, боковые компоненты устраняются выходными полосовыми фильтрами, что приводит к повышению сигнал/шум на выходе. Кроме того, значения δϕ и Mϕ не возрастают прямо пропорционально мощности шума, а в ряде случаев вообще не изменяются с увеличением мощности шума, что доказано экспериментально.
4. Путем соответствующего выбора верхней частоты полосовой помехи при заданном законе распределения шума n(t), частоты преобразования f1 и последующих частот, количества преобразований "фаза-фаза" при данном значении fгр.в сигнала по теореме Шеннона, частотных полос фильтров, мощности шума Pш возможно выделение сигнала произвольной формы из шума в реальном масштабе времени, что доказано экспериментально.
5. Динамический диапазона преобразователя "амплитуда-фаза" бесконечен, необходимую чувствительность к измеряемому сигналу можно получить путем соответствующего выбора параметров M1, M2, ..., Mi, ..., Mn; D1, D2, ..., Di, ..., Dn и числа преобразований n с понижением периода от T1 до Tn = Δtg = 1/2fгр.в.
Таким образом, в предлагаемом способе сигнал приводит к постоянному изменению фазы информативной гармоники искусственно сформированного ступенчатого импульса, а полосовая помеха к динамическим изменениям фазы ±Δϕn(t) относительно постоянного значения, причем увеличение верхней частоты полосовой помехи приводит к более быстрым изменениям ±Δϕn(t) и соответственно ее быстрому осреднению, не приводя к пропорциональному увеличению среднеквадратических отклонений отдельного результата δϕ, среднеквадратического отклонения среднего 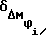 и средних значений фазы
и средних значений фазы 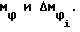
Источники информации:
1. Хечинашвили С.Н., Кеванишвили С.Ш. Коротколатентный слуховой вызванный потенциал человека. В кн.: Сенсорные системы. - Л.: Наука, 1982, с. 87-108.
2. Walter D.O., Braizier M.A. Advances in EEG analysis. - Electroenceph. Clin. Neurophysiol., 1968, vol. 27, p. 78.
3. Woodworth W., Riesman S.S., Fontaine A.B. The detection of auditory evoked responses using a matched filter. - IEEE Transactions on Biomedical Engineering, 1983, v. 8 ME-30, N 7.
4. Авторское свидетельство N 1104536, 1984.
5. Авторское свидетельство N 1247765, 1986.
6. Авторское свидетельство N 1179181, 1985.
7. Киреев А.М., Широков В.С., Шахнович А.Р., Белоусов О.Б., Москаленко Ю.Г. Методы и технические средства регистрации и обработки слуховых вызванных потенциалов мозга. - М.: ЦНТИ, 1985, вып. 4, 37 с.
8. Макс Ж. Методы и техника обработки сигналов при физических измерениях. - М.: Мир, 1983, т. 1, 311 с.
9. Анго Андре. Математика для электро- и радиоинженеров. - М.: Наука, 1967, с. 780.
10. Картьяну Г. Частотная модуляция. - Бухарест, Меридиане, 1964, с. 671.

Способ заключается в том, что сигнал с помехой подвергают дискретизации и когерентному накоплению, формируют постоянные опорные напряжения U1= и U2=, суммируют напряжение U2= с измеряемым сигналом Uх(t) с помехой n(t) и дополнительным шумом N(t), осуществляют перемножение со сдвигом во времени, формируют последовательность однополярных ступенчатых импульсов U1Σступ(t) длительностью Ти1, периодические ступенчатые импульсы преобразуют в гармонические путем узкополосной фильтрации, текущие значения фазы информативной гармоники на периоде Т1, пропорциональные Uх(t), следующие с частотой f1, преобразуют в длительности прямоугольных импульсов τi1 с частотой f1, амплитудой U22, формируют последовательность опорных однополярных прямоугольных импульсов длительностью τ1 = Т1 / 2 с амплитудой U12 и частотой f1, сдвинутые на время Т1/2 по отношению к импульсам с амплитудой U22, синхронизированные с частотой сигнала Uх(t), перемножают последовательности импульсов с частотой f1 и амплитудами U12 и U22 на последовательности прямоугольных импульсов с частотой f2, формируют последовательность ступенчатых импульсов U2Σступ(t), следующих с частотой f2, причем формирование однополярных ступенчатых импульсов осуществляют многократно с понижением частоты следования импульсов до достижения равенства Tn= Δtg= 1/2fгр.в, где fгр.в - верхняя граничная частота в спектре сигнала по теореме Шеннона, полученные значения фазы информативной гармоники на периоде Тn, пропорциональные текущему значению измеряемого сигнала Uх(t), вводят в блок памяти. Технический результат заключается в повышении точности, быстродействия, помехоустойчивости, чувствительности и расширении динамического диапазона. 1 з.п.ф-лы, 2 ил.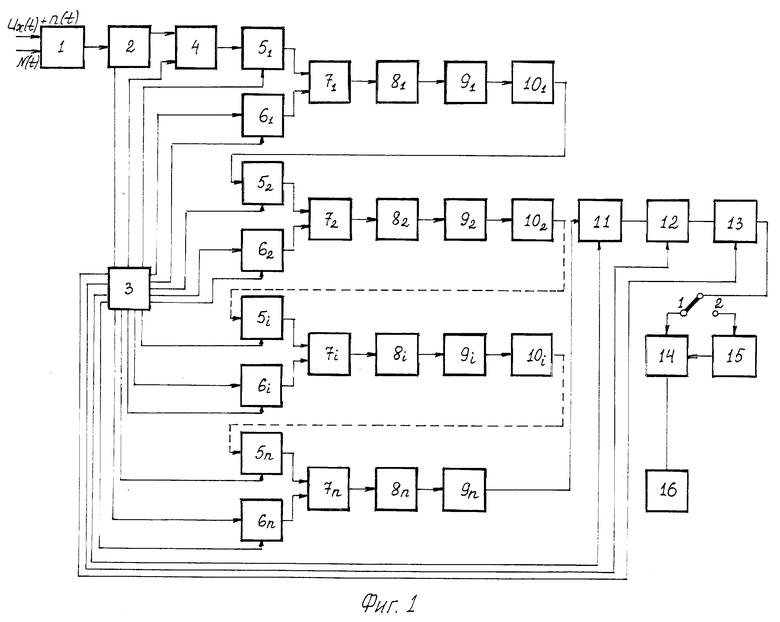
| Промышленность медицинской техники | |||
| Обзорная информация | |||
| Вып | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| Методы и технические средства регистрации и обработки слуховых вызванных потенциалов мозга | |||
| Приспособление для установки двигателя в топках с получающими возвратно-поступательное перемещение колосниками | 1917 |
|
SU1985A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Способ измерения среднеквадратического значения напряжения сложной формы | 1990 |
|
SU1829011A1 |
| Измерительный преобразователь электрических сигналов произвольной формы | 1988 |
|
SU1525605A1 |
| Способ измерения среднеквадратического значения напряжения сложной формы | 1989 |
|
SU1666962A1 |
| Измеритель эффективного значения периодических сигналов на фоне шума | 1987 |
|
SU1499248A1 |
| Способ измерения среднеквадратических значений напряжений произвольной формы и устройство для его осуществления | 1984 |
|
SU1247765A1 |
| Устройство для деления сигналов | 1984 |
|
SU1179381A1 |
| Жилинскас Р.П | |||
| Измерители отношений и их применение в радиоизмерительной технике | |||
| - М.: Сов.радио, 1975, с | |||
| Пишущая машина | 1922 |
|
SU37A1 |
Авторы
Даты
1999-07-20—Публикация
1997-10-30—Подача