Изобретение относится к учебным приборам по физике и может быть использовано в лабораторном практикуме в высших и средних специальных учебных заведениях по курсу физики для изучения и углубления знаний физических законов.
Для определения циркуляции вектора напряженности магнитного поля 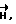 а также вектора напряженности электрического поля
а также вектора напряженности электрического поля 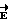 необходимо иметь источник поля и измеритель его в соответствующих точках конутра обхода.
необходимо иметь источник поля и измеритель его в соответствующих точках конутра обхода.
Известны устройства для создания и измерения электромагнитных полей, которые описаны в [1] , [2] и [3]. Известен также стенд для демонстрации свойств магнитного поля [4], в котором можно продемонстрировать различные свойства магнитного поля, однако, нельзя определить циркуляцию вектора 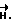
Известен способ демонстрации электрического поля [5]. На основе этого способа можно построить устройства для создания электрических полей в жидком прозрачном электролите. Однако, этот способ не предусматривает определения циркуляции вектора 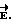
Из перечисленных литературных источников видно, что для создания магнитного или электрического поля, а затем определения циркуляции как вектора 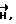 так и вектора
так и вектора 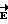 требуется сложное и дорогостоящее оборудование. Однако, сложные измерения в магнитном и электрическом поле можно заменить простым экспериментом, т.е. использовать математическое моделирование.
требуется сложное и дорогостоящее оборудование. Однако, сложные измерения в магнитном и электрическом поле можно заменить простым экспериментом, т.е. использовать математическое моделирование.
Наиболее близким к предлагаемому устройству является линейный потенциометр, который используется в цепи постоянного тока [6]. Сопротивление потенциометра при перемещении ползунка (подвижного контакта) будет меняться по линейному закону R = γr, где γ - коэффициент пропорциональности, а r - расстояние от начала потенциометра (неподвижного контакта) до ползунка. Это устройство позволяет моделировать только зависимость R=f(r), а не позволяет моделировать зависимость напряженности магнитного поля бесконечно длинного проводника с током, зависимость напряженности электрического поля точечного заряда, а также зависимость потенциала точечного заряда от расстояния до них. Следовательно, нельзя рассчитать циркуляцию вектора 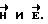
Целью изобретения является расширение функциональных возможностей известного устройства.
Эта цель достигается тем, что в существующее устройство введены: ключ; первый и второй неподвижный контакт; планшет с изображением контуров обхода; указатель точки на планшете, закрепленный на ползунке переменного резистора; высокий стержень, моделирующий бесконечный проводник с током и закрепленный перпендикулярно к планшету; шарик, насаженный на высокий стержень и моделирующий электрический точечный заряд; подвижная опора, на которой закреплен один конец переменного резистора; подвижная втулка, насаженная на высокий стержень и на которой закреплен другой конец переменного резистора; первый подвижный контакт, установленный на одном конце подвижной втулки; второй подвижный контакт, установленный на другом конце подвижной втулки; токопроводящий стержень, на котором перемещается ползунок переменного резистора, закрепленный одним концом с подвижной опорой, а другим концом соединен с вторым подвижным контактом; источник тока, соединенный минусовой клеммой через ключ, первый неподвижный контакт и первый подвижный контакт с неподвижным контактом переменного резистора; амперметр, соединенный одной клеммой с плюсовой клеммой источника тока, а второй клеммой через второй неподвижный контакт и второй подвижный контакт - с токопроводящим стержнем.
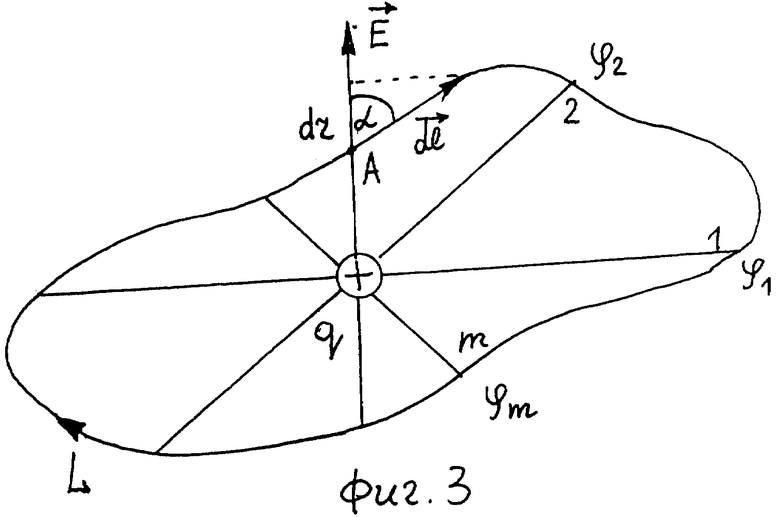
На фиг. 1, 2 и 3 представлены рисунки, поясняющие принцип работы предлагаемого устройства. На фиг. 4 изображен общий вид предлагаемого устройства.
Предлагаемое устройство (фиг. 4) содержит: 1 - ключ; 2 - источник тока; 3 - амперметр; 4 - второй неподвижный контакт; 5 - второй подвижный контакт; 6 - подвижная втулка; 7 - токопроводящий стержень; 8 - ползунок; 9 - переменный резистор; 10 - первый подвижный контакт; 11 - первый неподвижный контакт; 12 - высокий стержень, моделирующий бесконечный проводник с током; 13 - шарик, моделирующий электрический заряд; 14 - подвижная опора; 15 - указатель точки на планшете; 16 - планшет с изображением контуров обхода.
Зависимость напряженности магнитного поля H от расстояния r до проводника с током I описывается следующим выражением:
H = I/2πr (1)
Зависимость потенциала ϕ электрического поля E от расстояния r до точечного заряда q имеет вид
ϕ = q/4πεor, (2)
где εo - диэлектрическая постоянная.
Напряженность E электрического поля, создаваемого точечным зарядом, связана с потенциалом ϕ следующей зависимостью:
E = ϕ/r (3)
Зависимость сопротивления R от расстояния r до одного из неподвижных контактов переменного резистора (фиг. 1) имеет вид R = γr, где γ (Ом/м) - коэффициент пропорциональности. В свою очередь, ток J, протекающий под действием ЭДС источника тока ε через переменный резистор, зависит от переменного сопротивления R и соответственно от расстояния r.
J = ε/R = ε/γr (4)
Из выражений (1), (2) и (4) видно, что разные физические явления описываются одинаковыми математическими выражениями, т.е. имеют обратную пропорциональную зависимость H, ϕ и J от расстояния r. Поэтому в предлагаемом устройстве сложные явления создания и измерения магнитного и электрического поля заменяются простым устройством, моделирующим зависимость тока J от расстояния r.
Будем использовать выражение (4) в качестве математической модели выражений (1) и (2). Найдем взаимосвязь тока J, измеряемого амперметром A (фиг. 1), и моделируемой напряженности H магнитного поля. Для этого исключим параметр r из выражений (1) и (4), тогда получим
H = IγJ/2πε = K1J, (5)
где K1 = Iγ/2πε (1/м) - коэффициент пропорциональности.
Если положить K1= 1, то можно определить величину моделируемого тока в проводнике бесконечной длины l = 2πε/γ. В этом случае показания амперметра J (A) будут соответствовать величине напряженности магнитного поля H (А/м).
Таким образом, изменяя расстояние r от точки 0 (фиг.1), меняется сопротивление R переменного резистора, меняется ток J, измеряемый амперметром А, соответственно меняется по закону (5) и напряженность магнитного поля H. В конечном итоге с помощью переменного резистора (фиг. 1) моделируем зависимость напряженности магнитного поля H от расстояния r до проводника с током I, определяемую выражением (1).
Переменный резистор (фиг. 1) можно применить также для моделирования зависимости (2). Исключив из выражений (2) и (4) параметр r, получим взаимосвязь тока J, измеряемого амперметром А, и моделируемого потенциала ϕ электрического поля точечного заряда q, тогда получим
ϕ = (qγ/4πεoε)J = K2J, (6)
где K2= qγ/4πεoε (Ом) - коэффициент пропорциональности.
Если положить K2=1, то можно определить величину моделируемого точечного заряда q = 4πεoε/γ. В этом случае показание амперметра будет соответствовать величине потенциала ϕ (в).
Изменяя расстояние r от точки 0 (фиг. 1), меняется сопротивление R переменного резистора, меняется ток J, измеряемый амперметром А, соответственно меняется по закону (6) потенциал электростатического поля ϕ. Таким образом, с помощью переменного резистора (фиг. 1) моделируем зависимость потенциала ϕ от расстояния r, определяемую выражением (2).
Так как напряженность E и потенциал ϕ электростатического поля связаны зависимостью (3), то на данной модели можно также моделировать зависимость напряженности E электрического поля от расстояния до точечного заряда q.
Рассмотрим каким образом в данном устройстве определяется циркуляция вектора  по произвольному замкнутому контуру L. В точке А (фиг. 2) контура обхода L вектор
по произвольному замкнутому контуру L. В точке А (фиг. 2) контура обхода L вектор  направлен по касательной к магнитной силовой линии (изображена пунктирной линией) и, соответственно, перпендикулярен радиус-вектору
направлен по касательной к магнитной силовой линии (изображена пунктирной линией) и, соответственно, перпендикулярен радиус-вектору 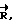 проведенному из точки 0, где расположен бесконечный проводник с током I. Ток I направлен перпендикулярно рисунку к нам.
проведенному из точки 0, где расположен бесконечный проводник с током I. Ток I направлен перпендикулярно рисунку к нам.
Вектор элемента контура 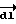 направлен из точки А по направлению обхода контура L. На фиг. 2 видно, что проекция
направлен из точки А по направлению обхода контура L. На фиг. 2 видно, что проекция 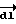 на направление
на направление  равна dS = dL cos α, где α - угол между векторами
равна dS = dL cos α, где α - угол между векторами 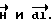 С другой стороны dS = Rdϕ, где dϕ - центральный угол, под которым виден элемент
С другой стороны dS = Rdϕ, где dϕ - центральный угол, под которым виден элемент 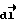 контура из точки 0, тогда dl cos α = Rd ϕ. С учетом этого выражение циркуляции вектора
контура из точки 0, тогда dl cos α = Rd ϕ. С учетом этого выражение циркуляции вектора  имеет вид:
имеет вид: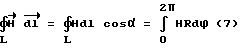
Если интервал углов от 0 до 2π разбить на конечное число m равных углов Δϕ = 2π/m, то интеграл (7) можно заменить суммой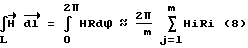
Из выражения (8) следует, что для определения циркуляции вектора  по произвольному контуру L необходимо разбить интервал углов от 0 до 2π на m равных углов Δϕ из радиусов, исходящих из точки 0 (фиг. 2). В каждой i-ой точке контура L измерить напряженность магнитного поля Hi, а также соответствующий радиус Ri, проведенный в i-ю точку из точки 0. Вычислить сумму произведений HiRi, а затем умножить на 2π/m.
по произвольному контуру L необходимо разбить интервал углов от 0 до 2π на m равных углов Δϕ из радиусов, исходящих из точки 0 (фиг. 2). В каждой i-ой точке контура L измерить напряженность магнитного поля Hi, а также соответствующий радиус Ri, проведенный в i-ю точку из точки 0. Вычислить сумму произведений HiRi, а затем умножить на 2π/m.
Циркуляция вектора 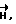 вычисленная по формуле (8), с высокой точностью совпадает со значением, которое можно получить по теоретической формуле
вычисленная по формуле (8), с высокой точностью совпадает со значением, которое можно получить по теоретической формуле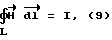
где I - моделируемый ток, протекающий по бесконечно длинному проводнику.
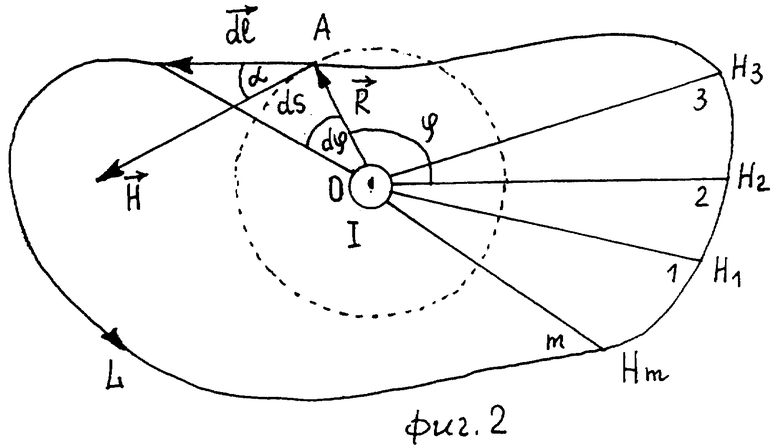
Рассмотрим, каким образом определяется циркуляция вектора 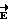 по произвольному замкнутому контуру L. В точке А (фиг. 3) контура L вектор
по произвольному замкнутому контуру L. В точке А (фиг. 3) контура L вектор 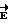 направлен по силовой линии и исходит из положительного точечного электрического заряда q. Вектор элемента контура обхода
направлен по силовой линии и исходит из положительного точечного электрического заряда q. Вектор элемента контура обхода 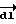 направлен из точки А по направлению обхода контура L. На фиг. 3 видно, что проекция
направлен из точки А по направлению обхода контура L. На фиг. 3 видно, что проекция 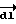 на направление вектора
на направление вектора 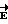 равна dr = dl cosα, где α - угол между векторами
равна dr = dl cosα, где α - угол между векторами 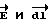 . Учитывая выражение (3) для бесконечно малого приращения расстояния dr, получим бесконечно малое приращение потенциала dϕ = Edr, тогда циркуляция вектора
. Учитывая выражение (3) для бесконечно малого приращения расстояния dr, получим бесконечно малое приращение потенциала dϕ = Edr, тогда циркуляция вектора 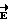 имеет вид:
имеет вид: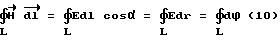
Проведем из центра расположения точечного заряда q радиусы до пересечения с контуром обхода L. При этом, радиусы должны образовать m равных углов в интервале углов от 0 до 2π, тогда интеграл (10) можно заменить суммой конечных приращений Δϕi потенциала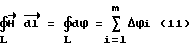
где Δϕi= ϕi+1-ϕi, i = 1, 2, 3, ..., m (12)
Из выражения (11) следует, что для определения циркуляции вектора 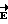 необходимо на контуре обхода выбрать m точек, в которых будет измеряться потенциал ϕi, i = 1, 2, 3, ..., m. По измеренным потенциалам определяем конечные приращения Δϕi по формуле (12) и определяем их сумму по формуле (11).
необходимо на контуре обхода выбрать m точек, в которых будет измеряться потенциал ϕi, i = 1, 2, 3, ..., m. По измеренным потенциалам определяем конечные приращения Δϕi по формуле (12) и определяем их сумму по формуле (11).
Предлагаемое устройство работает следующим образом. При включении ключа l в замкнутой цепи протекает ток от плюсовой клеммы источника тока 2, через амперметр 3, второй неподвижный контакт 4 и второй подвижный 5 контакт подвижной втулки 6, токопроводящий стержень 7, ползунок 8 переменного резистора 9, сам переменный резистор 9, первый подвижный 10 контакт подвижной втулки 6, первый неподвижный 11 контакт, ключ l на минусовую клемму источника тока 2. Амперметр 3 показывает величину тока, которая определяется по выражению (4), т. е. величина тока обратно пропорциональна расстоянию r от высокого стрежня 12, моделирующего бесконечный проводник с током I или от центра шарика 13, насаженного на высокий стержень 12, который моделирует точечный заряд q. Подвижная втулка 6 насажена на высокий стержень 12 и жестко соединена через токопроводящий стержень 7 и переменный резистор 9 с подвижной опорой 14. Ползунок 8 переменного резистора снабжен указателем 15 точки на планшете 16. На планшете изображены контуры обхода с точками, где необходимо проводить измерения напряженности магнитного поля по формуле (5) или потенциала электростатического поля по формуле (6). Вращая линейный переменный потенциометр вокруг высокого стержня 12 или шарика 13, а также, передвигая ползунок 8 указателем 15 находим на контуре обхода планшета 16 нужную точку и осуществляем измерения H или ϕ в этой точке. По алгоритму (8) или (11) находим соответственно циркуляцию вектора 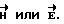
Когда обучаемый определяет циркуляцию вектора 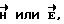 то полагает, что поле создается и есть измеритель соответствующей характеристики поля. В итоге он измеряет величину напряженности H или потенциала ϕ по амперметру в соответствующей точке контура обхода.
то полагает, что поле создается и есть измеритель соответствующей характеристики поля. В итоге он измеряет величину напряженности H или потенциала ϕ по амперметру в соответствующей точке контура обхода.
Предлагаемое устройство по определению циркуляции вектора 
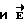 не уменьшает познавательной возможности, т.к. на установке (модели) обучаемый проводит те же операции, которые проводил бы на натуре.
не уменьшает познавательной возможности, т.к. на установке (модели) обучаемый проводит те же операции, которые проводил бы на натуре.
Технико-экономическая эффективность предлагаемого устройства заключается в том, что расширяется диапазон использования устройства, что обеспечивает повышение качества усвоения основных законов физики студентами.
Предлагаемое устройство реализовано на кафедре физики и используется в учебном процессе на лабораторных работах по электромагнетизму.
Литература:
1. Г. А. Рязанов. Опыты и моделирование при изучении электромагнитного поля. Наука, М., 1966.
2. Г.А. Рязанов. Электрическое моделирование с применением вихревых полей. Наука, М., 1969.
3. Ф. В. Кушнир и др. Измерения в технике связи. Связь, М., 1970, с. 385,470.
Стенд для демонстрации свойств магнитного поля. СССР, авт.св. N 1720074, 15.03.92, бюл. 10.
5. Способ демонстрации электрического поля. СССР, авт.св. N 1603424, 30.10.90, бюл. 40.
6. А. С. Гринберг. Генерирование функций с помощью потенциометров. Энергия, М., 1965, с. 149, рис. 8.13.
Устройство содержит переменный резистор (9), ключ (1), первый (11) и второй (4) неподвижный контакт, первый (10) и второй (5) подвижный контакты, планшет (16) с изображением контуров обхода, указатель (15) точки на планшете, закрепленный на ползунке резистора (9), высокий стержень (12), моделирующий бесконечный проводник с током и закрепленный перпендикулярно к планшету, шарик (13), насаженный на высокий стержень, моделирующий электрический точечный заряд, подвижную опору (14), на которой закреплен один конец резистора (9), и токопроводящий стержень (7), на котором перемещается ползунок переменного резистора, подвижную втулку (6), насаженную на высокий стержень и на которой закреплен другой конец резистора (9), на одном конце втулки (6) установлен первый подвижный контакт (10), а на другом - второй подвижный контакт (5), источник тока (2), амперметр (3). Технический результат заключается в расширении функциональных возможностей. 4 ил.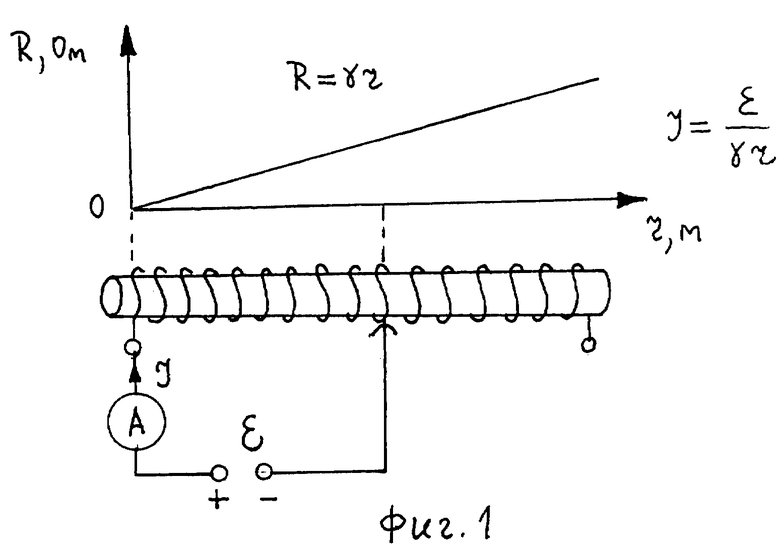
Устройство для определения циркуляции вектора напряженности электрического и магнитного поля, содержащее переменный резистор, отличающееся тем, что в него введены ключ, первый и второй неподвижный контакт, планшет с изображением контуров обхода, указатель точки на планшете, закрепленный на ползунке переменного резистора, высокий стержень, моделирующий бесконечный проводник с током и закрепленный перпендикулярно к планшету, шарик, насаженный на высокий стержень, моделирующий электрический точечный заряд, подвижная опора, на которой закреплен один конец переменного резистора, подвижная втулка, насаженная на высокий стержень и на которой закреплен другой конец переменного резистора, первый подвижный контакт, установленный на одном конце подвижной втулки, второй подвижный контакт, установленный на другом конце подвижной втулки, токопроводящий стержень, на котором перемещается ползунок переменного резистора и закрепленный одним концом с подвижной опорой, а другим концом соединен со вторым подвижным контактом, источник тока, соединенный минусовой клеммой через ключ, первый неподвижный контакт и первый подвижный контакт с неподвижным контактом переменного резистора, амперметр, соединенный одной клеммой с плюсовой клеммой источника тока, а второй клеммой через второй неподвижный контакт и второй подвижный контакт с токопроводящим стержнем.
| Учебный прибор по электротехнике | 1987 |
|
SU1490685A1 |
| СПОСОБ ДЕМОНСТРАЦИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ | 1992 |
|
RU2079895C1 |
| УСТРОЙСТВО для ОПРЕДЕЛЕНИЯ СИЛОВЫХ ЛИНИЙ МАГНИТНОГО ПОЛЯ | 0 |
|
SU313182A1 |
| Кушнир Ф.В | |||
| Электрорадиоизмерения | |||
| - Л.: Энергия, 1975, c.54-61 | |||
| DE, 2507837 В2, 02.07.81, Гринберг А.С | |||
| Генерирование функций с помощью потенциометров | |||
| - М.: Энергия, 1965, с | |||
| Подъемник для выгрузки и нагрузки барж сплавными бревнами, дровами и т.п. | 1919 |
|
SU149A1 |
Авторы
Даты
1999-09-10—Публикация
1998-05-26—Подача