Изобретение относится к измерительной технике и автоматике и может быть использовано в пеленгаторах, при обработке сигналов с датчиков звуковых, электромагнитных колебаний или потоков частиц.
Известны устройства для обработки сигналов, реализующие корреляционный способ (например, а.с. СССР N 1352501, G 06 F 15/336, опубл. 15.11.87), заключающийся в получении спектров двух сигналов и их обработки с целью вычисления значений корреляционной функции. Этот способ обработки оптимален только в классе линейных обработок сигналов.
Наиболее близким к предлагаемому является способ обнаружения сигналов от источника излучений путем корреляционной обработки (а. с. СССР N 1472916 G 06 F 15/336, опубл. 15.04.89), включающий получение сигналов с двух датчиков, преобразование их в спектральные представления, перемножение комплексных амплитуд гармоник двух спектров и получение комплексного взаимного спектра, который подвергают обратному преобразованию Фурье для вычисления значений корреляционной функции.
Недостатком этого способа обработки является то, что он оптимален только в классе линейных обработок сигналов (в некоторых случаях глобальный максимум имеет большую ширину и велика амплитуда боковых лепестков) и поэтому нуждается в улучшении показателей по помехоустойчивости (надежное определение факта наличия источника) и повышении точности определения положения глобального максимума (для точной оценки координат источника излучения).
Таким образом, задачей изобретения является создание такого способа обработки, результат Z которого имеет узкий глобальный максимум с малыми боковыми лепестками и, как следствие этого, снижение ошибок при обнаружении сигналов, смешанных с шумами, и повышение точности оценок местонахождения источника сигналов.
Поставленная цель достигается тем, что при обработке данных для обнаружения источника излучения выполняется преобразование первого сигнала в спектральное представление Фурье и преобразование второго сигнала в комплексно-сопряженное спектральное представление Фурье, получение взаимного спектра путем перемножения комплексных амплитуд гармоник полученных спектров первого и второго сигналов и последующее обратное преобразование Фурье, при этом предлагается перед обратным преобразованием Фурье произвести расширение взаимного спектра путем выравнивания модулей амплитуд его гармоник на константу, оставляющую неизменной сумму квадратов амплитуд модулей всех гармоник.
Сущность способа заключается в том, что учитываются свойства комплексного взаимного спектра. Известны свойства спектрального преобразования S для функции
f(x)•S(ω) = ∫
Если функции f1(x) и f2(x) отличаются только сдвигом на величину d по переменной x: f2(x) = f1(x-d), то их комплексные спектры отличаются только фазовым множителем e-jωd:S1(ω) = ∫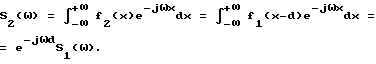
Из этих соотношений видно, что модули спектральных амплитуд взаимного спектра зависят от характеристик конкретного объекта, а фазовый спектр несет в себе информацию о расстоянии. Информацию о величине сдвига d получают путем нахождения разности фаз для каждой гармоники спектров S1, S2. Разности фаз для всех гармоник можно получить в виде фазовой составляющей спектра Sв(ω), который получается умножением S1 на комплексное сопряжение спектра S2:
Sв(ω) = S1(ω)×S
где * является знаком комплексного сопряжения. Sв(ω) называется взаимным спектром сигналов f1(x) и f2(x). Комплексно-сопряженный спектр S
Обратное Фурье-преобразование Sв(ω) является кросскорреляционной функцией сигналов f1(x) и f2(x), которая широко используется в технических приложениях для определения величины сдвига d. Ошибка определения сдвига во многом зависит от ширины глобального максимума и от наличия и амплитуды боковых лепестков, которые всегда присутствуют около этого максимума. Ширина максимума зависит от ширины взаимного спектра, самый узкий максимум получится при равномерном спектре.
Описываемый способ предполагает получение нового спектра S(ω) путем расширения взаимного спектра (для получения узкого глобального пика после обратного преобразования) с сохранением фазового спектра, определяющего величину сдвига d. Амплитудный спектр необходимо выровнять на константу таким образом, чтобы энергия спектра S(ω) осталась равной энергии спектра Sв(ω):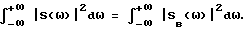
При технических реализациях это условие выполнится, если S(ω) будет равномерным спектром, и сумма квадратов модулей его гармоник будет равна сумме квадратов гармоник спектра Sв(ω).
Способ может быть реализован устройством, блок-схема которого показана на фиг. 1. Схема включает блок 1 памяти для хранения выборки одномерного сигнала f1, блок 2 памяти для хранения выборки одномерного сигнала f2, блок 3 выполнения прямого Фурье-преобразования, блок 4 выполнения обратного Фурье-преобразования, блоки 5 и 6 являющимися памятью для хранения результатов работы блоков 3 и 4 соответственно (спектры S1(ω) и S
Если входные реализации сигналов представляют собой выборки из двухмерной совокупности (например, изображения на плоскости, сдвинутые относительно друг друга), то блоки 3, 4, 10 осуществляют двухмерные Фурье-преобразования, а результат Z, хранящийся в блоке 11, есть функция двух сдвиговых аргументов. Пику функции Z соответствуют два аргумента - сдвиги по "горизонтальной" и "вертикальной" координатам.
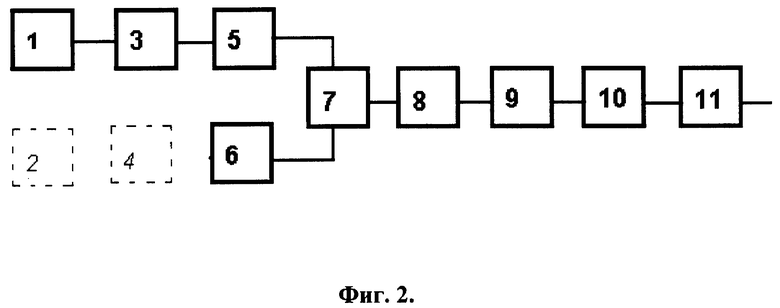
На Фиг. 2 показана схема, реализующая способ для случая, когда один из сигналов заранее известен. Например, при активной локации излучаемый сигнал известен, поэтому на блок 1 поступает выборка сигнала отраженного целью, а в блоках 2, 4 отпадает необходимость, так как данные о сопряженном спектре излучаемого сигнала могут быть заранее сохранены в памяти блока 6.
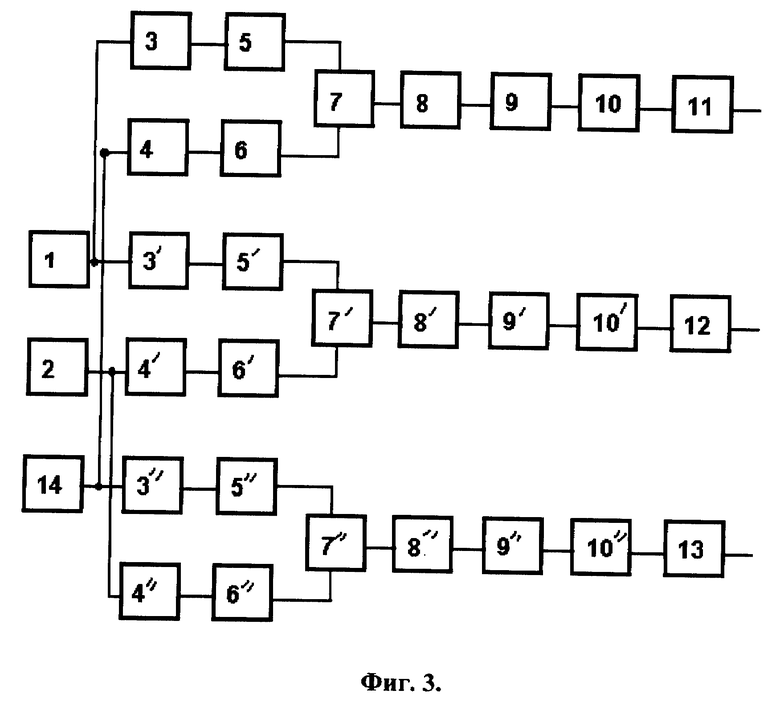
Пример реализации способа для обнаружения сейсмических источников звуковых колебаний показан на Фиг. 3. Предполагается, что пеленгация производится тремя датчиками, не расположенными на одной прямой. Выборки данных из датчиков помещаются в память блоков 1, 2, 14, блоки 3, 3', 3'' выполняют прямое преобразование Фурье, 4, 4', 4'' выполняют обратное преобразование, 5, 5', 5'' хранят прямые спектры, 6, 6', 6'' хранят комплексно-сопряженные спектры, 7, 7', 7'' вычисляют взаимные спектры, 8, 8', 8'' хранят взаимные спектры, 9, 9', 9'' расширяют взаимные спектры, 10, 10', 10'' производят обратное преобразование Фурье, блоки 11, 12, 13 хранят результаты обработки для всевозможных пар датчиков. По полученным результатам определяются взаимные задержки сигналов для каждой пары датчиков, и местоположение источника на плоскости определяется в точке пересечения гиперболических линий, соответствующих полученным задержкам.
Реализация способа поясняется следующими примерами.
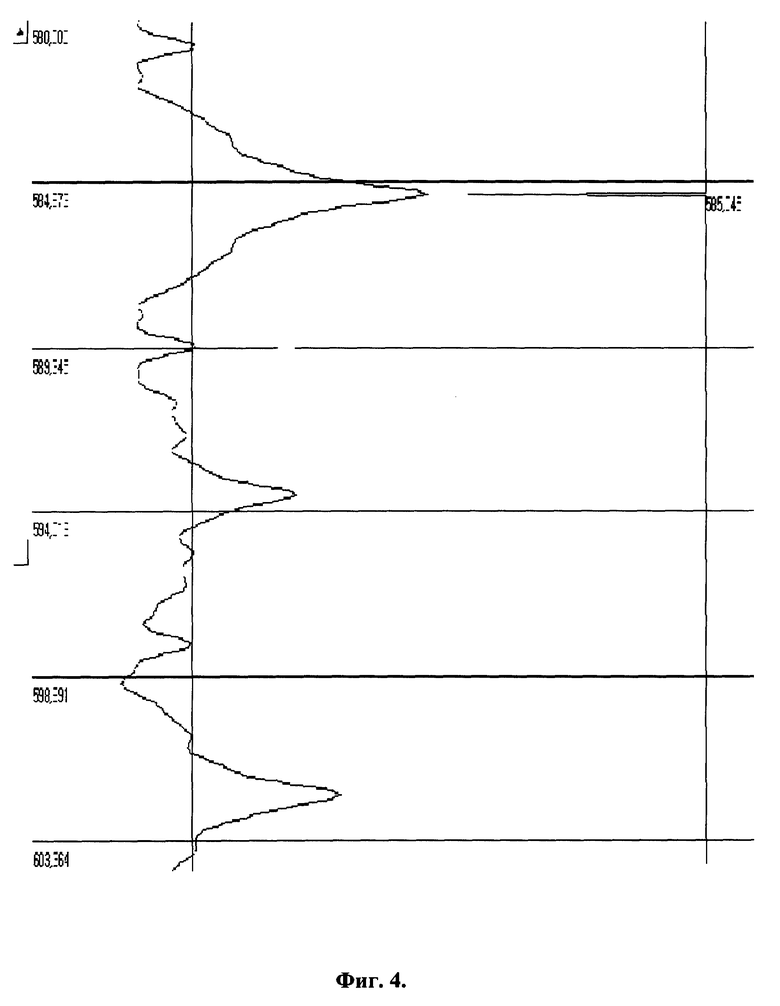
Пример 1 (Фиг.1). Обнаружение и оценка координат источника звука в трубопроводе. Z есть функция времени относительной задержки сигнала от источника до датчиков (микрофонов). Временная задержка индицируется по положению глобального максимума результата обработки Z с точностью, зависящей от ширины максимума. Зная время задержки сигнала и скорость распространения сигнала в среде трубопровода, определяют координаты источника. На Фиг. 4 одновременно показаны кросскорреляционная функция (слева) и функция Z, полученная по предлагаемому способу (справа) для случая, когда звуковой сигнал распространялся в линейной среде со скоростью 5000 м/сек. Результат Z четко указывает на то, что источник звука находится на отметке 585.4 м. Функция кросскорреляции имеет гораздо более широкий центральный пик, что обуславливает худшую точность локации местоположения источника колебаний.
Пример 2 (Фиг. 1). Определение координатного дрейфа над динамическим, случайно-неоднородным рельефом по наблюдениям изменения картины рельефа. Пусть некоторый летающий аппарат "висит" над облачным покровом, и измерительная аппаратура находится на борту аппарата. Стоит задача отслеживать координатный дрейф аппарата на основании визуальных наблюдений подстилающей облачности. Данными являются последовательная пара кадров визуальных изображений облачности. В этом случае выборки f1 и f2 являются яркостными функциями, зависящими от двух пространственных координат. Разумеется преобразования Фурье в блоках обработки в этих случаях двухмерные. Выход обработчика является функцией координатного сдвига. Координатный сдвиг индицируется по положению максимума результата обработки с точностью, зависящей от ширины глобального максимума.
Пример 3 (Фиг.2). Активная локация. Выборка f1 - это отраженный от цели сигнал, принятый антенной. Выборка f2 - это опорный сигнал (т.е. сигнал, излученный в сторону цели). Выходной результат блока обработки в момент максимума (превышающий некоторый порог) указывает на факт наличия цели. Ширина центрального пика максимума определяет точность измерения момента прихода на антенну отраженного сигнала и, следовательно, дальность до цели. Если форма сигнала известна заранее (сигнал не шумоподобный), то можно сразу в блок обработки ввести комплексно сопряженный спектр опорного сигнала; в этом случае отпадет нужда в осуществлении Фурье-преобразования для реализации сигнала f2. Подобным образом обработку осуществляет линейное устройство, известное под названием "согласованный фильтр". Устройство, применяющее предлагаемый метод обработки, является "нелинейным согласованным фильтром".
Пример 4 (Фиг. 3). Пассивная локация сейсмического источника. Пусть где-то имеется сейсмический постоянно действующий источник на фоне посторонних сравнительно кратковременных шумов. При достаточно большом времени наблюдения можно определить координаты постоянного источника на земной поверхности (т. е. всего 2 координаты). Для таких измерений устанавливают не менее трех датчиков, не лежащих на одной линии. Если есть уверенность, что источник лежит строго вне или строго внутри треугольника, по вершинам которого стоят датчики, то для оценки поверхностных координат нужно 3 датчика. Для оценки пространственных координат необходимо 4 некомпланарных датчика. В данном примере количество полученных реализаций разумеется равно количеству датчиков. При помощи предлагаемой обработки измеряют относительные задержки для всех пар датчиков. На основании известных времен задержек вычисляют координаты источника.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТНОГО СДВИГА МЕЖДУ РАДИОСИГНАЛАМИ | 2017 |
|
RU2668342C2 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ ШУМОВЫХ ГИДРОАКУСТИЧЕСКИХ СИГНАЛОВ В ВИДЕ ЗВУКОРЯДА НА ОСНОВЕ ВЫЧИСЛЕНИЯ ИНТЕГРАЛЬНОГО ВЕЙВЛЕТ-СПЕКТРА | 2011 |
|
RU2464588C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ УЗКОПОЛОСНЫХ ШУМОВЫХ ГИДРОАКУСТИЧЕСКИХ СИГНАЛОВ НА ОСНОВЕ ВЫЧИСЛЕНИЯ ИНТЕГРАЛЬНОГО ВЕЙВЛЕТ-СПЕКТРА | 2007 |
|
RU2367970C2 |
| СПОСОБ ПОЛУЧЕНИЯ СЕЙСМИЧЕСКОГО РАЗРЕЗА | 1991 |
|
RU2022310C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ ИСТОЧНИКА РАДИОИЗЛУЧЕНИЯ | 2015 |
|
RU2642846C2 |
| СПОСОБ ИЗМЕРЕНИЯ ВНЕШНЕБАЛЛИСТИЧЕСКИХ ХАРАКТЕРИСТИК СНАРЯДА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2515580C1 |
| СПОСОБ ИСПЫТАНИЙ ЛАЗЕРНОЙ БАЛЛИСТИЧЕСКОЙ ИЗМЕРИТЕЛЬНОЙ СИСТЕМЫ | 2020 |
|
RU2765137C2 |
| СПОСОБ ОБНАРУЖЕНИЯ ИМПУЛЬСНЫХ СИГНАЛОВ С НЕИЗВЕСТНЫМИ ПАРАМЕТРАМИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2006 |
|
RU2321018C1 |
| СПОСОБ И УСТРОЙСТВО БЫСТРОГО ВЫЧИСЛЕНИЯ ФУНКЦИИ НЕОПРЕДЕЛЕННОСТИ СИГНАЛА С УЧЕТОМ РЕВЕРБЕРАЦИОННОЙ ПОМЕХИ | 2009 |
|
RU2487367C2 |
| УСТРОЙСТВО ГИДРОМЕТЕОРОЛОГОАКУСТИЧЕСКИХ НАБЛЮДЕНИЙ ЗА АКВАТОРИЕЙ МОРСКОГО ПОЛИГОНА | 2005 |
|
RU2300781C1 |
Изобретение относится к измерительной технике и автоматике. Способ заключается в том, что для получения более узкого глобального максимума при обнаружении источника излучения выполняют преобразование первого сигнала в спектральное преобразование Фурье и преобразование второго сигнала в комплексно-сопряженное спектральное представление Фурье, получение взаимного спектра, получение расширенного спектра из взаимного спектра путем выравнивания модулей амплитуд его гармоник на константу, оставляющую неизменной сумму квадратов амплитуд модулей всех гармоник, и последующее обратное преобразование Фурье расширенного спектра. Достигаемым техническим результатом является получение глобального максимума на порядок уже, чем у кроскорреляционной функции, а следовательно, и уменьшение уровня боковых лепестков. 4 ил.
Способ обработки данных для обнаружения источника излучения, включающий преобразование первого сигнала в спектр Фурье и преобразование второго сигнала в комплексно-сопряженный спектр Фурье, получение взаимного спектра путем перемножения комплексных амплитуд гармоник полученных спектров первого и второго сигналов и последующее обратное преобразование Фурье взаимного спектра, отличающийся тем, что перед обратным преобразованием Фурье взаимный спектр подвергают расширению путем выравнивания модулей амплитуд его гармоник на константу, оставляющую неизменной сумму квадратов амплитуд модулей всех гармоник.
| Устройство для вычисления корреляционной функции | 1987 |
|
SU1472916A2 |
| Цифровой обнаружитель-измеритель частоты | 1989 |
|
SU1797127A1 |
| ЦИФРОВОЙ ФИЛЬТР | 1997 |
|
RU2123758C1 |
| DE 3136625 C1, 31.03.83 | |||
| US 4882668 A, 21.11.89 | |||
| Знакоформирующее устройство | 1977 |
|
SU805401A1 |
Авторы
Даты
2000-01-10—Публикация
1999-05-11—Подача