СПОСОБ И УСТРОЙСТВО БЫСТРОГО ВЫЧИСЛЕНИЯ ФУНКЦИИ НЕОПРЕДЕЛЕННОСТИ СИГНАЛА С УЧЕТОМ РЕВЕРБЕРАЦИОННОЙ ПОМЕХИ Российский патент 2013 года по МПК G01S15/00 G01S13/00 

Предлагаемое изобретение относится к области гидролокации и радиолокации, а именно к способам согласованной фильтрации сигналов на фоне реверберационной помехи и реализующим их устройствам, а также может быть использовано в радио- и гидролокационных системах при определении координат и параметров движения цели (КПДЦ).

Как правило, в гидролокационных системах при корреляционной обработке учитываются дальность [1, 2, 3, 4, 5], радиальная скорость цели. На практике разрешающая способность локационной системы анализируется на основе функции неопределенности (ФН) Вудворда. В основе такого анализа лежит допущение о постоянстве скорости цели в пределах длительности сигнала и пренебрежимо малых искажениях модулирующей функции. Так в работе [6] приведена допустимая доплеровская расстройка в гидролокаторе. Приближенно полагают, что можно использовать аппроксимацию эффекта Доплера простым сдвигом спектра при выполнении условия 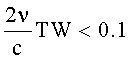$$\frac{2\nu }{c}TW<0.1$$ , где ν - скорость объекта, с - скорость распространения сигнала, Т - длительность излучаемого сигнала, W - ширина полосы частот излучаемого сигнала.

Известно, что реализация оптимального приема при решении задачи обнаружения сигналов на фоне реверберационных помех во многом определяется уровнем знаний априорной информации о принимаемом сигнале [7].

Поэтому принятый эхо-сигнал y(t) выражается в виде свертки излученного импульса s(t) с импульсной характеристикой среды и цели h(t). Таким образом,

$$y\left(t\right)=s\left(t\right)*h\left(t\right).\left(1\right)$$

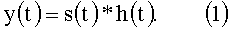
Поскольку число рассеивателей и их сила для любого момента времени при формировании реверберации являются функциями расстояния, то и среднее значение, и дисперсия, связанные с огибающей, также будут функциями расстояния, т.е. зависят от времени.

Спектральная плотность реверберационной помехи является нестационарной функцией времени и частоты N(f, t) и с точностью до переменной во времени мощности может быть приближенно записана

$$N\left(f,t\right)=P\left(t\right){\left|S\left(f\right)\right|}^2,\left(2\right)$$

где S(f) - спектральная плотность сигнала,

P(t) - мощность реверберации.

Так как спектральная плотность - это математическое ожидание значения квадрата амплитуды s_R(t) в частотной области, то

$$N\left(t\right)={\left|S\left(f\right)\right|}^{2}K{\sigma }_{an}^2,$$

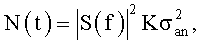
где K - число рассеивающих элементов.

Из выражения (2) следует, что спектральная плотность реверберации, принятая из ограниченного интервала, имеет тот же вид, что и спектр мощности излученного сигнала. Изменение амплитуды реверберации зависит от изменения расстояния до объекта. Вследствие эффекта Доплера частота принятого сигнала от элемента рассеяния сдвинута на величину, пропорциональную радиальной скорости цели относительно радио- или гидроакустической станции. Учитывая сигналы, принятые из кольцевой зоны с центром, совпадающие с местом движущейся радиолокационной или гидроакустической станции, получаем при этом, что доплеровское смещение лежит в пределах от 2V/λ₀ до -2V/λ₀, где V - относительная скорость цели, λ₀ - длина волны несущей частоты сигнала.

Отсюда следует, что для зондирующего сигнала с шириной полосы частот, малой по сравнению с несущей, спектр принятого сигнала от одиночного рассеивателя приблизительно повторяет спектр зондирующего сигнала, сдвинутого по частоте на величину доплеровского смещения f_d=2V/λ₀, где V - относительная радиальная составляющая скорости, λ₀ - длина волн, соответствующая несущей частоте излученного сигнала.

Таким образом, спектр принятого сигнала является суммой спектров от отдельных рассеивателей с весом, определенным квадратом взаимной характеристики направленности [7]. Доплеровское смещение в пределах ширины характеристики направленности приводит к уширению спектра принятого сигнала.

В диапазоне от f₀+2V/λ₀ до f₀-2V/λ₀ мощность реверберационной помехи уменьшается на величину, определяемую уровнем бокового поля характеристики направленности. Поскольку величина доплеровского смещения не может превосходить 2V/λ, спектр на частотах выше f₀+2V/λ₀ определяется, прежде всего, формой спектра зондирующего импульса с центром на частоте f₀+2V/λ.

Близкой по технической сущности к предлагаемому изобретению является система CAVORT [8] (система обработки эхо-сигналов от целей [9, 10, 11, 12]). Эта система работает следующим образом: принятые импульсы пропускают через линию задержки (ЛЗ) на промежуточной частоте с общим числом отводов N. Эти отводы соединены с двумя рядами смесителей. Верхний ряд смесителей производит частотные сдвиги fν, 2fν, …, (N-1)fν. Получающиеся сдвиги в любой момент времени характеризуют относительную скорость цели. Подстройка этого согласования под цели, испытывающие ускорение движения, достигается дальнейшим сдвигом, обеспечиваемым вторым рядом смесителей.

Недостатком способа является сложность его технической реализации, т.к. требуемое число фильтров при этом очень велико и составляет несколько сотен. С учетом пространственной обработки это требует очень больших вычислительных затрат.

Наиболее близким к предлагаемому изобретению является способ согласованной фильтрации принятого сигнала [13].

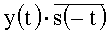
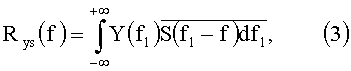
Рассмотренный способ позволяет выделить сигнал при наличии помехи в условиях доплеровского эффекта. Суть способа состоит в следующем. В среду излучают зондирующий импульс. Входная реализация и эталон перемножаются между собой $$y\left(t\right)\cdot \overline{s\left(-t\right)}$$ , где ^- - представляет собой символ комплексного сопряжения. К результату перемножения применяется преобразование Фурье, в результате которого получают спектральную взаимно корреляционную функцию (ВКФ) вида:

$$R_{ys}\left(f\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}Y\left(f_1\right)\overline{S\left(f_1-f\right)d{f}_1},\left(3\right)}$$

где f - частотный сдвиг эхо-сигнала вследствие эффекта Доплера.

Результирующий отклик корреляционной функции сравнивается с пороговым напряжением. Обработка производится в реальном масштабе времени, т.е. отсчеты входной реализации обновляются в соответствии с теоремой Котельникова. Превышение порогового значения происходит в момент компенсации задержки τ=0. При этом принимается решение об обнаружении цели, а сам момент будет соответствовать дистанции до цели. Рассмотренный способ является оптимальным с точки зрения отношения сигнал/помеха для детерминированного сигнала в условиях «белого» шума. В технических решениях вместо (3) рассматривают функционал:

$$R_{ys}\left(t,f\right)={\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}Y\left(f_1\right)\overline{S\left(f_1-f\right)}}\exp \left(i2\pi f_{1}t\right)d{f}_1\left(4\right)$$

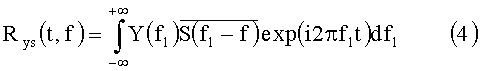
Ввиду большой практической важности выражение (4) определяют как взаимную функцию неопределенности, для вычисления которой находят результат обратного преобразования Фурье от перемножения спектра входной реализации и сдвинутых спектров эталонного сигнала.

Данное правило (4) решает задачу согласованной фильтрации при наличии сдвига и доплеровского эффекта в условиях «белого шума». Однако в гидролокационных системах кроме воздействия шума среды необходимо учитывать влияние реверберационной помехи. Не учет данного влияния проявляется в снижении помехоустойчивости системы фильтрации.

Выражение (4) предполагает вычисление свертки прямым методом, основанным на произведении многочленов и содержащим большое количество операций, равное произведению степеней этих многочленов.

Целью предлагаемого изобретения является:

1) повышение быстродействия вычисления взаимной функции неопределенности;

2) повышение помехоустойчивости системы фильтрации за счет учета влияния реверберационной помехи.

Поставленная цель достигается применением быстрых алгоритмов и формированием для вычисления взаимной функции неопределенности эталонного сигнала с учетом априорных данных о спектральной плотности реверберационной помехи.

1. Способ быстрого вычисления функции неопределенности сигналов с учетом реверберационной помехи

Суть способа состоит в следующем. Оптимальным обнаружителем детерминированного сигнала на фоне аддитивной помехи является согласованный фильтр, имеющий частотную характеристику вида [7]:

$$H\left(f,t\right)=\frac{\overline{S\left(f\right)}}{N\left(f,t\right)}$$ ,

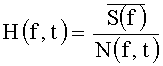
где S(f) - комплекснозначная спектральная плотность сигнала,

N(f, t) - энергетическая спектральная характеристика помехи.

Однако при наличии доплеровского эффекта реверберационной отклик согласованного фильтра [14, 12] определяется в виде:

$$\Theta \left(t,f\right)={\left|{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}Y\left(f_1\right)\frac{\overline{S\left(f_1-f\right)}}{N\left(f_1,t\right)}\exp \left(i2\pi f_{1}t\right)d{f}_1}\right|}^2.\left(5\right)$$

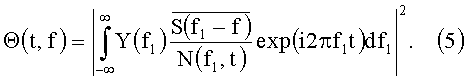
При условии Y(f)=S(f) для значений t=0 и f=0 значение взаимной функции неопределенности достигает максимума, который равен:

$$K\left(\mathrm{0,0}\right)={\left|{\displaystyle \int \frac{{\left|S\left(f_1\right)\right|}^2}{N\left(f_1\mathrm{,0}\right)}d{f}_1}\right|}^2.\left(6\right)$$

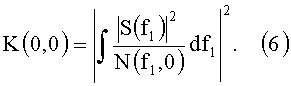
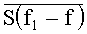
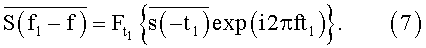
В операторе (5) спектр эталонного сигнала $$\overline{S\left(f_1-f\right)}$$ можно представить:

$$\overline{S\left(f_1-f\right)}=F_{t_1}\left\{\overline{s\left(-t_1\right)}\exp \left(i2\pi f{t}_1\right)\right\}.\left(7\right)$$

Подставляя выражение (7) в выражение (5), получим:

$$\Theta \left(t,f\right)={\left|{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}Y\left(f_1\right)\frac{F_{t_1}\left\{\overline{s\left(-t_1\right)}\exp \left(i2\pi f{t}_1\right)\right\}}{N\left(f_1,t\right)}}\exp \left(i2\pi f_{1}t\right)d{f}_1\right|}^2\left(8\right)$$

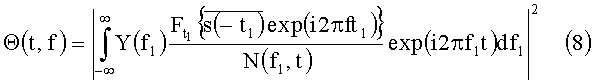
Запишем (8) с помощью обратного преобразования Фурье по f₁:

$$\Theta \left(t,f\right)={\left|F_{f_1}^{-1}{F}_{t_1}\left(\overline{s\left(-t_1\right)}\frac{Y\left(f_1\right)}{N\left(f_1,t\right)}\exp \left(i2\pi f{t}_1\right)\right)\right|}^2.\left(9\right)$$

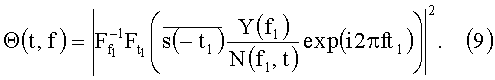
Выражение (9) позволяет сформировать способ быстрого вычисления взаимной функции неопределенности с учетом реверберационной помехи и является основой для предлагаемого способа обнаружения сигналов при наличии реверберационной помехи.

Из анализа соотношения (9) можно сделать вывод, что для формирования отклика взаимной функции неопределенности необходимо получить результат перемножения инвертированного и сопряженного эталонного сигнала, спектральной характеристики входной реализации, массива двухмерных экспонент, деление результата перемножения на сформированную энергетическую спектральную характеристику реверберации:

$$R\left(t_1,t,f_1,f\right)=\overline{s\left(-t_1\right)}Y\left(f_1\right)\exp \left(i2\pi f{t}_1\right)/N\left(f_1,t\right)$$

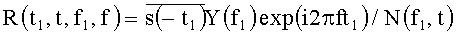
и применение к результату деления R(t₁, t, f₁, f) обратного и прямого преобразований Фурье по переменным f₁, t₁.

Таким образом, применение для вычисления функции неопределенности сигналов с учетом реверберационной помехи только операций умножения и быстрых алгоритмов вычисления преобразований Фурье позволяет производить вычисления более эффективно, чем вычисления взаимной функции неопределенности в соответствии с алгоритмом, записанным формулой (4).

Способ вычисления функции неопределенности сигналов с учетом реверберационной помехи включает в себя следующие операции:

1. Вычисление спектра Фурье Y(f₁) принятой реализации y(t₁) и обнуление отрицательных частот (преобразование его в спектр аналитического сигнала): Y_A(f₁)=Y(f), при f>0 и Y_A(f₁)=0 при f≤0.

2. Формирование (или извлечение из памяти заранее рассчитанного) двухмерного массива экспонент E(f, t₁)=ехр(i2πft₁).

3. Формирование (или извлечение из памяти заранее смоделированной) спектральной плотности реверберации N(f₁, t).

4. Комплексное сопряжение и отражение от нуля 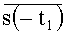$$\overline{s\left(-t_1\right)}$$ эталонного сигнала s(t₁).

5. Перемножение сопряженного эталонного сигнала 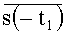$$\overline{s\left(-t_1\right)}$$ , экспонент Е(f, t₁) и сформированной энергетической спектральной характеристикой реверберации N(f₁, t).

6. Обратное двухмерное преобразование Фурье по t₁ и f₁:

$$R\left(t,f\right)=F_{f_1}^{-1}{F}_{t_1}\left(\overline{s\left(-t_1\right)}\frac{Y\left(f_1\right)}{N\left(f_1,t\right)}\exp \left(i2\pi f{t}_1\right)\right)$$ .

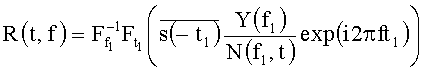
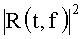
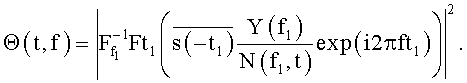
7. Квадратичное детектирование результата обратного двухмерного преобразования Фурье (вычисление квадрата модуля $${\left|R\left(t,f\right)\right|}^2$$ ):

$$\Theta \left(t,f\right)={\left|F_{f_1}^{-1}F{t}_1\left(\overline{s\left(-t_1\right)}\frac{Y\left(f_1\right)}{N\left(f_1,t\right)}\exp \left(i2\pi f{t}_1\right)\right)\right|}^2.$$

Операции 2-5 не требуют наличия входной реализации, и, следовательно, могут быть проведены заранее, а результаты расчетов храниться в постоянных запоминающих устройствах (ПЗУ).

Применение дополнительных по сравнению с прототипом операций для обнаружения сигналов при наличии доплеровского эффекта и реверберационной помехи позволило получить положительные эффекты, заключающиеся в повышении помехоустойчивости обнаружения сигналов, увеличении эффективности вычисления двухмерного отклика согласованного фильтра.

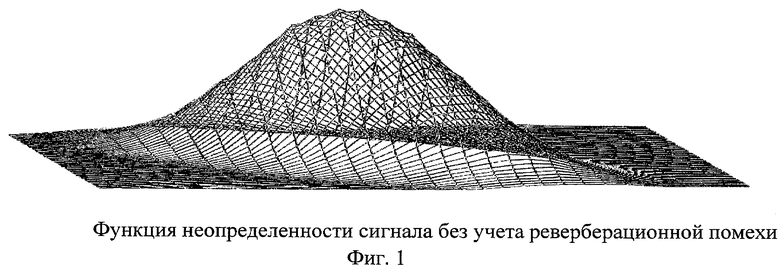
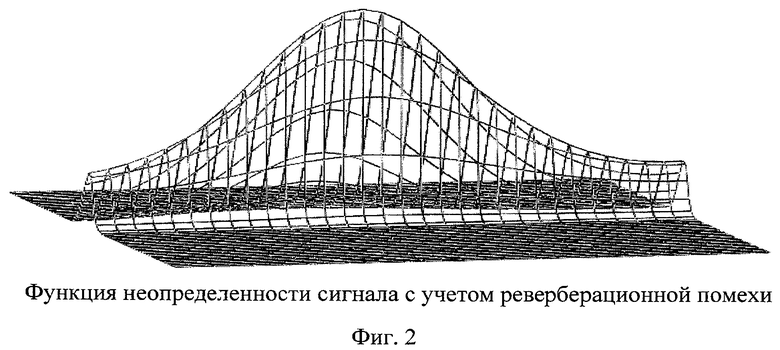
Для проверки работы предлагаемого способа было проведено моделирование в системе MathCad. Результат моделирования без учета влияния реверберационной помехи представлен на фиг.1, а с учетом влияния реверберационной помехи на фиг.2.

Предложенный способ согласованной фильтрации в условиях влияния реверберационной помехи позволяет получить выигрыш в помехоустойчивости до 6 Дб.

2. Устройство быстрого вычисления функции неопределенности сигналов с учетом реверберационной помехи

Устройство, реализующее предлагаемый способ обнаружения сигналов на фоне реверберационной помехи, приведено на фиг.3. Устройство содержит в себе следующие блоки:

1) блок 1 - аналого-цифровой преобразователь (АЦП);

2) блок 2 - рециркулятор;

3) блок 3 - вычислитель БПФ,

4) блок 4 - формирователь аналитического сигнала (устройство обнуления отрицательных частот),

5) блок 5 - ПЗУ,

6) блок 6 - комплексный перемножитель,

7) блок 7 - вычислитель обратного двухмерного БПФ,

8) блок 8 - вычислитель квадрата модуля,

9) блок 9 - управляющее устройство.

Блок аналого-цифровой преобразователя 1 предназначен для представления принятой реализации в цифровой форме.

Блок рециркулятора 2 предназначен для хранения выходных отсчетов АЦП (блок 1).

Блок быстрого преобразования Фурье (БПФ) 3 предназначен для нахождения спектра сигнала и широко распространен в цифровой обработке сигналов [15].

Блок формирования аналитического сигнала 4 предназначен для обнуления отсчетов БПФ, номера которых больше половины длины выборки.

Блок постоянного запоминающего устройства (ПЗУ) 5 предназначен для хранения массива значений результата перемножений комплексно-сопряженного эталонного процесса, массива экспонент и оценки спектральной плотности реверберационной помехи.

Блок комплексного перемножения 6 предназначен для перемножения отсчетов спектра принятой реализации со значениями хранящихся в ПЗУ.

Блок обратного быстрого двухмерного преобразования Фурье (БПФ) 7 предназначен для нахождения отсчетов сигнала во временной области и широко распространен в цифровой обработке сигналов [16].

Блок вычислителя квадрата модуля 8 предназначен для возведения в степень 2 значений отсчетов с выхода блока 7.

Блок управляющего устройства 9 предназначен для синхронной работы всех блоков.

Принцип действия устройства заключается в следующем. Реализация входного процесса x(t) поступает на вход АЦП (блок 1) с частотой

дискретизации, удовлетворяющей требованиям теоремы Котельникова:

$$f_{\partial }=\frac{1}{\Delta t_{\partial }}\ge 2f_{в}$$ .

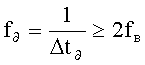
С выхода АЦП (блок 1) дискретные отсчеты поступают на вход рециркулятора (блок 2), где формируется и с каждым новым отсчетом обновляется текущая дискретная выборка s(n) длиной N-отсчетов. Длина выборки N определяется длительностью излучаемого сигнала и интервалом дискретизации: 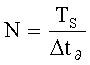$$N=\frac{T_S}{\Delta t_{\partial }}$$ . Сформированная, текущая дискретная выборка входного процесса s(n) поступает на вход вычислителя БПФ (блок 3), с выхода которого комплексный спектр S(n) поступает на вход блока формирования аналитического сигнала (блок 4), с выхода которого поступает на вход комплексного перемножителя (блок 6), на другой вход которого поступает вычисленный заранее аналитический эталонный сигнал, хранящийся в ПЗУ (блок 5). Результат перемножения поступает на вход вычислителя обратного двухмерного БПФ (блок 7). С выхода вычислителя обратного двухмерного БПФ (блок 7) результат поступает на вход вычислителя квадрата модуля (блок 8), выход которого является выходом устройства.

Устройство управления (блок 9) осуществляет синхронизацию работы аналого-цифрового преобразователя (блок 1), рециркулятора (блок 2), блока вычислителя быстрого преобразования Фурье (блок 3), блока формирования аналитического сигнала (блок 4), ПЗУ (блок 5), комплексного перемножителя (блок 6), вычислителя обратного двухмерного БПФ (блок 7), вычислителя квадрата модуля (блок 8).

Для реализации данного способа быстрого вычисления функции неопределенности сигналов с учетом реверберационной помехи требуется одна операция прямого БПФ и одна операция двухмерного обратного БПФ (соответственно 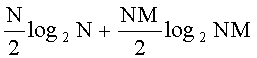$$\frac{N}{2}{\log }_{2}N+\frac{NM}{2}{\log }_{2}NM$$ операций умножения [15]).

Литература

1. Келли. Радиолокационное измерение дальности, скорости и ускорения, Зарубежная радиоэлектроника (ЗР), N2, 1962. - С.35.

2. Патент N 4282589 США, 1981, Корреляционный способ измерения дальности.

3. Патент N 3938147 США, 1976, ЧМ доплеровская система измерения дальности.

4. Заявка N 1482816 Великобритания, Способ и устройство для измерения доплеровского частотного сдвига.

5. Заявка N 56-41953 Япония, 1981, Способ и прибор для измерения расстояния с помощью РЛС непрерывного излучения с ЧМ.

6. Крамер. Допустимая расстройка скорости и ускорения в высокочувствительных широкополосных корреляционных гидролокаторах с линейной ЧМ, ТИИЭР, т.55, N 5, 1967. - С.3.

7. Бурдик B.C. Анализ гидроакустических систем. Л., Судостроение, 1988 г. - С.329-333.

8. Киблер. КЭВОРТ - устройство оптимальной обработки пачечного радиолокационного сигнала с учетом ускорения целей, ЗР N, 1968. - С.27-33.

9. АС № 537315 (СССР) от 30.11.76. Способ определения скорости движения судна относительно дна.

10. Заявка N 2605933 ФРГ, Способ измерения расстояния и скорости, основанный на использовании импульсной доплеровской РЛС.

11. Крамер. Допустимая расстройка скорости и ускорения в высокочувствительных широкополосных корреляционных гидролокаторах с линейной ЧМ. ТИИЭР, т.55, N 5, 1967. - С.3.

12. Шмарев Е.И. и др. Оптическое вычисление функции неопределенности сигналов (обзор). ЗР N 10, 1981. - С.41-43.

13. Бурдик B.C. Анализ гидроакустических систем. - Л.: Судостроение, 1988 г. - Стр.191-194.

14. Келли, Вишнер. Теория согласованной фильтрации целей, движущихся ускоренно с высокими скоростями. ЗР N 10, 1965. - С.38.

15. Применение цифровой обработки сигналов. / Под ред. Оппенгейма Э., - М: Мир, 1980. - С.284, 417-418.

16. Мирский Г. Электронные измерения. - М.: Радио и связь, 1986. - С.126-140. А.С. N 832490 (СССР) от 28.05.81. Анализатор спектра.

Использование: гидролокация и радиолокация. Сущность: устройство для вычисления функции неопределенности сигнала с учетом реверберационной помехи содержит аналого-цифровой преобразователь, выход которого соединен с входом рециркулятора, выход которого соединен с входом вычислителя быстрого преобразования Фурье, выход которого соединен с первым входом блока перемножения. Дополнительно введены: блок обнуления отрицательных частот, входом которого является выход вычислителя быстрого преобразования Фурье, а выход соединен с первым входом блока перемножения; постоянное запоминающее устройство, выход которого соединен со вторым входом блока перемножения, выход которого является входом блока вычисления двухмерного обратного быстрого преобразования Фурье, выход которого соединен с входом вычислителя квадрата модуля, выход которого является выходом устройства; управляющее устройство, выходы которого подсоединены к управляющим входам аналого-цифрового преобразователя, вычислителя быстрого преобразования Фурье, перемножителя, блока вычисления двухмерного обратного быстрого преобразования Фурье, вычислителя квадрата модуля. Технический результат: повышение помехоустойчивости обнаружения сигналов на фоне реверберационной помехи. 3 ил.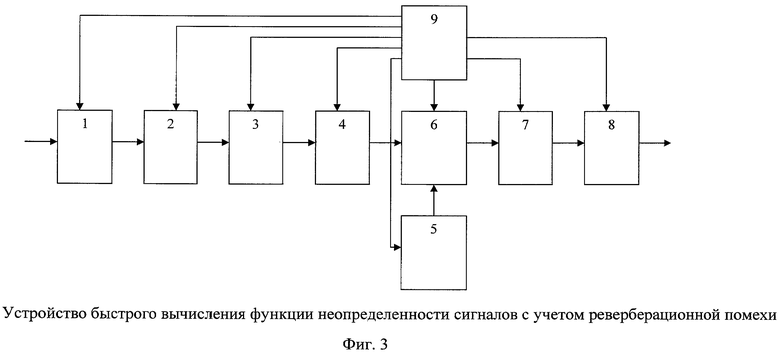

Устройство для вычисления функции неопределенности сигнала с учетом реверберационной помехи, содержащее аналого-цифровой преобразователь, на вход которого поступает входная реализация, а выход которого соединен с входом рециркулятора, выход которого соединен с входом вычислителя быстрого преобразования Фурье, выход которого соединен с первым входом блока перемножения, отличающееся тем, что дополнительно введены: блок обнуления отрицательных частот, входом которого является выход вычислителя быстрого преобразования Фурье, а выход соединен с первым входом блока перемножения; постоянное запоминающее устройство, выход которого соединен со вторым входом блока перемножения, выход которого является входом блока вычисления двухмерного обратного быстрого преобразования Фурье, выход которого соединен с входом вычислителя квадрата модуля, выход которого является выходом устройства; управляющее устройство, выходы которого подсоединены к управляющим входам аналого-цифрового преобразователя, вычислителя быстрого преобразования Фурье, перемножителя, блока вычисления двухмерного обратного быстрого преобразования Фурье, вычислителя квадрата модуля.