Изобретение относится к области криптографических систем, а более точно к области систем, использующих цифровую подпись, и может быть использовано в электронных системах массового обслуживания.
Цифровая подпись широко используется на практике и играет роль, аналогичную роли обычной рукописной подписи. Преимущества цифровой подписи состоят в том, что ее достоверность легко проверяема, ее подделка весьма затруднительна, и, кроме того, цифровая подпись легко может быть передана по телекоммуникационным каналам. В системах, использующих цифровую подпись, имеют дело с данными, которые располагаются на подходящих материальных носителях и могут быть представлены цифровым образом.
В схеме RSA, называемой так по первым буквам имен ее изобретателей (Rivest, Shamir, Adleman), используют представление данных целыми числами из некоторой системы вычетов по модулю целого числа N, называемого RSA-модулем. В качестве системы вычетов обычно используют целые числа от 0 до N-1. Понятия, связанные со схемой RSA ([1], стр. 285, 433; [2], стр. 466-474), могут быть снабжены, для определенности, префиксом RSA, например, RSA-подпись, RSA-шифрование, RSA-ключ, RSA-экспонента и т.п.
Данные S удовлетворяют свойству цифровой RSA-подписи для данных М по отношению к RSA-ключу с модулем N и экспонентой E или, иными словами, являются цифровой RSA-подписью для данных M, если M ≡ SE(modN). При этом под RSA-ключом имеются в виду произвольные данные, определяющие модуль и экспоненту, экспонента представляет собой некоторое целое число, а запись A ≡ B (modN) означает, что A и B сравнимы по модулю N, то есть что целое число (A - B) делится нацело на N.
Известен способ изготовления цифровой RSA-подписи [3], в котором цифровую RSA-подпись для данных М изготавливают RSA-шифрованием данных М, при котором в качестве шифровального ключа используют секретный RSA-ключ подписывающей стороны, соответствующий открытому RSA-ключу с модулем N и экспонентой E. При этом под RSA-шифрованием имеется в виду обработка данных X, в результате которой получают данные Y, удовлетворяющие соотношению Y ≡ XC(modN), где С и N, соответственно, экспонента и модуль шифровального RSA-ключа. Под соответствием двух RSA-ключей имеется в виду возможность проверки цифровой RSA-подписи, изготовленной одним RSA-ключом, с помощью другого RSA-ключа или, что то же самое, возможность расшифровки данных, зашифрованных одним ключом, посредством другого ключа. Соответствие RSA-ключей с экспонентами A и B и модулем N обеспечено условием A•B ≡ 1(modϕ(N)), где ϕ(N) - число вычетов, взаимно простых с N.
Однако изготовление цифровой RSA-подписи для исходных данных М непосредственным RSA-шифрованием исходных данных секретным RSA-ключом подписывающей стороны не обеспечивает приватности подателей, так как предназначенные для подписания исходные данные доступны подписывающей стороне при изготовлении подписи. Это пояснено в [4], где введена концепция изготовления цифровой подписи вслепую, предназначенная для преодоления этого недостатка.
Известен способ изготовления вслепую цифровой RSA-подписи [5], в котором податель, желающий получить цифровую RSA-подпись для исходных данных М, выбирает рандомизированный маскировочный ключ R и создает замаскированные данные М' в соответствии с формулой M′ ≡ RE•M(modN), где E - экспонента, a N - модуль открытого RSA-ключа. Замаскированные данные предоставляются подписывающей стороне, которая возвращает подателю цифровую RSA-подпись S' для замаскированных данных. Податель завершает изготовление цифровой RSA-подписи S для исходных данных демаскировкой полученной цифровой RSA-подписи для замаскированных данных, которую проводит в соответствии с формулой S ≡ S′•R-1(modN). Известный способ обеспечивает непрослеживаемость, то есть практическую невозможность для подписывающей стороны, получившей впоследствии подписи многих исходных данных, установить соответствие между этими подписями и обработанными замаскированными данными. Однако известный способ не позволяет изготовить вслепую цифровую RSA-подпись без предварительного знания вида подписи, так как экспонента E открытого ключа, определяющая вид подписи, используется при создании замаскированных данных.
Известен способ изготовления вслепую неожидаемой цифровой RSA-подписи [6] , который является наиболее близким аналогом к предлагаемому изобретению и выбран в качестве прототипа. В этом способе используют набор допустимых открытых RSA-экспонент E1,..., Ek и набор данных (g1,...,u), названных генераторами. Для каждого генератора gj публикуют цифровые RSA-подписи Sij, соответствующие каждой допустимой открытой RSA-экспоненте Ei. Податель выбирает в качестве рандомизированного маскировочного ключа R набор (k1,...,ku) и создает замаскированные данные М' в соответствии с формулой M'=M•g1 k1... gu ku(mod N), где N модуль открытого RSA-ключа. Замаскированные данные M' предоставляют подписывающей стороне, которая выбирает вид подписи, то есть выбирает ту допустимую открытую RSA-экспоненту Ei, которой будет соответствовать изготавливаемая цифровая RSA-подпись. Цифровую RSA-подпись S' для замаскированных данных, соответствующую выбранной открытой RSA-экспоненте Ei, вместе с информацией о выбранной открытой RSA-экспоненте Ei, предоставляют подателю. Податель получает цифровую RSA-подпись S для исходных данных демаскировкой S', которую проводят в соответствии с формулой S ≡ S′•S
Непрослеживаемость в известном способе изготовления вслепую неожидаемой цифровой RSA-подписи определенными свойствами генераторов по отношению к секретным RSA-ключам, в связи с чем используется тестирование пригодности генераторов методом "cut and choose" Подпись в известном способе называется неожидаемой, так как податель, в момент предоставления подписывающей стороне замаскированных данных, не знает вида изготавливаемой подписи, то есть той открытой RSA-экспоненты, которой будет соответствовать изготавливаемая подпись.
Недостатки известного способа состоят в ограничении количества видов изготавливаемой RSA-подписи, что снижает ее неожидаемость, в росте вероятности ошибок при изготовлении подписи и в замедляющем воздействии количества видов подписи на скорость ее изготовления. Указанные недостатки обусловлены необходимостью осуществлять демаскировку с помощью растущего пропорционально количеству видов подписи объема данных, которые, в свою очередь, требуют дополнительных ресурсов и времени для их хранения и обработки. Кроме того, известный способ имеет недостаточную достоверность непрослеживаемости, так как проверка пригодности сообщенных подписывающей стороной данных, в частности генераторов, производится третьей стороной, а не подателем непосредственно.
Известно устройство для изготовления вслепую цифровой RSA-подписи [5]. Однако этого устройства не достаточно для изготовления для изготовления вслепую неожидаемой цифровой RSA-подписи.
Известно устройство для изготовления вслепую неожидаемой цифровой RSA-подписи [6], наиболее близкое к заявляемому устройству и выбранное в качестве прототипа. Известное устройство состоит из блока выбора маскировочного ключа, включающего датчик случайных чисел, блока маскировки, блока подписи и блока демаскировки. Блок маскировки имеет входы исходных данных и маскировочного ключа и содержит модулярный экспоненциатор, к модульному входу которого подсоединен модульный вход блока маскировки, а к экспонентному входу которого подсоединен вход маскировочного ключа блока маскировки. Блок подписи имеет вход секретного ключа и вход данных подписи, соединенный с выходом блока маскировки. Блок демаскировки имеет модульный вход, экспонентный вход, вход маскировочного ключа, вход данных демаскировки, соединенный с выходом блока подписи, и выход для вывода цифровой RSA-подписи для исходных данных.
Недостатки известного устройства состоят в том, что оно не позволяет при изготовлении вслепую цифровой RSA-подписи использовать неограниченное количество видов подписи, что снижает неожидаемость изготавливаемой цифровой RSA-подписи, его использование приводит к росту вероятности ошибок при изготовлении подписи и к замедляющему воздействию количества видов подписи на скорость ее изготовления, что обусловлено необходимостью вводить в демаскирующий блок данные, поиск которых требует времени, растущего пропорционально количеству видов подписи.
Основной задачей, решаемой вариантами заявленного изобретения, является создание таких способа изготовления вслепую цифровой RSA-подписи и устройства для его реализации, которые обеспечили бы непрослеживаемость и высокую неожидаемость при изготовления цифровой RSA-подписи, а также допускали бы быстрое изготовление вслепую цифровой RSA-подписи при сравнительно небольших ресурсах.
Единый для всех предложенных вариантов заявленного изобретения технический результат, достигаемый при их реализации, состоит в том, что при изготовлении вслепую неожидаемой цифровой RSA-подписи возможно использование неограниченного количества видов подписи, не требуются растущие в зависимости от количества возможных видов подписи технические ресурсы, хранилища больших объемов данных и поиск в них, что приводит к ускорению и повышению надежности изготовления вслепую цифровой RSA-подписи. Помимо этого, повышается достоверность непрослеживаемости за счет того, что свойства данных, обеспечивающих непрослеживаемость, могут быть, в некоторых из заявленных вариантов, протестированы непосредственно самим подателем.
Принципиальное отличие заявленного изобретения от известного уровня техники и прототипа заключается в существенно ином создании замаскированных данных, что обуславливает другие существенные отличия, необходимые для получения указанного технического результата.
Заявленный способ изготовления вслепую цифровой RSA-подписи предназначен исключительно для аппаратной или компьютерной реализации, так как сама цифровая RSA-подпись реализуется только на аппаратной или компьютерной основе [3].
В описании изобретения используются известные устройства, реализующие основные арифметические функции и основные функции модулярной арифметики. Такие устройства могут работать с данными, представляющими целые числа подходящей разрядности. Для уточнения терминологии далее описана функциональность используемых устройств. Под модулярным умножителем имеется в виду устройство с модульным и двумя аргументными входами, причем если на модульный вход подано целое число N, а на аргументные входы поданы целые числа X, Y, то на выходе появляется целое число Z такое, что Z ≡ X•Y(modN). Под модулярным инвертором имеется в виду устройство с модульным и аргументным входами, причем если на модульный вход подано целое число N, а на аргументный вход подано целое число X, взаимно простое с N, то на выходе появляется целое число Y такое, что X•Y ≡ 1(modN). Под модулярным вычислителем частного имеется в виду устройство с модульным входом и входами делимого и делителя, причем если на модульный вход подано целое число N, на вход делимого подано целое число X, а на вход делителя подано целое число Y, взаимно простое с N, то на выходе появляется целое число Z такое, что Z•Y ≡ X(modN). Под модулярным экспоненциатором имеется в виду устройство с модульным, базовым и экспонентным входами, причем если на модульный вход подано целое число N, на базовый вход подано целое число X, а на экспонентный вход подано целое число E, то на выходе появляется целое число Z такое, что Z ≡ XE(modN). Под тестером взаимной простоты имеется в виду устройство с двумя входами, причем если на входы поданы целые числа A и B, то на выходе появляется логическое значение "Истина", если наибольший общий делитель A и B равен единице, и логическое значение "Ложь" в ином случае.
В описании изобретения также используются понятие рандомизированных данных. Рандомизация данных, то есть внесение элемента случайности в их выбор, может быть осуществлена, например, с помощью датчика случайных чисел или иным способом. При этом под датчиком случайных чисел имеется в виду устройство, на выходе которого появляются данные подходящей разрядности, предпочтительно непредсказуемые для стороны, не контролирующей работу такого устройства. Такие устройства хорошо известны. В частности, в качестве датчиков случайных чисел могут использоваться датчики "псевдослучайных" чисел.
Указанный выше технический результат при реализации изобретения достигается тем, что способ изготовления вслепую цифровой RSA-подписи по первому варианту, заключающийся в выборе тестированием секретных множителей и соответствующего им RSA- модуля, выборе открытой RSA-экспоненты и соответствующего секретного RSA-ключа, произвольном выборе исходных данных, выборе рандомизированного маскировочного ключа, выборе шифровального RSA-ключа, модуль которого соответствует выбранному RSA-модулю, а экспонента которого соответствует выбранному рандомизированному маскировочному ключу, которым осуществляют RSA-шифрование при создании замаскированных данных, для которых создают цифровую RSA-подпись, демаскировки созданной цифровой RSA-подписи для замаскированных данных, которую производят введением ее, рандомизированного маскировочного ключа, RSA-модуля и открытой RSA-экспоненты в демаскирующий преобразователь, выходные данные которого принимают в качестве цифровой RSA-подписи для выбранных исходных данных, отличается от известного способа изготовления вслепую неожидаемой цифровой подписи, выбранного в качестве прототипа, тем, что при создании замаскированных данных осуществляют RSA-шифрование выбранных исходных данных, при демаскировке созданной цифровой RSA-подписи для замаскированных данных дополнительно вводят в демаскирующий преобразователь выбранные исходные данные, при выборе секретных множителей осуществляют их дополнительное тестирование на несравнимость с единицей по модулю делителей в задаваемом диапазоне и попарно на одновременную сравнимость с единицей по модулю произвольных нечетных делителей, на основе тестирования на несравнимость с единицей по модулю делителей в задаваемом диапазоне дополнительно выбирают маскирующий множитель, рандомизированный маскировочный ключ выбирают взаимно простым относительно выбранной открытой RSA-экспоненты и кратным выбранному маскирующему множителю.
Указанный выше технический результат в частных случаях конкретной реализации может достигаться, кроме того, тем, что при выборе секретных множителей дополнительное попарное тестирование секретных множителей на одновременную сравнимость с единицей по модулю произвольных нечетных делителей осуществляют сравнением значения наибольшего общего делителя уменьшенных на единицу секретных множителей с целым числом, равным двум.
Более того, при выборе секретных множителей в качестве критерия их отбора принимают несравнимость с единицей по модулю тех делителей из задаваемого диапазона, которые не являются делителями выбранного маскирующего множителя.
Помимо этого, маскирующий множитель выбирают кратным тем делителям из задаваемого диапазона, по модулю которых сравним с единицей, по меньшей мере, один из выбранных секретных множителей.
В частности, при выборе секретных множителей их отбор производят по наперед заданной вероятности отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных.
Кроме того, нижнюю границу задаваемого диапазона выбирают равной двум, а верхнюю границу задаваемого диапазона выбирают по наперед заданной вероятности отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных.
В частности, в качестве маскирующего множителя выбирают целое число, равное двум.
Помимо этого, выбор рандомизированного маскировочного ключа осуществляют посредством датчика случайных чисел. Более того, выбор рандомизированного маскировочного ключа производят тестированием четности выходных данных датчика случайных чисел и тестированием взаимной простоты выходных данных датчика случайных чисел относительно открытой RSA-экспоненты.
В частности, при демаскировке созданной цифровой RSA-подписи для замаскированных данных выбранные исходные данные, которые предварительно введены в демаскирующий преобразователь, подают на один из базовых входов содержащегося в нем модулярного мультипликативного евклидова преобразователя (ММЕП), на другой базовый вход которого подают созданную цифровую RSA-подпись для замаскированных данных, предварительно введенную в демаскирующий преобразователь, выбранный рандомизированный маскировочный ключ вводят на экспонентный вход ММЕП, соответствующий базовому входу, на который подают выбранные исходные данные, а открытую RSA- экспоненту вводят на экспонентный вход ММЕП, соответствующий базовому входу, на который подают созданную цифровую RSA-подпись для замаскированных данных.
Под модулярным мультипликативным евклидовым преобразователем (ММЕП) имеется в виду устройство, имеющее модульный вход, два базовых входа, два соответствующих экспонентных входа и один выход, причем если на модульный вход ММЕП подано целое положительное число N, на один из базовых входов подано взаимно простое с N целое число X, на соответствующий ему экспонентный вход подано целое число A, на другой базовый вход подано взаимно простое с N целое число Y, а на соответствующий ему экспонентный вход подано целое число B, причем целые числа A и B взаимно просты, то на выходе появляется целое число Z такое, что Z ≡ XCYD(modN), где С и D - произвольные целые числа, удовлетворяющие соотношению A•С + B•D = 1. В литературе ([7], стр. 367-368) имеются сведения, достаточные для создания ММЕП специалистами среднего уровня. Для настоящего изобретения существенным является функция, выполняемая ММЕП, а не его конкретная реализация. Тем не менее для подтверждения реализуемости далее в примерах 8 и 10 приведен пример конкретной реализации ММЕП и его работы, а в приведенном ниже примере 1 реализации способа изготовления вслепую цифровой RSA-подписи по первому варианту дано краткое пояснение осуществления демаскировки частным случаем ее реализации с использованием ММЕП.
Сущность способа изготовления вслепую цифровой RSA-подписи по первому варианту состоит в том, что подписывающая сторона выбирает в качестве секретных множителей простые числа P и Q, как и в прототипе, но удовлетворяющие дополнительно условию Н.О.Д.(Р-1, Q- 1) = 2 (сокращение Н.О.Д.(X, Y) используется для обозначения наибольшего общего делителя целых чисел X и Y). Выбор RSA-модуля N, открытой RSA-экспоненты E осуществляют так же, как и прототипе. RSA-модуль N и открытая RSA-экспонента E сообщается заинтересованным сторонам. Кроме того, подписывающая сторона сообщает подателям маскирующий множитель G, который выбирает кратным всем делителям Р-1 и Q-1 в задаваемом диапазоне. Податель, желая создать подпись на исходных данных М, выбирает в качестве рандомизированного маскировочного ключа целое число R, кратное W, и такое, что Н. О. Д (R, E) = 1, и производит маскировку исходных данных М, создавая на их основе замаскированные данные М' в соответствии с формулой M′ ≡ MR(modN). Ниже в тексте описания термин "рандомизированный маскировочный ключ" может быть для краткости заменен термином "маскировочный ключ" в тех случаях, когда не требуется подчеркнуть происхождение маскировочного ключа. Цифровую RSA-подпись S' для данных М' изготавливают так же, как и прототипе, то есть в соответствии с формулой S′ ≡ (M′)D(modN), где D - секретная RSA-экспонента, соответствующая открытой RSA-экспоненте E. Податель, получив данные S', завершает изготовление цифровой RSA- подписи S для исходных данных M демаскировкой S' в соответствии с формулой S′ ≡ (S′)AMB(modN), где A и B связаны соотношением A•R + B•E = 1. В частности, податель может сначала изготовить целые числа A и B, в соответствии с хорошо известным обобщенным алгоритмом Евклида, а затем данные S. Разумеется, податель известными способами может проверить, что изготовленная цифровая RSA-подпись S удовлетворяет свойству подписи для исходных данных М.
Единая совокупность признаков первого варианта заявленного способа, перечисленных выше, связана причинно-следственной связью с ранее изложенным техническим результатом изобретения, заключающимся в том, что при изготовлении вслепую неожидаемой цифровой RSA-подписи возможно использование неограниченного количества видов подписи; кроме того, не требуются растущие в зависимости от количества возможных видов подписи ресурсы, хранилища больших объемов данных и поиск в них, что, в свою очередь, приводит к ускорению и повышению надежности способа изготовления вслепую цифровой RSA-подписи.
Указанный выше технический результат при осуществлении способа изготовления цифровой RSA-подписи по первому варианту достигается, в частности, тем, что при выборе секретных множителей верхнюю границу U задаваемого диапазона выбирают по наперед заданной вероятности W отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных. Иными словами, речь идет о вероятности такого неудачного выбора подателем исходных данных, который приведет к специфическому виду замаскированных данных и, тем самым, не обеспечит непрослеживаемости. Выбор W = 10-8 обеспечивает практически полную непрослеживаемость. Для оценки того, какой достаточно взять верхнюю границу U, обеспечивающей необходимую вероятность W, предположим, что P и Q - различные нечетные простые числа, N = P•Q, G - маскирующий множитель, кратный всем общим делителям Р-1 и Q-1 и кратный всем делителям каждого из чисел P-1 и Q-1, не превосходящим некоторой границы U. Предположим, что замаскированные данные М' связаны с М соотношением M′ ≡ XGRmodN, где R - случайно выбранное число. Вероятность W того, что для случайно выбранных данных М множество всех замаскированных данных, созданных на основе М, отличается от множества G-тых степеней по модулю N равна 1 - V. При этом V - вероятность того, что множество всех замаскированных данных, которые могут быть созданы на основе случайных и равномерно распределенных среди обратимых вычетов по модулю N исходных данных М, то есть множество обратимых вычетов вида МR (mod N), где R пробегает все целые числа, кратные G, совпадает с группой Z всех обратимых вычетов вида CG (mod N), где С пробегает все обратимые вычеты по модулю N. Вероятность V не меньше, чем произведения чисел (1-L-1), где L пробегает простые делители (P - 1)(Q - 1), большие U. Тем самым вероятность W меньше, чем Log(N)/[U•Log(U + 1)]. Кроме того, оценка W дает и оценку вероятности W1 того, что для случайных исходных данных X, равномерно распределенных среди обратимых вычетов по модулю N, и случайных независимых данных Y1 и Y2, равномерно распределенных среди тех обратимых вычетов по модулю N, которые являются G-тыми степенями по модулю N, вероятность получения Y1 маскировкой X равна вероятности получения Y2 маскировкой X. Близость W1 к 1 также обеспечивает непрослеживаемость и, следовательно, вероятность W1 определяет уровень маскировки.
Кроме того, в качестве секретных множителей подписывающая сторона может взять простые числа вида 2L + 1, где L также простое число.
Ниже приведен пример конкретной реализации способа изготовления вслепую цифровой RSA-подписи по первому варианту.
Пример 1
Для простоты изложения всех приведенных здесь и далее примеров секретные множители выбраны состоящими из небольшого количества цифр (в реальных системах цифровой RSA-подписи используются секретные множители, состоящие из многих десятков цифр), в частности, в данном примере, трехзначными.
При выборе первого секретного множителя подписывающая сторона получает посредством датчика случайных чисел начальные пробные данные P и тестирует следующие их свойства: (а) нечетность; (б) несравнимость с 1 по модулю 4 и всех простых нечетных чисел, не превосходящих 10; (в) простоту. Если пробные данные не проходят хотя бы один из этих тестов, то они бракуются и начинается тестирование очередных пробных данных, полученных например, добавлением 1 к предыдущим пробным данным. Эта процедура продолжается до тех пор, пока очередные пробные данные не пройдут всех тестов и будут приняты, в этом случае, в качестве первого секретного множителя. Допустим, что в качестве начальных пробных данных выбраны данные P = 414. Они не выдерживают теста на нечетность и бракуются. Очередные пробные данные P = 415 не выдерживают теста на несравнимость с единицей по модулю 3 и также бракуются. Пробные данные 416 и 418 будут забракованы тестом на нечетность, пробные данные 417 будут забракованы тестом на несравнимость с 1 по модулю 4, а очередные пробные данные P = 419 выдержат все тесты и будут приняты в качестве первого секретного множителя. После этого подписывающая сторона выбирает аналогичным образом второй секретный множитель. Для этого подписывающая сторона выбирает посредством датчика случайных чисел начальные пробные данные Q и тестирует их свойства (а), (б), (в), указанные выше, а если пробные данные выдерживают все эти тесты, то осуществляют дополнительное попарное тестирование секретных множителей на одновременную сравнимость с единицей по модулю произвольных нечетных делителей, где термин "попарно" означает, что такое тестирование осуществляют для каждой пары секретных множителей. В частности, такое тестирование может быть осуществлено сравнением значения наибольшего общего делителя уменьшенных на единицу секретных множителей с целым числом, равным двум. Так как в этом примере имеется всего одна пара секретных множителей (P, Q), то для этой пары тестируется следующее свойство (г) Н.О.Д. (Р-1, Q-1) = 2. Если очередные пробные данные выдерживают и этот тест, то их принимают в качестве второго секретного множителя и на этом заканчивают выбор секретных множителей. Допустим, что в качестве начальных пробных данных выбраны данные Q = 857. Начальные пробные данные 857 бракуются тестом на несравнимость с 1 по модулю 4, очередные пробные данные 858 бракуются тестом на нечетность. Следующие пробные данные 859 бракуются тестом (б), и начинается тестирование очередных пробных данных 860. Пробные данные 860 и 862 бракуются тестом на четность, а пробные данные 861 бракуются тестом на несравнимость с 1 по модулю 4. В итоге пробные данные Q = 863 пройдут все тесты и будут приняты в качестве второго секретного множителя.
После этого подписывающая сторона создает RSA-модуль N, например, посредством умножителя подходящей разрядности, как произведение секретных множителей. В этом примере N = P•Q = 419•863 = 361597. В качестве открытой RSA-экспоненты E подписывающая сторона выбирает произвольное число, взаимно простое с P-1 и Q-1, например E = 3. После этого RSA-модуль 361597 и открытая RSA-экспонента E = 3 сообщаются всем заинтересованным потенциальным подателям.
Предположим, что податель желает изготовить вслепую для подписывающей стороны цифровую RSA-подпись некоторых исходных данных M в диапазоне от 0 до N-1. Для определенности рассмотрим М = 123456. Податель посредством датчика случайных чисел выбирает маскировочный ключ R, размер которого сопоставим с размером RSA-модуля. Например, пусть R= 901. Проверив четность маскировочного ключа R и взаимную простоту R относительно открытой RSA-экспоненты E = 3, податель приступает к созданию замаскированных данных М'. A именно, в качестве замаскированных данных принимают результат RSA-шифрования RSA-ключом (N, R) = (361597, 901) исходных данных М = 123456. Это RSA-шифрование можно произвести модулярным экспоненциатором, на модульный вход которого подают RSA-модуль, N = 361597, на базовый вход которого подают исходные данные М = 123456, на экспонентный вход которого подают маскировочный ключ R = 901, а выходные данные которого принимают в качестве замаскированных данных М'. На выходе модулярного экспоненциатора получим цифровые данные MR(modN) ≡ (123456)901(mod361597) = 237367. Итак, M'= 237367.
Подписывающая сторона до создания цифровой RSA-подписи S для замаскированных данных М' создает секретный ключ (N, D), где экспонента D секретного RSA-ключа D создается посредством модулярного инвертора, на модульным вход которого подается ϕ(N) = (P-1)•(Q-1) = 418•862 = 360316, на аргументный вход которого подается выбранная открытая RSA-экcпoнентa E = 3, а на выходе которого появляется D ≡ E-1(modN) = 3-1(mod360316) = 240211. Далее подписывающая сторона так же, как и прототипе, создает цифровую RSA-подпись S' для замаскированных данных М'. Это может быть сделано посредством модулярного экспоненциатора, на модульный вход которого подают RSA-модуль N = 361597, на базовый вход которого подают замаскированные данные М' = 237367, на экспонентный вход которого подают экспоненту секретного RSA-ключа D = 240211, а выходные данные которого принимают в качестве цифровой RSA-подписи S' для замаскированных данных М'. Тем самым 
Получив цифровую RSA-подпись S' для замаскированных данных М податель осуществляет демаскировку данных S' и, тем самым, создает цифровую RSA-подписи S для исходных данных М. Для этого податель подает данные S' = 88275 на первый базовый вход модулярного мультипликативного евклидова преобразователя (ММЕП), а исходные данные М = 123456 на второй базовый вход ММЕП, маскировочный ключ R = 901 на первый экспонентный вход ММЕП, открытую экспоненту E = 3 на второй экспонентный вход ММЕП, а RSA- модуль N = 361597 на модульный вход ММЕП. На выходе появляются данные S = 88275•278670 (mod 361597) = 150340, которые и являются цифровой RSA-подписью для исходных данных М = 123456.
В качестве других частных случаев способа по первому варианту отмечается возможность реализации в виде многих иных комбинаций зависимых пунктов 2-11, а также возможность шифрования, дешифрования и перекодировки данных при их передаче от подателя к подписывающей стороне и наоборот, которые не меняют сущности заявленного изобретения. Разумеется, правильность изготовленной цифровой RSA-подписи может быть проверена известными способами.
Кроме того, то, что податели могут убедиться в том, наибольший общий делитель уменьшенных на единицу секретных множителей равен двум, а также в том, что сообщенный подписывающей стороной маскирующий множитель G действительно кратен всем делителям уменьшенных на единицу секретных множителей в указанном ей диапазоне без раскрытия подписывающей стороной секретных множителей с помощью известного метода "cut and choose". А именно, подписывающая сторона выбирает первоначально большое количество наборов RSA-модулей и маскирующих множителей и опубликовывает их. Представитель подателей выбирает все наборы, кроме одного, после чего подписывающая сторона раскрывает для каждого выбранного представителем подателей набора соответствующие секретные множители. Имея секретные множители, представитель подателей убеждается в правильности выбора секретных и маскирующих множителей в выбранных им наборах. Тем самым, представитель подателей косвенным образом убеждается и в правильности выбора секретных множителей и маскирующего множителя в невыбранном им наборе, а подписывающая сторона использует этот оставшийся набор при изготовлении подписи.
В качестве исходных данных податель может выбрать имеющуюся у него цифровую RSA-подпись некоторых более ранних исходных данных и тем самым получить цифровую RSA-подпись более ранних исходных данных, соответствующую произведению открытой RSA-экспоненты, соответствующей уже имеющейся подписи, и используемой открытой RSA- экспоненты.
После изготовления цифровой RSA-подписи для исходных данных, соответствующей открытой RSA-экспоненте E, податель может без помощи подписывающей стороны изготовить цифровую RSA-подпись для исходных данных, соответствующую произвольной открытой RSA-экспоненте, являющейся делителем E.
Указанный выше технический результат при реализации изобретения достигается тем, что способ изготовления вслепую цифровой RSA-подписи по второму варианту, заключающийся в выборе тестированием секретных множителей и соответствующего им RSA-модуля, выборе, по меньшей мере, одной открытой RSA-экспоненты, выборе исходных данных, выборе рандомизированного маскировочного ключа, выборе шифровального RSA-ключа, модуль которого соответствует выбранному RSA-модулю, а экспонента которого соответствует выбранному рандомизированному маскировочному ключу, которым осуществляют RSA-шифрование при создании замаскированных данных, произвольном выборе секретного RSA-ключа, соответствующего выбранным секретным множителям и выбранным открытым RSA-экспонентам, и создании соответствующей ему цифровой RSA-подписи для замаскированных данных, демаскировки созданной данной цифровой RSA-подписи для замаскированных данных, которую производят введением ее, рандомизированного маскировочного ключа, RSA-модуля и открытой RSA-экспоненты, соответствующей секретному RSA-ключу, использованному при создании цифровой RSA-подписи для замаскированных данных, в демаскирующий преобразователь, выходные данные которого принимают в качестве цифровой RSA-подписи для выбранных исходных данных, отличается от известного способа изготовления вслепую неожидаемой цифровой подписи, выбранного в качестве прототипа, тем, что при создании замаскированных данных осуществляют RSA-шифрование выбранных исходных данных, произвольный выбор секретного ключа осуществляют на основе произвольного выбора кратностей выбранных открытых RSA- экспонент, при демаскировке созданной цифровой RSA-подписи для замаскированных данных дополнительно вводят в демаскирующий преобразователь выбранные исходные данные, при выборе секретных множителей осуществляют их дополнительное тестирование на несравнимость с единицей по модулю делителей в задаваемом диапазоне и попарно на одновременную сравнимость с единицей по модулю произвольных нечетных делителей, на основе тестирования на несравнимость с единицей по модулю делителей в задаваемом диапазоне дополнительно выбирают маскирующий множитель, рандомизированный маскировочный ключ выбирают взаимно простым относительно выбранных открытых RSA-экспонент и кратным выбранному маскирующему множителю.
Указанный выше технический результат в частных случаях конкретной реализации может достигаться, кроме того, тем, что при выборе секретных множителей дополнительное попарное тестирование секретных множителей на одновременную сравнимость с единицей по модулю произвольных нечетных делителей осуществляют сравнением значения наибольшего общего делителя уменьшенных на единицу секретных множителей с целым числом, равным двум.
Более того, при выборе секретных множителей в качестве критерия их отбора принимают несравнимость с единицей по модулю тех делителей из задаваемого диапазона, которые не являются делителями выбранного маскирующего множителя.
Помимо этого, маскирующий множитель выбирают кратным тем делителям из задаваемого диапазона, по модулю которых сравним с единицей, по меньшей мере, один из выбранных секретных множителей.
В частности, отбор секретных множителей производят по наперед заданной вероятности отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных.
Кроме того, нижнюю границу задаваемого диапазона выбирают равной двум, а верхнюю границу задаваемого диапазона выбирают по наперед заданной вероятности отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных.
В частности, в качестве маскирующего множителя выбирают целое число, равное двум.
Помимо этого, выбор рандомизированного маскировочного ключа осуществляют посредством датчика случайных чисел. Более того, выбор рандомизированного маскировочного ключа производят тестированием четности выходных данных датчика случайных чисел и тестированием взаимной простоты выходных данных датчика случайных чисел относительно выбранных открытых RSA-экспонент.
В частности, при демаскировке созданной цифровой RSA-подписи для замаскированных данных выбранные исходные данные, которые предварительно введены в демаскирующий преобразователь, подают на один из базовых входов содержащегося в нем модулярного мультипликативного евклидова преобразователя (ММЕП), на другой базовый вход которого подают созданную цифровую RSA-подпись для замаскированных данных, предварительно введенную в демаскирующий преобразователь, выбранный рандомизированный маскировочный ключ вводят на экспонентный вход ММЕП, соответствующий базовому входу, на который подают выбранные исходные данные, а предварительно введенную в демаскирующий преобразователь открытую RSA-экспоненту вводят на экспонентный вход ММЕП, соответствующий базовому входу, на который подают созданную цифровую RSA-подпись для замаскированных данных.
Для наглядности в приведенном ниже примере реализации способа изготовления вслепую цифровой RSA-подписи по второму варианту дано краткое пояснение осуществления демаскировки частным случаем ее реализации с использованием ММЕП.
Сущность способа изготовления вслепую цифровой RSA-подписи по второму варианту состоит, в основном, в том, что и указанная выше сущность заявляемого способа по первому варианту. Отличие состоит в том, что при реализации заявленного способа по второму варианту подписывающая сторона выбирает несколько открытых RSA-экспонент E1,...Ek. Под кратностью открытой RSA-экспоненты Ej, имеется в виду произвольное неотрицательное целое число rj. Имеется в виду, что при выборе секретного ключа на основе выбора кратностей открытых RSA-экспонент берут тот секретный ключ, секретная экспонента D которого соответствует произведению секретных экспонент Dj rj. При этом Dj - секретная экспонента, соответствующая открытой RSA- экспоненте Ej. Данный способ изготовления цифровой RSA-подписи обеспечивает непрослеживаемость по тем же причинам, что и в способе изготовления цифровой RSA-подписи по первому варианту.
Единая совокупность признаков второго варианта заявленного способа, перечисленных выше, связана причинно-следственной связью с ранее изложенным результатом изобретения, заключающимся в том, что при изготовлении вслепую неожидаемой цифровой RSA-подписи возможно использование неограниченного количества видов подписи; кроме того, не требуются растущие в зависимости от количества возможных видов подписи ресурсы, хранилища больших объемов данных и поиск в них, что, в свою очередь, приводит к ускорению и повышению надежности способа изготовления вслепую цифровой RSA-подписи.
Ниже приведен пример конкретной реализации способа изготовления вслепую цифровой RSA-подписи по второму варианту.
Пример 2
Подписывающая сторона выбирает секретные множители P, Q и создает RSA-модуль N, так же как и в примере 1. Итак, пусть P=419, Q=863, a N = 361597. B качестве открытых RSA-экспонент подписывающая сторона выбирает произвольные числа, взаимно простые c P-1 Q-1, например, E1 = 3 и E2 = 5. После этого RSA-модуль и открытые RSA-экспоненты E1 = 3 и E2 = 5 сообщаются всем заинтересованным потенциальным подателям.
Предположим, что податель, как в примере 1, выбрал исходные данные М = 123456, маскировочный ключ R = 901 и создал замаскированные данные М' = 237367.
Подписывающая сторона до создания цифровой RSA-подписи S' для замаскированных данных М' произвольно выбирает кратности созданных открытых RSA-экспонент. В данном примере, подписывающая сторона выбирает кратность r1 открытой RSA-экспоненты E1 = 3 и кратность r2 открытой RSA-экспоненты E2 = 5, например, r1 = 6 и r2 = 4 (выбор этих кратностей определяет вид будущей цифровой RSA- подписи и диктуется обстоятельствами, не существенными для настоящего изобретения). После этого подписывающая сторона создает секретный ключ (N, D), где экспонента D секретного RSA-ключа создается посредством модулярных экспоненциаторов и модулярного умножителя в соответствии с формулой D ≡ D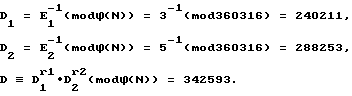
Далее подписывающая сторона создает цифровую RSA-подпись S' для замаскированных данных М', как в примере 1, и получает S' = (M')D mod N = 114272.
Податель завершает изготовление цифровой RSA-подписи S для исходных данных М демаскировкой данных S' как в примере 1, за исключением того, что на основе использованных подписывающей стороной кратностей открытых RSA-экспонент r1 = 6 и r2 = 4 податель предварительно создает открытую экспоненту E в соответствии с формулой E = E1 r1 • E2 r2. Тем самым в данном примере E = 36 • 54 = 455625. Для осуществления демаскировки податель подает данные S' = 114272 на первый базовый вход модулярного мультипликативного евклидова преобразователя (ММЕП), а исходные данные М = 123456 на второй базовый вход ММЕП, маскировочный ключ R = 901 на первый экспонентный вход ММЕП, открытую экспоненту E = 455625 на второй экспонентный вход ММЕП, а RSA-модуль N = 361597 на модульный вход ММЕП. При этом на выходе ММЕП появляются данные S = 36999, которые и являются цифровой RSA-подписью для исходных данных М = 123456.
В качестве других частных случаев способа по второму варианту отмечается возможность реализации в виде многих иных комбинаций зависимых пунктов 13-22, а также возможность шифрования, дешифрования и перекодировки данных при их передаче от подателя к подписывающей стороне и наоборот, которые не меняют сущности заявленного изобретения. В частности, вид подписи, то есть набор используемых кратностей открытых RSA-экспонент может зависеть от времени изготовления подписывающей стороной подписи для замаскированных данных, а также может выражать степень доверия подписывающей стороны к подателю. Кроме того, правильность изготовленной цифровой RSA-подписи может быть проверена известными способами. Помимо этого, открытая RSA-экспонента, соответствующая использованному подписывающей стороной секретному ключу, может быть представлена набором данных, соответствующих ее множителям.
Указанный выше технический результат при реализации изобретения достигается тем, что способ изготовления вслепую цифровой RSA-подписи по третьему варианту, заключающийся в выборе тестированием секретных множителей и соответствующего им RSA- модуля, выборе открытой RSA-экспоненты и соответствующего секретного RSA-ключа, выборе исходных данных, выборе рандомизированного маскировочного ключа, выборе шифровального RSA- ключа, модуль которого соответствует выбранному RSA-модулю, а экспонента которого соответствует выбранному рандомизированному маскировочному ключу, которым осуществляют RSA-шифрование при создании замаскированных данных, для которых создают цифровую RSA- подпись, демаскировки созданной цифровой RSA-подписи для замаскированных данных, которую производят введением ее, рандомизированного маскировочного ключа, RSA-модуля и открытой RSA-экспоненты в демаскирующий преобразователь, выходные данные которого принимают в качестве цифровой RSA-подписи для выбранных исходных данных, отличается от известного способа изготовления вслепую неожидаемой цифровой подписи, выбранного в качестве прототипа, тем, что при создании замаскированных данных осуществляют RSA-шифрование выбранных исходных данных, при демаскировке созданной цифровой RSA-подписи для замаскированных данных дополнительно вводят в демаскирующий преобразователь выбранные исходные данные, при выборе секретных множителей осуществляют их дополнительное тестирование на несравнимость с единицей по модулю делителей в задаваемом диапазоне, на основе которого дополнительно выбирают маскирующий множитель, дополнительно создают на основе RSA-модуля множитель маскировочного ключа, рандомизированный маскировочный ключ выбирают взаимно простым относительно выбранной открытой RSA-экспоненты и кратным выбранному маскирующему множителю и созданному множителю маскировочного ключа, а RSA- модуль выбирают соответствующим двум секретным множителям.
Указанный выше технический результат в частных случаях конкретной реализации может достигаться, кроме того, тем, что при выборе секретных множителей в качестве критерия их отбора принимают несравнимость с единицей по модулю тех делителей из задаваемого диапазона, которые не являются делителями выбранного маскирующего множителя.
Более того, маскирующий множитель выбирают кратным тем делителям из задаваемого диапазона, по модулю которых сравним с единицей, по меньшей мере, один из выбранных секретных множителей,
Помимо этого, при выборе секретных множителей их отбор производят по наперед заданной вероятности отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных.
В частности, нижнюю границу задаваемого диапазона выбирают равной двум, а верхнюю границу задаваемого диапазона выбирают по наперед заданной вероятности отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных.
В частности, в качестве маскирующего множителя выбирают целое число, равное двум.
Помимо этого, выбор рандомизированного маскировочного ключа осуществляют посредством датчика случайных чисел. Более того, выбор рандомизированного маскировочного ключа производят тестированием четности выходных данных датчика случайных чисел и тестированием взаимной простоты выходных данных датчика случайных чисел относительно открытой RSA-экспоненты.
В частности, рандомизированный маскировочный ключ, выбранный кратным дополнительно созданному на основе RSA-модуля множителю маскировочного ключа, получают корректировкой выходных данных датчика случайных чисел множителем маскировочного ключа, а корректировку выходных данных датчика случайных чисел множителем маскировочного ключа при выборе рандомизированного маскировочного ключа осуществляют введением выходных данных датчика случайных чисел и множителя маскировочного ключа на вход умножителя, выходные данные которого принимают в качестве рандомизированного маскировочного ключа.
Более того, при демаскировке созданной цифровой RSA-подписи для замаскированных данных выбранные исходные данные, которые предварительно введены в демаскирующий преобразователь, подают на один из базовых входов содержащегося в нем модулярного мультипликативного евклидова преобразователя (ММЕП), на другой базовый вход которого подают созданную цифровую RSA-подпись для замаскированных данных, предварительно введенную в демаскирующий преобразователь, выбранный рандомизированный маскировочный ключ вводят на экспонентный вход ММЕП, соответствующий базовому входу, на который подают выбранные исходные данные, а открытую RSA- экспоненту вводят на экспонентный вход ММЕП, соответствующий базовому входу, на который подают созданную цифровую RSA-подпись для замаскированных данных.
Помимо этого, в качестве дополнительно создаваемого множителя маскировочного ключа выбирают наибольший делитель из взаимно простых относительно выбранной RSA-экспоненты делителей выбранного RSA-модуля, уменьшенного на единицу.
Сущность способа изготовления вслепую цифровой RSA-подписи по третьему варианту в основном, в том, что и указанная выше сущность заявляемого способа по первому варианту. Отличие состоит в том, что при реализации заявленного способа по третьему варианту подписывающая сторона при выборе секретных множителей P и Q может не беспокоится об отсутствии общих делителей P-1 и Q-1, больших двух, но составляет RSA-модуль N произведением в точности двух простых чисел. Кроме того, в качестве дополнительно создаваемого множителя маскировочного ключа податель выбирает тот наибольший делитель N - 1, который взаимно прост с открытой RSA-экспонентой. Данный способ изготовления цифровой RSA-подписи обеспечивает непрослеживаемость по тем же причинам, что и в способе изготовления цифровой RSA-подписи по первому варианту и, кроме того тем, что N-1 делится на все общие делители P-1 и Q-1. Это вытекает из того, что если N = P•Q, где P и Q - нечетные простые числа, а целое число D делит как число P - 1, так и число Q-1, то D является и делителем числа N-1, так как N-1=(Р-1)•Q+(Q-1).
Единая совокупность признаков третьего варианта заявленного способа, перечисленных выше, связана причинно-следственной связью с ранее изложенным техническим результатом изобретения, заключающимся в том, что при изготовлении вслепую неожидаемой цифровой RSA-подписи возможно использование неограниченного количества видов подписи; кроме того, не требуются растущие в зависимости от количества возможных видов подписи ресурсы, хранилища больших объемов данных и поиск в них, что, в свою очередь, приводит к ускорению и повышению надежности способа изготовления вслепую цифровой RSA-подписи.
Помимо этого, повышается достоверность непрослеживаемости за счет того, что свойства данных, обеспечивающих непрослеживаемость, могут быть, в некоторых из заявленных вариантов, протестированы непосредственно самим подателем. А именно, податель с помощью подписывающей стороны, но не доверяя ни ей, ни третьей стороне, может проверить, что RSA-модуль является произведением в точности двух секретных множителей P и Q и что маскирующий множитель кратен всем делителям P-1 и Q-1 в указанном диапазоне. При этом подписывающая сторона не доверяет своих секретов никакой третьей стороне.
Для тестирования того, что RSA-модуль N является произведением в точности двух простых множителей, подписывающая сторона сообщает заинтересованным сторонам пару чисел (U, V) такую, что каждый обратимый вычет по модулю N сравним с одним из чисел {l, U, V, UV}, будучи помноженным на квадратичный вычет по модулю N. После этого индивидуальный тестер может с помощью подписывающей стороны протестировать вышеуказанное свойство N, например, следующим способом. Тестер предоставляет случайное число X подписывающей стороне, которая возвращает тестеру данные Y такие, что Y2•X modN ∈ {1,U,V,UV}. Каждый такой ответ уменьшает вероятность того, что N состоит более чем из двух множителей, по меньшей мере в 2 раза. Для безопасности подписывающей стороны можно потребовать, чтобы X было либо простым числом, не превосходящим заданной границы, либо образом некоторой хэш-функции от указываемого тестером значения. Кроме того, если на такие запросы получены ответы для всех простых X меньше некоторой явной границы Т, то тестер может быть уверен, что N является произведением не более чем двух простых чисел. Предположим, что RSA-модуль N является произведением по меньшей мере трех простых чисел, а (U, V) произвольная пара вычетов по модулю N. Предположим, что для каждого простого нечетного L, меньшего Т, найдется такой вычет Y по модулю N, что вычет L•Y2 mod N принадлежит множеству (l, U, V, UV} . В этом случае, при выполнении расширенной гипотезы Римана, которая хотя и не доказана математически, но в значительной степени проверена экспериментально, величина T меньше, чем C[Log (N)]2, где значение C может быть получено с помощью известных оценок [8]. В частности, достаточно взять C = 70.
Для проверки того, что Р-1 и Q-1 не делятся на нечетное простое L, меньшее заданной границы, тестер предоставляет подписывающей стороне запрос R и получает ответ R1/L (mod N). Каждый такой ответ на запрос уменьшает в L раз вероятность того, что Р-1 или Q-1 делится на L. Для безопасности подписывающей стороны можно потребовать, чтобы R было либо меньше некоторой границы, либо образом некоторой хэш-функции от указываемого тестером значения. Кроме того, если на такие запросы получены ответы для всех простых R, меньших некоторой явной границы T, то тестер может быть уверен, что P-1 и Q-1 не имеют нечетных простых делителей L меньших заданной границы. Это следует из того, что если модуль N делится на нечетное простое число P, причем P - 1 делится на нечетное простое L, а для каждого вычета R по модулю N, где R меньше T, имеется вычет A такой, что AL ≡ R modN, то при выполнении расширенной гипотезы Римана, которая хотя и не доказана математически, но в значительной степени проверена экспериментально, величина T оценивается сверху величиной D(Log N)2, где значение D может быть получено с помощью известных оценок [8] . В частности, достаточно взять D = 70.
Вместо проверки того, что P-1 и Q-1 не делятся на L, для каждого индивидуального L достаточно проверить это свойство для такого набора чисел A1,. .., As, что каждое простое, меньшее заданной границы, является делителем хотя бы одного из Ai.
Ниже приведен пример конкретной реализации способа изготовления вслепую цифровой RSA-подписи по третьему варианту.
Пример 3
Подписывающая сторона создает секретные множители P и Q так же, как и в примере 1, за исключением того, что подписывающая сторона не обязана проверять условие (г) при выборе второго секретного множителя Q. Предположим, что выбраны секретные множители P = 659 и Q = 827. Заметим, что Н.О.Д.(Р-1, Q-1) = Н.О.Д.(658, 827) = 14 и тем самым условие (г) нарушено. После этого подписывающая сторона, как и в примере 1, создает RSA-модуль N = P•Q = 544993 и выбирает открытую RSA-экспоненту E, например E = 3, после чего RSA-модуль N и открытая RSA-экспонента E сообщаются всем заинтересованным потенциальным подателям.
Податель, желая изготовить вслепую цифровую RSA-подпись для исходных данных М = 123456 посредством датчика случайных чисел выбирает маскировочный ключ R, который взаимно прост с открытой RSA-экспонентой E = 3 и делится на наибольший делитель N-1 = 544993 взаимно простой с открытой RSA-экспонентой E = 3. Например, податель получает маскировочный ключ R посредством умножителя, на аргументные входы которого вводит выходные данные датчика случайных чисел, например, 901 и (N-1)/3 = 544992/3 = 181664, а на выходе которого появляется R = 901•181664 = 163679264. Далее, как в примере 1, податель создает замаскированные данные М' = МR (mod N) = 52602. Подписывающая сторона создает секретный ключ D = (N, D), как в примере 1, и получает D ≡ E-1(modϕ(N)) = 3-1(mod543508) = 362339. Далее подписывающая сторона, как в примере 1, создает цифровую RSA-подпись S' для замаскированных данных М' и получает S' = 447760. Получив цифровую RSA-подпись S' для замаскированных данных М, податель осуществляет их демаскировку, как в примере 1. При этом на выходе ММЕП появляются данные S = 405712, которые и являются цифровой RSA-подписью для исходных данных М = 123456.
В качестве других частных случаев способа по третьему варианту отмечается возможность реализации в виде многих иных комбинаций зависимых пунктов 24-35, а также возможность шифрования, дешифрования и перекодировки данных при их передаче от подателя к подписывающей стороне и наоборот, которые не меняют сущности заявленного изобретения. Разумеется, правильность изготовленной цифровой RSA-подписи может быть проверена известными способами.
В качестве исходных данных податель может выбрать имеющуюся у него цифровую RSA-подпись некоторых более ранних исходных данных и тем самым получить цифровую RSA-подпись более ранних исходных данных, соответствующую сумме открытой RSA-экспоненты, соответствующей уже имеющейся подписи и используемой открытой RSA-экспоненты.
После изготовления цифровой RSA-подписи для исходных данных, соответствующей открытой RSA-экспоненте E, податель может без помощи подписывающей стороны изготовить цифровую RSA-подпись для исходных данных, соответствующую произвольной открытой RSA-экспоненте, являющейся делителем E.
Указанный выше технический результат при реализации изобретения достигается тем, что способ изготовления вслепую цифровой RSA-подписи по четвертому варианту, заключающийся в выборе тестированием секретных множителей и соответствующего им RSA-модуля, выборе, по меньшей мере, одной открытой RSA-экспоненты, выборе исходных данных, выборе рандомизированного маскировочного ключа, выборе шифровального RSA-ключа, модуль которого соответствует выбранному RSA-модулю, а экспонента которого соответствует выбранному рандомизированному маскировочному ключу, которым осуществляют RSA-шифрование при создании замаскированных данных, произвольном выборе секретного RSA-ключа, соответствующего выбранным секретным множителям и открытым RSA-экспонентам, и создании соответствующей ему цифровой RSA-подписи для замаскированных данных, демаскировки созданной цифровой RSA-подписи для замаскированных данных, которую производят введением ее, рандомизированного маскировочного ключа, RSA-модуля и открытой RSA-экспоненты, соответствующей секретному RSA-ключу, использованному при создании цифровой RSA-подписи для замаскированных данных, в демаскирующий преобразователь, выходные данные которого принимают в качестве цифровой RSA-подписи для выбранных исходных данных, отличается от известного способа изготовления вслепую неожидаемой цифровой подписи, выбранного в качестве прототипа, тем, что при создании замаскированных данных осуществляют RSA-шифрование выбранных исходных данных, при демаскировке созданной цифровой RSA-подписи для замаскированных данных дополнительно вводят в демаскирующий преобразователь выбранные исходные данные, при выборе секретных множителей осуществляют их дополнительное тестирование на несравнимость с единицей по модулю делителей в задаваемом диапазоне, на основе которого дополнительно выбирают маскирующий множитель, дополнительно создают на основе RSA-модуля множитель маскировочного ключа, рандомизированный маскировочный ключ выбирают взаимно простым относительно выбранных открытых RSA-экспонент и кратным выбранному маскирующему множителю и созданному множителю маскировочного ключа, RSA-модуль выбирают соответствующим двум секретным множителям, а произвольный выбор секретного ключа осуществляют на основе произвольного выбора кратностей выбранных открытых RSA-экспонент.
Указанный выше технический результат в частных случаях конкретной реализации может достигаться, кроме того, тем, что при выборе секретных множителей в качестве критерия их отбора принимают несравнимость с единицей по модулю тех делителей из задаваемого диапазона, которые не являются делителями выбранного маскирующего множителя.
Более того, маскирующий множитель выбирают кратным тем делителям из задаваемого диапазона, по модулю которых сравним с единицей, по меньшей мере, один из выбранных секретных множителей.
Помимо этого, при выборе секретных множителей их отбор производят по наперед заданной вероятности отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных.
В частности, нижнюю границу задаваемого диапазона выбирают равной двум, а верхнюю границу задаваемого диапазона выбирают по наперед заданной вероятности отличия множества всех замаскированных данных, созданных по одним случайно выбранным исходным данным, от аналогичного множества для других случайно выбранных исходных данных.
В частности, в качестве маскирующего множителя выбирают целое число, равное двум.
Помимо этого, выбор рандомизированного маскировочного ключа осуществляют посредством датчика случайных чисел. Более того, выбор рандомизированного маскировочного ключа производят тестированием четности выходных данных датчика случайных чисел и тестированием взаимной простоты выходных данных датчика случайных чисел относительно выбранных открытых RSA-экспонент.
В частности, рандомизированный маскировочный ключ, выбранный кратным дополнительно созданному на основе RSA-модуля множителю маскировочного ключа, получают корректировкой выходных данных датчика случайных чисел множителем маскировочного ключа, а корректировку выходных данных датчика случайных чисел множителем маскировочного ключа при выборе рандомизированного маскировочного ключа осуществляют введением выходных данных датчика случайных чисел и множителя маскировочного ключа на вход умножителя, выходные данные которого принимают в качестве рандомизированного маскировочного ключа.
Более того, при демаскировке созданной цифровой RSA-подписи для замаскированных данных выбранные исходные данные, которые предварительно введены в демаскирующий преобразователь, подают на один из базовых входов содержащегося в нем модулярного мультипликативного евклидова преобразователя (ММЕП), на другой базовый вход которого подают созданную цифровую RSA-подпись для замаскированных данных, предварительно введенную в демаскирующий преобразователь, выбранный рандомизированный маскировочный ключ вводят на экспонентный вход ММЕП, соответствующий базовому входу, на который подают выбранные исходные данные, а открытую RSA- экспоненту вводят на экспонентный вход ММЕП, соответствующий базовому входу, на который подают созданную цифровую RSA-подпись для замаскированных данных.
Помимо этого, в качестве дополнительно создаваемого множителя маскировочного ключа выбирают наибольший делитель из взаимно простых относительно выбранных RSA-экспонент делителей выбранного RSA-модуля, уменьшенного на единицу.
Сущность способа изготовления вслепую цифровой RSA-подписи по четвертому варианту состоит, в основном, в том, что и указанная выше сущность заявляемого способа по третьему варианту. Отличие состоит в том, что при реализации заявленного способа по второму варианту подписывающая сторона выбирает несколько открытых RSA- экспонент E1,...Ek. Данный способ изготовления цифровой RSA-подписи обеспечивает непрослеживаемость по тем же причинам, что и в способе изготовления цифровой RSA-подписи по третьему варианту.
Единая совокупность признаков четвертого варианта заявленного способа, перечисленных выше, связана причинно-следственной связью с ранее изложенным техническим результатом изобретения, заключающимся в том, что при изготовлении вслепую неожидаемой цифровой RSA-подписи возможно использование неограниченного количества видов подписи; кроме того, не требуются растущие в зависимости от количества возможных видов подписи ресурсы, хранилища больших объемов данных и поиск в них, что, в свою очередь, приводит к ускорению и повышению надежности способа изготовления вслепую цифровой RSA-подписи.
Помимо этого, как и в заявленном способе по третьему варианту, повышается достоверность непрослеживаемости за счет того, что свойства данных, обеспечивающих непрослеживаемость, могут быть, в некоторых из заявленных вариантов, протестированы непосредственно самим подателем. А именно, податель с помощью подписывающей стороны, но не доверяя ни ей, ни третьей стороне, может проверить, что RSA-модуль является произведением в точности двух секретных множителей P и Q и что маскирующий множитель кратен всем делителям Р-1 и Q-1 в указанном диапазоне. При этом подписывающая сторона не доверяет своих секретов никакой третьей стороне.
Ниже приведен пример конкретной реализации способа изготовления вслепую цифровой RSA-подписи по четвертому варианту.
Пример 4
Подписывающая сторона выбирает секретные множители P и Q и создает RSA-модуль N так же, как и в примере 3, а открытые RSA-экспоненты, как в примере 2. Предположим, что созданы секретные множители P = 659 и Q = 827, RSA-модуль N = 544993, открытые RSA-экспоненты E1 = 3 и E2 = 5. Как и в примере 5 RSA-модуль N и открытые RSA-экспоненты сообщаются всем заинтересованным потенциальным подателям.
Предположим, что податель, желая изготовить вслепую цифровую RSA-подпись для исходных данных М = 123456, выбрал маскировочный ключ R = 163679264 и создал замаскированные данные М'=(123456)163679264 (mod 544993) = 52602.
Подписывающая сторона, как в примере 2, выбирает кратности созданных открытых RSA-экспонент, например r1 = 6 и r2 = 4, и создает секретный ключ (N, D), где D = 314269. Далее подписывающая сторона создает цифровую RSA-подпись S' для замаскированных данных М', как в примере 2, и получает S' = (М')D (mod N) = 539387. Получив цифровую RSA-подпись S' для замаскированных данных М', податель осуществляет демаскировку данных S' так же, как в примере 2. При этом на выходе ММЕП появляются данные S = 404253, которые и являются цифровой RSA-подписью для исходных данных М = 123456.
В качестве других частных случаев способа по четвертому варианту отмечается возможность реализации в виде многих иных комбинаций зависимых пунктов 37-48, а также возможность шифрования, дешифрования и перекодировки данных при их передаче от подателя к подписывающей стороне и наоборот, которые не меняют сущности заявленного изобретения. В частности, вид подписи, то есть набор используемых кратностей открытых RSA-экспонент может зависеть от времени изготовления подписывающей стороной подписи для замаскированных данных, а также может выражать степень доверия подписывающей стороны к подателю. Кроме того, правильность изготовленной цифровой RSA-подписи может быть проверена известными способами. Помимо этого, открытая RSA-экспонента, соответствующая использованному подписывающей стороной секретному ключу, может быть представлена набором данных, соответствующих ее множителям.
Указанный выше технический результат при реализации изобретения достигается тем, что способ изготовления вслепую цифровой RSA-подписи по пятому варианту, заключающийся в выборе секретных множителей и соответствующего им RSA-модуля, выборе, по меньшей мере, одной открытой RSA-экспоненты, выборе исходных данных, выборе рандомизированного маскировочного ключа, выборе, по меньшей мере одного, шифровального RSA-ключа, модуль которого соответствует выбранному RSA-модулю, и которым при создании замаскированных данных осуществляют RSA-шифрование выбранного рандомизированного маскировочного ключа, причем результатом RSA-шифрования при создании замаскированных данных обрабатывают выбранные исходные данные, произвольном выборе секретного RSA-ключа, соответствующего выбранным секретным множителям и выбранным открытым RSA-экспонентам, и создании соответствующей ему цифровой RSA-подписи для замаскированных данных, создание демаскировочного ключа путем обработки маскировочного ключа открытой RSA-экспонентой, соответствующей использованному при создании цифровой RSA-подписи для замаскированных данных секретному RSA-ключу, демаскировки созданной цифровой RSA-подписи для замаскированных данных, которую производят введением ее, демаскировочного ключа и RSA-модуля в демаскирующий преобразователь, выходные данные которого принимают в качестве цифровой RSA-подписи для выбранных исходных данных, отличается от известного способа изготовления вслепую неожидаемой цифровой подписи, выбранного в качестве прототипа, тем, что перед созданием замаскированных данных дополнительно выбирают произвольные ограничительные кратности открытых RSA-экспонент, RSA-шифрование выбранного рандомизированного маскировочного ключа производят RSA-ключом, в качестве модуля которого берут выбранный RSA-модуль, а RSA-экспонента которого соответствует произведению выбранных открытых RSA-экспонент, соответственно выбранной ограничительной кратности каждой из них, перед произвольным выбором секретного RSA-ключа на основе открытых RSA-экспонент осуществляют произвольный выбор используемых кратностей открытых RSA-экспонент в диапазоне произвольно выбранных перед созданием замаскированных данных ограничительных кратностей открытых RSA- экспонент, а демаскировочный ключ создают посредством последовательных RSA-шифрований маскировочного ключа шифровальными RSA-ключами, в качестве модуля которых берут RSA-модуль, а в качестве RSA-экспонент которых берут открытые RSA-экспоненты, причем каждую из них берут в кратности, равной разности выбранной перед созданием замаскированных данных, соответствующей ей ограничительной кратности, и выбранной перед произвольным выбором секретного ключа, соответствующей ей используемой кратности.
Указанный выше технический результат в частных случаях конкретной реализации может достигаться, кроме того, тем, что выбор рандомизированного маскировочного ключа осуществляют посредством датчика случайных чисел.
Сущность способа изготовления вслепую цифровой RSA-подписи по пятому варианту состоит в том, что подписывающая сторона выбирает секретные множители, соответствующий им RSA-модуль N и набор открытых RSA-экспонент E1,..., Ek так же, как и в прототипе. Открытые RSA-экспоненты E1,..., Ek могут быть названы базовыми экспонентами, поскольку RSA-экспонента того открытого RSA-ключа, которому будет соответствовать изготавливаемая цифровая RSA-подпись, может соответствовать произведению RSA-экспонент E1,...,Ek, взятых с произвольными кратностями, где под кратностью открытой RSA-экспоненты имеется в виду произвольное неотрицательное целое число. RSA-модуль N и открытые RSA-экспоненты E1,..., Ek сообщаются всем заинтересованным потенциальным подателям. Податель, желая изготовить вслепую цифровую RSA-подпись для исходных данных М, выбирает в качестве рандомизированного маскировочного ключа целое число r и произвольные ограничительные кратности u1,..., uk открытых RSA-экспонент. На практике этот выбор может определяться внешними обстоятельствами, но мотивы этого выбора не существенны для настоящего изобретения. Рандомизация достигается тем, что r выбирается посредством датчика случайных чисел. Далее податель создает замаскированные данные М' в соответствии с формулой М' = M•R (mod N), где R получают посредством RSA-шифрования маскировочного ключа r RSA-ключом, в качестве модуля которого берут выбранный RSA-модуль N, а RSA-экспонента которого соответствует произведению выбранных открытых RSA-экспонент, соответственно выбранной ограничительной кратности каждой из них. Иными словами, RSA-шифрования маскировочного ключа r осуществляют в соответствии с формулой R = rU (mod N), где U = U1...Uk, а U1 = E1 u1, . ., Uk = Ek uk. Подписывающая сторона выбирает произвольные используемые кратности созданных открытых RSA-экспонент r1,..., rk в пределах выбранных ограничительных кратностей u1,...,uk. На практике этот выбор может определяться внешними обстоятельствами, но мотивы этого выбора не существенны для настоящего изобретения. Далее подписывающая сторона выбирает секретный RSA-ключ, соответствующий выбранным секретным множителям, выбранным открытым RSA-экспонентам и выбранным используемым кратностям. Иными словами, подписывающая сторона выбирает секретный RSA-ключ, представляющий собой пару (N, D), где D = D1 u1...Dk uk, a Dj - секретная RSA-экспонента, соответствующая открытой RSA-экспоненте Ej. Подписывающая сторона создает цифровую RSA-подпись S' для замаскированных данных М' так же, как в прототипе, то есть в соответствии с формулой S' = (М')D (mod N). Податель, по выбранным подписывающей стороной используемым кратностям открытых RSA-экспонент r1, . . . , rk, создает демаскировочный ключ T в соответствии с формулой T = rv1...vk(mod N), где V1 = E1 u1...vk,..., Vk = Ek uk-rk. Получив цифровую RSA-подпись S' для замаскированных данных М', податель осуществляет демаскировку S' посредством модулярного инвертора и модулярного умножителя в соответствии с формулой S = S'•T-1 (mod N).
Единая совокупность признаков заявленного способа по пятому варианту, перечисленных выше, связана причинно-следственной связью с ранее изложенным техническим результатом изобретения, заключающимся в том, что при изготовлении вслепую неожидаемой цифровой RSA-подписи возможно использование неограниченного количества видов подписи; кроме того, не требуются растущие в зависимости от количества возможных видов подписи ресурсы, хранилища больших объемов данных и поиск в них, что, в свою очередь, приводит к ускорению и повышению надежности способа изготовления вслепую цифровой RSA-подписи.
Ниже приведен пример конкретной реализации способа изготовления вслепую цифровой RSA-подписи по пятому варианту.
Пример 5
Предположим, что подписывающая сторона выбрала в качестве секретных множителей P, Q и RSA-модуля N, и открытых RSA-экспонент следующие данные: P = 29, Q = 59, N = P•Q = 29•59 = 1711, E1 = 3 и E2 = 5. Как в примере 4 RSA-модуль 1711 и открытые RSA-экспоненты 3 и 5 сообщаются всем заинтересованным потенциальным подателям.
Предположим, что податель желает изготовить вслепую цифровую RSA-подпись исходных данных М = 1234, причем маскировочный ключ r, выбранный посредством датчика случайных чисел, равен 901, а в качестве ограничительных кратностей открытых RSA-экспонент выбраны u1 = 10, a u2 = 8. Далее податель посредством модулярного умножителя и модулярного экспоненциатора в соответствии с формулой R = гU (mod N), где U1 = E1 u1 = 310 = 59049, U2=E2 u2=58=390625, U = U1•U2, получает целое число R = 164 и создает посредством модулярного умножителя замаскированные данные М' в соответствии с формулой М' = М•R (mod N) = 478.
Подписывающая сторона выбирает произвольные используемые кратности созданных открытых RSA-экспонент r1 и r2 в пределах выбранных ограничительных кратностей u1 = 10 и r2 = 8. Предположим, что r1 = 7 и r2 = 6. Далее подписывающая сторона создает секретный ключ D = (N, D), как в примере 2, и получает D = 1307. Далее подписывающая сторона, как и в примере 1, создает цифровую RSA-подпись S' для замаскированных данных М' и получает S'= (М')D (mod N) = 967.
Податель, узнав выбранные подписывающей стороной используемые кратности открытых RSA-экспонент r1 = 7 и r2 = 6, создает демаскировочный ключ T в соответствии с формулой T = rv1xv2 (mod N), где V1 = E1 u1-r1 = 27, а V2 = E2 u2-r2 = 25, и получает T = 936. Получив цифровую RSA-подпись S' для замаскированных данных М', податель осуществляет демаскировку данных S' в соответствии с формулой S = S'•T-1 (mod N) и получает цифровую RSA-подпись S = 1096 для исходных данных М = 1234.
В качестве других частных случаев способа по пятому варианту отмечается возможность шифрования, дешифрования и перекодировки данных при их передаче от подателя к подписывающей стороне и наоборот, которые не меняют сущности заявленного изобретения. В частности, вид подписи, то есть набор используемых кратностей открытых RSA-экспонент, может зависеть от времени изготовления подписывающей стороной подписи для замаскированных данных, а также может выражать степень доверия подписывающей стороны к подателю. Кроме того, правильность изготовленной цифровой RSA-подписи может быть проверена известными способами.
Предложенные варианты заявленного способа изготовления цифровой RSA-подписи реализуются вариантами заявленного устройства.
Предложено несколько вариантов устройства для изготовления вслепую цифровой RSA-подписи.
Устройство для изготовления вслепую цифровой RSA-подписи по первому варианту, содержащее блок выбора маскировочного ключа с датчиком случайных чисел, блок маскировки с модулярным экспоненциатором, модульный вход которого соединен с модульным входом блока маскировки, а экспонентный вход которого соединен со входом маскировочного ключа блока маскировки, блок маскировки имеет вход исходных данных и один выход, который соединен со входом данных подписи блока подписи, который имеет вход секретного ключа и один выход, который соединен с входом данных демаскировки блока демаскировки, который имеет выход подписи, модульный вход, экспонентный вход и вход маскировочного ключа, к которому подсоединен выход блока маскировочного ключа, отличается от известного устройства для изготовления вслепую неожидаемой цифровой подписи, выбранного в качестве прототипа, тем, что базовый вход модулярного экспоненциатора блока маскировки соединен с входом исходных данных блока маскировки, а его выход соединен с выходом блока маскировки, блок демаскировки дополнительно имеет вход исходных данных и содержит модулярный мультипликативный евклидов преобразователь (ММЕП) с модульным входом, базовыми входами и соответствующими каждому из них экспонентными входами, причем модульный вход блока демаскировки соединен с модульным входом ММЕП, вход исходных данных блока демаскировки соединен с одним из базовых входов ММЕП, а вход данных демаскировки блока демаскировки соединен с другим базовым входом ММЕП, вход маскировочного ключа блока демаскировки соединен с экспонентным входом ММЕП, который соответствует базовому входу ММЕП, соединенному с входом данных демаскировки блока демаскировки, а экспонентный вход блока демаскировки соединен с экспонентным входом ММЕП, который соответствует базовому входу ММЕП, соединенному с входом исходных данных блока демаскировки, а выход блока демаскировки соединен с выходом ММЕП, блок выбора маскировочного ключа дополнительно содержит арифметический контроллер с двумя ограничительными входами, которые условно приняты за первый и второй ограничительные входы, причем арифметический контроллер соединен с датчиком случайных чисел, выход арифметического контроллера соединен с выходом блока выбора маскировочного ключа, а арифметический контроллер выполнен таким, что обеспечивает взаимную простоту выходных данных блока выбора маскировочного ключа относительно целых чисел, поданных на первый ограничительный вход арифметического контроллера, и делимость выходных данных блока выбора маскировочного ключа на целое число, поданное на второй его ограничительный вход.
Указанный выше технический результат в частных случаях конкретной реализации заявленного устройства по первому варианту может достигаться, кроме того, тем, что соединение арифметического контроллера с датчиком случайных чисел выполнено путем соединения выхода датчика случайных чисел со входом, условно принятым за вход пробных данных арифметического контроллера, а взаимная простота выхода блока выбора маскировочного ключа относительно целых чисел, поданных на первый ограничительный вход арифметического контроллера, и делимость выхода блока выбора маскировочного ключа на целое число, поданное на второй его ограничительный вход, обеспечена тем, что арифметический контроллер содержит умножитель и тестер взаимной простоты, причем первый ограничительный вход арифметического контроллера соединен со входом тестера взаимной простоты, вход пробных данных соединен с другим входом тестера взаимной простоты и с аргументным входом умножителя, выход тестера взаимной простоты соединен со входом загрузки умножителя, второй ограничительный вход арифметического контроллера соединен с аргументным входом умножителя, выход которого соединен с выходом арифметического контроллера.
Сущность устройства для изготовления вслепую цифровой RSA-подписи по первому варианту состоит в том, что с его помощью податель, при участии подписывающей стороны, может изготовить вслепую цифровую RSA-подпись для исходных данных по первому и второму вариантам заявленного способа. Кроме того, с помощью такого устройства податель, при участии подписывающей стороны, может изготовить вслепую цифровую RSA-подпись для исходных данных по третьему и четвертому вариантам заявленного способа в том случае, если открытые RSA-экспоненты взаимно просты с уменьшенным на единицу RSA-модулем.
Для этого податель вводит исходные данные М на вход исходных данных, а известный из сообщения подписывающей стороны RSA-модуль N на модульный вход блока маскировки. Кроме того, податель вводит открытую RSA-экспоненту на первый ограничительный вход арифметического контроллера. Далее податель вводит на второй ограничительный вход арифметического контроллера маскирующий множитель, а при использовании заявленного устройства для реализации способов, заявленных по третьему и по четвертому вариантам, податель дополнительно вводит на второй ограничительный вход арифметического контроллера уменьшенный на единицу RSA-модуль. Маскировочный ключ R появляется на выходе блока выбора маскировочного ключа и поступает на вход маскировочного ключа блока маскировки, на выходе которого появляются замаскированные данные М'. Подписывающая сторона вводит на вход секретного ключа блока подписи секретный ключ (N, D), соответствующий выбранной открытой RSA-экспоненте E. На вход данных подписи блока подписи поступают замаскированные данные М', а на выходе блока подписи появляется цифровая RSA-подпись Т' для замаскированных данных М', которая поступает на вход данных демаскировки блока демаскировки. Кроме того, податель вводит на модульный вход, вход исходных данных и экспонентный вход блока демаскировки, соответственно, RSA-модуль N, исходные данные М и открытую RSA- экспоненту E. Помимо этого, на вход маскировочного ключа блока демаскировки поступает маскировочный ключ R с выхода блока выбора маскировочного ключа. На выходе блока демаскировки появляется цифровая RSA-подпись S для исходных данных М.
При этом соединения между различными блоками могут быть выполнены посредством телекоммуникационных сетей, а сами блоки могут быть удалены друг от друга.
Единая совокупность признаков заявленного устройства по первому варианту, перечисленных выше, связана причинно- следственной связью с ранее изложенным техническим результатом изобретения, заключающимся в том, что при изготовлении вслепую неожидаемой цифровой RSA-подписи возможно использование неограниченного количества видов подписи; кроме того, не требуются растущие в зависимости от количества возможных видов подписи ресурсы, хранилища больших объемов данных и поиск в них, что, в свою очередь, приводит к ускорению и повышению надежности способа изготовления вслепую цифровой RSA-подписи.
Ниже приведен пример конкретной реализации устройства для изготовления вслепую цифровой RSA-подписи по первому варианту.
Пример 6
Пример проиллюстрирован фиг. 1, на которой изображено устройство, содержащее блок выбора маскировочного ключа 1, блок маскировки 2, блок подписи 3 и блок демаскировки 4. Блок выбора маскировочного ключа содержит датчик случайных чисел 5 и арифметический контроллер 6, имеющий вход недопустимых делителей 7, вход обязательных делителей 8 и вход пробных данных 9, причем выход датчика случайных чисел соединен со входом пробных данных 9 арифметического контроллера, а выход арифметического контроллера 6 соединен с выходом блока создания маскировочного ключа. Блок маскировки 2 имеет вход исходных данных 10, модульный вход 11, вход маскировочного ключа 12 и содержит не показанный на фиг.1 модулярный экспоненциатор, причем вход исходных данных 10, вход маскировочного ключа 12 и модульный вход 11 блока маскировки соединены соответственно с базовым входом, экспонентным входом и модульным входом модулярного экспоненциатора. Блок подписи 3 имеет вход секретного ключа 13 и вход данных подписи 14, причем вход данных подписи 14 блока подписи 3 соединен с выходом блока маскировки 2. Блок демаскировки 4 имеет вход данных демаскировки 15, модульный вход 16, экспонентный вход 17, вход маскировочного ключа 18 и вход исходных данных 19 и содержит не показанный на фиг. 1 модулярный мультипликативный евклидов преобразователь (ММЕП), причем модульный вход 16 соединен с модульным входом ММЕП, вход исходных данных 19 соединен с одним из базовых входов ММЕП, а вход данных демаскировки 15 соединен с другим базовым входом ММЕП, вход маскировочного ключа 18 соединен с экспонентным входом ММЕП, соответствующим базовому входу ММЕП, соединенному с входом данных демаскировки 15, а экспонентный вход 17 соединен с экспонентным входом ММЕП, соответствующим базовому входу ММЕП, соединенному с входом исходных данных 19, а выход ММЕП соединен с выходом блока демаскировки.
Конкретный пример работы вышеописанного устройства для изготовления вслепую цифровой RSA-подписи по первому варианту состоит в следующем. Предположим, что подписывающая сторона выбрала секретные множители P=419 и Q= 863, RSA-модуль N=361597, открытую RSA-экспоненту E = 3, после чего сообщила RSA-модуль N, открытую RSA-экспоненту E всем заинтересованным сторонам. Предположим, что податель желает изготовить вслепую цифровую RSA- подпись исходных данных М = 123456. Для этого податель вводит исходные данные М = 123456 на вход исходных данных 10, а RSA- модуль N = 361597 на модульный вход 11 блока маскировки 2. Кроме того, податель вводит открытую RSA-экспоненту E = 3 на первый ограничительный вход 7 арифметического контроллера 6, а уменьшенный на единицу RSA-модуль N, то есть целое число 123455, на второй ограничительный вход 8 арифметического контроллера 6. Предположим, что на выходе блока выбора маскировочного ключа 111 появилось целое число R= 901. Целое число R = 901 поступает на вход маскировочного ключа 12 блока маскировки 2, на выходе которого появляются данные М' = 237367. Подписывающая сторона вводит на вход секретного ключа 13 блока подписи 3 секретный ключ (N, D), соответствующий открытой RSA-экспоненте, то есть D = 240211. На вход данных подписи 14 блока подписи 3 поступает целое число М' = 237367, а на выходе блока подписи 3 появляется целое число Т' = 88275, которое поступает на вход данных демаскировки 15 блока демаскировки 4. Кроме того, податель вводит на модульный вход 16, вход исходных данных 19 и экспонентный вход 17 блока демаскировки 4, соответственно, RSA-модуль N = 361597, исходные данные М = 123456 и открытую RSA-экспоненту экспоненту E = 3. Помимо этого, на вход маскировочного ключа 18 блока демаскировки 4 поступает целое число R = 901. На выходе блока демаскировки появляются данные Т = 150340, которые и являются цифровой RSA-подписью для исходных данных М = 123456.
В качестве других частных случаев устройства по первому варианту отмечается возможность его реализации в виде многих иных разбиений содержащихся в нем вспомогательных устройств на блоки, которые не меняют сущности заявленного изобретения. Также возможно выполнять соединения между блоками путем пропускания этих соединений через дополнительные устройства. Среди таких дополнительных устройств могут быть, в частности, шифровальные и дешифровальные устройства, а также кодирующие и декодирующие устройства. Кроме того, заявленное устройство может быть дополнено другими известными устройствами, в частности, устройствами для проверки RSA-подписи.
Кроме того, в приведенном ниже примере 7 описан частный случай реализации арифметического контроллера, содержащегося в блоке выбора маскировочного ключа заявленного устройства для изготовления вслепую цифровой RSA-подписи по первому варианту и приводится конкретный пример работы указанного блока выбора маскировочного ключа.
Пример 7
Пример проиллюстрирован фиг.2 и вышеуказанной фиг. 1. На Фиг.2 изображен арифметический контроллер 6, который имеет вход недопустимых делителей 7, вход обязательных делителей 8, вход пробных данных 9, содержит умножитель 20 и тестер взаимной простоты 21. При этом вход недопустимых делителей 7 соединен со входом 22 тестера взаимной простоты, вход пробных данных 9 соединен со входом 23 тестера взаимной простоты и с аргументным входом 24 умножителя 20, выход тестера взаимной простоты 21 соединен со входом загрузки 25 умножителя 20, вход обязательных делителей 8 арифметического контроллера 6 соединен с аргументным входом 26 умножителя 20, выход которого соединен с выходом арифметического контроллера 6.
Конкретный пример работы блока выбора маскировочного ключа 1 вышеописанного устройства для изготовления вслепую цифровой RSA-подписи по первому варианту состоит в следующем. Предположим, что на выходе датчика случайных чисел 5 появляется целое число 1234, которое попадает на вход пробных данных 9 арифметического контроллера 6. Предположим, что на первый ограничительный вход 7 подано целое число 7, а на второй ограничительный вход 8 подано целое число 5. Целые числа 1234 и 7 поступают, соответственно, на входы 23 и 22 тестера взаимной простоты 21, на выходе которого появляется логическое значение 1 ("истина"). Это значение поступает на вход загрузки 25 умножителя 20, после чего умножитель 20 вбирает данные 1234 и 5, поданные соответственно на его аргументные входы 24 и 26. На выходе умножителя 20 появляется целое число 1234•5= 6170, которое и появляется на выходе арифметического контроллера 6 и на выходе блока выбора маскировочного ключа 1.
Пример 8
Как указано выше в тексте описания (перед описанием сущности способа изготовления вслепую цифровой RSA-подписи по первому варианту), в примере 8 приведен частный случай реализации ММЕП и его работы. Пример проиллюстрирован фиг. 3, на которой изображен ММЕП 27 с модульным входом 28, базовым входом 29 и соответствующим ему экспонентным входом 30, базовым входом 31 и соответствующим ему экспонентным входом 32. Кроме того ММЕП 27 содержит обобщенный евклидов преобразователь (ОЕП) 33, модулярные экспоненциаторы 34 и 35 и модулярный умножитель 36. При этом модульный вход 28 соединен с модульными входами модулярных экспоненциаторов 34 и 35 и модулярного умножителя 36, но эти модульные входы и соединения не показаны на фиг.3. Кроме того базовый вход 29 соединен с базовым входом модулярного экспоненциатора 34, базовый вход 31 соединен с базовым входом модулярного экспоненциатора 35, экспонентный вход 30 соединен с первым входом 37 ОЕП 33, экспонентный вход 32 соединен со вторым входом 38 ОЕП 33, первый выход 39 ОЕП 33 соединен с экспонентным входом модулярного экспоненциатора 34, второй выход 40 ОЕП 33 соединен с экспонентным входом модулярного экспоненциатора 35, выходы модулярных экспоненциаторов 34 и 35 соединены с аргументными входами модулярного умножителя 36, выход которого соединен с выходом ММЕП.
Под обобщенным евклидовым преобразователем (ОЕП) имеется в виду устройство, имеющее модульный вход, два аргументных входа, условно принятые за первый и второй входы, и два соответствующих выхода, условно принятые за первый и второй выходы, причем если на первый вход подано целое число A, на второй вход подано целое число В, причем целые числа A и B взаимно просты, то на первом выходе появляется целое число C, а на втором выходе появляется целое число D, такие, что A•C+B•D=1. В литературе ([7], стр. 367-368) имеются сведения, достаточные для создания ОЕП специалистами среднего уровня, а для подтверждения реализуемости ОЕП ниже в примере 9 приведен пример конкретной реализации ОЕП.
Конкретный пример работы ММЕП 27 состоит в следующем. Предположим, что на модульный вход 28, базовый вход 29, базовый вход 31, экспонентный вход 30 и экспонентный вход 32 ММЕП 27 соответственно поступили данные N = 37, X = 5, Y = 8, A = 17 и B= 11. Данные A = 17 и B = 11 поступают после этого соответственно на первый аргументный вход 37 и на второй аргументный вход 38 ОЕП 33, на первом выходе 39 которого появляются данные С = 2, а на втором выходе 40 которого появляются данные D = -3. На модульный вход, экспонентный вход и базовый вход модулярного экспоненциатора 34 поступают соответственно данные N = 37, С =2 и X= 5, а его на выходе появляются данные G = 52 (mod 37) = 25. На модульный вход, экспонентный вход и базовый вход модулярного экспоненциатора 35 поступают соответственно данные N = 37, D = -3 и Y = 8, а на его выходе появляются данные H = 8-3 (mod 37) = 31. На модульный вход и два аргументных входа модулярного умножителя 36 поступают соответственно данные N = 37, G = 25 и H = 31, а на его выходе появляются данные Z = 25•31 (mod 37) = 35, которые и появляются на выходе ММЕП 27.
Пример 9
Для подтверждения реализуемости частного случая ММЕП, приведенного в примере 8, описан конкретный пример ОЕП, проиллюстрированный фиг.4. На фиг.4 изображен ОЕП 33, который имеет первый вход 37, второй вход 38, первый выход 39 и второй выход 40. ОЕП содержит регистры 41- 52, умножители 53-55, вычитатели 56 - 58, вычислитель частного 59, компаратор 60 и элемент "НЕ" 61. При этом первый вход 37 соединен с входом данных регистра 41, а второй вход 38 соединен со входом данных регистра 42. Кроме того ОЕП 33 содержит не показанные на фиг.4 регистр первого выхода и регистр второго выхода, причем выход регистра первого выхода соединен с первым выходом 39, а выход регистра второго выхода соединен со вторым выходом 40, вход данных регистра первого выхода соединен с выходом регистра 49, а вход данных регистра второго выхода соединен с выходом регистра 50. Выход регистра 41 соединен с входом делимого 62 вычислителя частного 59 и со входом уменьшаемого 63 вычитателя 56. Выход регистра 42 соединен со входом делителя 64 вычислителя частного 59, со входом 65 умножителя 53 и со входом данных регистра 47. Выход регистра 43 соединен со входом уменьшаемого 66 вычитателя 57. Выход регистра 44 соединен со входом 67 умножителя 54 и со входом данных регистра 49. Выход регистра 45 соединен со входом уменьшаемого 68 вычитателя 58. Выход регистра 46 соединен со входом 69 умножителя 55 и со входом данных регистра 51. Выход вычислителя частного 59 соединен со входом 70 умножителя 53, со входом 71 умножителя 54 и со входом 72 умножителя 55. Выход умножителя 53 соединен со входом вычитаемого 73 вычитателя 56, выход умножителя 54 соединен со входом вычитаемого 74 вычитателя 57, а выход умножителя 55 соединен со входом вычитаемого 75 вычитателя 58. Выход вычитателя 56 соединен со входом данных регистра 48, выход вычитателя 57 соединен со входом данных регистра 50, а выход вычитателя 58 соединен со входом данных регистра 52. Выход регистра 47 соединен со входом данных регистра 41, выход регистра 48 соединен со входом данных регистра 42, выход регистра 49 соединен со входом данных регистра 43, выход регистра 50 соединен со входом данных регистра 44, выход регистра 51 соединен со входом данных регистра 45, выход регистра 52 соединен со входом данных регистра 46, но эти соединения не показаны. Выход регистра 48 соединен со входом 76 компаратора 60, а выход компаратора 60 соединен со входом загрузки регистров первого и второго выходов и со входом логического элемента "НЕ" 61, выход которого соединен со входами загрузки регистров 41-46, но эти соединения не показаны. Кроме того, ОЕП 33 включает схему начальной установки регистров 41-46, схему подачи нуля на вход 77 компаратора 60 и схему синхронизации, обеспечивающую пошаговый режим работы ОЕП 33, но эти схемы не показаны.
Конкретный пример работы ОЕП 33 состоит в следующем. Предположим, что на первый вход 37 и второй вход 38 ОЕП 33 поданы соответственно данные A = 7 и B = 5. После этого схема начальной установки загружает в регистры 41, 42, 43, 44, 45 и 46 соответственно значения R1 = A = 7 со входа 37, R2 = В = 5 со входа 38, U1 = 1, U2 = 0, V1 = 0 и V2 = 1. Работа ОЕП 33 проходит пошагово, что обеспечивается схемой синхронизации.
Опишем в деталях работу ОЕП 33 на первом шаге. На вход делимого 62 и на вход делителя 64 вычислителя частного 59 поступают соответственно данные R1 = 7 из регистра 41 и данные R2 = 5 из регистра 42, а на его выходе появляется неполное частное Q = 1 от деления R1 = 7 на R2 = 5. Данные Q = 1 появляются на входе 70 умножителя 53, на входе 71 умножителя 54 и на входе 72 умножителя 55. На вход 67 умножителя 54 поступают данные R2 = 5 из регистра 42, а на его выходе появляются данные Q•R2 = 5, которые попадают на вход вычитаемого 73 вычитателя 56. На вход уменьшаемого 63 вычитателя 56 поступают данные R1 = 7 из регистра 41, а на выходе вычитателя 56 появляются данные R1 - Q•R2 = 2, которые поступают в регистр 48. В регистр 47 поступают данные R2 = 5 из регистра 42. На вход 67 умножителя 54 поступают данные U2 = О из регистра 44, а на его выходе появляются данные Q•U2 = 0, которые и попадают на вход вычитаемого 74 вычитателя 57. На вход уменьшаемого 66 вычитателя 57 поступают данные U1 = 1 из регистра 43, а на выходе вычитателя 57 появляются данные U1 - Q•U2 = 1, которые поступают в регистр 50. В регистр 49 поступают данные U2 = 0 из регистра 44. На вход 69 умножителя 55 поступают данные V2 = 1 из регистра 46, а на его выходе появляются данные Q•V2 = 1, которые поступают на вход вычитаемого 75 вычитателя 58. На вход уменьшаемого 68 вычитателя 58 поступают данные V1 = 0 из регистра 45, а на выходе вычитателя 58 появляются данные V1 - Q•V2 = -1, которые поступают в регистр 52. В регистр 51 поступают данные V2 = 1 из регистра 46. На вход 76 компаратора 60 из регистра 48 поступают данные N = 2, на вход 77 компаратора 60 схемой подачи нуля подается ноль, а на выходе компаратора 60 появляется логическое значение 0 ("ложь"), которое попадает на входы загрузки регистров первого и второго выходов (тем самым по входам данных этих регистров в них ничего не поступает) и в логический элемент "НЕ" 61. На выходе логического элемента "НЕ" 61 появляется логическое значение 1 ("истина"), которая и подается на входы загрузки регистров 41-46, после чего в эти регистры поступают значения R1 = 5, R2 = 2, U1 = 0, U2 = 1, V1 = 1, V2 = -1, соответственно, из регистров 47-52. На этом первый шаг заканчивается и начинается второй шаг.
После второго шага в регистрах 41-46 оказываются, соответственно, значения R1 = 2, R2 = 1, U1 = 1, U2 = -1, V1 = -2, V2 = 3 и начинается третий шаг. В ходе третьего шага в регистрах 47-52 оказываются значения 1, 0, -2, 3, 5, -7, соответственно. После этого на выходе компаратора 60 появляется логическое значение 1 ("истина"), которое поступает на входы загрузки регистров первого и второго выхода и, тем самым, в этих регистрах появляются данные С = -2 и D =3 из регистров 49 и 50, соответственно, которые и появляются, соответственно, на первом выходе 39 и втором выходе 40 ОЕП 33.
Пример 10
Как указано выше в тексте описания (перед описанием сущности способа изготовления вслепую цифровой RSA-подписи по первому варианту), в примере 10 приведен еще один частный случай реализации ММЕП и его работы, проиллюстрированный фиг. 5. Изображенный на фиг. 5 ММЕП 78 имеет базовый вход 79 и соответствующий ему экспонентный вход 80, базовый вход 81 и соответствующий ему экспонентный вход 82, модульный вход 83 и один выход. ММЕП содержит регистры 84-91, умножитель 92, модулярный экспоненциатор 93, вычитатель 94, модулярный вычислитель частного 95, вычислитель частного 96, компаратор 97 и элемент "НЕ" 98. При этом базовый вход 79 соединен со входом данных регистра 86, второй базовый вход 81 соединен со входом данных регистра 87, экспонентный вход 80 соединен со входом данных регистра 84, экспонентный вход 82 соединен со входом данных регистра 85, а модульный вход 83 соединен с модульными входами модулярного вычислителя частного 95 и модулярного экспоненциатора 93. Кроме этого ММЕП 78 содержит не показанный на фиг. 5 регистр выхода, выход которого соединен с выходом ММЕП 78, а вход данных регистра выхода соединен с выходом регистра 90. Выход регистра 84 соединен с входом делимого 99 вычислителя частного 96 и со входом уменьшаемого 100 вычитателя 94. Выход регистра 85 соединен со входом делителя 101 вычислителя частного 96, со входом 102 умножителя 92 и со входом данных регистра 88. Выход регистра 86 соединен со входом делимого 103 модулярного вычислителя частного 95. Выход регистра 87 соединен со входом 104 модулярного экспоненциатора 93 и со входом данных регистра 90. Выход вычислителя частного 96 соединен со входом 105 умножителя 92 и с экспонентным входом 106 модулярного экспоненциатора 93. Выход умножителя 92 соединен со входом вычитаемого 107 вычитателя 94, а выход модулярного экспоненциатора 93 соединен со входом делителя 108 модулярного вычислителя частного 95. Выход вычитателя 94 соединен со входом данных регистра 89, а выход модулярного вычислителя частного 95 соединен со входом данных регистра 91. Выход регистра 88 соединен со входом данных регистра 84, выход регистра 89 соединен со входом данных регистра 85, выход регистра 90 соединен со входом данных регистра 86, но эти соединения не показаны. Выход регистра 89 соединен со входом 109 компаратора 97, а выход компаратора 97 соединен со входом загрузки регистра выхода и со входом логического элемента "НЕ" 98, выход которого соединен со входами загрузки регистров 84-87, но эти соединения не показаны. Кроме того ММЕП 78 включает схему начальной установки регистров 84-87, схему подачи нуля на вход 110 компаратора 97 и схему синхронизации, обеспечивающую пошаговый режим работы ММЕП, но эти схемы на фиг. 5 не показаны.
Конкретный пример работы ММЕП 78 состоит в следующем. Предположим, что на базовый вход 79 поданы данные X = 11, на базовый вход 81 поданы данные Y = 17, на экспонентный вход 80 поданы данные A = 7, на экспонентный вход 82 поданы данные В = 5, а на модульный вход 83 поданы данные N = 37. После этого схема начальной установки загружает в регистры 84-87, соответственно, значения: R1 = A = 7 со входа 80, R2 = B = 5 со входа 82, U1 = X = 11, U2 = Y = 17. Работа ММЕП проходит пошагово, что обеспечивается схемой синхронизации.
Детальное описание работы ММЕП 78 на первом шаге состоит в следующем. На вход делимого 99 и вход делителя 101 вычислителя частного 96 соответственно поступают данные R1 = 7 из регистра 84 и R2 = 5 из регистра 85, а на его выходе появляется неполное частное Q = 1 от деления R1 = 7 на R2 = 5. Данные Q = 1 появляются на входе 105 умножителя 92 и на экспонентном входе 106 модулярного экспоненциатора 93. На вход 102 умножителя 92 подаются данные R2 = 5 из регистра 85, а на его выходе появляются данные Q•R2 = 5, которые и поступают на вход вычитаемого 107 вычитателя 94. На вход уменьшаемого 100 вычитателя 94 подаются данные R1 = 7 из регистра 84, а на выходе вычитателя 94 появляются данные R1 - Q•R2 = 2, которые поступают в регистр 89. В регистр 88 поступают данные R2 = 5 из регистра 85. На базовый вход 104 модулярного экспоненциатора 93 подаются данные U2 = 17 из регистра 87, на модульный вход модулярного экспоненциатора 93 подаются данные N = 37 с модульного входа 83, а на его выходе появляются данные S = U2 Q (mod N) = 171 (mod 37) = 17, которые и попадают на вход делителя 108 модулярного вычислителя частного 95. На вход делимого 103 модулярного вычислителя частного 95 подаются данные U1 = 11 из регистра 86, а на выходе модулярного вычислителя частного 95 появляются данные U1•S-1 (mod N) = 11•17-1 (mod 37) = 5, которые поступают в регистр 91. В регистр 90 поступают данные U2 = 17 из регистра 87. На вход 109 компаратора 97 из регистра 89 поступают данные W = 2, на вход 110 компаратора 97 схемой подачи нуля подается ноль, а на его выходе появляется логическое значение 0 ("ложь"), которое попадает на входы загрузки регистров первого и второго выходов (тем самым по входам данных этих регистров в них ничего не поступает) и в логический элемент "НЕ" 98. На выходе логического элемента "НЕ" 98 появляется логическое значение 1 ("истина"), которая и подается на входы загрузки регистров 84-87, после чего в этих регистрах оказываются значения R1 = 5, R2 = 2, U1 = 17, U2 = 5, соответственно, из регистров 86-89. На этом первый шаг заканчивается и начинается второй шаг.
После второго шага в регистрах 84-87 оказываются значения R1 = 2, R2 = 1, U1 = 5, U2 = 14, после чего начинается третий шаг. В ходе третьего шага в регистрах 86-89 оказываются значения 1, 0, 14, 17, соответственно. После этого на выходе компаратора 97 появляется логическое значение 1 ("истина"), которое поступает на вход загрузки регистра выхода, после чего в этот регистр поступают данные Z = 14 из регистра 90, которые и появляются на выходе ММЕП 78.
Устройство для изготовления вслепую цифровой RSA-подписи по второму варианту, содержащее блок выбора маскировочного ключа с датчиком случайных чисел, блок маскировки с модулярным экспоненциатором, модульный вход которого соединен с модульным входом блока маскировки, а экспонентный вход которого соединен со входом маскировочного ключа блока маскировки, блок маскировки имеет вход исходных данных и один выход, который соединен со входом данных подписи блока подписи, который имеет вход секретного ключа и один выход, который соединен с входом данных демаскировки блока демаскировки, который имеет выход подписи, модульный вход, экспонентный вход и вход маскировочного ключа, к которому подсоединен выход блока маскировочного ключа, отличается от известного устройства для изготовления вслепую неожидаемой цифровой подписи, выбранного в качестве прототипа, тем, что базовый вход модулярного экспоненциатора блока маскировки соединен с входом исходных данных блока маскировки, а его выход соединен с выходом блока маскировки, блок демаскировки дополнительно имеет вход исходных данных и содержит модулярный мультипликативный евклидов преобразователь (ММЕП) с модульным входом, базовыми входами и соответствующими каждому из них экспонентными входами, причем модульный вход блока демаскировки соединен с модульным входом ММЕП, вход исходных данных блока демаскировки соединен с одним из базовых входов ММЕП, а вход данных демаскировки блока демаскировки соединен с другим базовым входом ММЕП, вход маскировочного ключа блока демаскировки соединен с экспонентным входом ММЕП, который соответствует базовому входу ММЕП, соединенному с входом данных демаскировки блока демаскировки, а экспонентный вход блока демаскировки соединен с экспонентным входом ММЕП, который соответствует базовому входу ММЕП, соединенному с входом исходных данных блока демаскировки, а выход блока демаскировки соединен с выходом ММЕП, блок выбора маскировочного ключа дополнительно содержит арифметический контроллер с двумя ограничительными входами, которые условно приняты за первый и второй ограничительные входы, причем арифметический контроллер соединен с датчиком случайных чисел, выход арифметического контроллера соединен с выходом блока выбора маскировочного ключа, а арифметический контроллер выполнен таким, что обеспечивает взаимную простоту выходных данных блока выбора маскировочного ключа относительно целых чисел, поданных на первый ограничительный вход арифметического контроллера, и делимость выходных данных блока выбора маскировочного ключа на тот наибольший делитель данных, поданных на второй его ограничительный вход, который взаимно прост относительно целых чисел, поданных на первый ограничительный вход арифметического контроллера.
Указанный выше технический результат в частных случаях конкретной реализации устройства может достигаться, кроме того, тем, что соединение арифметического контроллера с датчиком случайных чисел выполнено путем соединения выхода датчика случайных чисел со входом, условно принятым за вход пробных данных арифметического контроллера, а взаимная простота выхода блока выбора маскировочного ключа относительно целых чисел, поданных на первый ограничительный вход арифметического контроллера, и делимость выхода блока выбора маскировочного ключа на тот наибольший делитель данных, поданных на второй его ограничительный вход, который взаимно прост относительно целых чисел, поданных на первый ограничительный вход арифметического контроллера, обеспечена тем, что арифметический контроллер содержит вычислитель наибольшего общего делителя, вычислитель частного, умножитель и тестер взаимной простоты, причем первый ограничительный вход арифметического контроллера соединен со входом тестера взаимной простоты и со входом вычислителя наибольшего общего делителя, второй ограничительный вход арифметического контроллера соединен с другим входом вычислителя наибольшего общего делителя и со входом делимого вычислителя частного, вход пробных данных соединен с другим входом тестера взаимной простоты и со входом умножителя, выход тестера взаимной простоты соединен со входом загрузки умножителя, выход вычислителя наибольшего общего делителя соединен со входом делителя вычислителя частного, выход вычислителя частного соединен с аргументным входом умножителя, выход которого соединен с выходом арифметического контроллера.
Сущность устройства для изготовления вслепую цифровой RSA- подписи по второму варианту состоит в том, что с его помощью податель, при участии подписывающей стороны, может изготовить вслепую цифровую RSA-подпись для исходных данных по первому, второму, третьему и четвертому вариантам заявленного способа.
Для этого податель вводит исходные данные М на вход исходных данных, а известный из сообщения подписывающей стороны RSA-модуль N на модульный вход блока маскировки. Кроме того, податель вводит открытую RSA-экспоненту на первый ограничительный вход арифметического контроллера. Далее податель вводит на второй ограничительный вход арифметического контроллера маскирующий множитель, а при использовании заявленного устройства для реализации способов, заявленных по третьему и по четвертому вариантам, податель дополнительно вводит на второй ограничительный вход арифметического контроллера уменьшенный на единицу RSA-модуль. Маскировочный ключ R появляется на выходе блока выбора маскировочного ключа и поступает на вход маскировочного ключа блока маскировки, на выходе которого появляются замаскированные данные М'. Подписывающая сторона вводит на вход секретного ключа блока подписи секретный ключ (N, D), соответствующий выбранной открытой RSA-экспоненте E. На вход данных подписи блока подписи поступают замаскированные данные М', а на выходе блока подписи появляется цифровая RSA-подпись T' для замаскированных данных М', которая поступает на вход данных демаскировки блока демаскировки. Кроме того, податель вводит на модульный вход, вход исходных данных и экспонентный вход блока демаскировки, соответственно, RSA-модуль N, исходные данные М и открытую RSA-экспоненту E. Помимо этого, на вход маскировочного ключа блока демаскировки поступает маскировочный ключ R с выхода блока выбора маскировочного ключа. На выходе блока демаскировки появляется цифровая RSA-подпись S для исходных данных М.
При этом соединения между различными блоками могут быть выполнены посредством телекоммуникационных сетей, а сами блоки могут быть удалены друг от друга.
Единая совокупность признаков заявленного устройства по второму варианту, перечисленных выше, связана причинно- следственной связью с ранее изложенным техническим результатом изобретения, заключающимся в том, что при изготовлении вслепую неожидаемой цифровой RSA-подписи возможно использование неограниченного количества видов подписи; кроме того, не требуются растущие в зависимости от количества возможных видов подписи ресурсы, хранилища больших объемов данных и поиск в них, что, в свою очередь, приводит к ускорению и повышению надежности способа изготовления вслепую цифровой RSA-подписи.
Ниже приведен пример конкретной реализации устройства для изготовления вслепую цифровой RSA-подписи по второму варианту.
Пример 11
Частный случай реализации заявленного устройства по второму варианту проиллюстрирован фиг. 6, на которой изображено устройство для изготовления вслепую цифровой RSA-подписи, содержащее блок выбора маскировочного ключа 111, блок маскировки 2, блок подписи 3 и блок демаскировки 4. Блок выбора маскировочного ключа содержит датчик случайных чисел 5 и арифметический контроллер 112, имеющий первый ограничительный вход 113, второй ограничительный вход 114 и вход пробных данных 115, причем выход датчика случайных чисел соединен со входом пробных данных 115, а выход арифметического контроллера 112 соединен с выходом блока создания маскировочного ключа. Блок маскировки 2 имеет вход исходных данных 10, модульный вход 11, вход маскировочного ключа 12 и содержит не показанный на фиг. 6 модулярный экспоненциатор, причем вход исходных данных 10, вход маскировочного ключа 12 и модульный вход 11 блока маскировки соединены соответственно с базовым входом, экспонентным входом и модульным входом модулярного экспоненциатора. Блок подписи 3 имеет вход секретного ключа 13 и вход данных подписи 14, причем вход данных подписи 14 блока подписи 3 соединен с выходом блока маскировки 2. Блок демаскировки 4 имеет вход данных демаскировки 15, модульный вход 16, экспонентный вход 17, вход маскировочного ключа 18 и вход исходных данных 19 и содержит не показанный на фиг. 6 модулярный мультипликативный евклидов преобразователь (ММЕП), причем модульный вход 16 соединен с модульным входом ММЕП, вход исходных данных 19 соединен с одним из базовых входов ММЕП, а вход данных демаскировки 15 соединен с другим базовым входом ММЕП, вход маскировочного ключа 18 соединен с экспонентным входом ММЕП, соответствующим базовому входу ММЕП, соединенному с входом данных демаскировки 15, а экспонентный вход 17 соединен с экспонентным входом ММЕП, соответствующим базовому входу ММЕП, соединенному с входом исходных данных 19, а выход ММЕП соединен с выходом блока демаскировки.
Конкретный пример работы вышеописанного устройства для изготовления вслепую цифровой RSA-подписи по второму варианту состоит в следующем. Предположим, что подписывающая сторона выбрала секретные множители P = 659 и Q = 827, RSA-модуль N = 544993, открытую RSA-экспоненту E = 3, после чего сообщила RSA- модуль N, открытую RSA-экспоненту E всем заинтересованным сторонам. Предположим, что податель желает изготовить вслепую цифровую RSA-подпись исходных данных М = 123456. Для этого податель вводит исходные данные М = 123456 на вход исходных данных 10, а RSA-модуль N = 544993 на модульный вход 11 блока маскировки 2. Кроме того, податель вводит открытую RSA-экспоненту E = 3 на первый ограничительный вход 113 арифметического контроллера 112, а уменьшенный на единицу RSA-модуль N, то есть целое число 544992, на второй ограничительный вход 114 арифметического контроллера 112. Предположим, что на выходе блока выбора маскировочного ключа 111 появилось целое число R = 163679264. Целое число R = 163679264 поступает на вход маскировочного ключа 12 блока маскировки 2, на выходе которого появляются данные М' = 52602. Подписывающая сторона вводит на вход секретного ключа 13 блока подписи 3 секретный ключ (N, D), соответствующий открытой RSA-экспоненте, то есть D = 362339. На вход данных подписи 14 блока подписи 3 поступает целое число М' = 52602, а на выходе блока подписи 3 появляется целое число Т' = 447760, которое поступает на вход данных демаскировки 15 блока демаскировки 4. Кроме того, податель вводит на модульный вход 16, вход исходных данных 19 и экспонентный вход 17 блока демаскировки 4, соответственно, RSA-модуль N = 544993, исходные данные М = 123456 и открытую RSA-экспоненту E = 3. Помимо этого, на вход маскировочного ключа 18 блока демаскировки 4 поступает целое число R = 163679264. На выходе блока демаскировки появляются данные Т = 405712, которые и являются цифровой RSA-подписью для исходных данных М = 123456.
Кроме того, в приведенном ниже примере 12 описан частный случай реализации арифметического контроллера, содержащегося в блоке выбора маскировочного ключа заявленного устройства для изготовления вслепую цифровой RSA-подписи по второму варианту и приводит конкретный пример работы указанного блока выбора маскировочного ключа.
Пример 12
Пример проиллюстрирован фиг.7 и вышеуказанной фиг.6. На Фиг.7 изображен арифметический контроллер 112, который имеет вход пробных данных 115, первый ограничительный вход 113, второй ограничительный вход 114, один выход и содержит вычислитель наибольшего общего делителя 116, вычислитель частного 117, умножитель 118 и тестер взаимной простоты 119. При этом первый ограничительный вход 113 соединен со входом 120 тестера взаимной простоты и со входом 121 вычислителя наибольшего общего делителя 116, второй ограничительный вход 114 соединен со входом 122 вычислителя наибольшего общего делителя 116 и со входом делимого вычислителя частного 117, вход пробных данных 115 соединен со входом 123 тестера взаимной простоты и со входом 124 умножителя 118, выход тестера взаимной простоты 119 соединен со входом загрузки 125 умножителя 118, выход вычислителя наибольшего общего делителя 116 соединен со входом делителя вычислителя частного 117, выход вычислителя частного 117 соединен с аргументным входом 126 умножителя 118, выход которого соединен с выходом арифметического контроллера 112.
Конкретный пример работы блока выбора маскировочного ключа 111 вышеописанного устройства для изготовления вслепую цифровой RSA-подписи по второму варианту состоит в следующем. Предположим, что на выходе датчика случайных чисел 5 появляется целое число 1234, которое попадает на вход пробных данных 115 арифметического контроллера 112. Предположим, что на первый ограничительный вход 113 подано целое число 21, а на второй ограничительный вход 114 подано целое число 15. Целые числа 1234 и 21 поступают, соответственно, на входы 123 и 120 тестера взаимной простоты 119, на выходе которого появляется логическое значение 1 ("истина"). Это значение поступает на вход загрузки 125 умножителя 118, и тем самым умножитель 118 вбирает данные, поданные на его аргументные входы 124 и 126. При этом на вход 124 поступает целое число 1234 со входа пробных данных 115 арифметического контроллера 112. Целые числа 21 и 15 поступают, соответственно, на входы 121 и 122 вычислителя наибольшего общего делителя 116, на выходе которого появляется целое число 3. На входы делителя и делимого вычислителя частного 117 поступают соответственно целое число 3 с выхода вычислителя наибольшего общего делителя 116 и целое число 15 со второго ограничительного входа 114, а на выходе вычислителя частного 117 появляется целое число 5, которое поступает на вход 126 умножителя 118. На выходе умножителя 118 появляется целое число 6170, которое появляется на выходе арифметического контроллера 112 и на выходе блока выбора маскировочного ключа 111.
В качестве других частных случаев устройства по второму варианту отмечается возможность его реализации в виде многих иных разбиений содержащихся в нем вспомогательных устройств на блоки, которые не меняют сущности заявленного изобретения. Также возможно выполнять соединения между блоками путем пропускания этих соединений через дополнительные устройства. Среди таких дополнительных устройств могут быть, в частности, шифровальные, дешифровальные, кодирующие и декодирующие устройства. Кроме того, заявленное устройство может быть дополнено другими известными устройствами, в частности, устройствами для проверки RSA-подписи.
Список литературы
1. A. J. Menezes, P. С. Van Oorshot, S. A. Vanstone, Handbook of Applied Cryptography, CRC Press, 1997.
2. B. Schneier, Applied Cryptography: Protocols, Algorithms, and Source Code in C, John Wiley&Sons, New York, 2nd edition, 1996.
3. R. L. Rivest, A. Shamir, L.M. Adleman, Cryptographic Communications System and Method, U.S. Patent 4405829, 20 Sep. 1983.
4. D. Chaum, Blind signatures for untraceable payments, Advanced in Cryptology-Proceedings of Crypto 82, 1983, p. 199-203.
5. D. Chaum, Blind Signature Systems, U.S. Patent 4759063,19 Jul. 1988.
6. D. Chaum, Blind Unanticipated Signature Systems. U. S. Patent 4759064,19 Jul. 1988.
7. Д. Кнут, Искусство программирования для ЭВМ. Т. 2. Получисленные алгоритмы. - М.: Мир, 1977.
8. J. Oesterle, Versions effectives du theoreme de Chebotarev sous l'hypothese de Riemann generalisee, Soc. Math. De France, Asterisque 61, 1979, p. 165-167.






Изобретение относится к криптографии, в частности к изготовлению цифровой подписи, и может быть использовано в электронных системах массового обслуживания. Техническим результатом является создание способов изготовления вслепую цифровой RSA-подписи и устройств для их реализации, обеспечивающих непрослеживаемость и высокую неожидаемость при изготовлении цифровой RSA-подписи, а также допускали бы быстрое изготовление при сравнительно небольших ресурсах. Сущность изобретения состоит в создании способов маскировки исходных данных для использования в электронных системах массового обслуживания с неограниченным числом видов подписи, которые не требуют растущих в зависимости от числа используемых видов подписи технических ресурсов, хранилищ больших объемов данных и поиска в них, это позволяет ускорить и повысить надежность способа изготовления вслепую неожидаемой цифровой RSA-подписи, а также повышает достоверность непрослеживаемости за счет того, что свойства данных, обеспечивающих непрослеживаемость, могут быть проверены непосредственно самим подателем. Способ включает последовательно осуществляемые операции маскировки исходных данных посредством их RSA-шифрования и соответствующей демаскировки подписанных замаскированных данных. Реализация изобретения осуществляется устройством. 7 с. и 47 з.п.ф-лы, 7 ил.
| US 4759064 A, 19.07.1988 | |||
| RU 95106218 A1, 20.01.1997 | |||
| US 4759063 A1, 19.07.1988 | |||
| US 4405829 A, 20.09.1983 | |||
| СПОСОБ ШИФРОВАНИЯ ЦИФРОВОЙ ПОДПИСИ ДВОИЧНОГО СООБЩЕНИЯ (АЛБЕР-ПОДПИСЬ) | 1991 |
|
RU2030836C1 |
| RU 94001074 A1, 10.01.1996. | |||
Авторы
Даты
2000-07-20—Публикация
1998-09-29—Подача