Изобретение относится к передаче сообщений и может быть использовано для установления подлинности переданного цифрового сообщения и его автора при возникновении спора относительно авторства и подлинности сообщения.
Известны два класса способов формирования цифровой подписи. Первый класс способов использует для формирования цифровой подписи труднообратимые функции, например возведение в степень в конечных полях большой размерности (несколько сот бит). Эти способы имеют два существенных недостатка.
Во-первых, сложность подделки подписи определяется сложностью логарифмирования или сложностью разложения чисел в конечных полях. А эти математические задачи со временем имеют тенденцию к упрощению, и не исключена возможность появления способов их решения за практически приемлемое время. Выход в увеличении размерности используемого конечного поля. Однако, уже при 500-1000 бит (рекомендуются такие величины) становится существенной техническая сложность реализации операции возведения в степень. Это второй недостаток.
Другой класс способов для формирования цифровой подписи применяет устройства шифрования двоичной информации, использующие секретный ключ. Невозможность подделки подписи в этих способах гарантируется криптографической стойкостью устройств шифрования.
Известен способ цифровой побитной подписи двоичного сообщения с применением устройства шифрования двоичной информации, заключающийся в формировании устройством шифрования на личном секретном ключе отправителя для каждого из двух значений каждого бита передаваемого сообщения индивидуального n-битного ключа, последующем исключающем подделку преобразовании отправителем каждого бита сообщения в n-битную подпись устройством шифрования на соответствующем ранее выработанном индивидуальном n-битном ключе и в сравнении получателем n-битных подписей битов сообщения с имеющимися у него общедоступными и заранее выработанными отправителем и переданными доверенным лицом получателю n-битными контрольными подписями каждого значения каждого очередного передаваемого бита.
Данный способ для обеспечения вероятности подделки подписи отдельного бита порядка 2-n требует передачи отправителем подписи в n раз более длинной, чем сообщение, и хранения у получателя как самой подписи, так и общедоступной комбинации в 2n раз более длинной, чем сообщение, чтобы при возникновении спора относительно подлинности содержания и авторства сообщения служить доказательством для независимого арбитра. Такая процедура выработки подписи в n раз повышает избыточность передаваемого сообщения. Кроме того, при более или менее интенсивной передаче несколько килобайтных сообщений получатель должен хранить общедоступные контрольные комбинации громадных размеров.
Целью настоящего изобретения является сокращение до разумных размеров длин передаваемой отправителем подписи и хранящейся у получателя контрольной комбинации.
Поставленная цель достигается тем, что сообщение предварительно свертывает в m-битную комбинацию устройством шифрования с использованием в качестве ключа самого передаваемого сообщения, каждый бит свертки подписывают известным способом n битами, mn битную подпись вместе с m неиспользованными n-битными ключами инверсных значений m бит свертки и номером сообщения передают получателю, на приемном конце полученную 2mn-битную комбинацию свертывают в n-битную комбинацию устройством шифрования с использованием в качестве ключа самой принятой 2mn-битной комбинации и сравнивают с хранящейся у получателя точно так же предварительно выработанной отправителем и переданной с доверенным лицом получателю n-битной контрольной комбинацией данного номера сообщения.
В свертке передаваемого сообщения одновременно подписывают по r бит, для чего для каждой группы из r бит из личного секретного ключа отправителя при помощи устройства шифрования формируют по два различных ключа, затем очередные r бит свертки преобразуют устройством шифрования на первом ключе столько раз, каково численное значение этих r бит, а на втором ключе количество раз, дополняющее предыдущее до числа 2r-1, причем для очередного преобразования в качестве ключа используется полученная на предыдущем шаге n-битная комбинация, передают получателю выработанную таким образом 2mn/r-битную подпись, на приемном конце свертывают 2mn/r-битную подпись описанным способом в n-битную комбинацию и сравнивают с хранящейся у получателя точно так же предварительно выработанной отправителем и переданной с доверенным лицом получателю n-битной контрольной комбинацией.
Выработанное предварительно n-битные контрольные комбинации всех Q=2q номеров сообщений свертывают парами описанным способом в 2q-1n-битных комбинаций q-1-го уровня, полученные 2q-1 n-битные комбинации q-1-го уровня снова свертывают парами в 2q-2 n-битных комбинаций q-2-го уровня, затем снова свертывают, и так q раз, пока не останется одна общедоступная n-битная комбинация 0-го уровня, которую с доверенным лицом заранее передают получателю, а при передаче сообщения ему передают вместе с 2mn/r-битной подписью n-битную контрольную комбинацию, парную для получения комбинации q-1-го уровня, а также q-1 комбинаций q-1, q-2,...,1-го уровней, дополняющих до пар при получении комбинаций следующего уровня, полученную на приеме подпись свертывают описанным способом, n-битную комбинацию снова свертывают с принятой парной n-битной комбинацией, результат свертывают с принятой парной комбинацией q-1-го уровня, и так q раз, пока не задействуют все q принятых дополняющих до пар n-битных комбинаций, полученную в результате n-битную комбинацию сравнивают с общедоступной n-битной комбинацией, хранящейся у получателя.
Свертывание N-битного сообщения в m-битную, m<<N, свертку уменьшает размер подписи в N/2m раз по сравнению с требуемым в прототипе. Свертывание подписи в n-битную комбинацию требует хранения у получателя всего лишь n контрольных бит на каждое сообщение. Если в свертке подписывать одновременно по r бит, то размер передаваемой подписи уменьшится в r раз. Если осуществить древовидное попарное свертывание контрольных комбинаций всех сообщений, то у получателя достаточно хранить лишь одну n-битную общедоступную контрольную комбинацию.
Сложность подделки подписи определяется минимальным из чисел m (длина свертки), n (длина общедоступной контрольной комбинации) и s (длина секретного ключа). Поэтому все эти числа целесообразно выбирать одинаковыми, то есть m=n=s. При этом, рекомендуется ограничиться максимальным значением 128. Так, при n= 64 сложность подделки подписи определяется перебором 264≈1019 ключей, а при n=128 надо перебрать 2128≈1039 ключей, что абсолютно нереально.
Для примера рассмотрим случай n=m=s=64.
N-битный открытый текст Т делится на блоки по 16 байт - Т1, Т2,...,ТN'.
Открытый текст Т свертывается в 64-битную комбинацию В следующим образом:
В= F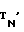 (FTN'-1(...FT1V(0)...)), где FТi(Х) - результат шифрования алгоритмом Албер 8-байтной комбинации Х на 16-байтном ключе Тi.
(FTN'-1(...FT1V(0)...)), где FТi(Х) - результат шифрования алгоритмом Албер 8-байтной комбинации Х на 16-байтном ключе Тi.
Криптографическая стойкость алгоритма Албер гарантирует сложность подбора другого сообщения Т'≠Т с той же сверткой В на уровне 264переборов различных Т'.
Если К - 8-байтный секретный ключ отправителя, то группу из 128 индивидуальных ключей (по паре для каждого бита свертки)
k1,0t, k1,1t, k2,0t, k2,1t,...,k64,0t,k64,1t (1) для t-го сообщения вырабатывают следующим образом:
k1,0t=Fk(t), k1,1t=Fk(kt1,0),
k2,0t=Fk(k1,1t), k2,1t=Fk(k2,0t),
k64,0t=Fk(k63,1t), k64,1t=Fk(k64,0t), где t=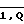 , - номер сообщения, которое будет подписываться с использованием этой группы ключей.
, - номер сообщения, которое будет подписываться с использованием этой группы ключей.
В так выработанной группе ключей для определения любого ключа ki,j, 1 ≅ i ≅ 64, j=0,1, при известных остальных ключах (кроме секретного ключа К) необходимо вычислить секретный ключ К, для чего требуется перебор 264 всех возможных вариантов ключа К.
Общедоступные 64-битные контрольные комбинации хt, 1 ≅ t ≅ Q, для Q сообщений вырабатывают заранее. Для этого сначала формируют из секретного ключа t-ую группу индивидуальных ключей (1). Затем на каждой паре индивидуальных ключей kti,0, kti,1 шифруют 0 и 1 (например, комбинации из 64 нулей или 64 единиц). Полученные 128 8-битных блоков t t
F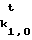 (0)=р1,0, F
(0)=р1,0, F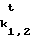 (1)=р1,1,...,
(1)=р1,1,...,
F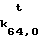 (0)= рt, F
(0)= рt, F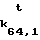 (1)=рt свертывают точно так же, как и сообщение Т. Последовательность
(1)=рt свертывают точно так же, как и сообщение Т. Последовательность
р1,0t, р1,1t,...,р64,0t, р64,1t (2) разбивают на блоки р1, р2,..,р64 по 16 байт и формируют контрольную комбинацию
хt=Fр64(Fр63) (...Fр1(0)...)).
Общедоступные контрольные комбинации х1,х2,...,хQ передают с доверенным лицом всем получателям.
Свертку В= (b1,...,b64), bi=0,1, 1 ≅ i ≅ 64, t-го сообщения Т подписывают следующим образом. Сначала формируют 128 64-битных блоков
b1,0, b1,1, ...,b64,0, b64,1, (3) где bi,0= F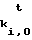 (0), bi,1=ki
(0), bi,1=ki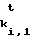 (1), если bi=1.
(1), если bi=1.
128 блоков (3) составляют 2*64*64-битную подпись, передаваемую получателю.
На приеме из полученных 128 блоков (3) формируют последовательность (2). Для этого сначала свертывают принятое сообщение Т и получают свертку В=(b1,...,b64). Получатель знает,
что если bi=0, то bi,0= F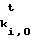 (0), bi,1=ki
(0), bi,1=ki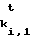 (1), поэтому рi
(1), поэтому рi
Сформированную последовательность (2) свертывают и результат ytсравнивают с контрольной комбинацией хt. Равенство yt=хt удостоверяет отправителя и сообщение. Неравенство yt≠хt говорит получателю о том, что кто-то пытался изменить сообщение, подпись или имя отправителя.
Сложность восстановления ключа k из равенства b=Fk(а) при известных а и b определяется числом 264 переборов всех вариантов ключа k. Поэтому для замены пары k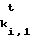 (1) на пару F
(1) на пару F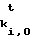 (0), k
(0), k
В свертке В=(b1,...,b64) сообщения Т можно подписывать не отдельные биты b1,...,b64, а сразу группы по r бит с1=(b1,...,br), с2=(br+1,...,b2r),.. .
Как и в побитном случае, сначала формируют 64/r пар индивидуальных ключей
k
k
. . . . . . . .
Затем с их помощью формируют общедоступную 64-битную контрольную комбинацию хt. Для этого на каждой паре ключей k
F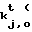 0)=c0,1, F
0)=c0,1, F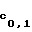 0)= с0,2,...,F
0)= с0,2,...,F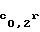

 (0)=
(0)=
=c0,2r -1=р
F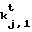 (0)=с1,1, F
(0)=с1,1, F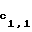 0)=с1,2,..., F
0)=с1,2,..., F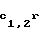

 (0)=
(0)=
=c1,2r -1=рj
Последовательность
р
Подпись C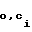 , c1,2r -1-
, c1,2r -1-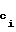 r-битной группы сi, i=1,...,64/r, свертки В сообщения Т формируют следующим образом F
r-битной группы сi, i=1,...,64/r, свертки В сообщения Т формируют следующим образом F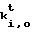 (0)=с0,1, F
(0)=с0,1, F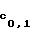 0)=с0,2,..., Fc
0)=с0,2,..., Fc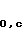
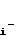
 0)=
0)=
= c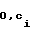 ,
,
F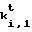 (0)=с1,1, F
(0)=с1,1, F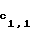 (0)=с1,2,...,F2r
(0)=с1,2,...,F2r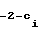 (0)=
(0)=
=c1,2r -1-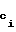 .
.
Получателю передают 128/r 64-битных комбинаций c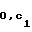 , c1,2r -1-
, c1,2r -1-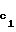 , c
, c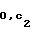 , c1,2r -1-
, c1,2r -1-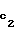 ,...
,...
На приеме сначала свертывают сообщение Т в свертку В и разбивают ее на r-битные группы с1, с2,.. Затем шифруют принятые комбинации c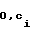 еще 2r-1-сi раз, а комбинации c1,2r -1-
еще 2r-1-сi раз, а комбинации c1,2r -1-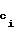 еще сi раз, то есть:
еще сi раз, то есть:
F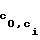 (0)=c
(0)=c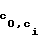

 ,...,F
,...,F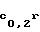

 (0)=
(0)=
= c0,2r -1 =р
F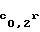



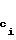 (0)=c
(0)=c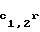

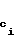 ,..., F
,..., F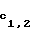 r -2(0)=
r -2(0)=
= c1,2r -1 =р
Аналогичным образом докручивают до р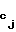 подписи. Полученную последовательность (6) разбивают на блоки по 16 байт и свертывают в 64-битную комбинацию yt, которую сравнивают с общедоступной контрольной комбинацией хt t-го сообщения.
подписи. Полученную последовательность (6) разбивают на блоки по 16 байт и свертывают в 64-битную комбинацию yt, которую сравнивают с общедоступной контрольной комбинацией хt t-го сообщения.
Чтобы подделать подпись r-битной группы сj', зная подпись группы сj= сj', надо по цепочке (4), если сj'<сj, либо по цепочке (5), если сj'>сj, пройти влево. Это требует определения ключа в схеме Албер, которое можно осуществить перебором 264 его вариантов.
Сократить количество общедоступных 64-битных контрольных комбинаций, хранящихся у получателей сообщений, можно следующим образом. Пусть общее количество сообщений равно Q= 2q. Tогда заранее из 64-битных контрольных комбинаций р1, р2,...,рQ формируют 2q-1 64-битных комбинаций
р1q-1= F (0), р2q-1= F
(0), р2q-1= F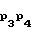 (0),..., p
(0),..., p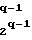 = F
= F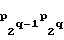 (0) q-1-го уровня. Затем и 2q-1 комбинаций р1q-1 р2q-1..., p
(0) q-1-го уровня. Затем и 2q-1 комбинаций р1q-1 р2q-1..., p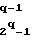 формируют 2q-2 64-битных комбинаций
формируют 2q-2 64-битных комбинаций
p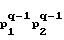 (0), p
(0), p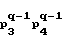 (0),...,p
(0),...,p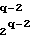 =F
=F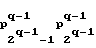 (0) q-2-го уровня. И так далее, до 0-го уровня:
(0) q-2-го уровня. И так далее, до 0-го уровня:
p0=F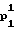
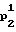 (0).
(0).
64-битная комбинация р0 является общедоступной контрольной комбинацией для всех Q=2q сообщений и ее с доверенным лицом передают получателям.
t-ое сообщение Т подписывают описанным выше образом и подпись вместе с q комбинациями ptq, p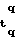

 ,...,p
,...,p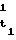 всех уровней, дополняющих до пары в проделанной заранее процедуре получения комбинации следующего уровня, передают получателю. На приеме формируют комбинацию рt, а затем цепочку комбинаций
всех уровней, дополняющих до пары в проделанной заранее процедуре получения комбинации следующего уровня, передают получателю. На приеме формируют комбинацию рt, а затем цепочку комбинаций
F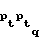 (0) = pq-1, F
(0) = pq-1, F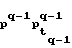 (0) = pq-2,..., F
(0) = pq-2,..., F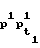 (0) = x0.
(0) = x0.
Комбинацию х0 сравнивают с контрольной комбинацией р0 и по результату сравнения делают вывод о подлинности подписи.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ФОРМИРОВАНИЯ N-БИТНОЙ КОНТРОЛЬНОЙ КОМБИНАЦИИ N-БИТНОЙ ДВОИЧНОЙ ИНФОРМАЦИИ | 1994 |
|
RU2114463C1 |
| УСТРОЙСТВО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ "АЛБЕР" | 1991 |
|
RU2007884C1 |
| СПОСОБ ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ И УСТРОЙСТВО ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА - "АЛБЕР" | 1994 |
|
RU2099890C1 |
| УСТРОЙСТВО ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ "АЛБЕР" | 1991 |
|
RU2024209C1 |
| СИСТЕМА И СПОСОБ ЗАЩИТЫ ИНФОРМАЦИИ | 2018 |
|
RU2719423C1 |
| СПОСОБ ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1995 |
|
RU2097931C1 |
| СПОСОБ ШИФРОВАНИЯ ДВОИЧНОЙ ИНФОРМАЦИИ | 1992 |
|
RU2032990C1 |
| СИСТЕМА И СПОСОБ ДЛЯ ЗАЩИТЫ ИНФОРМАЦИИ | 2018 |
|
RU2721959C1 |
| СИСТЕМА И СПОСОБ ЗАЩИТЫ ИНФОРМАЦИИ | 2018 |
|
RU2716740C1 |
| СПОСОБ ДОСТАВКИ КЛЮЧА С ПРОВЕРКОЙ ПОДЛИННОСТИ КОРРЕСПОНДЕНТА РАДИОСЕТИ | 2016 |
|
RU2654122C2 |
Использование: в технике передачи сообщений. Сущность изобретения: с помощью способа шифрования цифровой подписи двоичного сообщения установливают подлинность переданного цифрового сообщения и его автора при возникновении спора оносительно авторства и подлинности сообщения. Способ обеспечивает гарантированную криптографическую надежность подписи при разумных ее размерах. 3 з.п. ф-лы.
СПОСОБ ШИФРОВАНИЯ ЦИФРОВОЙ ПОДПИСИ ДВОИЧНОГО СООБЩЕНИЯ (АЛБЕР-ПОДПИСЬ).
| W | |||
| Diffie and M.E.Hellman "New direction in cryptografy "IEEE, Traus, and Informations Theory, IT -22, 6 (Nov.1976). |
Авторы
Даты
1995-03-10—Публикация
1991-12-26—Подача