Изобретение относится к расчетно-экспериментальным методам определения зависимости между нагрузкой и перемещением пластин по результатам испытания ее модели и может быть использовано при диагностике напряженно-деформированного состояния строительных и машиностроительных конструкций, а также в лабораторном практикуме по сопротивлению материалов и строительной механике.
Известен способ определения перемещений конструкции с помощью испытания ее модели [1], который заключается в изготовлении по критериям геометрического подобия модели, закреплении ее и нагружении подобно заданной конструкции и определении перемещений заданной конструкции по соответственным перемещениям модели с учетом соотношений физико-механических характеристик заданной конструкции и модели (плотность материала, модуль упругости, коэффициент Пуассона).
Недостаток этого способа заключается в значительной трудоемкости при моделировании ее граничных условий и условий загружения модели, а иногда и невозможности такого моделирования из-за неопределенности граничных условий конструкции, стоящей непосредственно в сооружении.
Известен способ определения перемещения конструкции в виде пластин под нагрузкой с любыми граничными условиями [2], принятый в качестве прототипа, который заключается в динамическом испытании заданной конструкции и определении ее частоты колебаний основного тона (резонансной частоты), в изготовлении модели-пластинки по критериям геометрического подобия, закреплении ее по контуру с условием выполнения однородных граничных условий, динамическом и статическом ее испытании с целью нахождения резонансной частоты колебаний основного тона и величины максимального перемещения и определении максимального прогиба заданной пластинки с учетом соотношений ее физико-механических характеристик с соответствующими характеристиками модели (масса единицы площади, интенсивность поперечной нагрузки, резонансная частота колебаний).
Недостаток этого способа заключается в необходимости соблюдения условия геометрического подобия заданной пластинки и пластинки-модели, что во многих случаях сопряжено с определенными трудностями при изготовлении модели.
Задача, на решение которой направлено изобретение заключается в упрощении требований к соблюдению условий геометрического подобия заданной пластинки и пластинки-модели и снижении трудоемкости модельных испытаний.
Это достигается тем, что в предлагаемом способе определения максимального перемещения элемента конструкции в виде пластинки при поперечном изгибе, под действием равномерно распределенной нагрузки, заключающемся в динамическом испытании заданной конструкции и определении ее частоты колебаний основного тона (резонансной частоты), в изготовлении пластинки-модели, закреплении ее по контуру и выполнении однородных граничных условий, динамическом и статическом испытании модели, нахождении при этом ее резонансной частоты колебаний основного тона и величины максимального перемещения и расчетном определении максимального прогиба заданной пластинки с учетом соотношений ее физико-механических и геометрических характеристик с соответствующими характеристиками модели (масса единицы площади, интенсивность поперечной нагрузки, резонансная частота колебаний, площадь) пластику-модель выполняют любой, удобной для ее изготовления и осуществления однородных граничных условий при испытании, с соблюдением условия равенства (Kf)з.п = (Kf)м, где (Kf)з.п - коэффициент формы заданной пластинки, (Kf)м - коэффициент формы пластинки-модели.
Сущность изобретения поясняется чертежом, заимствованным из монографии, на котором в обобщенном виде приведены графики изменения максимального прогиба пластинок с однородными граничными условиями, находящихся под действием равномерно распределенной нагрузки w0 (схема а), круговой частоты свободных колебаний по основному тону ω (схема б) и произведения w0ω2 (схема в) в зависимости от изменения коэффициента формы области Kf.
Коэффициент формы области определяется контурным интегралом
где ds - линейный элемент контура области и h - высота, опущенная из центра полярной системы координат на касательную к переменной точке контура, являются количественными характеристиками формы области. Для многоугольных областей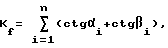
где n - количество сторон многоугольника; αi и βi - углы, образованные лучами, проведенными из полюса в углы многоугольника; для областей с криволинейным контуром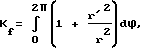
где r = r(ϕ) - полярное уравнение контура области.
Из графиков, приведенных на чертеже, следует важная закономерность, носящая фундаментальный характер [3] : для упругих изотропных пластинок постоянной толщины и произвольной формы независимо от вида граничных условий произведение максимального статического прогиба от действия равномерно распределенной нагрузки на квадрат основной круговой частоты их колебаний в ненагруженном состоянии вырождается в линию и ограничено с двух сторон: верхняя граница этого произведения равна (4/π2) и соответствует круглым пластинам, а нижняя равна (4π) и соответствует бесконечно вытянутым пластинам (балкам), то есть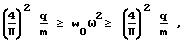
где q - интенсивность равномерно распределенной нагрузки; m - масса единицы площади пластинки. Из указанной закономерности следует, что для заданной пластинки определенной формы (с заданным коэффициентом формы) и пластинки-модели любой другой формы, но с тем же коэффициентом формы будут справедливы следующие соотношения:
w0ω2 = Cq/m; (w0)мω
где индекс "м" соответствует характеристикам пластинки-модели. Откуда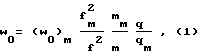
где f= ω/(2π) - измеряемая частота колебаний.
Таким образом, при изготовлении пластинки-модели можно не соблюдать условия геометрического подобия заданной пластинки и пластинки-модели, необходимо лишь выполнить условия равенства их коэффициентов формы
(Kf)з.п=(Kf)м.
При выборе формы пластинки-модели следует руководствоваться требованиями снижения трудоемкости, простотой и удобством ее изготовления.
Способ реализуют следующим образом.
В заданной пластинке, находящейся в составе сооружения, определяют массу единицы площади, вычисляют коэффициент формы, возбуждают в ней свободные колебания, например, с помощью механического удара и измеряют частоту колебаний основного тона f с помощью вибрографа, например с помощью частотомера Ч3-33.
Из любого упругого материала изготавливают пластинку-модель произвольной формы при соблюдении условия равенства (Kf)з.п =(Kf)м, определяют ее массу mм, закрепляют по краям с соблюдением однородных граничных условий, например шарнирно, производят ее динамические испытания в ненагруженном состоянии и статические испытания равномерно распределенной нагрузкой. В результате испытаний определяют основную частоту колебаний fм и максимальный прогиб (w0)м, например, с помощью прогибомеров индикаторного типа. Максимальное перемещение заданной пластинки определяют расчетным путем по формуле (1).
Пример реализации способа. Необходимо определить максимальный прогиб железобетонной шарнирно опертой плиты постоянной толщины в виде равнобочной трапеции (угол при основании α = π/3, длина нижнего основания а1 = 6 м, длина верхнего основания а2 = a1/2 = 3 м, толщина H = 16 см, модуль упругости железобетона E = 3,2•104 МПа, коэффициент Пуассона ν = 0,25) от действия равномерно распределенной нагрузки q = 5 кН/м2. Коэффициент формы такой пластинки [3] (Kf)з.п =9,9497, а масса единицы площади m = 320 кг/м2.
В этой плите, установленной и закрепленной на стенде, возбудили свободные колебания и определили резонансную частоту колебаний, которая оказалась равной f= 36,12 Гц.
Из дюралиминия была изготовлена пластинка-модель с размерами lvxbvxHv - 0,29х0,15х0,003 м (E = 7,3•104 МПа, γ = =2,79 кг/дм3, ν = 0,34, mм = 8,37 кг/м2). Для такой пластинки [3]:
(Kf)м = 4(0,3/0,15+0,15/0,3) = 10 ≈ 9,9497.
Закрепив края пластинки-модели шарнирно и проведя динамические испытания, определили ее основную частоту колебаний fм = 40,85 Гц. Нагружая модель равномерно распределенной нагрузкой интенсивностью qм = 0,1 кН/м2, определили ее максимальный прогиб (w0)м = 0,27 см.
Подставляя исходные и полученные экспериментально данные в выражение (1), определили: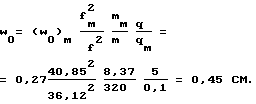
Максимальный прогиб заданной железобетонной плиты, определенный экспериментально, равен w0 = 0,48 см, что отличается от результата, полученного расчетно-экспериментальным путем на 6,25%.
Таким образом, применение предлагаемого способа сокращает время его проведения и снижает трудоемкость практической реализации за счет упрощения требований к моделированию формы пластинки.
Источники информации
1. Справочник по динамике сооружений / Под ред. профессоров Б.Г.Коренева и И.М.Рабиновича. М.: Стройиздат, 1972, с. 488-500.
2. Коробко В. И. , Идрисов Н.Д. Способ определения перемещения плоских элементов конструкций под нагрузкой. Патент РФ N 1647345, М. Кл.4 G 01 N 3/08, 1989.
3. Коробко В.И. Изопериметрический метод в строительной механике: Теоретические основы изопериметрического метода. - Т.1.- М.: Изд-во АСВ, 1997, с. 353.
Изобретение относится к расчетно-экспериментальным методам определения зависимости между нагрузкой и перемещением пластин по результатам испытания ее модели и может быть использовано при диагностике напряженно-деформированного состояния строительных и машиностроительных конструкций. Способ заключается в динамическом испытании заданной конструкции и определении ее частоты колебаний основного тона (резонансной частоты), в изготовлении пластинки-модели, закреплении ее по контуру и выполнении однородных граничных условий, динамическом и статическом испытаниях модели, измерении ее резонансной частоты колебаний основного тона и величины максимального перемещения и расчетном определении максимального прогиба заданной пластинки, причем пластинку-модель выбирают любой формы с соблюдением условия равенства коэффициента формы заданной пластинки и пластинки-модели. Технический результат - упрощение требований к соблюдению условий геометрического подобия заданной пластинки и пластинки-модели и снижение трудоемкости модельных испытаний. 1 ил.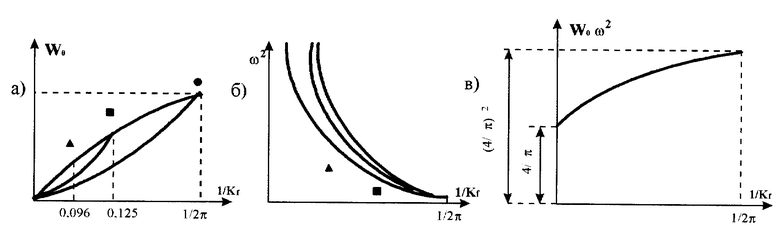
Способ определения максимального перемещения элемента конструкции в виде пластинки при поперечном изгибе под действием равномерно распределенной нагрузки, заключающийся в динамическом испытании заданной конструкции и определении ее частоты колебаний основного тона (резонансной частоты), в изготовлении пластинки-модели, закреплении ее по контуру и выполнении однородных граничных условий, динамическом и статическом испытаниях модели, измерении ее резонансной частоты колебаний основного тона и величины максимального перемещения и расчетном определении максимального прогиба заданной пластинки с учетом соотношений ее физико-механических характеристик с соответствующими характеристиками модели (масса единицы площади, интенсивность поперечной нагрузки, резонансная частота колебаний, площадь), отличающийся тем, что пластинку-модель выбирают произвольной формы с соблюдением условия равенства (Кf)з.п = (Кf)м, где (Кf)з.п - коэффициент формы заданной пластинки, (Кf)м - коэффициент формы пластинки-модели.
| Способ определения перемещения элемента конструкции под нагрузкой | 1986 |
|
SU1394110A1 |
| Способ определения перемещения плоских элементов конструкции под нагрузкой | 1989 |
|
SU1647345A1 |
| КОРОБКО В.И | |||
| Изопериметрический метод в строительной механике | |||
| Теоретические основы изопериметрического метода | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| - М.: Изд-во АСВ, 1997, с.353 | |||
| Справочник по динамике сооружений / Под ред | |||
| профессоров Б.Г | |||
| Коренева и И.М.Рабиновича | |||
| - М.: Стройиздат, 1972, с | |||
| Способ и прибор для акустического исследования земных напластований | 1923 |
|
SU488A1 |
Авторы
Даты
2000-10-10—Публикация
1999-04-27—Подача