Изобретение относится к области строительства и предназначено для определения оптимального числа нагелей в составных деревянных конструкциях балочного типа.
Известен теоретический способ определения количества нагелей n в симметричном соединении при их равномерном расположении по длине балки по формуле [1, с.202]:
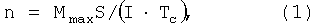
где Mmax - максимальный изгибающий момент в балке; S - статический момент площади слоя выше соединительного шва; I - момент инерции сечения балки как цельного; Tc - наименьшая расчетная несущая способность нагеля, определяемая по таблицам СНиП [2] в зависимости от материала нагеля.
Этот способ имеет недостаток, который заключается в том, что сдвигающее усилие N=MmaxS/I соответствует балке со сплошным сечением. Действительный же закон распределения сдвигающего усилия в составных балках зависит от числа нагелей и места их расположения. Поэтому по формуле (1) получается завышенное количество нагелей.
Задача, на решение которой направлено изобретение, состоит в разработке способа экспериментального определения оптимального количества нагелей в составных балках с использованием их моделей.
Это достигается тем, что в способе определения оптимального количества нагелей в составной деревянной балке изготавливают ее модель с соблюдением условий геометрического и физико-механического подобия, устанавливают на ней минимально возможное количестве нагелей, закрепляют модель на испытательном стенде согласно условиям эксплуатации балки, нагружают ее равномерно распределенной нагрузкой, равной по условиям физического подобия расчетной, измеряют максимальный прогиб, разгружают модель, устанавливают дополнительные нагели посредине между ранее установленными нагелями, повторяют операций нагружения, измерения и разгружения и выполняют весь цикл статических испытаний при поэтапном увеличении количества нагелей до стабилизации измеряемой величины максимального прогиба. По результатам статических испытаний строят графическую зависимость «максимальный прогиб - отношение числа поставленных нагелей на каждом этапе испытаний к максимальному числу использованных нагелей», проводят анализ кривых и более точно определяют начало участка стабилизации максимального прогиба, по которому вычисляют оптимальное количество нагелей для рассматриваемой модели и соответственно натурной балки.
Такого же результата можно достичь, если в способе определения оптимального количества нагелей в составной деревянной балке изготовить ее модель с соблюдением условий геометрического и физико-механического подобия, установить минимально возможное количество нагелей, закрепить модель на испытательном стенде согласно условиям эксплуатации балки, возбудить в ней поперечные собственные (или вынужденные) колебания, измерить основную (или первую резонансную) частоту этих колебаний, затем установить дополнительные нагели посредине между ранее установленными нагелями, повторить операции возбуждения колебаний и измерения их частоты и далее выполнить весь цикл динамических испытаний при поэтапном увеличении количества нагелей до стабилизации измеряемой величины основной (или первой резонансной) частоты колебаний; затем по результатам динамических испытаний следует построить графическую зависимость «основная (или первая резонансная) частота колебаний - отношение числа поставленных нагелей на каждом этапе испытаний к максимальному числу использованных нагелей», провести анализ кривых и более точно определить начало участка стабилизации частоты колебаний, по которому вычислить оптимальное количество нагелей для рассматриваемой модели и соответственно натурной балки.
Осуществление заявляемых способов поясняется чертежом, на котором представлены графики изменения максимального прогиба w0 и первой резонансной частоты колебаний ω в зависимости от отношения количества нагелей на модели nнагелей к максимальному количеству нагелей nmax, использованных при испытаниях.
Постепенное увеличение количества нагелей, используемых при изготовлении составных балок, ведет к увеличению их изгибной жесткости и, следовательно, к уменьшению статического прогиба w0 при нагружении балок равномерно распределенной нагрузкой и к увеличению основной (или первой резонансной) частоты колебаний ω в ненагруженном состоянии. Как показали эксперименты (см. чертеж), графики функций w0-nнагелей/nmax=k и функций ω-k для балок с различными граничными условиями асимптотически приближаются к постоянному значению при стремлении количества нагелей к бесконечности, соответствующему балкам со сплошным сечением. Причем стабилизация контролируемых параметров начинается достаточно быстро при малом количестве используемых нагелей. Поэтому оптимальным можно считать такое количество нагелей в составной балке, при котором процесс стабилизации рассматриваемых кривых считается установившимся.
Для определения оптимального количества нагелей использовать натурную составную балку нерационально, Целесообразно использовать модель такой балки, выполненную с соблюдением условий геометрического и физико-механического подобия [3]. Поэтому для реализации предлагаемых способов необходимо изготовить модели конструкций и их испытания проводить при постепенном увеличении числа нагелей. Экспериментальные исследования следует завершить построением функциональных зависимостей w0-k и ω-k их анализом для выявления начала участка стабилизации контролируемых параметров.
Способ осуществляется следующим образом. Для заданной составной балки с известными физическими и геометрическими характеристиками каждого из ее слоев изготавливают модель по условиям геометрического и физико-механического подобия. Модель устанавливают на стенде, закрепляют ее концы согласно условиям эксплуатации реальной конструкции в сооружении и устанавливает минимально возможное число нагелей - 3 у опор и в середине пролета.
Далее модель нагружают равномерно распределенной нагрузкой q, равной по условиям физического подобия расчетной для натурной балки, и измеряют ее максимальный прогиб w0: для модели с шарнирными или жестко защемленными опорами - в середине пролета; для модели с одной шарнирной и одной жестко защемленной опорами - на расстоянии 0,67L (где L - пролет модели) от шарнирной опоры.
После статических испытаний модель разгружают и устанавливают дополнительные нагели, располагая их равномерно между установленными ранее нагелями. Затем изложенную выше процедуру статических испытаний повторяют на каждом этапе установки дополнительных нагелей.
По результатам полученных измерений строят графическую зависимость w0-k (см. чертеж), анализируя которую выявляют участок стабилизации кривой, когда установка новых нагелей практически не изменяет максимального прогиба модели. Левая граница такого участка соответствует оптимальному числу нагелей в модели.
Соблюдая условия геометрического и физико-механического подобия, полученные результаты соотносят с параметрами реальной конструкции.
Аналогично, минимально возможное число нагелей можно определить по результатам динамических испытаний модели в ненагруженном состоянии, при проведении которых в той же последовательности, что и в первом случае, измеряют основную (или первую резонансную) частоту колебаний модели.
Примеры реализации способа
Способ статического нагружения моделей. В качестве моделей были изготовлены составные двухслойные деревянные балки длиной 2900 мм и сечениями 100×50+50×50 мм (ширина моделей 50 мм). Таких моделей было изготовлено три штуки для каждого вида граничных условий.
Модели последовательно устанавливались и закреплялись на специальном стенде, нагружались тарировочными грузами по 4 кг в шести равноудаленных ее сечениях, что соответствовало эквивалентной интенсивности равномерно распределенной нагрузки 82,76 Н/м. После нагружения измерялись максимальные прогибы прогибомером индикаторного типа с ценой деления 0,001 мм. После разгрузки устанавливались дополнительные нагели, и статические испытания повторялись вновь. Результаты испытаний приведены в таблице 1 (в колонке 3).
По результатам статических испытаний построены графики w0-k, которые представлены на чертеже пунктирными линиями. Анализ этих графиков показывает, что стабилизация кривых для моделей с двумя шарнирами наступила при значении k=0,8, с одним шарниром и одной жесткой заделкой при k=0,6, с двумя жесткими заделками при k=0,55. Таким образом, в первом случае необходимо использовать 16…17 нагелей, во втором - 13…14, в третьем - 12…13.
Способ динамического воздействия на модели. Динамические испытания моделей проводились в резонансном режиме. Частоты поперечных колебаний балок определялись с помощью электронного частотомера марки ЧЗ-63/1, который снимал показания с индукционного вибродатчика. Колебания возбуждались двигателем постоянного тока с дисбалансом массой примерно 15 г, жестко закрепленным на моделях в середине пролета. Частота вращения двигателя с дисбалансом регулировалась блоком питания постоянного тока с плавным регулированием силы тока. Момент наступления резонанса контролировался электронно-лучевым осциллографом марки C1-65A по максимальной амплитуде выходного сигнала с индукционного вибродатчика.
При динамических испытаниях были определены первые резонансные частоты колебаний, которые приведены в таблице (в колонке 4). По этим результатам построены графики ω-k, которые представлены на чертеже сплошными линиями. Анализ этих графиков показывает, что стабилизация кривых для рассмотренных моделей произошла при тех же соотношениях k, что и в первом случае.
Как видно из сравнения, результаты, полученные обоими способами, практически совпадают. Однако способ с использованием вибрационного метода менее трудоемкий, поскольку при его реализации отпадает операция статического нагружения модели.
Таким образом, технический результат - возможность определения оптимального количества нагелей в составных конструкциях достигается за счет использования моделей и испытания их в условиях статического и динамического нагружения при поэтапном увеличения числа нагелей до стабилизации контролируемых параметров.
Источники информации
1. Конструкции из дерева и пластмасс: Под редакцией Г.Г.Карлсена и др. [Текст] - М.: Стройиздат, 1986.
2. СНиП II-23-81*. Деревянные конструкции. Нормы проектирования [Текст]. - М.: Стройиздат, 1982. - 54 с.
3. Шаповалов Л.А. Моделирование в задачах механики элементов конструкций [Текст] / Л.А.Шаповалов. - М.: Машиностроение, 1990. - 287 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ИЗГИБНОЙ ЖЕСТКОСТИ УКРУПНИТЕЛЬНОГО СТЫКА ОДНОПРОЛЕТНЫХ СОСТАВНЫХ БАЛОК ПОСТОЯННОГО СЕЧЕНИЯ (ВАРИАНТЫ) | 2006 |
|
RU2306547C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНОГО ПРОГИБА ОДНОПРОЛЕТНЫХ СОСТАВНЫХ ДЕРЕВЯННЫХ БАЛОК С УКРУПНИТЕЛЬНЫМИ СТЫКАМИ | 2006 |
|
RU2308699C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНОГО ПРОГИБА КОНСТРУКЦИЙ В ВИДЕ УПРУГИХ БАЛОК И БАЛОЧНЫХ ПЛИТ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ НАГРУЗКОЙ | 2001 |
|
RU2213953C2 |
| СПОСОБ УЧЕТА СОВМЕСТНОСТИ РАБОТЫ ДВУХСЛОЙНЫХ ДЕРЕВЯННЫХ КОНСТРУКЦИЙ БАЛОЧНОГО ТИПА | 2004 |
|
RU2255317C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МАКСИМАЛЬНОГО ПЕРЕМЕЩЕНИЯ ЭЛЕМЕНТА КОНСТРУКЦИИ В ВИДЕ ПЛАСТИНКИ ПРИ ПОПЕРЕЧНОМ ИЗГИБЕ ПОД ДЕЙСТВИЕМ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ НАГРУЗКИ | 1999 |
|
RU2157520C1 |
| СПОСОБ КОНТРОЛЯ ЖЕСТКОСТИ ОДНОПРОЛЕТНЫХ БАЛОК ИЗ ФИЗИЧЕСКИ НЕЛИНЕЙНОГО МАТЕРИАЛА | 2013 |
|
RU2538361C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЖЕСТКОСТИ ГОРИЗОНТАЛЬНОГО ШВА В ДВУХСЛОЙНЫХ КОНСТРУКЦИЯХ БАЛОЧНОГО ТИПА | 2009 |
|
RU2406075C1 |
| СПОСОБ ИСПЫТАНИЙ УЗЛОВ ТРЕНИЯ | 2006 |
|
RU2343450C2 |
| Способ усталостных испытаний лопастей воздушного винта и установка для его осуществления | 2021 |
|
RU2767594C1 |
| СПОСОБ ИСПЫТАНИЯ ОБРАЗЦОВ ФАСАДНЫХ КОНСТРУКЦИЙ С ПРИЛОЖЕНИЕМ РАВНОМЕРНО РАСПРЕДЕЛЕННОЙ НАГРУЗКИ | 2022 |
|
RU2786782C1 |
Изобретение относится к области строительства и предназначено для определения оптимального числа нагелей в двухслойных деревянных конструкциях балочного типа. Технический результат - разработка способа экспериментального определения оптимального количества нагелей в составных балках с использованием их моделей. Способ определения оптимального количества нагелей в составной деревянной балке заключается в установке на ней минимально возможного количества нагелей, закреплении на испытательном стенде согласно условиям эксплуатации балки, нагружении ее равномерно распределенной нагрузкой, измерении максимального прогиба, разгрузке, установке дополнительных нагелей посредине между ранее установленными нагелями и повторении статических испытаний до момента стабилизации максимального прогиба. По результатам статических испытаний строят графическую зависимость «максимальный прогиб - отношение числа поставленных нагелей на каждом этапе испытаний к максимальному числу использованных нагелей», проводят анализ кривых и более точно определяют начало участка стабилизации максимального прогиба, по которому вычисляют оптимальное количество нагелей для рассматриваемой модели и соответственно натурной балки. Такого же результата можно достичь, если в способе определения оптимального количества нагелей вместо статических испытаний проводить динамические испытания балки на изгиб, возбуждая в ней поперечные собственные (или вынужденные) колебания и измеряя основную (или первую резонансную) частоту этих колебаний, поэтапно увеличивая число нагелей. 2 н.п. ф-лы, 1 ил.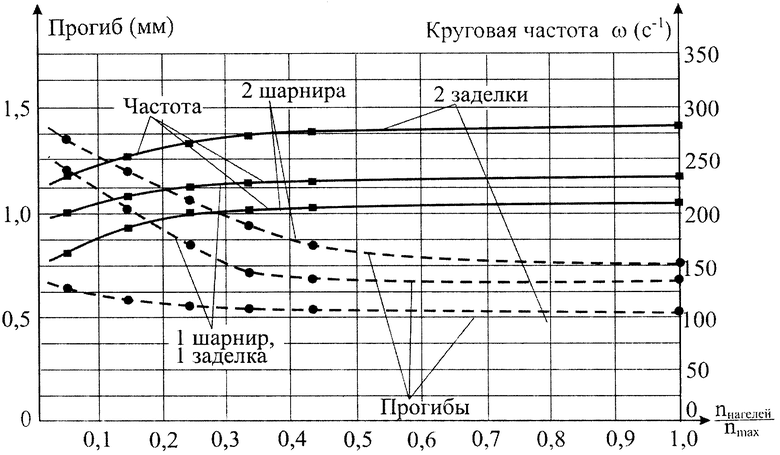
1. Способ определения оптимального количества нагелей в составной деревянной балке, заключающийся в изготовлении модели балки с соблюдением условий геометрического и физико-механического подобия, установке на ней минимально возможного количества нагелей, закреплении модели на испытательном стенде согласно условиям эксплуатации балки, нагружении ее равномерно распределенной нагрузкой, равной по условиям физического подобия расчетной, измерении максимального прогиба, разгружении модели, постановке дополнительных нагелей посредине между уже ранее установленными нагелями, повторении операций нагружения, измерения и разгружения и выполнении всего цикла статических испытаний при поэтапном увеличении количества нагелей до стабилизации измеряемой величины максимального прогиба; далее по результатам статических испытаний строят графическую зависимость «максимальный прогиб - отношение числа поставленных нагелей на каждом этапе испытаний к максимальному числу использованных нагелей», проводят анализ кривых и более точно определяют начало участка стабилизации максимального прогиба, по которому вычисляют оптимальное количество нагелей для рассматриваемой модели и соответственно натурной балки.
2. Способ определения оптимального количества нагелей в составной деревянной балке, заключающийся в изготовлении модели балки с соблюдением условий геометрического и физико-механического подобия, постановке минимально возможного количества нагелей, установке и закреплении модели на испытательном стенде согласно условиям эксплуатации балки, возбуждении в модели поперечных собственных или вынужденных колебаний, измерении основной (или первой резонансной) частоты колебаний, постановке дополнительных нагелей посредине между ранее установленными нагелями, повторении операций возбуждения колебаний и измерения их частоты и далее выполнении всего цикла динамических испытаний при поэтапном увеличении количества нагелей до стабилизации измеряемой величины основной (или первой резонансной) частоты колебаний; затем по результатам динамических испытаний строят графическую зависимость «основная (или первая резонансная) частота колебаний - отношение числа поставленных нагелей на каждом этапе испытаний к максимальному числу нагелей», проводят анализ кривых и более точно определяют начало участка стабилизации частоты колебаний, по которой вычисляют оптимальное количество нагелей для рассматриваемой модели и соответственно натурной балки.
| Конструкции из дерева и пластмасс | |||
| / Под редакцией Г.Г.Карлсена и др | |||
| [Текст] - М.: Стройиздат, 1986 | |||
| Прибор для равномерного смешения зерна и одновременного отбирания нескольких одинаковых по объему проб | 1921 |
|
SU23A1 |
| Деревянные конструкции | |||
| Нормы проектирования [Текст] | |||
| - М.: Стройиздат, 1982, - 54 с | |||
| СТО 36554501-002-2006 «Деревянные клееные конструкции | |||
| Методы расчета» | |||
| Пломбировальные щипцы | 1923 |
|
SU2006A1 |
Авторы
Даты
2011-12-10—Публикация
2009-12-21—Подача