Изобретение относится к горному и строительному делу и может использоваться при определении контактных условий вида "полное сцепление" и "полное проскальзывание" в сопряжении соосных цилиндрических поверхностей совместно деформирующихся элементов составной системы, например, при измерениях параметров напряженно-деформированного состояния горных пород и массивных строительных конструкций с использованием скважинных упругих датчиков, а также при оценке контактных условий в технических системах, содержащих соосные цилиндрические элементы.
Известны способы оценки напряжений в горных породах и массивных строительных конструкциях (например, в бетонных плотинах, в бетонной и каменной крепи тоннелей, в фундаментах строительных конструкций и т.п.) с использованием упругих скважинных датчиков, например, кольцевых фотоупругих датчиков (авт.св. СССР N 342049, G 01 B 11/18, E 21 C 39/00, опубл. в БИ N 19 за 1972 г.) - далее КФ-датчиков. Последний представляет собой в общем случае многослойное кольцо из различных оптически чувствительных материалов. В дальнейшем рассматривается в качестве КФ-датчика напряжений только внутреннее кольцо, изготовленное, например, из силикатного стекла, то есть простейший случай - однослойный КФ-датчик.
Способ измерения напряжений с использованием КФ-датчика заключается в следующем: в породе из горной выработки бурят скважину, в которой устанавливают КФ-датчик. Зазор между боковой цилиндрической поверхностью КФ-датчика и стенками скважины заполняют самотвердеющим клеем, например, цементным раствором. После затвердевания клея КФ-датчик деформируется совместно со стенками скважины и окружающей средой (породой, бетоном и т.п.). При этом в КФ-датчике возникают напряжения, пропорциональные изменению напряженно-деформированного состояния этой среды. При освещении КФ-датчика лучем поляризованного света и наблюдении с помощью полярископа в нем формируется оптическая картина, по структуре (узору) которой судят о приросте напряжений в КФ-датчике и окружающей среде, о величине, ориентации и соотношении квазиглавных напряжений в среде, действующих в плоскости, ортогональной к оси скважины и КФ-датчика.
Однако при известном способе не учитывают контактные условия на сопряжении цилиндрических поверхностей КФ-датчика и скважины, что может приводить к значительным погрешностям при измерениях.
Известен способ расшифровки показаний КФ-датчика (Влох Н.П., Сашурин А. Д. Измерение напряжений в массиве крепких горных пород. - М.: Недра, 1970, с. 69-80). Методику расшифровки показаний КФ-датчика в этом способе строят на основе решения задачи теории упругости о совместном деформировании КФ-датчика и стенок скважины. В качестве условий сопряжения на контакте КФ-датчика и стенок скважины принято условие "полное сцепление" (там же, с. 7, формулы 54-55). При этом принятое контактное условие не обосновывают ни теоретически, ни экспериментально.
В работе (Hawkes J. , Fellers G.E. Theory of the Determination of the Greatest Principal stress in a Biaxial stress Field Using Photoelastic Hollow Cylinder Inclussions // Int. J. Rock Mech. Min. Sci. 1969. V. 6. p. 143-158) рассмотрена аналогичная задача применительно к КФ-датчику, устанавливаемому в скважине. В качестве условия сопряжения авторами этой работы также принято условие "полное сцепление" без экспериментального или теоретического обоснования.
Применительно к КФ-датчикам при теоретическом рассмотрении их работы в скважинах контактное условие вида "полное сцепление" рассматривалось также в других работах (Hiramatsu Y., Niva Y., Oka Y. Measurement stress in the Field by Application of Photoelasticity // Tech. Rept Eng-ng Res. Inst. Kyoto Univ. 1957. V. VII. 3. N 37; Сенук Д.П. Измерение напряжений в породах месторождений Севера. - Новосибирск: Наука, 1983, с. 28,53).
Контактное условие вида "полное проскальзывание" в перечисленных работах не рассматривалось. Какие-либо пояснения по этому вопросу в указанных работах не приведены.
Итак, при известных способах использования КФ-датчиков не учитывают конкретный вид контактных условий на сопряжении КФ-датчика с клеем и стенками скважины, а при расчетах принимают условие "полное сцепление". Это может приводить к значительным погрешностям при расшифровке показаний таких КФ-датчиков.
Насколько известно авторам заявляемого технического решения, способы определения конкретного вида контактных условий отсутствуют. Предлагаемый способ определения контактных условий вида "полное сцепление" и "полное проскальзывание" на основе особенностей в структуре изохром оптической картины в КФ-датчиках следует отнести к предлагаемому впервые техническому решению. Оно основано на применении КФ-датчика по новому назначению - в качестве устройства для определения неизмеряемой ранее физической величины - вида контактных условий.
Предлагаемый способ решает следующую техническую задачу: позволяет измерять ранее не измеряемую физическую величину - контактные условия вида "полное сцепление" и "полное проскальзывание" применительно к составным системам, содержащим цилиндрический элемент, установленный в цилиндрической полости в породе, которые совместно деформируются при приложении внешних сил к рассматриваемой системе и распределение напряжений в которых после деформирования оказывается разным, в зависимости от конкретного вида контактных условий на границе контакта между цилиндрическим элементом и цилиндрической полостью. Это достигается за счет моделирования цилиндрического элемента КФ-датчиком и последующего исследования структуры оптической картины в нем.
Поставленная задача решается тем, что предлагается способ определения контактных условий вида "полное сцепление" и "полное проскальзывание" в сопряжении соосных цилиндрических поверхностей совместно деформирующихся элементов составной системы, состоящей из среды (породы), цилиндрической полости (скважины) в породе и соосного с ней цилиндрического элемента, заключающийся в том, что цилиндрический элемент этой системы моделируют КФ-датчиком, при этом предварительно решают расчетным путем контактные задачи теории упругости, определяя максимальные касательные напряжения τmax в КФ-датчике при контактных условиях в сопряжении, соответствующих "полному сцеплению" и "полному проскальзыванию". Затем по результатам решения строят эталонные картины изолиний τmax для каждого вида контактных условий в сопряжении при разных параметрах λ напряженного состояния породы:
-1 ≤ (λ = p/q) ≤ 1, (1)
где p и q - соответственно минимальное и максимальное квазиглавные напряжения в среде (породе) составной системы в плоскости, нормальной оси КФ-датчика.
Далее в поляризованном свете наблюдают оптическую картину изохром в КФ-датчике, размещенном в цилиндрической полости составной системы, после чего сравнивают структуру наблюдаемой оптической картины изохром в этом датчике со структурой построенных эталонных картин изолиний τmax и по результатам сравнения определяют искомый вид контактных условий в сопряжении, за который принимают тот, при котором особенности структуры наблюдаемой оптической картины изохром в КФ-датчике в наибольшей степени совпадают с особенностями структуры эталонной картины изолиний τmax.
КФ-датчик напряжений используют в качестве устройства для определения контактных условий вида "полное сцепление" и "полное проскальзывание" в сопряжении соосных цилиндрических поверхностей совместно деформирующихся элементов составной системы.
Указанная совокупность признаков позволяет решить сформулированную техническую задачу.
Способ реализован применительно к составным системам твердых тел, содержащим взаимно деформирующиеся соосные цилиндрические элементы, например, в виде совокупности скважины, пробуренной в породе, и цилиндрического элемента в виде КФ-датчика, например, из стекла, размещенного в скважине, полагая, что зазор между стенками скважины и КФ-датчиком заполнен самотвердеющим клеем, толщину которого условно принимают равной нулю.
При любом деформировании породного массива, в котором пробурена скважина, КФ-датчик будет деформироваться совместно со стенками скважины и прилегающей породой. В процессе их взаимного деформирования на контакте стенок скважины и цилиндрической боковой поверхности КФ-датчика возникает взаимодействие, которое в механике твердого деформируемого тела характеризуется контактными условиями (условиями сопряжения). Известны и рассматриваются два вида такого сопряжения - "полное сцепление" и "полное проскальзывание", каждое из которых задается своей совокупностью соотношений напряжений на контактирующих поверхностях и описывает кинематику взаимного перемещения этих поверхностей, то есть выступает в роли самостоятельной физической величины.
Чтобы выявить особенности распределения напряжений в цилиндрическом элементе, последний моделируют КФ-датчиком, который размещают в скважине вместо цилиндрического элемента, производят силовое воздействие на систему и следят с помощью луча поляризованного света за оптической картиной в КФ-датчике.
В качестве способа силового воздействия на составную систему из скважины с размещенным в ней КФ-датчиком и прилегающей к стенкам скважины породы выполняют обуривание скважины с КФ-датчиком кольцевой щелью. При этом в обуренном керне произойдут деформации восстановления, что приведет к появлению напряжений в КФ-датчике, поскольку последний склеен со стенками скважины.
Чтобы по структуре возникшей в КФ-датчике оптической картины изохром судить о конкретном виде контактных условий, предварительно строят эталонные картины изолиний максимальных касательных напряжений τmax в КФ-датчике для случаев "полное сцепление" и "полное проскальзывание", учитывая, что согласно законам фотоупругости структура изохром оптической картины совпадает со структурой изолиний τmax в фотоупругом элементе.
Для построения эталонных картин τmax в КФ-датчике предварительно решают соответствующие контактные задачи теории упругости. При двух видах контактных условий необходимо применительно к КФ-датчику решить две задачи для случая "полное сцепление" и для случая "полное проскальзывание". На основе теоретического решения рассчитывают и строят поля изолиний τmax поперечном сечении КФ-датчика.
Вследствие того, что в процессе деформирования составной системы, содержащей соосные цилиндрические элементы, при силовом воздействии на составную систему распределение исходных напряжений в породе может быть произвольным, необходимо учитывать это обстоятельство. Распределение исходных напряжений в породе вокруг скважины с КФ-датчиком можно характеризовать квазиглавными напряжениями p и q, действующими в плоскости, нормальной оси скважины с КФ-датчиком. Полагая |p| ≤ |q|, исходное напряженное состояние породы обычно характеризуют относительным безразмерным параметром λ = p/q. Величины p и q могут быть растягивающими (q > 0, p > 0) и сжимающими (q < 0, p < 0), соответственно параметр λ может принимать значения в диапазоне -1 ≤ λ ≤ 1 (λ = 1 при p = q, λ =-1 при |p| = |q|, p < 0, q > 0, либо при p > 0, q < 0).
Учитывая, что λ принимает различные значения, набор эталонных картин изолиний τmax необходимо иметь при различных значениях λ. Выбор шага по λ определяется необходимой точностью планируемых измерений.
После установки КФ-датчика в скважине и обуривания его кольцевой щелью наблюдают в нем оптическую картину с помощью полярископа (например, типа ПШ-2), фиксируя структуру изохром (оптическую картину либо зарисовывают, либо фотографируют). Затем наблюдаемую оптическую картину изохром в этом датчике сравнивают с набором эталонных картин τmax. За искомый вид контактных условий принимают тот, при котором особенности структуры наблюдаемой оптической картины изохром в КФ-датчике в наибольшей степени совпадают с особенностями структуры эталонных картин τmax.
Целесообразно при реализации способа использовать КФ-датчик, состоящий из оптически чувствительной и металлической частей, в котором металлическая часть выполнена из того же материала, что и цилиндрический элемент составной системы (например, по авт. св. СССР N 724732, E 21 C 39/00 опубл. в БИ N 12 за 1980 г.). Это позволяет расширить область использования способа на составные системы, содержащие цилиндрические элементы из различных материалов, включая металлические.
Сущность предлагаемого технического решения поясняется чертежами, таблицей и примерами конкретности исполнения.
На фиг. 1-5 приведены эталонные картины изолиний τmax в КФ-датчике, построенные расчетным путем с использованием теоретического решения контактной задачи теории упругости о полной разгрузке керна с центральной скважиной и установленным в ней КФ-датчиком, работающим в условиях "полное проскальзывание" по боковой цилиндрической поверхности КФ-датчика со стенками скважины:
фиг. 1 - изолинии τmax в КФ-датчике при p = 0, q = 1 МПа, λ = 0;
фиг. 2 - то же при p = 0,25 МПа, q = 1 МПа, λ = 0,25;
фиг. 3 - то же при p = 0,5 МПа, q = 1 МПа, λ = 0,5;
фиг. 4 - то же при p = 0,75 МПа, q = 1 МПа, λ = 0,75;
фиг. 5 - то же при p = 1 МПа, q = 1 МПа, λ = 1.
Нф фиг. 6-10 приведены эталонные картины изолиний τmax в КФ-датчике, построенные расчетным путем с использованием теоретического решения контактной задачи теории упругости о полной разгрузке керна с центральной скважиной и установленным в ней КФ-датчиком, работающим в условиях "полное сцепление" по боковой цилиндрической поверхности КФ-датчика со стенками скважины при тех же параметрах системы, что и в задаче о "полном проскальзывании":
фиг. 6 - изолинии τmax в КФ-датчике в условиях "полное сцепление" при p = 0, q = 1 МПа, λ = 0;
фиг. 7 - то же при p = 0,25 МПа, q = 1 МПа, λ = 0,25;
фиг. 8 - то же при p = 0,5 МПа, q = 1 МПа, λ = 0,5;
фиг. 9 - то же при p = 0,75 МПа, q = 1 МПа, λ = 0,75;
фиг. 10 - то же при p = 1 МПа, q = 1 МПа, λ = 1.
На фиг. 1 стрелками указаны направления квазиглавных напряжений p и q в породе. Аналогичная ориентация p и q принята на остальных фигурах.
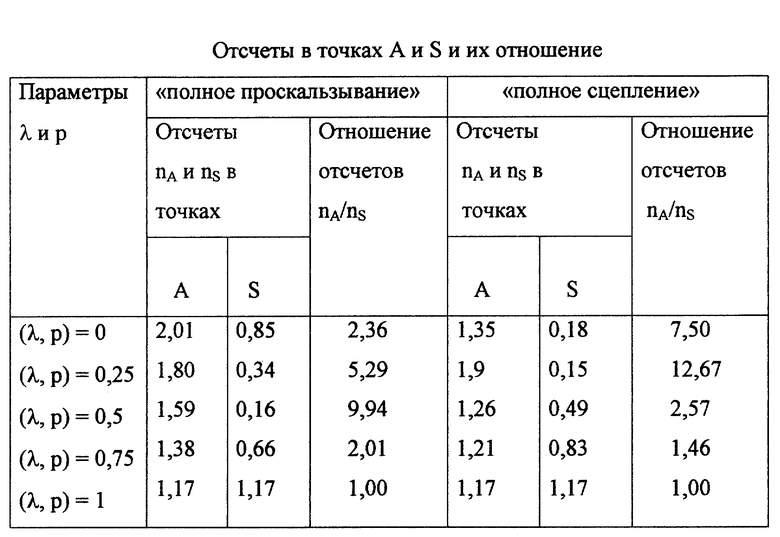
В таблице приведены величины отсчетов в точках A и S (фиг. 1). За точки A приняты точки на внутреннем контуре КФ-датчика на пересечении с горизонтальным диаметром на фиг. 1 - фиг. 10, совпадающим с направлением минимального квазиглавного напряжения p в породе. За точки S приняты точки пересечения внутреннего контура КФ-датчика с вертикальным диаметром на тех же фигурах, совпадающим с ориентацией максимального квазиглавного напряжения q в породе.
Предлагаемый способ реализуют следующим образом.
В качестве цилиндрического элемента составной системы используют КФ-датчик напряжений, в качестве цилиндрической полости - скважину, в качестве совместно деформирующихся элементов составной системы - КФ-датчик, скважину и в качестве окружающей среды - массив горных пород вокруг скважины с КФ-датчиком.
Предварительно расчетным путем решают контактные задачи теории упругости для построения эталонных картин изолиний τmax.
Первый пример реализации способа.
Рассмотрим случай полной разгрузки керна с центральной скважиной и установленным в ней КФ-датчиком. Разгрузку осуществляют бурением кольцевой разгрузочной щели.
Задача для случая контактных условий вида "полное проскальзывание" на контакте КФ-датчика со стенками скважины (в полярных координатах при r = R):
условие "полное проскальзывание":
где r - полярный радиус (координата);
R - внешний радиус КФ-датчика;
σr1,σr - соответственно радиальные напряжения в КФ-датчике и породе;
τrθ1,τrθ - соответственно касательные напряжения в КФ-датчике и породе;
ur1, ur - радиальные перемещения в КФ-датчике и породе.
В задаче также должны выполняться:
- условия на бесконечности: σχ = p, σγ = q,
- граничные условия на контуре внутреннего отверстия КФ-датчика радиуса R1 (при r = R1): σr1 = 0; τrθ1 = 0,
где R1 - радиус внутреннего отверстия КФ-датчика;
σχ,σγ - напряжения в породе в декартовой системе координат χ и γ;
- условия на контуре кольцевой разгрузочной щели внутреннего радиуса R2 (r = R2):
σr2= -σr;τrθ2 = -τrθ,
где σr2,τrθ2 - соответственно радиальное и касательное напряжения на контуре кольцевой разгрузочной щели в породе.
Задача решается при условии, что толщина слоя клея между КФ-датчиком и стенками скважины равна нулю, а КФ-датчик установлен вдали от дна скважины. При решении задачи приняты численные значения параметров системы: КФ-датчик из стекла марки К8, модуль упругости которого Eд = 6,3 • 104 МПа, коэффициент Пуассона νд= 0,21, внешний радиус КФ-датчика R = 1,8 см, внутренний радиус R1 = 0,3 см, модуль упругости породы Eп = 1,575 • 104 МПа, коэффициент Пуассона νп= 0,25. Радиус кольцевой разгрузочной щели R2 = 5,6 см. Методика решения сформулированной контактной задачи приведена, например, в монографии: Г. Н. Савин. Механика твердого деформируемого тела. Избранные труды. - Киев: "Наукова Думка", 1979, с. 89, 93.
Пусть по каким-либо причинам в реальной ситуации условие (2) применительно к КФ-датчику, установленному в скважине, не выполняется. Теоретически решают ту же задачу с использованием контактных условий вида "полное сцепление" при r = R.
Условие "полное сцепление":
где υθ1,υθ - соответственно тангенциальные перемещения в КФ-датчике и породе.
Остальные обозначения, что и в формулах (2).
Полученные решения сформулированных задач используют для построения расчетным путем или на компьютере эталонных картин τmax в поперечном сечении КФ-датчика с использованием условия (2) - фиг. 1 - 5 и условия (3) - фиг. 6-10.
Различные виды контактных условий (или условий сопряжения) рассматриваются в контактных задачах теории упругости и механики твердого деформируемого тела (см., например, монографию: Г.Н. Савин. Механика твердого деформируемого тела. Избранные труды. - Киев: "Наукова Думка", - 1979, с. 83, 89, 93). Условие "полное сцепление", аналогичное вышеприведенным соотношениям (3), рассмотрены на с. 83 названной монографии. Условие "полное проскальзывание", аналогичное соотношениям (2), рассмотрено на с. 89, 93.
Условия (2) и (3) позволяют уточнить, что понимается в настоящей заявке на предлагаемое изобретение под терминами: физическая величина - контактные условия вида "полное проскальзывание" и физическая величина - контактные условия вида "полное сцепление".
Это физическая величина, принимающая два разных вида: "полное сцепление" и "полное проскальзывание":
"полное проскальзывание" характеризуется совокупностью четырех условий (2), которые должны одновременно выполняться;
"полное сцепление" характеризуется совокупностью четырех условий (3), которые также должны одновременно выполняться.
Два вида рассматриваемой физической величины физически характеризуют два случая возможного механического состояния материала на сопрягающихся поверхностях взаимно деформирующихся элементов составной системы.
Рассмотрим картины изолиний при λ = 0 при "полном проскальзывании" (фиг. 1) и "полном сцеплении" (фиг. 6). Из структуры картины изолиний τmax на этих фигурах видно, что они (структуры изолиний τmax, а значит, и структуры изохром на соответствующих оптических картинах) существенно различаются. Заметим, что в этом случае обе системы физически совершенно одинаковы и отличаются только видом контактных условий.
Такое же различие в структуре изолиний τmax наблюдается на фиг. 2 и фиг. 7 при p = 0,25 (λ = 0,25). То же относится к структуре изолиний τmax при p = 0,5 (λ = 0,5) на фиг. 3 и на фиг. 8. То же относится к структуре изолиний τmax при p = 0,75 (λ = 0,75) на фиг. 4 и на фиг. 9.
И только при p = 1 (λ = 1) структура изолиний τmax в КФ-датчиках при обоих видах контактных условий одинакова (см. фиг. 5 и фиг. 10) - представлена концентрическими окружностями в обоих случаях.
Таким образом, анализ структуры изолиний τmax в КФ-датчиках в случае полной разгрузки керна с центральной скважиной и установленным в ней КФ-датчиком в условиях "полное проскальзывание" (2) и "полное сцепление" (3) показывает, что они по структуре различны. Следовательно, не возникает затруднений обнаружить это различие в оптических картинах изохром в КФ-датчиках в процессе экспериментов.
Помимо различий в структуре изолиний τmax и в структуре изохром оптической картины имеет место различие в отсчетах в фиксированных точках этих картин (см. таблицу).
Величины отсчетов в точках A и S в таблице приведены согласно эталонным картинам изолиний τmax. Соответствующие отсчеты по оптической картине в КФ-датчиках можно получить, наблюдая оптическую картину с помощью полярископа с компенсатором. Величины отсчетов по КФ-датчикам в напряжениях можно получить, тарируя КФ-датчики в породных или бетонных кубиках, напряжения в которых задаются равными значениям p и q, для которых построены эталонные картины изолиний τmax на фиг. 1-10. Очевидно, отсчеты по оптической картине в КФ-датчиках будут пропорциональны отсчетам nA и ns по эталонным картинам изолиний τmax. Соответствующие коэффициенты пропорциональности могут быть получены в процессе тарирования КФ-датчиков.
Из таблицы следует, что отсчеты в фиксированных точках эталонных картин изолинии τmax различны в случаях "полное сцепление" и "полное проскальзывание", за исключением случая λ = 1,0. Отношение отсчетов в точках A и S также различно в рассматриваемых случаях.
Из изложенного следует, что различие в оптических картинах в КФ-датчике в случаях "полное сцепление" и "полное проскальзывание" может быть установлено не только путем визуальных наблюдений, но и с использованием приборов для снятия отсчетов по фиксированным точкам оптической картины.
Используя данные, приведенные в таблице, можно по отношению отсчетов в точках A и S оптической картины оценить вид контактных условий. Последнее, очевидно, справедливо и для любых других точек отсчета на оптической картине.
После анализа теоретических картин изолиний τmax в КФ-датчиках и построения набора эталонных картин изолиний τmax для случаев "полное проскальзывание" (фиг. 1-5) и "полное сцепление" (фиг. 6-10) приступают к выполнению натурных измерений. Для этого в подземной горной выработке бурят скважину диаметром 48 мм (при использовании КФ-датчиков диаметром 46 мм). В скважине устанавливают КФ-датчик, зазор между ним и стенками скважины заполняют самотвердеющим клеем - например, цементным раствором. После затвердевания клея по КФ-датчику производят контрольный отсчет с помощью полярископа, например, типа ПШ-2 - наблюдают оптическую картину и зарисовывают или фотографируют ее, затем снимают отсчеты в фиксированных точках оптической картины, например, в точках A и S. Начальный отсчет в этом случае нулевой (оптической картины нет, так как система за время затвердевания клея не испытывала пригрузок). Далее с использованием бурового станка и кольцевой коронки диаметром 112 мм вокруг скважины с КФ-датчиком обуривают кольцевую щель на глубину 10-15 см за место установки КФ-датчика, чтобы обеспечить полную разгрузку керна. Вследствие деформаций восстановления керна в КФ-датчике возникают напряжения. Затем с помощью полярископа наблюдают в КФ-датчике сформировавшуюся оптическую картину. Структуру изохром этой картины тщательно сравнивают со структурами изолиний τmax на эталонных картинах (фиг. 1-10). Из 10 эталонных картин изолиний τmax выбирают одну, структура изолиний τmax которой более всего соответствует структуре изохром оптической картины в КФ-датчике после разгрузки керна с КФ-датчиком.
Второй пример реализации способа.
Пусть имеем штанговую (анкерную) крепь горной выработки - в этом случае в качестве крепи используют металлические штанги, которые устанавливают в скважине, пробуренной в горной породе, например, в кровле выработки, зазор между металлической штангой и стенками скважины заполняют эпоксидным компаундом или цементным раствором. Поставим задачу - определить контактные условия в системе металлическая штанга - скважина - горная порода.
При решении этой задачи заменяют металлическую штангу диаметром 46 мм моделью в виде КФ-датчика. Для этого внешний конец штанги, расположенный на глубине 0,3-1,0 м от устья скважины, оформляют в виде плоской отшлифованной поверхности. В центре ее торца просверливают осевое отверстие диаметром 7 мм. На торец наклеивают кольцевое фотоупругое покрытие в форме диска из оптически чувствительного материала (например, полистирола типа СД-5). Штанга с фотоупругим кольцевым покрытием будет моделировать КФ-датчик (аналогичный КФ-датчик рассмотрен в а.с. СССР N 724732, E 21 C 39/00, опубл. в БИ N 12 за 1980 г.).
Такой КФ-датчик состоит из металлического цилиндрического элемента с осевым отверстием малого диаметра и кольцевого
фотоупругого покрытия, наклеенного на торец металлического кольцевого цилиндра. Применительно к такому КФ-датчику будут справедливы рассмотренные выше две задачи с контактными условиями вида "полное сцепление" и "полное проскальзывание". Если геометрические размеры КФ-датчика со стеклянным оптически чувствительным элементом совпадают с геометрическими размерами (внешний радиус и радиус осевого отверстия) металлического КФ- датчика (с фотоупругим покрытием), то эталонные картины изолиний максимальных касательных напряжений τmax в металлическом КФ-датчике также будут иметь вид, аналогичный приведенным на фиг. 1-10.
Затем к системе из модели КФ-датчика, скважины и горной породы прилагают внешнюю нагрузку, например, путем обуривания кольцевой щелью. Далее наблюдают оптическую картину в фотоупругом покрытии с помощью полярископа. Сравнивают структуру изохром оптической картины в фотоупругом покрытии металлического КФ-датчика с набором эталонных картин изолиний τmax и по наиболее близко подходящей эталонной картине изолиний τmax оценивают вид контактных условий.
Если геометрические размеры металлического цилиндра (цилиндр может быть и из других материалов - сплавов, компаундов и т.п.) - внешний и внутренний радиусы - отличны и резко отличаются модули упругости модели металлического датчика и стеклянного датчика, то эталонные картины рассчитывают и строят каждый раз заново.
Для определения вида контактных условий на сопряжении боковой поверхности штанги и стенок скважины вместо специально оформленной штанги можно использовать в качестве ее модели КФ-датчик, кольцевой цилиндр которого выполнен из металла, а на торец нанесено фотоупругое покрытие. При этом цилиндрический элемент должен быть из того же материала, из которого изготовлена штанга, моделью которой будет КФ-датчик. Для заполнения зазора между КФ-датчиком и стенками скважины необходимо использовать тот состав клея, который используют при установке штанг.
Сущность применения известного устройства - КФ-датчика по новому назначению - для определения контактных условий вида "полное сцепление" и "полное проскальзывание" - заключается в следующем.
КФ-датчик, например, по а.с. СССР N 342049, E 21 C 39/00, опубл. в БИ N 19, 1972 г. , предназначен для измерения механических напряжений в горных породах, бетонах и т.п. и выполнен в виде нескольких коаксиально расположенных колец из различных оптически чувствительных (активных) материалов, задняя торцевая поверхность которых снабжена зеркальным слоем. Частными случаями КФ-датчика будут: двухслойный КФ-датчик (состоящий из двух колец, вставленных одно в другое соосно) и однослойный КФ-датчик. Такой КФ-датчик устанавливают в скважине, пробуренной в горной породе, приклеивают по цилиндрической поверхности к стенкам скважины и он совместно деформируется со стенками скважины и окружающей породой при любом изменении напряженно-деформированного состояния породы, произошедшего после установки КФ-датчика в скважине.
При наблюдении такого КФ-датчика в поляризованном свете (например, с помощью шахтного полярископа типа ПШ-2) в нем формируется оптическая картина, по структуре которой судят о приросте квазиглавных напряжений в породе в плоскости, ортогональной оси КФ-датчика (по порядку изохромы в фиксированной точке оптической картины), а направления (ориентацию) этих квазиглавных напряжений определяют по ориентации осей симметрии оптической картины, из которых одна ось совпадает с ориентацией максимального квазиглавного напряжения q в породе, а вторая ось совпадает с направлением минимального квазиглавного напряжения p в породе.
Еще одной разновидностью КФ-датчика является устройство по а. с. СССР N 724732. Оно состоит из металлического цилиндра с осевым отверстием и кольцевого фотоупругого покрытия. Металлический цилиндр выполнен из двух склеенных между собой полуцилиндров из разных материалов. Различие в модулях упругости последних позволяет дополнительно судить о величине модуля упругости породы, в которой установлен такой КФ-датчик. Если полуцилиндры выполнены из одного и того же материала, КФ-датчик используют для измерения напряжений. Структура оптической картины в датчике зависит от контактных условий на контакте между датчиком и стенками скважины (при малой толщине слоя клея его можно принять равным нулю при теоретических расчетах).
Виды контактных условий ранее не рассматривались в виде самостоятельной физической величины и экспериментально не измерялись. Фиг. 1-10 подтверждают, что КФ-датчики могут использоваться для оценки вида контактных условий.
Использование КФ-датчика в качестве датчика вида контактных условий иллюстрируется описанным выше способом определения вида контактных условий.
Предлагаемое техническое решение по определению вида контактных условий в системах, содержащих соосные цилиндрические элементы, позволит более точно проводить измерения напряжений и деформаций с использованием цилиндрических КФ-датчиков. Оно также позволит при выполнении теоретических расчетов напряжений в цилиндрических элементах предварительно экспериментально определять вид контактных условий в конкретной ситуации, который и использовать в теоретических расчетах.









Изобретение относится к горному и строительному делу и может использоваться при измерениях параметров напряженно-деформированного состояния горных пород и массивных строительных конструкций с использованием скважинных упругих датчиков, а также при оценке контактных условий в технических системах, содержащих соосные цилиндрические элементы. Способ определения контактных условий вида "полное сцепление" или "полное проскальзывание" в сопряжении соосных цилиндрических поверхностей совместно деформирующихся элементов составной системы, состоящей из среды (породы), цилиндрической полости - скважины в породе и соосного с ней цилиндрического элемента, заключается в том, что цилиндрический элемент этой системы моделируют КФ-датчиком. Предварительно решают расчетным путем контактные задачи теории упругости, определяя максимальные касательные напряжения τmax в КФ-датчике при контактных условиях в сопряжении, соответствующих "полному сцеплению" и "полному проскальзыванию". Затем по результатам решения строят эталонные картины изолиний τmax для каждого вида контактных условий в сопряжении при разных параметрах λ напряженного состояния породы: -1≤(λ=р/q)≤1, где р, q - соответственно минимальное и максимальное квазиглавные напряжения в среде (породе) составной системы в плоскости, нормальной оси КФ-датчика. Затем в поляризованном свете наблюдают оптическую картину изохром в КФ-датчике, размещенном в цилиндрической полости составной системы, после чего сравнивают структуру наблюдаемой оптической картины изохром в этом датчике со структурой построенных эталонных картин изолиний τmax и по результатам сравнения определяют искомый вид контактных условий в сопряжении, за который принимают тот, при котором особенности структуры наблюдаемой оптической картины изохром в КФ-датчике в наибольшей степени совпадают с особенностями структуры эталонной картины изолиний τmax. Технический результат: способ позволяет измерять ранее не измеряемую физическую величину - контактные условия вида "полное сцепление" и "полное проскальзывание" применительно к составным системам, которые совместно деформируются при приложении внешних сил и распределение напряжений в которых после деформирования оказывается разным, в зависимости от конкретного вида контактных условий на границе контакта между цилиндрическим элементом и цилиндрической полостью. 1 з.п.ф-лы, 10 ил. , 1 табл.
-1≤(λ=р/q)≤1,
где р, q - соответственно минимальное и максимальное квазиглавные напряжения материала среды, включающей цилиндрическую полость, в плоскости, нормальной оси этой полости и соосного с ней кольцевого фотоупругого датчика напряжений, затем в поляризованном свете наблюдают оптическую картину изохром в кольцевом фотоупругом датчике напряжений, размещенном в цилиндрической полости составной системы, после чего сравнивают структуру наблюдаемой оптической картины изохром в этом датчике со структурой построенных эталонных картин изолиний τmax и по результатам сравнения определяют искомый вид контактных условий в сопряжении, за который принимают тот, при котором особенности структуры наблюдаемой оптической картины изохром в кольцевом фотоупругом датчике напряжений, моделирующем цилиндрический элемент, в наибольшей степени совпадают с особенностями структуры эталонной картины изолиний τmax при фактическом параметре λ.
| ФОТОУПРУГИЙ ДАТЧИК НАПРЯЖЕНИЙ | 0 |
|
SU342049A1 |
| Фотоупругий датчик | 1973 |
|
SU533730A1 |
| ДАТЧИК ДЛЯ ИЗМЕРЕНИЯ ДЕФОРМАЦИЙ | 1991 |
|
RU2025658C1 |
| RU 95109996 А1, 20.05.1997 | |||
| СПОСОБ ИССЛЕДОВАНИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ ОБЪЕМНЫХ МОДЕЛЕЙ МАССИВА ГОРНЫХ ПОРОД | 1991 |
|
RU2053362C1 |
Авторы
Даты
2001-12-20—Публикация
1999-11-26—Подача