Изобретение относится к средствам и способам обучения, а именно обучению математике в школе. Может быть использовано при любом обучающем процессе, когда требуются концентрация внимания на отдельных элементах изучаемого материала, создание оптимальных условий для аналитической деятельности, а также при приобретении практических навыков выполнения пошаговых операций тех или иных изучаемых действий.
Эффективность процесса обучения в значительной степени определяется средствами и способами обучения, а также индивидуальными способностями учащихся. Известны средства обучения в виде различных опорных схем и блок-схем, таблиц с графами и строками, заполняемыми в процессе выполнения упражнений, примеров, задач. Причем последние, которые включают правила, программы действий, алгоритмы, и служат пособием для облегчения процесса освоения и запоминания изучаемой темы [1, 2]. Существенным недостатком этих средств является то, что они относятся к средствам, лишь помогающим воспроизводить знания и оказывающим определенную помощь в приобретении навыков, выполняя функции справочного материала. Кроме этого составляются они в системе символов, принятых в изучаемой теме в виде формул, чертежей, рисунков, что требует от учащихся значительных усилий по запоминанию и определенной подготовки для использования.
Известен способ обучения учащихся с составлением схем "Опорно-логической структуры раздела", включающий в логической последовательности теоретические основы раздела. По мере изучения раздела производят заполнение таблицы "Освоение раздела курса", куда заносятся сведения, величины и их производные в соответствии с схемами разделов.
Обучение ведется поэтапно с последовательным составлением схемы раздела и заполнением таблицы с проработкой соответствующих задач. Алгоритмичность обеспечивается за счет логического построения схемы и перенесения логической последовательности в таблицу [3]. Недостатком этого способа является то, что схемы и таблицы выполняют функцию справочного пособия, лишь облегчая усилия по приобретению навыков, не способствуют запоминанию логических структур, так как включают большой объем информации целого раздела. Кроме этого логическая структура может обеспечить осмысливание той или иной программы действия, алгоритма лишь отчасти и то у наиболее развитых учащихся, умеющих развернуть представленные сведения в пошаговую программу действий, что ограничивает применение таблиц для приобретения навыков выполнения действий, решения задач.
Средства для обучения с использованием алгоритмического компонента используются при традиционных способах обучения. Так, обучение по учебникам алгебры 7, 8 классов Ш. А. Алимова и др. сопровождается пооперационными правилами выполнения алгебраических действий [4, 5]. Существенным недостатком является то, что правила формулируются в "свернутом" виде, то есть не обеспечивают полную пошаговую программу действия, что снижает их применимость, а некоторые не несут никакой информационной и облегчающей нагрузки, например, в правиле вынесения общего множителя за скобку всего два пункта: 1) найти общий множитель; 2) вынести его за скобки. Чтобы учащийся мог применить такой алгоритм к решению конкретной задачи, он должен уметь его развернуть в пошаговую программу действий или вычленить алгоритм из формулы, правила, теоремы, определения с последующим его развертыванием. Это требует значительных умственных и практических усилий, зависящих от объективных условий обучения и субъективных качеств учащихся. Кроме того, применяемые правила, алгоритмы, типовые решения и т.п. составляются без учета психологических закономерностей восприятия и освоения знаний, служат лишь посредником для запоминания, и то в том случае, если не слишком "свернуты". Приобретение навыков происходит за счет заучивания правил и выполнения значительного объема упражнений и задач до тех пор, пока в сознании не отложится пошаговая система операций и действий, что происходит не у каждого учащегося и требует значительных усилий как со стороны преподавателя, так и со стороны учащегося.
Известно средство для нетрадиционного способа обучения, представляющее собой планшет, лицевая сторона которого имеет непрозрачную часть с прозрачной частью вверху, выполненной в виде окна, при этом в прозрачной части, с правой стороны планшета, выполнена прямоугольная выемка до нижнего края окна. В планшет вставляются вкладыши, каждый из которых содержит фиксированные элементы в виде вопросов, по которым ведется выполнение заданий, и правильных ответов, скрытых от учащихся [6]. Однако известное средство предназначено только для опроса и контроля знаний учащихся и не предназначено для проведения на его базе тренировочных упражнений. Данное средство может применяться на конечном этапе обучения, когда учащиеся, обладая некоторыми знаниями, закрепляют их или проверяют. Применяя такое средство для обучения, невозможно приобрести практические навыки решения тех или иных задач непосредственно через осмысление хода операций их выполнения.
Задача, на решение которой направлено изобретение, заключается в значительном повышении эффективности обучения математике в школе, для приобретения практических навыков непосредственно через осмысление хода операций, порядка действий и умозаключений при изучении определенных действий и способов решения задач, а также направлено на развитие алгоритмических, логических и аналитических способностей учащихся, на снижение зависимости уровня обучения от его качества и способностей учащихся.
При решении данной задачи достигается технический результат, заключающийся в переходе от теории (осмысления) к практике без заучивания, с меньшим количеством выполняемых упражнений, с более прочными знаниями, чем при обычных способах обучения.
Указанный технический результат достигается за счет применения в процессе обучения заявленной конструкции средства для обучения, которое представляет собой тренажер для систематического тренинга учащихся и состоит из наполовину прозрачного планшета и комплекта вкладышей по каждой изучаемой теме. На лицевой стороне планшета имеются окошко в верхней левой непрозрачной части и прямоугольная выемка в правой прозрачной части от верха планшета до нижнего края окошка. Комплекты вкладышей формируются по изучаемой теме. Каждый вкладыш в зависимости от стадии обучения содержит фиксированные элементы, по которым ведут выполнение заданных примеров. Фиксированные элементы представляют либо пункты "Алгоритмов действия" или "Алгоритмов поиска решения"; либо задания, упражнения, примеры для отработки алгоритмов и/или приобретения навыков их применения. "Алгоритмы действия" определяют пошаговый порядок операций при выполнении стандартных математических действий. "Алгоритмы поиска решения" определяют порядок действий при поиске способа решения тех или иных задач. Пункты алгоритмов фиксируются на вкладышах слева для "высвечивания" в окошке каждого пункта в отдельности. Задания, упражнения, примеры для отработки алгоритмов и/или приобретения навыков их применения фиксируются справа, если необходимы текстовые выводы при аналитической деятельности, и слева, если необходимо выполнение математических операций и действий для достижения необходимых при освоении умозаключений. Вкладыши представляют собой разделенные по центру листы, разлинованные по размеру окошка. Вкладыши вставляются в тренажер и служат для записи через выемку или окошко выполнения заданных примеров по соответствующим фиксированным элементам: пунктам алгоритмов, фиксируемых на вкладышах слева для "высвечивания" в окошке каждого пункта в отдельности; упражнений, примеров, фиксируемых справа, если необходимы текстовые выводы, и слева, если необходимо выполнение математических операций и действий.
Для получения практических навыков выполнения стандартных базовых действий используются вкладыши с "Алгоритмами действия". "Алгоритмы действия" содержат пошаговую программу изучаемого действия, составленную с учетом психологических закономерностей восприятия и воспроизводства математических знаний, например: "Сложение дробей с разными знаменателями" или "Решение дробных рациональных уравнений" и т. п. Структурно "Алгоритмы действия" представляют пункты пошаговых операций, содержание и последовательность которых разработаны в соответствии с математической теорией и практикой, математической логикой, логикой мышления, на основе анализа и учета ошибок, связанных с неправильным порядком действий и неправильными ассоциациями и умозаключениями. Кроме пунктов математической теории и практики рассматриваемого действия, как в известных алгоритмах, "Алгоритмы действия" включают последовательность записи знаков и символов. Установлено, что акцентирование внимания на этих пунктах создает предпосылки для восприятия и воспроизводства алгоритма в целом. Поэтому во многих алгоритмах такие пункты становятся ключевыми акцентами всего алгоритма. Например: в алгоритме "Вынесение общего множителя за скобку" имеется пункт "Пишем общий множитель и открываем скобку", который после специального тренинга становится ключевым акцентом и подсознательно приводит учащихся к выполнению последующих операций: "В скобках записываем результат деления каждого слагаемого на общий множитель", вырабатывая умение и навык вынесения общего множителя как обобщенного математического действия.
Для получения навыков решения задач, где требуется применять те или иные математические действия, для поиска способов решения стандартных или нестандартных задач используются вкладыши с "Алгоритмами поиска решения".
"Алгоритмы поиска решения" определяют порядок действий при поиске способа решения тех или иных задач, строятся на последовательности действий и умозаключений, составленной в соответствии с принципами логического и аналитического мышления, логикой поиска и выполнения математических действий. Структурно представляют перечень последовательных действий и умозаключений, при выполнении которых задача приводится либо к определенному изученному стандартизированному виду, либо к программе ее решения. Например: "Общий алгоритм решения тригонометрических уравнений", "Алгоритм решения задач табличным способом", "Общий алгоритм решения логарифмических уравнений", "Общий алгоритм решения алгебраических уравнений" и т.д.
Работа с вкладышами, содержащими алгоритмы, обеспечивает оптимальную организацию мыслительного процесса за счет систематизации и последовательности операций поиска и решения, формируют у учащихся мышление логико-математическими структурами и обеспечивают более быстрое и глубокое усвоение материала большим количеством учащихся, чем при традиционных способах обучения, основанных на изучении типовых видов задач и способов их решения.
В заявленном способе обучения учащихся алгебре и началам анализа приобретение практических навыков, навыков аналитической деятельности ведут при помощи тренажера и на его базе осуществляют тренинг учащихся, в процессе которого вкладыш вставляют в планшет для записи выполнения заданных примеров по фиксированным элементам и продвигают вкладыш вверх на одну строку после выполнения очередного пункта, упражнения. Учащиеся устанавливают соответствующие вкладыши и записывают выполняемые операции через окошко по фиксируемым элементам справа, если необходимы текстовые выводы, и через выемку по фиксируемым элементам слева, если необходимо выполнение математических операций и действий. После выполнения операции продвигают вкладыш вверх, выполняя таким образом все задания вкладыша.
Комплекты вкладышей формируются по каждой теме в соответствии со стадиями изучения темы, а фиксированные элементы пунктов алгоритмов составлены с учетом психологических закономерностей восприятия и воспроизводства знаний и содержат акценты, являющиеся ключом для воспроизводства всего алгоритма.
Планшет сконструирован таким образом, чтобы максимально обеспечить условия для лучшего освоения изучаемого материала.
Окошко в левой непрозрачной части планшета предназначено для "высвечивания" одного пункта алгоритма, зафиксированного в каждой строчке на вкладыше слева, обеспечивая тем самым концентрацию внимания только на одном конкретном пункте, или используется для записи выводов и умозаключений при выполнении заданий, упражнений по фиксированным элементам вкладышей, используемых при освоении, отработке алгоритмов, аналитической деятельности, например, при составлении алгоритма самими учащимися или для записи необходимых текстовых аналитических выводов.
Выемка, расположенная в прозрачной части, предназначена для свободной записи выполняемых математических операций по "высвеченному" пункту алгоритма или для записи выполняемых заданий по фиксированным на вкладышах элементам.
Использование окна для записи текстовых выводов, а выемки для записи выполнения математических операций, т.е. слева направо, облегчает процесс осмысления операций и способствует их запоминаю.
Прозрачность правой части тренажера позволяет осмысливать как выполненные операции, так и всю программу действий, что в значительной мере способствует запоминаю без заучивания.
После выполнения одного пункта или упражнения вкладыш продвигают вверх на один шаг и выполняют следующий пункт или упражнение.
Тренажер позволяет проводить данные операции многократно, до тех пор, пока учащийся не осмыслит алгоритм и не приобретет навык выполнения изучаемого действия, обеспечивая возможность проведения уровневого обучения. При этом возникает мотивация к изучению, так как учащийся как бы сам себя обучает и психологически настраивает себя на то, что у него все получится. Кроме этого происходит концентрация внимания на каждой выполняемой операции, "высвечиваемой" в данный момент, что приводит к более глубокому осмыслению и быстрому запоминанию порядка выполнения изучаемого действия без заучивания. Такой процесс обучения позволяет перейти от заучивания к осмыслению и запоминанию, что существенно сокращает время изучения, в меньшей степени зависит от качества преподавания, приучая учащихся к самостоятельности, и как следствие обеспечивает мотивацию к обучению.
По мере проведения тренинга происходит формирование ключевых акцентов алгоритмов, что приводит к его "свертыванию" и автоматическому выполнению действий.
Система тренинга обеспечивает неразрывность процесса получения теоретических знаний и практических навыков. Одной из основных задач тренинга является обеспечение такой формы обучения, при которой знания и навыки приобретаются осмысленно без заучивания и с меньшим количеством тренировочных упражнений. Это достигается за счет максимальной алгоритмизации обучения по всему курсу алгебры и систематическом тренинге на тренажере.
Заявленное средство обучения представлено на фиг.1-2.
На фиг.1 изображен планшет.
На фиг.2 изображен вкладыш с фиксированными элементами.
Планшет 5 разделен на левую непрозрачную часть 1, правую прозрачную часть 4. Лицевая часть планшета имеет окошко 2; выемку 3. Вкладыш 6 представляет собой разделенный по центру разлинованный по размеру окошка лист. Фиксированные элементы 7 по отработке алгоритма располагаются слева по пунктам в каждой строчке вкладыша.
Обучение по заявленному тренажеру ведется следующим образом. Вкладыш 6 с зафиксированными слева пунктами алгоритма 7 учащиеся вставляют в планшет 5 и сверху через выемку 3 записывают заданный пример для выполнения. В окошке 2 "высвечен" пункт 1 алгоритма, выполнение которого учащиеся записывают через выемку в соответствующей строке. Продвигая вкладыш вверх на одну строку, переходят к следующему пункту, записывают его выполнение и проходят таким образом весь алгоритм.
По заявляемому способу были обучены многие учащиеся. Практически все учащиеся отмечали облегчение в освоении материала, многие констатировали, что алгоритмизация как форма мышления помогает им не только в обучении, но и в решении многих жизненных задач. За счет обеспечения максимальной концентрации внимания как на выполнении отдельных пошаговых операций, так и действий в целом учащиеся быстрее осваивают изучаемый материал. Установлено значительное снижение количества ошибок. Приобретаемые навыки становятся более прочными. Уровень положительной мотивации на обучение достигает практически 100 процентов за счет возможности более глубокого осмысления на начальном этапе и формирования на этой основе психологии человека, способного к обучению. Кроме этого, у многих учащихся наблюдалось развитие математических способностей, развитие логического мышления и интеллекта в целом. Учащиеся использовали тренажер и для обучения по другим предметам, например русскому языку, физике, химии, английскому языку и другим, самостоятельно составляя фиксированные элементы вкладышей и проводя тренинг. Отмечено, что тренажер облегчает запоминание, например, при заучивании слов иностранного языка, элементов периодической системы и других перечней.
Источники информации
1. А.В. Гладский. О методической системе В.Ф. Шаталова, журнал "Математика в школе", 4, 1988, стр. 38-42.
2. Н.А. Кудрюмова. О методических подходах к записи учебного материала, журнал "Математика в школе", 3, 1983, стр. 25-30.
3. Патент RU 2120140, кл. G 09 B 23/06, от 10.10.1998.
4. Ш.А. Алимов и др. Алгебра. Учебник для 7 кл. сред. шк., 1993г.
5. Ш.А. Алимов и др. Алгебра. Учебник для 8 кл. сред. шк., 1991г.
6. Патент US 3105307, кл. G 09 B 3/00, от 01.10.1963.

Изобретение относится к средству и способу обучения, а именно обучению математике в школе. Средство представляет собой тренажер, состоящий из наполовину прозрачного планшета, на лицевой стороне которого имеются окошко в верхней левой непрозрачной части и прямоугольная выемка в правой прозрачной части от верха планшета до нижнего края окошка, и комплектов вкладышей. Комплекты вкладышей формируются по каждой изучаемой теме, каждый вкладыш которого представляет собой разделенный по центру лист, разлинованный по размеру окошка, содержащий в зависимости от стадии обучения фиксированные элементы, по которым ведется выполнение заданных примеров и представляющих собой пункты алгоритмов действия, определяющих порядок операций при выполнении стандартных математических действий и алгоритмов поиска решения, определяющих порядок действий при поиске способа решения тех или иных задач, которые фиксируются на вкладышах слева для "высвечивания" в окошке каждого пункта в отдельности; либо упражнения, примеры, для отработки алгоритмов и/или приобретения навыков их применения, которые фиксируются справа или слева. Также описан способ обучения алгебре и началам анализа с применением указанного средства и проведением на его базе тренинга. Данное изобретение позволяет осуществлять переход от теории к практике без заучивания, с меньшим количеством выполняемых упражнений, с более прочными знаниями, чем при обычных способах обучения. 2 с. и 2 з.п. ф-лы, 2 ил.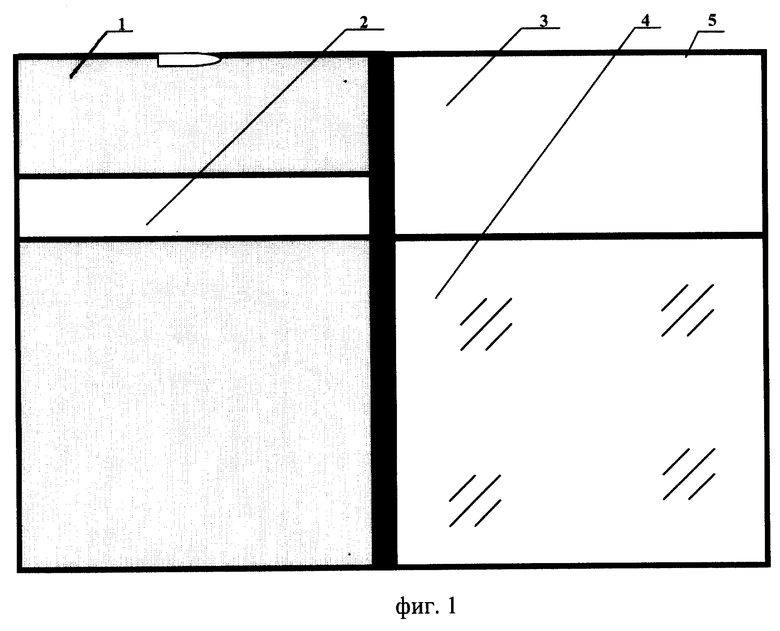
| АЛИМОВ Ш.А | |||
| и др | |||
| Алгебра, Учебник для 7 класса средней школы, 1993 | |||
| ГУСЕВ В | |||
| А., МОРДКОВИЧ А | |||
| Г | |||
| Математика, справочные материалы | |||
| - М.: Просвещение, 1988, с.115, 141 | |||
| US 3105307 А, 01.10.1963. |
Авторы
Даты
2002-05-10—Публикация
2001-02-20—Подача